结构形式对桥墩局部冲刷三维性态发展的影响

熊 文 汪吉豪 叶见曙

(东南大学交通学院，南京 210096)

结构形式对桥墩局部冲刷三维性态发展的影响

熊 文 汪吉豪 叶见曙

(东南大学交通学院，南京 210096)

摘 要:选用基于动网格自更新技术的三维CFD冲刷模型，可以解决既有一维、二维计算研究方法的局限性以及准确性问题，对桥墩冲刷以及周边流场三维性态进行全过程动态跟踪分析.首先采用经典B.W.Melville实验环境以及实验数据，分别从流场、流速以及冲刷坑进行冲刷模型的准确性验证.进而利用该数值模型分别对3种典型桥墩(单柱墩、双柱墩、排墩)周边河床的冲刷深度、冲刷坑形态以及冲刷影响区域进行数值分析，通过数据分析得出各自完全不同的冲刷发展趋势与性态特征.通过对比分析可以看出，桥墩结构形式对桥墩局部冲刷三维性态发展有着显著影响，区分桥墩结构形式对桥墩冲刷设计、理论分析以及长期监测方案设置具有相当的必要性与重要性.

关键词:桥墩结构;局部冲刷;冲刷深度;冲刷坑形态;冲刷影响区域

基础结构的冲刷病害是当今桥梁结构功能失效、丧失其安全性能的最主要原因之一.以美国为例，从1966年至2005年，全美倒塌桥梁(1 502座)中58%的破坏桥梁与桥梁基础结构的冲刷病害有关，美国交通部已将桥梁基础冲刷看作是高速公路桥梁结构功能及安全性能失效的最常见原因之一［1-3］.据美国交通安全委员会统计，每年用于修复及弥补遭受基础冲刷病害桥梁的费用平均高达3 000 美元［2］.

事实上，冲刷模型实验是较为常见的局部冲刷预测方法，且桥墩几何形态与实际能够最大限度保持一致，但实验人力物力花费较高，无法广泛应用于一般中小跨桥梁设计，而冲刷却往往发生在这些普通跨径桥梁之中.另外，规范建议的冲刷深度计算公式逐渐成为桥梁基础冲刷深度预测的主要理论依据，该方法简单实用，可快速对桥梁基础冲刷病害进行预判.但是计算假设条件苛刻，参数单一，计算结果难以保证准确，更无法给出冲刷三维性态发展趋势［4］.所以，现阶段桥梁设计一般仅以简化为一维的冲刷深度为设计条件来进行基础设计［4］.

但是，冲刷并不是一个简单的一维事件，它是一个随时间不断变化的实时复杂三维事件.显然，在桥梁设计中，不仅冲刷深度是关键设计参数，冲刷三维性态的发展趋势，包括最深冲刷深度所对应的平面位置，更是与桥梁基础结构力学性能、耐久性能息息相关的影响因素.近年来，国内外学者针对桥墩冲刷三维性态发展开展了一系列研究，但研究多以单圆柱(墩)冲刷为研究对象，因而研究成果不能完全应用于实际桥梁基础结构设计中［1-3，5］.

本文针对以上问题，选用基于动网格自更新技术的三维CFD冲刷模型，对3种典型桥墩结构形式(单柱墩、双柱墩、排墩)及桥墩冲刷三维性态发展进行数值跟踪.参照经典B.W.Melville实验环境［6］，分别对3种典型桥墩周边河床的冲刷深度、冲刷坑形态、冲刷影响区域进行数值分析，得出各自的发展趋势与性态特征，通过对比结构形式对局部冲刷三维性态发展的影响，说明区分桥墩结构形式对冲刷分析的必要性与重要性.研究成果可对桥墩选型、冲刷监控方案设计以及更复杂的冲刷理论计算公式建立理论基础及提供理论依据.

1 三维CFD冲刷模型

1.1 流场模型建立

本研究中三维CFD冲刷模型将基于B.W.Melville经典冲刷试验，采用CFD流体动力学有限元计算软件Fluent(ANSYS)进行建模.B.W.Melville试验水槽长19 m，宽45.6 cm，在水槽中放置直径为5.08 cm的圆柱作为桥墩模型，圆柱形桥墩中心距水槽两侧的距离为22.8 cm，床底泥沙平均粒径d50为0.385 cm，水流平均速度为 0.25 m/s，床面倾角为 1/10 000(见图 1)［6］.

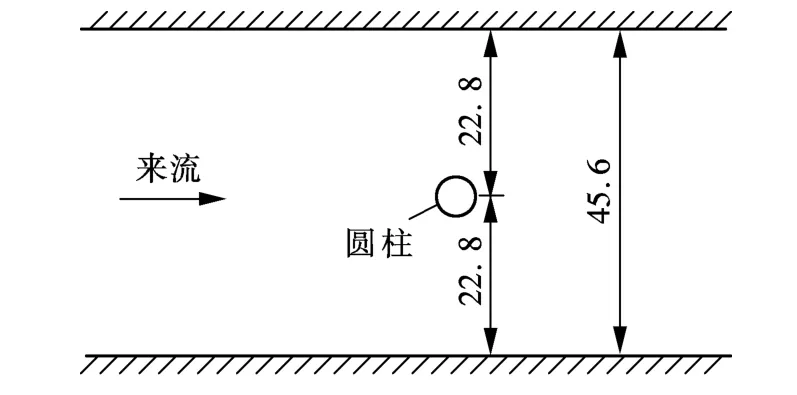
图1 B.W.Melville试验模型(单位:cm)

根据 Sarker［7］的研究结论，圆柱下游 12 倍直径距离以外流动不受圆柱的影响.故本次研究为节省计算时间，基于B.W.Melville试验数据，三维CFD冲刷数值模型总长度选为20d(d为圆柱桥墩直径，20d=101.6 cm)，桥墩中心距下游出流距离为14d，满足大于12d的要求，桥墩中心距上游进口距离为6d，计算宽度为45.6 cm，高度为15 cm.

虽然六面体结构化网格计算效率和计算精度均较高，但与四面体非结构化网格相比，四面体的非结构化网格的适应性以及网格的变形能力均较强［8］.特别是对于局部冲刷，这种局部变形非常剧烈，且变形不规则，采用六面体结构化网格很难适应变形的需要.故本研究采用四面体非结构化网格进行流场网格划分，同时在桥墩附近以及流场底部加密网格以满足桥墩附近及河床处复杂水流结构的计算要求.

由于是瞬态问题，必须提供流场的初始条件.此处主要是指流场速度进口的初始条件，可通过选取与计算模型尺度相同的长方体模型来获得，而流出边界采用自由出流边界条件.为了获得速度分布，本研究选取与数值模型尺度相同的长方体模型来获得进口的速度分布，如图2所示.

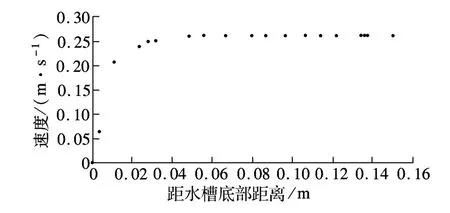
图2 进口速度分布图

不同桥墩结构形式的流场模型如图3所示.在这3个模型中，除桥墩条件不同外，其他条件均相同.其中，单柱墩模型桥墩直径d=5.08 cm(见图3(a)、(b));双柱墩模型的两桥墩中心距离取为3d，两桥墩中心连线的中点位于B.W.Melville试验桥墩的中心位置(见图3(c));排墩模型长度为3d(有圆角)，宽度为d，排墩中心与B.W.Melville试验桥墩的中心位置相同(见图3(d)).

图3 不同桥墩结构形式的流场

1.2 局部冲刷模拟

本次研究将直接对CFD流体动力学有限元计算软件Fluent进行二次开发，采用动网格自更新技术模拟桥墩局部冲刷过程，准确精细地控制底部动边界网格每一个节点的实时运动，更加真实地还原实际局部冲刷的发展过程.

动网格自更新技术需要用到Fluent中的UDF功能，使用UDF编译型(compiled)函数求解底部边界冲刷位移量.具体来说，利用DEFINE_GRID_MOTION()宏命令控制底部边界每个节点运动;利用 NV_MAG(F_STORAGE_R_3V(f，t，SV_WALL_SHEAR))/NV_MAG(A)宏命令获取底部边界每个面单元的平均切应力.继而采用泥沙运动方程［9-11］，即

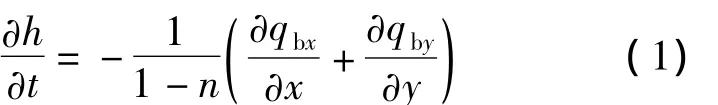
式中，h为河床高程;t为时间变量;n为河床泥沙空隙率，本次研究参考试验资料取为 0.40［12］;qbx，qby分别为沿x，y方向的推移质单宽体积输沙率.通过相关编程语句(工具宏)求解出底部边界每个河床节点的高程(位移)变化量.

求出底部边界每个节点的位移量后，就需要在每个时间子步内对计算域网格进行动态更新，即模拟实际冲刷实时动态过程.本文动边界网格更新策略联合采用弹簧光顺方法(spring based method)和局部网格重画模型(remeshing method).具体来说，弹簧光顺方法是将网格任意2个节点之间视作弹簧连接，当边界发生位移变形时根据网格节点受力为零这一条件，通过迭代计算出整个网格节点的位移量，但此方法不适用于大变形(相对于网格尺寸)情况.为解决这一问题，需要联合采用局部网格重划模型.局部网格重划是监测网格中变形网格的最大、最小网格尺寸以及网格畸变率.一旦网格变形过程中单元网格特性超过设定范围，便自动对网格进行标记重划.经反复试验对比研究，联合使用这2种方法能够保证动网格变形更新准确性的同时兼顾动网格质量，床面底部切应力计算也较为准确，非常适合桥墩局部冲刷的数值模拟.

河床高程的正确计算是动网格进行自更新的关键依据.显然，关键在于对输沙率梯度的准确求解，即首先需要准确判断每一目标面单元的相邻单元，以便进行输沙率梯度的计算.

由于Fluent中循环遍历宏(begin_f_loop(f，tf))循环操作的相邻2个循环步所针对的2个面单元并不一定相邻，故本文利用冒泡排序的思想来寻找最近相邻单元.具体来说，就是在循环遍历到某个单元时，进行循环嵌套，再次循环遍历所有其他面，进而通过坐标距离判断出目标面单元最近的相邻单元，最后通过这两单元信息的差分来求解输沙率梯度.一旦找到最近相邻单元面，即可利用下式:

进行输沙率梯度计算.式中，为输沙率梯度;qi，qi，near为相邻两单元推移质单宽体积输沙率;xi，xi，near为相邻两单元坐标(位置).进而以计算结果进行动边界网格更新，可以看出单元划分精细程度直接与计算精度相关.

2 数值模型验证

为验证本研究建立的冲刷模型的准确性，将其流场、冲刷坑以及冲刷深度的计算结果与B.W.Melville经典试验结果进行对比.由于为单柱墩试验，所以其准确性验证仅针对单柱墩数值模型(见图3(a)、(b))进行.

图4(a)给出距离河床面2 mm的数值流场流速矢量切面图，图4(b)给出取自B.W.Melville试验数据的实际流场距离底部2 mm的流线图.对比图4(a)与图4(b)可以看出，数值模拟结果中桥墩附近存在的水流回流以及漩涡水流均与实际流场结果基本吻合.

图4 流场对比

图5(a)为数值计算得到的30 min桥墩局部冲刷坑形态，图5(b)为 B.W.Melville试验中30 min桥墩局部冲刷坑的地形等高线图.可以看出，大部分区域数值计算地形等高线与试验结果吻合.

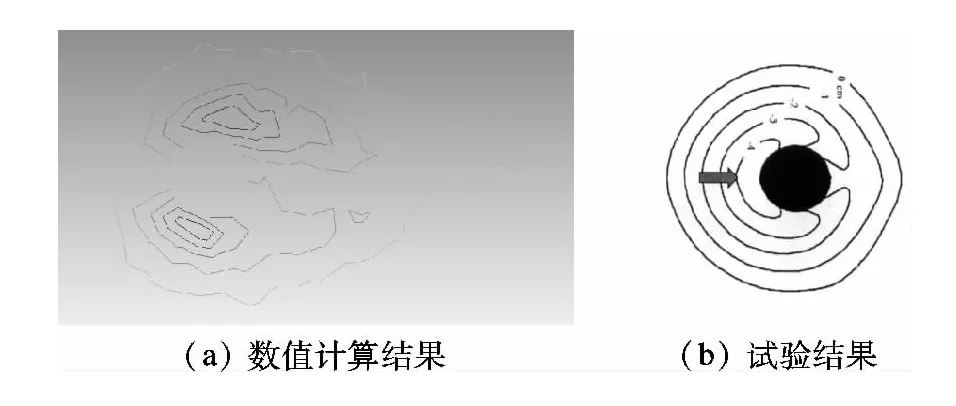
图5 冲刷坑对比

在B.W.Melville试验中，进行到约2.5 h时达到冲刷平衡，此时平衡冲刷深度约为6 cm，其中试验进行到30 min时的冲刷深度为4 cm.由此可见冲刷前30 min发展较为剧烈，冲刷发展也较为充分，而之后冲刷发展开始缓慢.由于计算机硬件限制，本次研究仅对前30 min冲刷发展进行分析，计算得到的前30 min最大冲刷深度为4.4 cm(见图6).与B.W.Melville试验结果相比，同时考虑到泥沙输运理论与实际泥沙输运本身存在的一定差异性，可以认为本次冲刷数值模型对于局部冲刷深度的计算具备可信性.

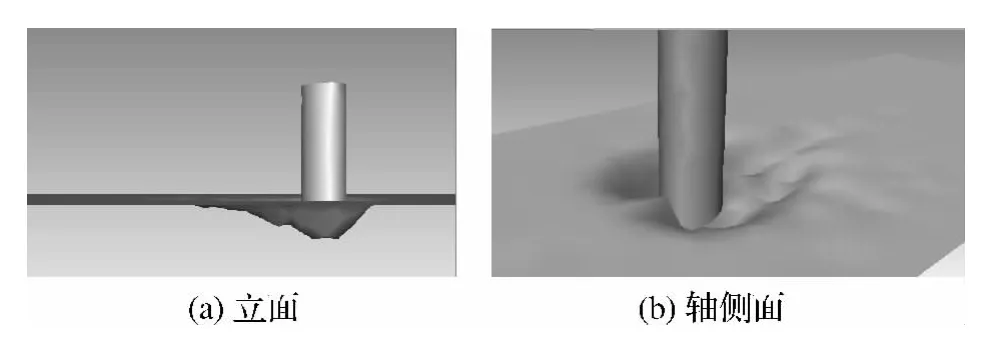
图6 单柱墩模型冲刷深度

综上所述，无论从平面形态还是深度发展，无论从流场还是河床角度，本文建立的计算模型均可以准确地对桥墩周边流场以及局部冲刷进行数值模拟，并得到正确的计算结果.

3 桥墩结构形式影响分析

基于3种桥墩以及流场的数值模型(见图3)，利用准确性经过验证的计算方法，进行桥墩结构形式对局部冲刷三维性态发展的影响研究.

3.1 冲刷深度对比分析

对于单柱墩冲刷模型，前30 min的最大冲刷深度为4.4 cm，最大冲刷深度位置发生在桥墩侧面偏迎水面方向位置(见图6).在整个模拟过程中，前5 min桥墩局部冲刷发展最为剧烈，最大冲刷深度发展较快，在5～25 min冲刷发展的速度较为一致，发展速度居中，25 min以后冲刷开始减缓.事实上，局部冲刷的发展速度是由流场和泥沙2个因素变化共同控制的.在前期，由于最大切应力比临界起动切应力数值大得多，因此前期冲刷发展很快.对于后期由于底部边界的下切，流场运动的空间增大，必定会导致流动的减弱，对于泥沙携带能力的减弱，从而导致冲刷变缓.

对于双柱墩冲刷模型，图7给出了前30 min局部冲刷性态图.图中可以看出双柱墩条件下前后两墩的冲刷深度存在明显差别，后墩冲刷深度明显比前墩要小很多，同时双柱墩条件下不存在明显的沙脊.但是在整个计算时间内，冲刷深度发展趋势和单柱墩相似.

图7 双柱墩模型冲刷深度

图8给出了排墩模型的局部冲刷图.从图中可以看出，对比单柱墩，排墩冲刷深度沿水流方向垂直排墩向后发展不明显，主要沿排墩侧面发展.

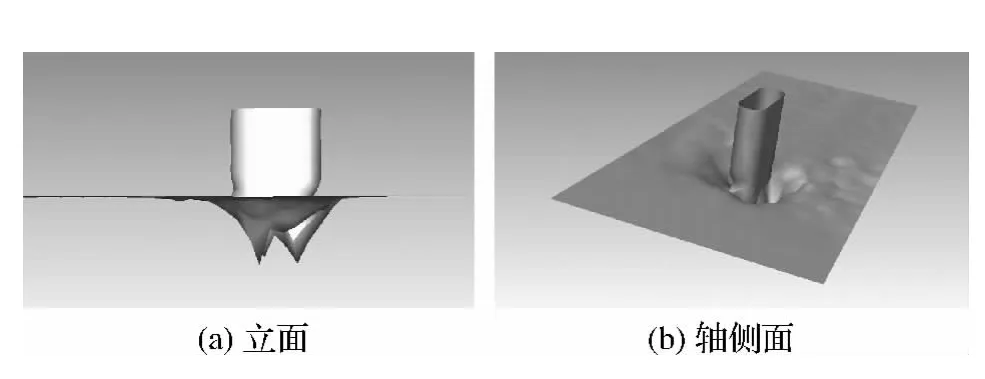
图8 排墩模型冲刷深度

图9 冲刷深度对比

单柱墩、双柱墩以及排墩的整体最大冲刷深度随时间的变化曲线如图9所示.从冲刷深度来看，在同等流场环境(B.W.Melville试验环境)下，排墩的最大冲刷深度最大，双柱墩次之，单柱墩的最大冲刷深度最小.虽然双柱墩的前墩最大冲刷深度较单柱墩有所增加，但后墩的最大冲刷深度减小很多，这主要是由于前墩对水流的阻挡作用使后墩处水流强度减弱.三者均在冲刷初期发展相对较快，后期冲刷深度发展均存在减弱趋势.

另外，从最大冲刷深度位置来看，双柱墩条件下，整体最大冲刷深度位置仍与单柱墩相似;而排墩最大冲刷深度发生在较排墩一侧中心线偏后方向.

3.2 冲刷坑形态对比分析

由于冲刷坑为三维形态，为更精细地观察，在冲刷坑内部进行截面切片(见图10).图11和图12为单柱墩模型30 min冲刷坑形态分析结果，横向为沿水流流向X方向，纵向为沿Y方向，每隔0.25d作截面切片图.

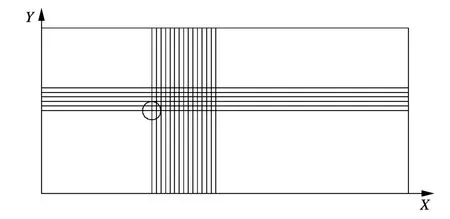
图10 单柱墩模型截面切片位置示意图

图11 单柱墩模型X方向冲刷坑截面切片图

图12 单柱墩模型Y方向冲刷坑截面切片图

从图11和图12可以看出，对于单柱墩模型，桥墩局部冲刷在桥墩垂直水流方向(Y方向)1.5d位置处，冲刷发展已经不明显.而桥墩后方存在较长的沙脊，局部冲刷在桥墩后的影响范围较大.

图13为双柱墩模型截面切片位置示意图.图14和图15为双柱墩模型30 min冲刷坑形态分析结果.

图14 双柱墩模型X方向冲刷坑截面切片图

图15 双柱墩模型Y方向冲刷坑截面切片图

从图14和图15可以看出，对于双柱墩模型，沿水流方向距离第2个(后)墩中心1.75d处冲刷发展已不明显，而桥墩迎水流正方向的局部冲刷影响范围在距离第1个(前)墩外侧1.0d处.

图16为排墩模型截面切片位置示意图.图17和图18为排墩模型30 min冲刷坑形态分析结果.

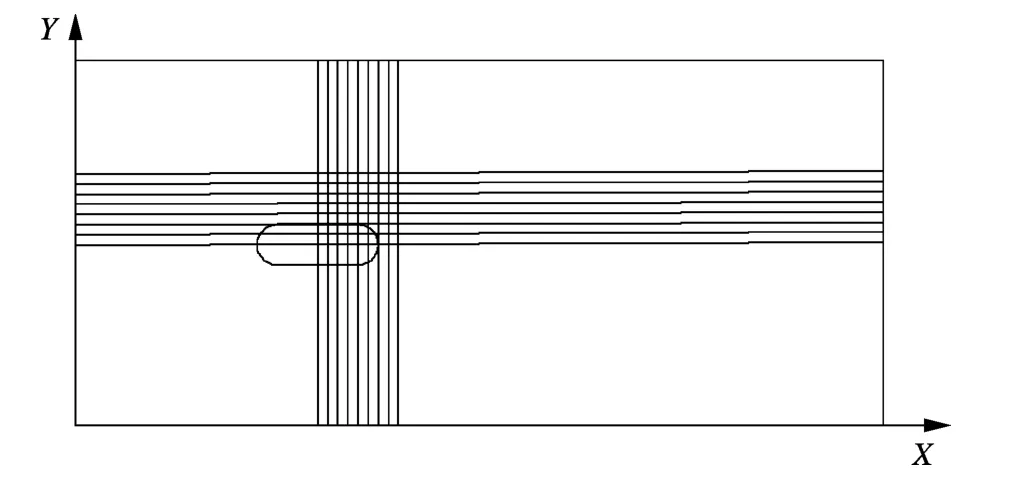
图16 排墩模型截面切片位置示意图

图17 排墩X方向冲刷坑截面切片图

图18 排墩Y方向冲刷坑截面切片图

从图中可以看出，排墩条件下，沿水流方向距离排墩中心2d距离处冲刷发展已经不明显，说明沿水流方向局部冲刷的影响范围为距离排墩外侧0.5d.排墩条件下，排墩迎水流正前方的局部冲刷发展并不明显.

综上可以看出，3种桥墩结构形式对冲刷三维形态发展有显著影响.

3.3 冲刷影响范围对比

基于3.2节对冲刷形态的分析结果，可以分别得出3种桥墩结构形式下，30 min桥墩局部冲刷的影响区域(见图19).桥墩周围的局部冲刷影响区域具有重要意义，它为以后局部冲刷前处理加密网格指出了方向以及加密的具体范围，也为实际桥梁冲刷深度监测范围提供了理论参考依据.可以看出，不同桥墩形式对局部冲刷影响区域的影响非常明显，因此，必须针对不同桥墩形式分别进行考虑.

通过以上对比分析，可以看出桥墩结构形式对局部冲刷分析结果会产生显著影响，不同的桥墩结构形式会导致冲刷性态三维发展相异，如简单将某一种桥墩形式的冲刷分析结论直接应用到其他桥墩形式上，会产生较大误差，结果将明显不可信.

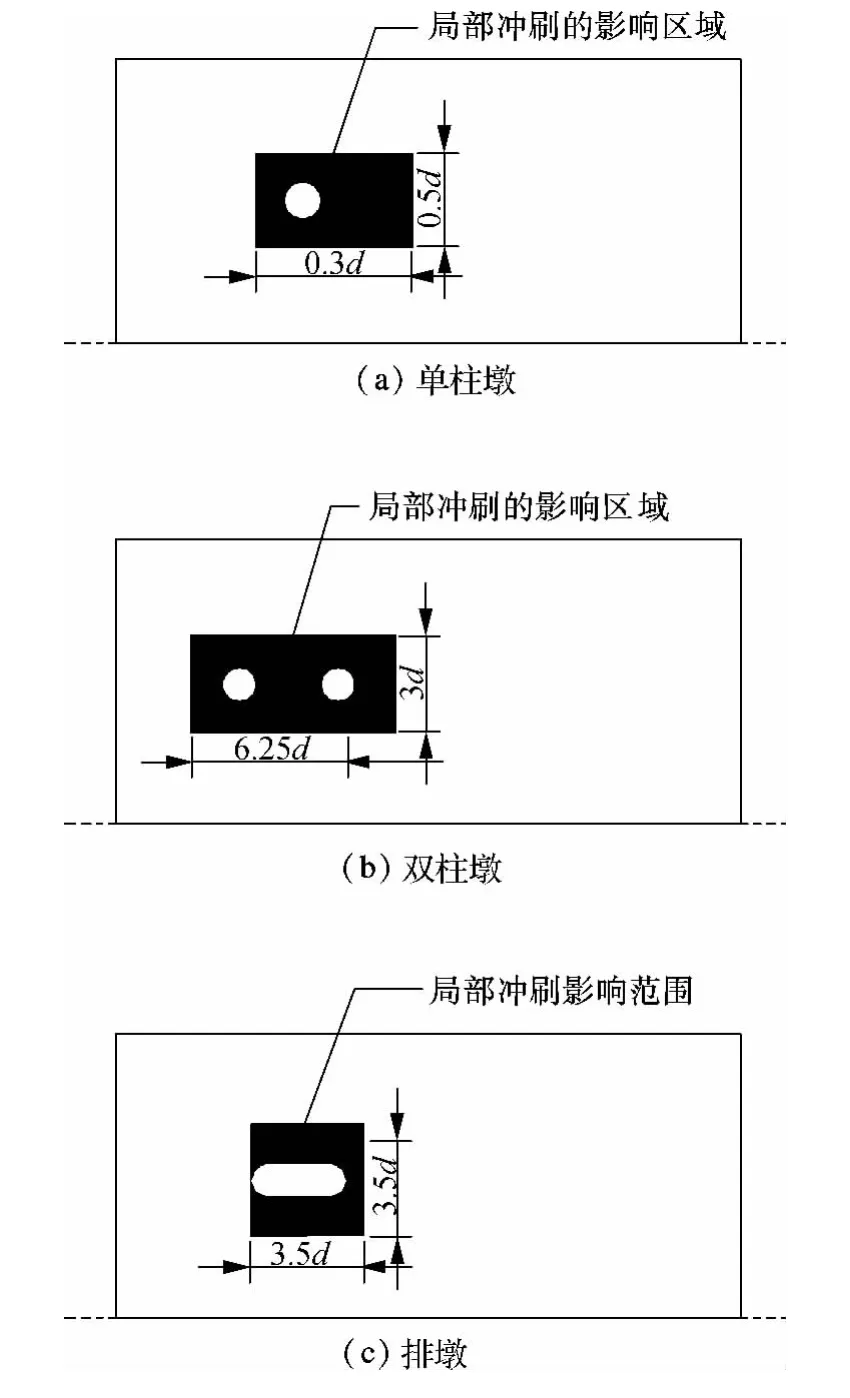
图19 30 min局部冲刷影响区域

4 结论

1)从最大冲刷深度来看，排墩最大，双柱墩次之，单柱墩最小;从最大冲刷深度位置来看，双柱墩整体最大冲刷深度位置与单柱墩相似，而排墩最大冲刷深度发生在排墩一侧较排墩中心线偏后方向.

2)3 种桥墩结构形式无论对垂直还是平行于纵桥向的冲刷坑形态发展均有显著影响.

3)3 种桥墩结构形式有着完全不同的局部冲刷影响区域.该区域为局部冲刷前处理加密网格指出了方向以及加密的具体范围，也为实际桥梁冲刷深度监测范围提供了理论参考依据，必须针对不同桥墩形式分别进行考虑.

本研究成果可对桥墩选型、冲刷监控方案设计以及更复杂的冲刷理论计算公式建立理论基础及提供理论依据.但由于泥沙运动的不确定性，现阶段泥沙输运模型与实际仍存在差异，未来将探索随机运动理论在冲刷计算中的应用，进而采用更加符合实际情况的泥沙输运模型来提高冲刷数值计算的准确性.另外，将桥墩结构形式参数化，进而对桥墩设计参数进行更为系统的局部冲刷参数分析，以期得到更为普遍性的结论.同时河床物理参数对桥墩冲刷的影响研究也正在进行中，包括冲刷防护措施(scour countermeasure)的设计理论.

［1］Kattell J，Eriksson M.Bridge scour evaluation:screening，analysis，and countermeasures［M］.San Dimas，CA，USA:USDA Forest Service，1998:1-12.

［2］Hunt E B.Monitoring scour critical bridges［M］.Washington， DC， USA:Transportation Research Board，2009:1-10.

［3］Deng L，Cai C S.Applications of fiber optic sensors in civil engineering［J］.Structural Engineering＆Mechanics，2007，25(5):577-596.

［4］中交公路规划设计院.JTGD60—2004公路桥涵设计通用规范［S］.北京:人民交通出版社，2004.

［5］郭辉，齐梅兰.跨河桥梁压缩冲刷数值模拟研究［J］.中国铁道科学，2011，32(5):43-49.

Guo Hui，Qi Meilan.Numerical simulation study on the contraction scour of bridge cross the river［J］.China Railway Science，2011，32(5):43-49.(in Chinese)

［6］Melville B M.Local scour at bridge sites［D］.Auckland，New Zealand:School of Engineering，University of Auckland，1975.

［7］Sarker M A.Flow measurement around scoured bridge piers using acoustic-doppler velocimeter(ADV)［J］.Flow Measurement and Instrumentation，1998，9(4):217-227.

［8］Khosronejad A，Kang S，Sotiropoulos F.Experimental and computational investigation of local scour around bridge piers［J］.Advances in Water Resources，2012，37(3):73-85.

［9］赵振兴，何建京.水力学［M］.2版.北京:清华大学出版社，2011:5-35.

［10］钱宁，万兆惠.泥沙运动力学［M］.北京:科学出版社，2003:245-257.

［11］陈小莉.局部绕流冲刷机理及数值模拟研究［D］.北京:清华大学水利水电工程系，2008.

［12］凌建明，林小平，赵鸿铎.圆柱形桥墩附近三维流场及河床局部冲刷分析［J］.同济大学学报:自然科学版，2007，35(5):582-586.

Ling Jianming，Lin Xiaoping，Zhao Hongduo.Analysis of three-dimensional flow field and local scour of riverbed around cylindrical pier［J］.Journal of Tongji University:Natural Science，2007，35(5):582-586.(in Chinese)

Effect of pier structures on local scour 3D developments

Xiong Wen Wang Jihao Ye Jianshu
(School of Transportation，Southeast University，Nanjing 210096，China)

Abstract:In the present study，a three-dimensional(3D)computational fluid dynamics(CFD)numerical model is applied to simulate the local bridge scour based on the dynamic mesh techniques，which solves the limitation and accuracy issues of the existing 1D and 2D methodologies.Using this model，the local scour 3D Development process including the surrounding flow field can be traced in real time.The simulation accuracy is proved by comparing the numerical results to the measuring data in the classic B.W.Melville experiment from the viewpoints of flow field，velocity，and scour hole.After that the scour depth，scour development pattern，and scour influence area are numerically investigated under three different typical pier structures(shapes).By conducting data analysis this simulation gives that different pier structures(shapes)result in totally different local scour results including developing trend and characteristics.It can be concluded that the effects of pier structures(shapes)on local scour 3D development is very obvious，which should be necessary and important in the scour design，analysis and long-term monitoring.

Key words:pier structures(shapes);local scour;scour depth;scour development pattern;scour influence area

中图分类号:U442.5

A

1001－0505(2014)01-0155-07

doi:10.3969/j.issn.1001 －0505.2014.01.028

收稿日期:2013-06-20.

熊文(1982—)，男，博士，讲师，wxiong@seu.edu.cn.

基金项目:国家自然科学基金资助项目(51208097)、高等学校博士学科点专项科研基金资助项目(20120092120058)、江苏省自然科学基金资助项目(BK2012343).

熊文，汪吉豪，叶见曙.结构形式对桥墩局部冲刷三维性态发展的影响［J］.东南大学学报:自然科学版，2014，44(1):155-161.［doi:10.3969/j.issn.1001 －0505.2014.01.028］