单箱多室波形钢腹板箱梁荷载横向分布

马 磊 万 水 蒋正文 李明鸿

(东南大学交通学院，南京 210096)

单箱多室波形钢腹板箱梁荷载横向分布

马 磊 万 水 蒋正文 李明鸿

(东南大学交通学院，南京 210096)

摘 要:将单箱多室波形钢腹板箱梁等效为平面板梁模型，用刚接梁法推导了单箱多室波形钢腹板箱梁荷载横向分布系数的计算公式，并对1根单箱双室波形钢腹板箱梁进行了荷载横向分布试验研究.研究结果表明，刚接梁法计算结果与试验及有限元结果的误差均小于7%，与考虑中横隔板的有限元结果相比，偏于安全.对于有、无中横隔板的单箱多室波形钢腹板箱梁，均可采用刚接梁法计算其荷载横向分布.根据试验结果建议单箱双室波形钢腹板箱梁荷载横向分布系数沿桥跨的取值为:弯矩可统一采用横向分布系数mc(mc为刚接梁法计算的跨中荷载横向分布系数);中梁支反力在梁端采用0.6m0(m0为杠杆原理法计算的梁端荷载横向分布系数)，L/4～L区段内采用mc，梁端至L/4区段，呈直线形过渡;边梁支反力可统一采用0.9m0.

关键词:桥梁工程;单箱多室;波形钢腹板;刚接梁法;荷载横向分布

单箱多室波形钢腹板PC组合箱梁桥［1］具有自重轻、结构造型美观、工期短、抗震性能好等优点，国内外已建成多座此类桥梁.波形钢腹板箱梁设计一般可通过有限元软件建立空间模型，计算波形钢腹板箱梁各构件的内力，但其建模过程复杂，效率低下.

国内外学者针对箱梁的荷载横向分布开展了大量的研究.文献［2-3］针对单箱多室混凝土曲线箱梁桥，提出了刚性截面法及考虑横截面弹性变形的内力横向分配算法.文献［4-5］通过变化桥梁跨度、主梁间距等参数，回归得到内梁的横向分布系数计算公式.文献［6］采用修正的偏心压力法，计算变截面箱形钢-混凝土连续组合梁桥的荷载横向分布系数.文献［7］在刚接梁法基础上，考虑了组合梁与原桥主梁刚度、间距差异，建立修正刚接梁法来计算旧桥加宽后的横向分布系数.文献［8-11］对波形钢腹板梁活载作用下的力学性能进行了研究，但均未涉及单箱多室波形钢腹板箱梁荷载横向分布系数.

本文采用刚接梁法，推导无中横隔板的单箱多室波形钢腹板箱梁荷载横向分布系数的计算公式，并对1根单箱双室波形钢腹板箱梁进行试验研究，以验证刚接梁法的准确性.

1 计算理论

1.1 基本假定

对单箱多室波形钢腹板箱梁横向分布进行分析时，根据其力学特性引入以下基本假定:

1)钢腹板与上、下混凝土板共同工作，不发生相对滑移.

2)纵向弯矩由混凝土顶板和底板承受，不考虑波形钢腹板的纵向抗弯惯矩.

1.2 计算模型

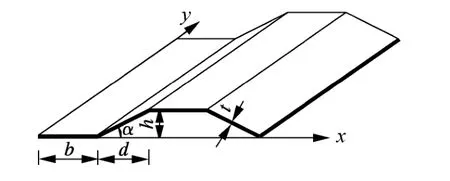
图1 波形钢腹板的波纹形状

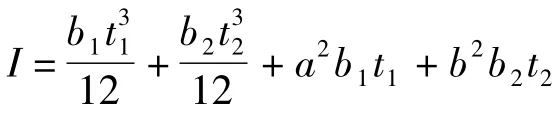
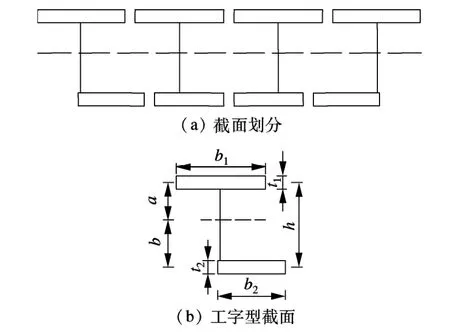
图2 波形钢腹板箱梁截面划分图

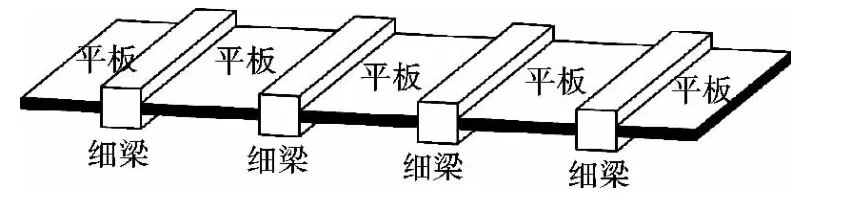
图3 平面板梁模型

1.3 刚接梁法

平面板梁模型切口内存在赘余剪力和赘余弯矩(见图4(a))，取外荷载为单位正弦荷载.根据力法原理，由刚接梁法推导单箱多室波形钢腹板箱梁荷载横向分布的计算公式，建立如下力法方程:

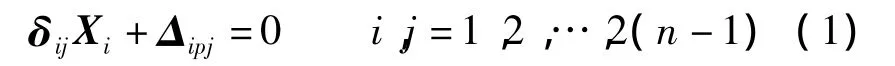
式中，δij为柔度系数矩阵;Xi为赘余竖向剪力和弯矩矩阵;Δipj为荷载引起的位移矩阵.

平面板梁模型中赘余力与变形的关系如图4所示，根据图示可得各柔度系数矩阵中的系数为

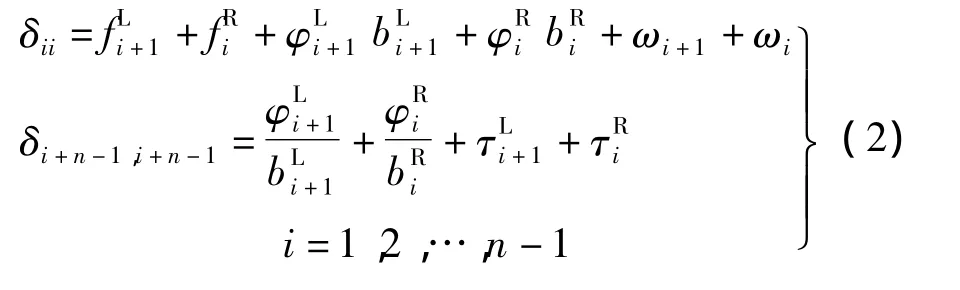
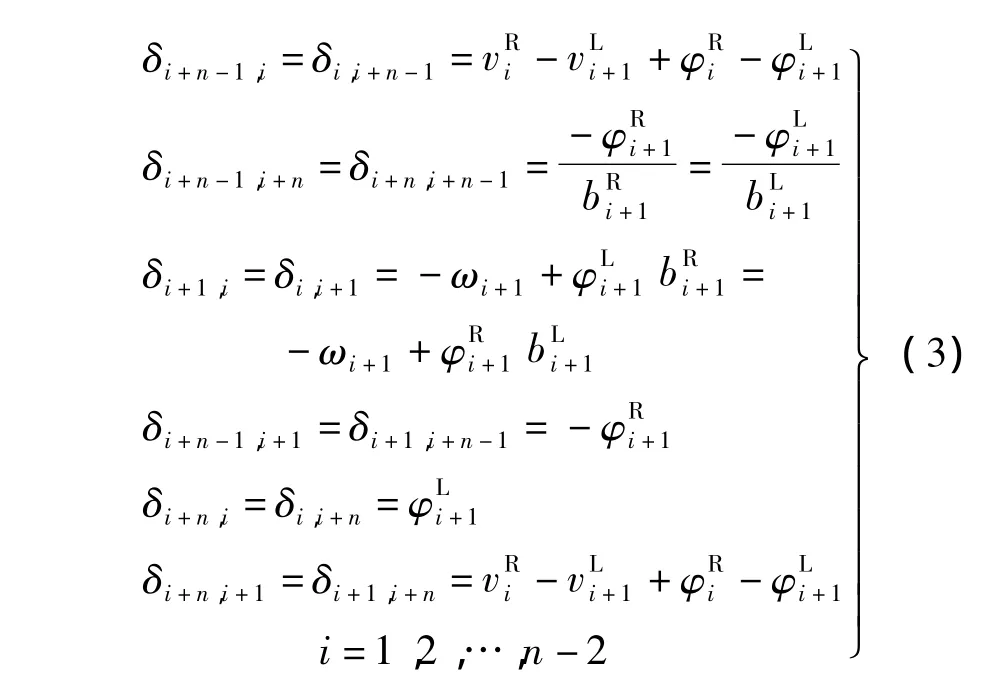
式中，ωi=l4/［π4(EIi)］为单位正弦荷载作用下各细梁的跨中挠度;φki=bkil2/［π2(GIti)］为单位正弦荷载作用下各细梁跨中扭转角;fik=(bik)3/(3EItri)为单位剪力作用下各悬臂板端的挠度;τki=bki/(EItri)为单位力偶作用下各悬臂端的转角;vki=0.5(bki)2/(EItri)为单位剪力作用下各悬臂端的挠度;k=L，R表示梁的左端和右端;EIi为各细梁的抗弯刚度;GIti为各细梁的抗扭刚度;EItri为单位宽度混凝土悬臂板的抗弯刚度;G为混凝土的剪切模量;E为混凝土的弹性模量.

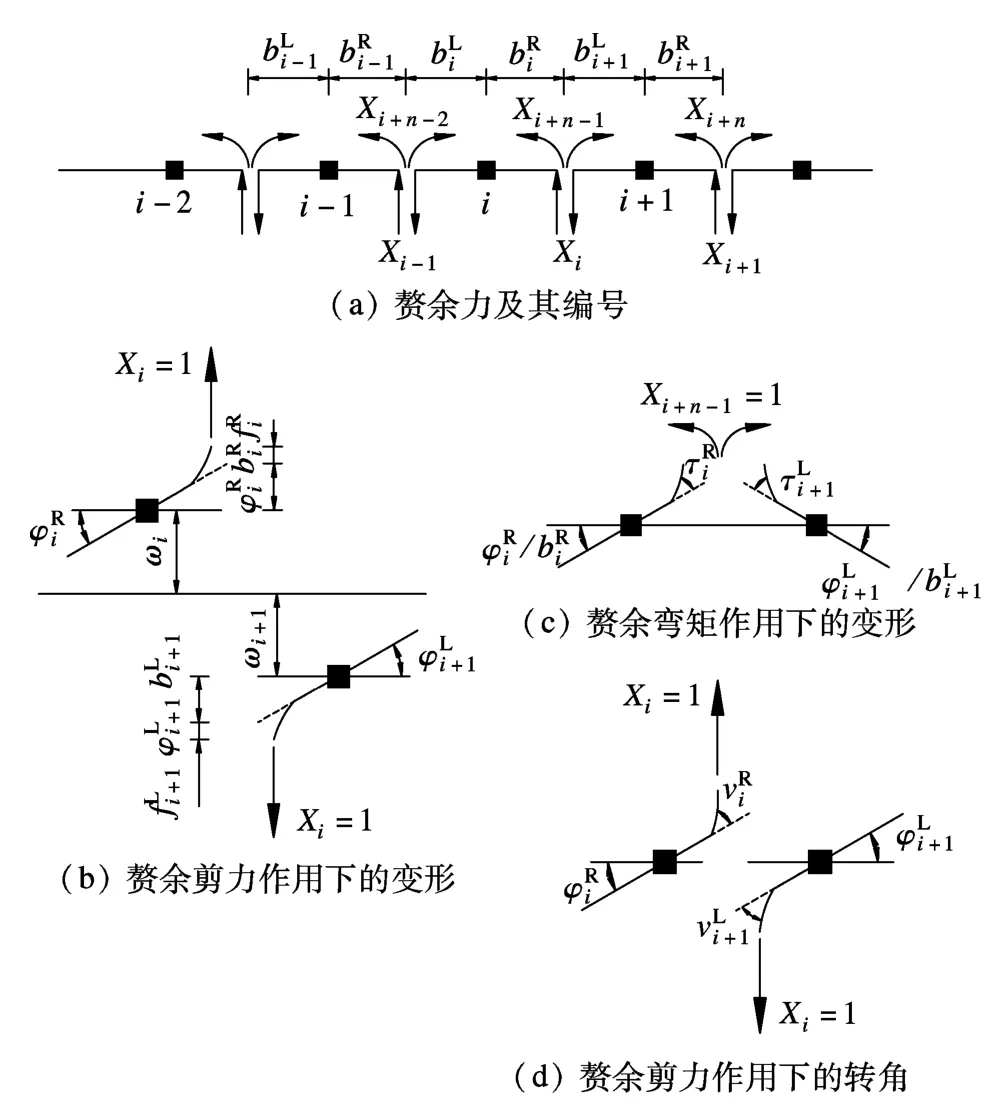
图4 刚接梁法求解示意图

j为外荷载P的作用位置，则有

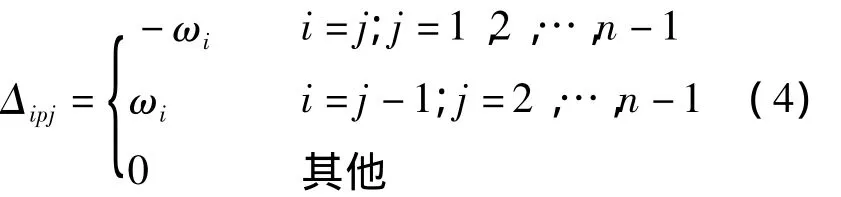
将式(2)～(4)代入式(1)，解出所有赘余力Xi.根据解出的赘余剪力和力的平衡方程可得分配至各主梁的竖向荷载峰值，由此可得各主梁荷载横向分布影响线，进而求得各主梁的荷载横向分布系数.

2 计算理论的验证

为验证上述计算方法的准确性，设计了1根简支单箱双室波形钢腹板箱梁，如图5(a)所示，梁计算跨径为5 m，梁高0.35 m，两侧梁端均设置端横梁.纵向设置2根φs15.24 mm钢绞线，其抗拉标准强度为1 860 MPa，张拉控制应力为1 395 MPa.顶、底板采用 C50混凝土，厚0.05 m，顶板宽1.2 m，底板宽0.9 m.腹板为Q235A波形钢板，波长144 mm，水平面板宽40 mm，折叠角度为36.9°，波高24 mm，厚3 mm.试验梁横截面、钢腹板大样分别见图 5(b)、(c).

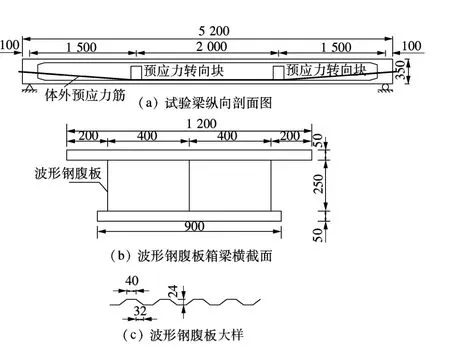
图5 试验梁(单位:mm)

2.1 试验梁理论计算

将试验梁截面换算为混凝土截面并划分为如图6所示的工字型截面梁.划分后的箱梁等效转化为有3根纵向主梁的平面板梁模型，模型的各主梁截面几何特性见表1.计算柔度系数矩阵及位移矩阵中各系数，并代入式(1)，解得各主梁跨中横向分布系数如表2所示.

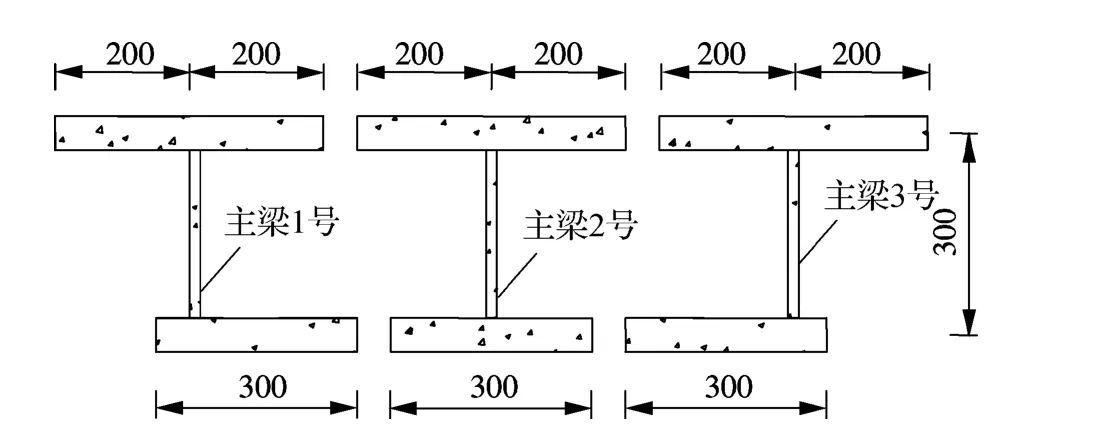
图6 试验梁截面划分(单位:mm)

表1 各主梁截面几何特性 MN·m2

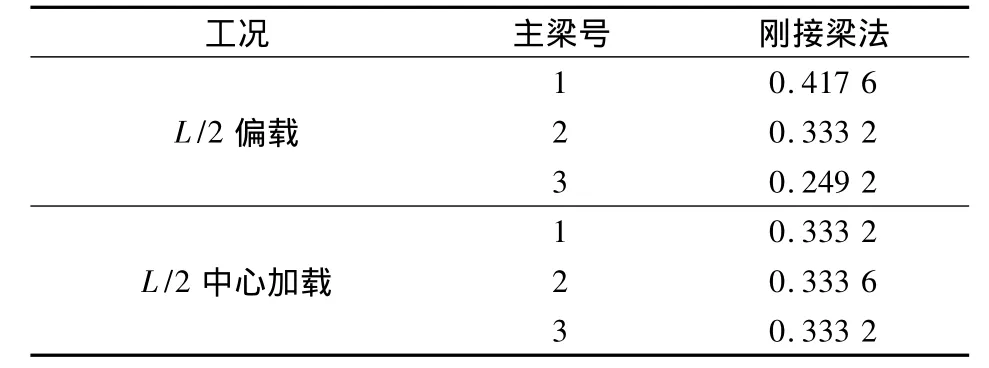
表2 各主梁跨中处横向分布系数

2.2 试验加载和量测方案

采用500 kN油压千斤顶对图5所示的试验梁在端部、L/8、L/4、3L/8和L/2截面处进行单点加载，加载分中心加载、偏载2种工况.在L/2，L/4截面处加载时，分别量测相应截面处各测点的挠度、纵向正应变、端部的支反力.端部、L/8、3L/8截面处加载时量测端部的支反力.各工况加载位置及测点布置如图7所示.

图7 各工况加载位置及测点布置(单位:mm)

2.3 结果对比

利用ANSYS建立试验梁三维有限元模型.混凝土采用 SOLID45单元，波形钢腹板采用SHELL63单元.表3为刚接梁法、试验及有限元的荷载横向分布系数结果对比表.实际工程中通常在跨中设置一道横隔板，用有限元计算跨中无横隔板及有横隔板的荷载横向分布系数.

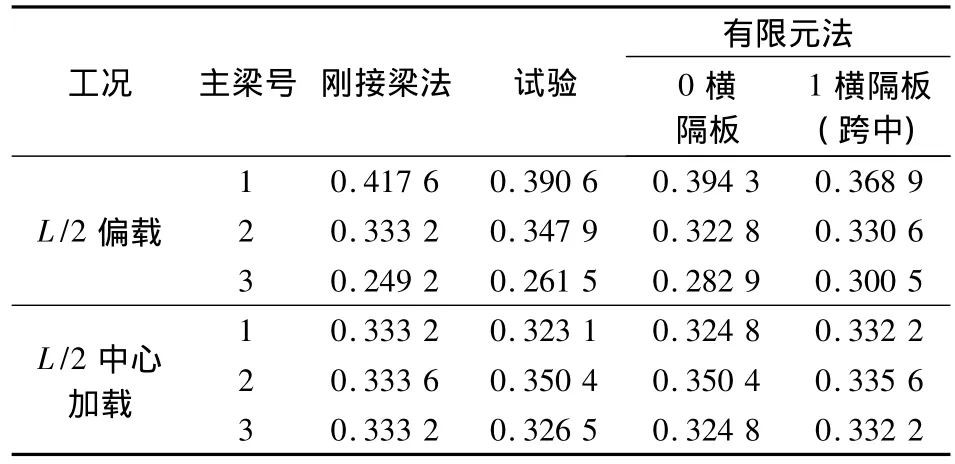
表3 各主梁跨中处横向分布系数

由表3可知，采用刚接梁法计算无中横隔板的单箱多室波形钢腹板箱梁荷载横向分布系数，在L/2偏载工况下，边梁的计算结果与试验结果误差为6.91%，与有限元计算结果误差为5.91%，与跨中有横隔板的有限元计算结果误差为13.20%;在L/2中心加载工况下，中梁的计算结果与试验及有限元计算误差均为4.79%，与跨中有横隔板的有限元计算结果误差为0.59%.2种工况下，刚接梁法计算结果与试验及有限元误差均小于7%，与有中横隔板的有限元结果相比，偏于安全.该方法适用于有、无中横隔板的单箱多室波形钢腹板箱梁的荷载横向分布系数计算.

3 荷载横向分布沿桥跨的变化

3.1 弯矩分布

试验梁底板弯矩的横向分布曲线如图8(a)所示，荷载作用的横向位置对单箱双室波形钢腹板箱梁弯矩的横向分布影响很大，纵向位置影响不大.故无中横隔板的单箱双室波形钢腹板箱梁，弯矩横向分布系数沿桥跨可统一采用由刚接梁法计算的L/2处的横向分布系数mc.

3.2 支反力分布

试验梁梁端支反力的横向分布曲线如图8(b)、(c)所示.随着荷载从L/2向梁端移动，支反力的分布越来越不均匀.梁端、L/8中心加载时，荷载作用处主梁承担大部分荷载;L/4，3L/8，L/2截面中心加载时，支反力横向分布与L/2，L/4的弯矩横向分布相似.桥跨内各截面作用偏载时，梁端支反力横向分布均表现为荷载作用处主梁承担大部分荷载，离荷载较远处主梁基本不承担荷载.

设梁端处采用杠杆原理法计算的荷载横向分布系数为m0，L/2截面处采用刚接梁法计算的荷载横向分布系数为mc.由图8(b)、(c)可见，中梁支反力横向分布系数在梁端采用过于保守，建议采用0.6m0，L/4～L区段内可采用mc，梁端至L/4区段，呈直线形过渡;边梁支反力横向分布系数沿桥跨可采用 0.9m0.

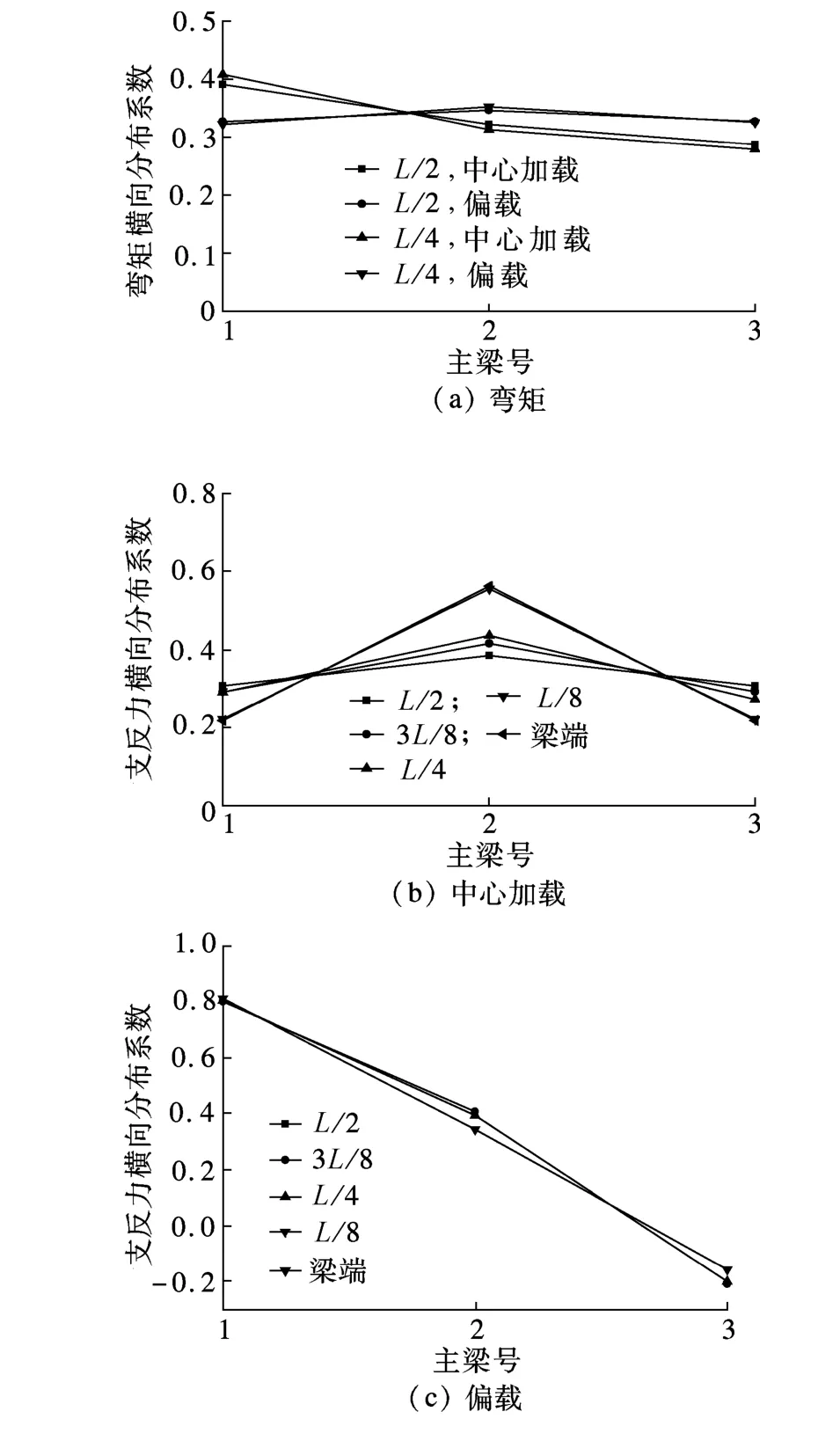
图8 弯矩及支反力横向分布

4 结论

1)本文基于无中横隔板的情况，推导出单箱多室波形钢腹板箱梁荷载横向分布系数的计算公式，考虑了各主梁的抗弯、抗扭刚度及各主梁间距的差别，其力学概念清晰，应用范围广泛.

2)刚接梁法计算结果与试验及有限元计算结果的误差均小于7%，与考虑中横隔板的有限元计算结果相比，偏于安全.该方法适用于有、无中横隔板的单箱多室波形钢腹板箱梁的荷载横向分布系数计算.

3)单箱双室波形钢腹板箱梁的横向分布系数沿桥跨分布规律为:弯矩可统一采用mc;中梁支反力在梁端采用0.6m0，L/4～L区段内采用mc，梁端至L/4区段，呈直线形过渡;边梁支反力可统一采用 0.9m0.

［1］李淑琴，陈建兵，万水，等.我国几座波形钢腹板PC组合箱梁桥的设计与建造 ［J］.工程力学，2009，26(S1):115-118.

Li Shuqin，Chen Jianbing，Wan Shui，et al.Application of the prestressed concrete box girder with corrugated steel webs in bridge engineering in China［J］.Engineering Mechanics，2009，26(S1):115-118.(in Chinese)

［2］孙广华.公路曲线梁桥内力横向分配计算［J］.南京工学院学报，1988，18(1):94-104.

Sun Guanghua.Calculation of transverse distribution of internal forces in highway curved girder bridges［J］.Journal of Nanjing Institute of Technology，1988，18(1):94-104.(in Chinese)

［3］孙广华.箱形梁桥内力横向分配计算方法［J］.南京工学院学报，1986，16(3):110-120.

Sun Guanghua.Method for determination of the lateral distribution of internal forces in box-girder bridges［J］.Journal of Nanjing Institute of Technology，1986，16(3):110-120.(in Chinese)

［4］Tarhini K M，Frederick G R.Lateral load distribution in I-girder bridges［J］.Computers and Structures，1995，54(2):351-354.

［5］Tarhini K M，Frederick G R.Wheel load distribution in I-girder highway bridges［J］.Journal of Structural Engineering，ASCE，1992，118(5):1285-1294.

［6］聂鑫，樊健生，付裕.箱形截面连续组合梁桥的荷载横向分布 ［J］.清华大学学报:自然科学版，2010，49(12):1930-1933.

Nie Xin，Fan Jiansheng，Fu Yu.Transverse load distribution on box section continuous composite steel-concrete bridges［J］.J Tsinghua Univ:Sci＆Tech，2010，49(12):1930-1933.(in Chinese)

［7］聂建国，张晓光，樊健生，等.钢-混凝土组合梁加宽混凝土梁桥的横向分布系数［J］.清华大学学报:自然科学版，2010，50(6):805-809.

Nie Jianguo，Zhang Xiaoguang，Fan Jiansheng，et al.Transverse distribution coefficient of concrete bridges widened with steel concrete composite beams［J］.J Tsinghua Univ:Sci＆Tech，2010，50(6):805-809.(in Chinese)

［8］Abbas H H，Sause R，Driver R G.Behavior of corrugated web I-girders under in-plane loads［J］.Journal of Engineering Mechanics，ASCE，2006，132(8):806-814.

［9］Kövesdi B，Jáger B，Dunai L.Stress distribution in the flanges of girders with corrugated webs［J］.Journal of Constructional Steel Research，2012，79:204-215.

［10］Nguyen N D，Han S-R，Kim J-H，et al.Moment modification factors of I-girder with trapezoidal web corrugations under moment gradient［J］.Thin-Walled Structures，2012，57:1-12.

［11］Mo Y L，Fan Y.Torsional design of hybrid concrete box girders［J］.Journal of Bridge Engineering，ASCE，2006，11(3):329-339.

［12］Elgaaly M，Seshadri A，Hamilton R.W.Bending strength of steel beams with corrugated webs［J］.Journal of Structural Engineering，ASCE，1997，123(6):772-782.

Load transverse distribution of single box multi-cell girder with corrugated steel webs

Ma Lei Wan Shui Jiang Zhengwen Li Minghong
(School of Transportation，Southeast University，Nanjing 210096，China)

Abstract:A formula for calculating the load transverse distribution coefficient of single box multicell girder with corrugated steel webs was deduced by the rigid connected beam method on the basis of the equivalent plane plate-girder model.Then，a test on a single box double-cell girder with corrugated steel webs was carried out to research its load transverse distribution.The research results show that the error between the load transverse distribution coefficient calculating with rigid connected beam method and that obtained from test and finite element analysis is less than 7%.Compared with the finite element analysis result of the girder with midspan diaphragm，the load transverse distribution coefficient calculated by the rigid connected beam method is relatively safe.Thus the rigid connected beam method can be used to calculate the load transverse distribution coefficient of the single box double-cell girder with corrugated steel webs where or not there is a diaphragm in the midspan of the girder.The distribution law of the load transverse distribution coefficient along the longitudinal of single box multi-cell girder with corrugated steel webs was suggested according to the experimental results.The moment transverse distribution coefficients aremc，wheremcis the load transverse distribution coefficient at the middle span calculated by the rigid beam method.For the support reaction transverse distribution coefficients of the middle girder，0.6m0is used at the end，wherem0is the load transverse distribution coefficient at the end calculated by the level principle method;mcis applicable fromL/4 toL;and the transition from the end toL/4 is linear.The support reaction transverse distribution coefficients of the side girder are 0.9m0.

Key words:bridge engineering;single box multi-cell;corrugated steel webs;rigid connected beam method;load transverse distribution

中图分类号:TU375

A

1001－0505(2014)01-0145-05

doi:10.3969/j.issn.1001 －0505.2014.01.026

收稿日期:2013-07-27.

马磊(1982—)，女，博士生;万水(联系人)，男，博士，教授，博士生导师，lanyu421@163.com.

基金项目:国家自然科学基金资助项目(50078014)、河南省交通运输厅科技资助项目(2010P247).

马磊，万水，蒋正文，等.单箱多室波形钢腹板箱梁荷载横向分布［J］.东南大学学报:自然科学版，2014，44(1):145-149.［doi:10.3969/j.issn.1001 －0505.2014.01.026］