中空环形行波超声波电机有限元接触模型

蒋春容 胡敏强 金 龙 徐志科

(1东南大学电气工程学院，南京 210096)(2南京工程学院电力工程学院，南京 211167)

中空环形行波超声波电机有限元接触模型

蒋春容1，2胡敏强1金 龙1徐志科1

(1东南大学电气工程学院，南京 210096)
(2南京工程学院电力工程学院，南京 211167)

摘 要:采用有限元法建立了佳能镜头上使用的中空环形行波超声波电机定转子接触模型.通过建立定转子有限元接触模型并在定子中性面上施加行波运动，得到定子齿表面质点的斜椭圆运动及其与转子的接触状态，比较了空载和堵转情况下定转子接触表面质点的法向和切向运动及定转子接触压力分布.空载和堵转时接触压力分布有明显不同，表明负载转矩对接触压力分布有影响.用实验数据对提出的理论模型进行了验证，理论分析结果与实验数据基本吻合.最后，对电机转子结构提出了改进方法，理论分析表明，采用改进后的转子，电机的转矩-转速特性有了明显改善.

关键词:超声波电机;中空环形;接触模型;有限元法

超声波电机利用压电陶瓷的逆压电效应，通过摩擦直接驱动转子或滑块.环形行波超声波电机是应用最多的一种超声波电机，其优点表现为低速大转矩、动态响应快、断电自锁等，在光学系统、医疗器材、航空航天等领域有广阔的应用前景［1-2］.

超声波电机所有的输出能量均要通过定转子间的摩擦耦合来传递.对超声波电机接触摩擦模型的研究，主要集中在摩擦材料粘接在转子［3-9］或定子［10-12］表面的超声波电机上.目前照相机镜头采用的中空超声波电机均为无摩擦材料的超声波电机.采用无摩擦材料的超声波电机，即定转子经过金属表面处理后直接接触，减少了电机装配时摩擦材料的粘接过程，可从结构上改进超声波电机控制的精度和特性.关于无摩擦材料的定转子接触摩擦模型，Maeno等［13-14］在20年前用有限元法对佳能镜头上采用的中空超声波电机进行研究，在对定子进行模态分析后，指出由于定子齿的存在，定子表面质点的椭圆运动轨迹为斜椭圆，但在定转子接触模型中，没有考虑到定子齿质点的斜椭圆运动，直接给定子齿质点施加长轴与短轴均与坐标轴平行的正椭圆运动，因此模型有待进一步改进.

本文在Maeno等研究的基础上，以佳能镜头上的超声波电机为研究对象，进一步研究定转子有限元接触模型，通过在定子中性面施加行波运动的方式，得到定子齿质点的斜椭圆运动及其与转子的接触状态，计算电机输出性能，提出了转子的改进方法，并用Maeno等的实验数据验证了理论模型.

1 定子运动方程

佳能相机镜头用的中空电机结构如图1所示，电机的定子由金属弹性体和经过极化处理的压电陶瓷组成，转子通过预压力压在定子上表面.

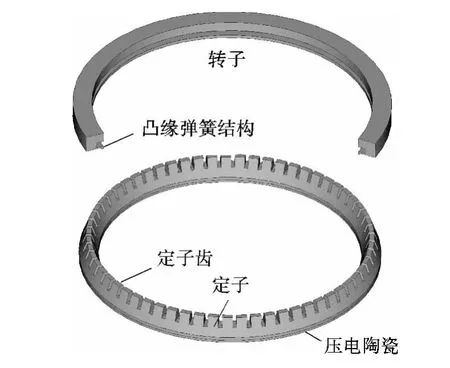
图1 中空环形行波超声波电机

由于电机工作时转子上施加的法向预压力很小，仅为15 N［13］，因此忽略预压力对定子振动的影响，认为定子振动的振幅为固定值.根据克希霍夫薄板理论，采用静止柱坐标系(r，θ，z)，定子中性面弯曲行波可表示为

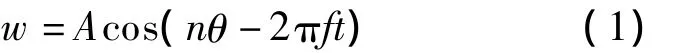
式中，w表示定子中性层某质点的法向位移;A为超声振动的振幅;n为定子圆周上的波数;f为外加激振电压的频率.定子表面质点的法向位移wn与中性层质点的法向位移w相同.由中性层弯曲行波诱发的定子表面质点的切向位移wt为

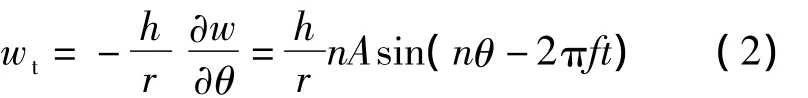
式中，h为定子上表面到中性层的距离;r为定转子有效接触半径.定子表面质点的运动轨迹为

式(3)表明，定子表面质点运动轨迹为椭圆.

2 定转子有限元接触模型

在建立定转子有限元接触模型时，由于中性面的运动已知，因此将定子中性面以下的部分略去而只考虑中性面及其以上的部分.定子复合梁中性面的位置可根据材料力学的方法来确定［15］.

本文采用有限元计算软件ANSYS建立定转子的有限元接触模型(见图2).选择八节点六面体单元SOLID185对定转子划分网格，考虑到定转子的结构特殊性，采用扫略网格划分方法.定转子接触问题属于面-面接触，目标面和接触面都是柔性的，在建立定转子接触对时，由于定子比转子有更大的弹性模量，因此，将定子上表面定义为目标面，把与定子接触的转子下表面定义为接触面，使用三维目标单元TARGE170与三维接触单元CONTA173定义面-面接触对.目标单元和接触单元覆盖在分析模型接触面之上，并给接触对分配实常数号，构成接触对的目标单元和接触单元通过共享的实常数号联系起来.指定定转子间的动摩擦系数μd和静摩擦系数μst.为使模型更符合电机实际运行时的状态，给模型施加如下的边界条件和载荷:①在定子中性面节点上施加位移载荷，使中性面作如式(1)所示的行波运动;②给定子中性面的内侧节点施加径向和周向的位移约束，以阻止定子的平面平移运动和周向旋转运动;③ 转子上表面的节点耦合轴向自由度，即转子上表面节点轴向位移一致;④在转子的上表面施加轴向预压力F;⑤给转子上表面节点施加径向位移约束，使转子只做周向旋转运动而不做平面平移运动;⑥ 负载转矩以等效切向力的方式施加在转子上表面内侧节点上.

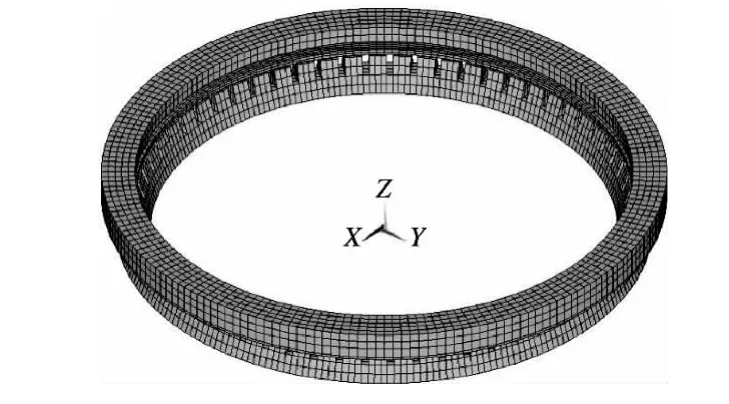
图2 有限元接触模型

考虑到接触问题的高度非线性，模型中忽略了转子的惯性，对定转子稳态接触情况进行求解.分析求解时设定结束时间为定子振动的一个周期，即定子行波行进一个波长所需的时间，并使每一子步时间步长Δt不超过0.5 μs，以使每一子步定子的变形变化量足够小.

3 仿真结果与分析

接触模型的参数如表1所示，其中，Es和Er分别为定子和转子的弹性模量，υs和υr分别为定子和转子的泊松比.

表1 接触模型参数

在转子表面施加预压力，初始时刻定转子的变形如图3所示，转子在预压力作用下发生了变形，定转子在靠近波峰处相接触.

图4 定子表面质点的运动轨迹

定子齿质点的运动轨迹如图4所示，其中图4(b)中的编号对应于图4(a)中的各质点编号.由于定子齿的存在，定子齿表面质点椭圆运动轨迹的轴与坐标轴并不平行.这一结果与Maeno等通过对定子进行模态分析得到的结果［13］一致.定子齿的存在放大了定子质点的切向运动，越靠近齿顶端，放大作用越明显.

为便于比较，给转子接触面上的质点编号，如图5(a)所示，其中a点和b点分别为转子与定子接触面上内径处和外径处的质点.转子空载时，在一个振动周期内，定转子接触表面质点的法向位移wnc如图5(b)所示.由图可知，由于转子柔性变形，转子质点b与定子齿面接触，而转子质点a并不与定子齿面接触，定转子接触区径向接触宽度仅为转子下表面实际径向宽度的10%左右.一个周期内，b点与定子齿接触的时间占周期的40%，也可等效地认为:在一个波长内，定转子最大切向接触长度占波长的40%.将位移对时间求导数即可得到定转子接触区质点的法向速度.转子堵转时，定转子接触表面质点的法向位移和速度与空载时并无太大区别，这表明负载转矩对定转子接触表面质点的法向运动没有影响.

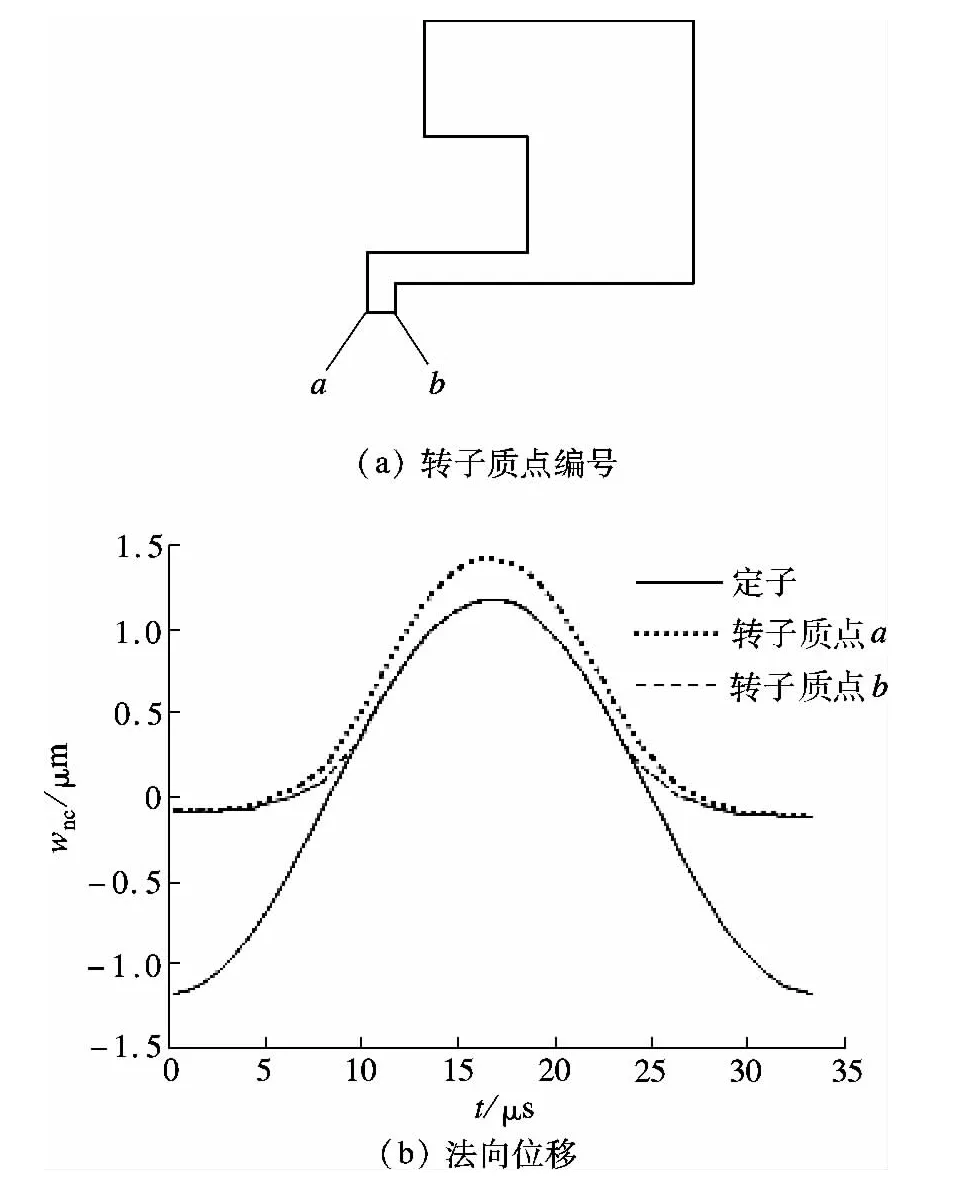
图5 空载时定转子接触点的法向位移

图6为15 N的预压力作用下，转子空载和堵转时，定转子接触表面质点的切向速度vtc分布.空载和堵转时定子表面质点的切向速度没有明显区别，所不同的是转子质点的切向速度.空载时，转子质点a和b的速度在一定范围内波动，在一个周期内的平均值约为0.15 m/s，堵转时，转子接触区质点的切向速度除了在个别时刻为零，其余时刻并不为零，但在一个周期内的平均值为零.

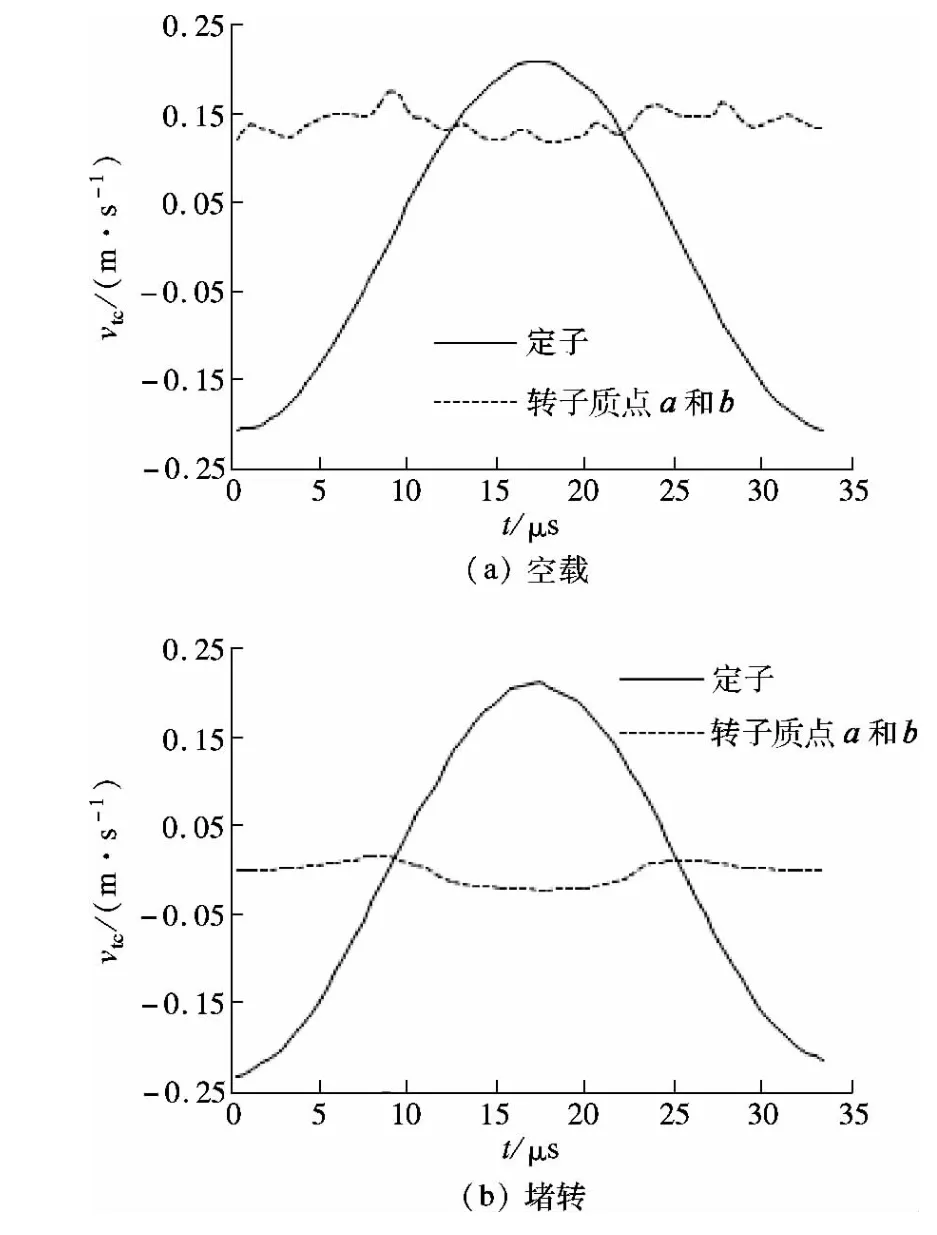
图6 定转子接触表面质点的切向速度

图7 定转子接触压力分布

图7为空载和堵转时转子质点b点的接触压力P的分布.由于转子质点a不与定子接触，故压力为零.空载和堵转情况下，定转子切向接触长度相同，但接触压力分布有较大区别，空载时转子质点b的接触压力近似关于定子行波波峰对称，堵转时接触压力不再是对称分布，说明负载对接触压力的分布有显著影响.

4 实验验证

为了验证有限元接触模型，将仿真分析得到的电机转矩-转速(T-n)曲线与实测数据进行比较，如图8所示.实线为有限元模型仿真结果，其中转速为一个振动周期内的平均值.实验数据来自于文献［14］.由图可知，仿真结果与实验结果基本吻合，验证了有限元接触模型的有效性.

图8 仿真结果与实验结果比较

5 转子结构的改进

由以上分析可知，由于转子柔性变形，定转子实际的径向接触宽度很有限，因此提出了如图9所示的转子结构，将原来转子结构称为L型转子，新的转子结构称为U型转子，2种结构的转子与原有定子接触时具有相同的接触半径，且2种转子的总高度相同.同样按照前述方法建立U型转子的定转子接触模型，采用相同的定子，比较采用L型转子与采用U型转子时电机的性能差异.15 N预压力下电机的转矩-转速曲线如图10所示，由图可知，采用L型转子时，堵转力矩和空载转速分别为0.15 N·m和46 r/min，采用U型转子时，堵转力矩和空载转速分别达到0.17 N·m和50 r/min，因此，采用U型转子，电机性能得到了改善.究其原因，是由于2种结构的转子与定子接触时，接触面积不同，当施加相同的预压力时，采用U型转子结构时接触面积更大，而采用L型转子，仅在转子外侧边缘小部分区域接触，接触压力高度集中，并且U型转子切向接触长度小于L型转子，这就意味着减小了定子切向速度较低的表面质点与转子的接触，使定转子接触区内阻碍转子运动的区域减小，从而提高了转矩和转速.

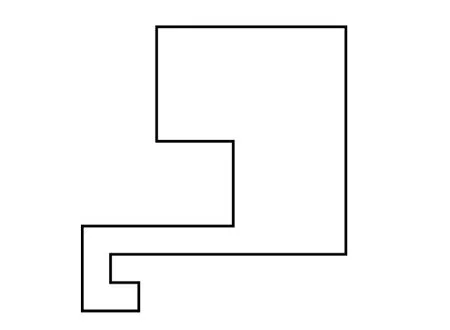
图9 U型转子结构

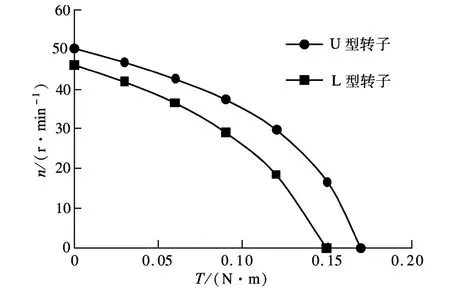
图10 U型转子和L型转子电机的转矩转速曲线比较

6 结论

1)定子齿的存在放大了定子质点的切向运动，但定子齿表面质点椭圆运动轨迹的轴与坐标轴并不平行，即定子表面质点作斜椭圆运动.

2)负载转矩对定转子接触表面质点的法向运动没有明显影响，对定子表面质点的切向运动也没有明显影响，但对定转子接触压力分布有显著影响.

3)将理论分析结果与实验数据相比较，二者基本吻合，验证了所提出的理论模型.

4)对转子结构进行了改进，提出了U型转子结构，并比较了U型转子和L型转子电机的转矩-转速曲线，表明U型转子电机的转矩-转速曲线优于L型转子电机.

［1］Bekiroglu E.Ultrasonic motors:their models，drives，controls and applications［J］.Journal of Electroceramics，2008，20(3/4):277-286.

［2］胡敏强，金龙，顾菊平.超声波电机原理与设计［M］.北京:科学出版社，2005:17-20.

［3］徐志科，胡敏强，金龙.行波超声波电机的动力学模型仿真［J］.东南大学学报:自然科学版，2008，38(6):1072-1076.

Xu Zhike，Hu Minqiang，Jin Long.Research on dynamic model of traveling wave type ultrasonic motor［J］.Journal of Southeast University:Natural Science Edition，2008，38(6):1072-1076.(in Chinese)

［4］Wallaschek J.Contact mechanics of piezoelectric ultrasonic motors［J］.Smart Material and Structure，1998，7(3):369-381.

［5］刘锦波，陈永校.超声波电机定转子接触的摩擦传动模型及其实验研究［J］.中国电机工程学报，2000，20(4):59-63.

Liu Jinbo，Chen Yongxiao.Investigation on contact model of ultrasonic motor and its experiments［J］.Proceedings of the CSEE，2000，20(4):59-63.(in Chinese)

［6］Storck H，Wallaschek J.The effect of tangential elasticity of the contact layer between stator and rotor in travelling wave ultrasonic motors［J］.International Journal of Non-Linear Mechanics，2003，38(2):143-159.

［7］Radi B，Hami A E.The study of the dynamic contact in ultrasonic motor［J］.Applied Mathematical Modelling，2010，34(12):3767-3777.

［8］周盛强，赵淳生，黄卫清.旋转型行波超声电机接触界面的空间域分析［J］.中国电机工程学报，2010，30(12):63-68.

Zhou Shengqiang，Zhao Chunsheng，Huang Weiqing.Contact analysis of traveling wave type rotary ultrasonic motor in space domain［J］.Proceedings of the CSEE，2010，30(12):63-68.(in Chinese)

［9］Sattel T，Hagedorn P，Schmidt J.The contact problem in ultrasonic traveling-wave motors［J］.Journal of Applied Mechanics，Transactions ASME，2010，77(3):1-11.

［10］曲建俊，孙凤艳，田秀.粘弹性接触层在定子表面的行波超声电动机接触模型［J］.机械工程学报，2006，42(12):175-179.

Qu Jianjun，Sun Fengyan，Tian Xiu.Contact model of traveling wave ultrasonic motor with visco-elastic contact layer on stator surface［J］.Chinese Journal of Mechanical Engineering，2006，42(12):175-179.(in Chinese)

［11］Qu Jianjun，Sun Fengyan，Zhao Chunsheng.Performance evaluation of traveling wave ultrasonic motor based on a model with visco-elastic friction layer on stator［J］.Ultrasonics，2006，45(1/2/3/4):22-31.

［12］王彦利，曲建俊，田秀.摩擦材料应用方式对超声波电机驱动特性的影响［J］.摩擦学学报，2010，30(4):321-327.

Wang Yanli，Qu Jianjun，Tian Xiu.Effect of application mode of friction material on driving characteristics of ultrasonic motor［J］.Tribology，2010，30(4):321-327.(in Chinese)

［13］Maeno T，Tsukimoto T，Miyake A.Finite-element analysis of the rotor/stator contact in a ring-type ultrasonic motor［J］.IEEE Transactions on Ultrasonics，Ferroelectrics，and Frequency Control，1992， 39(6):668-674.

［14］Maeno T，Bogy D B.FE analysis and LDA measurement of the dynamic rotor/stator contact in a ring-type ultrasonic motor［J］.Journal of Tribology，1993，115(4):625-631.

［15］刘鸿文.材料力学Ⅰ［M］.4版.北京:高等教育出版社，2004:138-140.

Finite element contact model of a hollow ring type traveling wave ultrasonic motor

Jiang Chunrong1，2Hu Minqiang1Jin Long1Xu Zhike1

(1School of Electrical Engineering，Southeast University，Nanjing 210096，China)
(2School of Electric Power Engineering，Nanjing Institute of Technology，Nanjing 211167，China)

Abstract:The focus of this paper is to study the contact model of a hollow ring type traveling wave ultrasonic motor used in the Canon auto-focus lens with the finite element method.First，the finite element contact model is built and the traveling wave motion is applied to the neutral plane of the stator.The sloping elliptical motion of the stator surface and the contact status of the stator and the rotor are obtained.The motion of the stator and the rotor as well as the contact pressure in the contact surface are compared when the rotor is applied with no load torque and stalled.The contact pressure when the rotor is applied with no load is significantly different from the contact pressure when the rotor is stalled，which indicates that the load torque has an effect on the distribution of contact pressure.Then the proposed model is verified by experimental data.The analytical results are in good agreement with the experimental results.Finally，a new rotor is proposed and it is indicated that the torque-speed performance of the motor is optimized by adopting the new rotor.

Key words:ultrasonic motor;hollow ring type;contact model;finite element method

中图分类号:TM356

A

1001－0505(2014)01-0099-05

doi:10.3969/j.issn.1001 －0505.2014.01.018

收稿日期:2013-05-26.

蒋春容(1983—)，女，博士，讲师;胡敏强(联系人)，男，博士，教授，博士生导师，mqhu@seu.edu.cn.

基金项目:国家自然科学基金资助项目(51177014，51077011)、南京工程学院校级科研基金资助项目(YKJ201317).

蒋春容，胡敏强，金龙，等.中空环形行波超声波电机有限元接触模型［J］.东南大学学报:自然科学版，2014，44(1):99-103.［doi:10.3969/j.issn.1001 －0505.2014.01.018］