基于ARIMA模型的产业集群稳定性研究
2014-09-14吴绍玉WUShaoyu张劲松ZHANGJinsong
吴绍玉 WU Shao-yu;张劲松 ZHANG Jin-song
(天津市地下铁道运营有限公司,天津300222)
0 引言
影响产业集群稳定性的因素一般包括集群外部因素和集群内部因素。集群外部因素对产业集群稳定性的影响可以称为“外来扰动”。随着技术发展过程中,“外来扰动”因素的改变,总会引起相关市场的激烈反应以及相关政策和方针的制定。这种影响也会直接作用于相关产业链,进而影响以此产业链相关联的产业集群发展的稳定性。例如卡伦堡工业园区中,石膏生产技术的改变,导致产业链断裂,产业集群失衡。日本“3.11”地震,引起天津一汽汽车生产工艺减缓和停滞。由此可见,科学的预测“外来扰动”因素对产业集群稳定性的影响,并据此对产业集群的相关产业链进行技术调整,有助于提高产业集群的稳定性和生态园发展的持续性。
1 文献综述
近几年,学者们对于产业集群稳定性的研究多采用Logistic模型分析的方法,由不同的角度:协同影响因素[1]、企业自组织[2]、产业集群演化[3]、集群结构[4]、产业集群的互存互利[5]等角度进行了研究,上述文献都提出在Logistic模型中假设企业的产出量是一个与时间相关的函数。集群的产出量与所消耗的区域资源量成线性关系,并且假设产业集群内经济不受其他区域以外的因素影响[5]。
但并没有指出的是:
①集群产出量函数并不是完全依赖于时间的函数,它与时间有一定的统计关系,但并非完全依赖于时间。集群产出量和区域资源量也并不总是成线性关系,但集群发展到一定程度,技术、政策和地域等因素同样也会成为制约集群产出量和稳定性的决定性因素。
②Logistic模型是建立在假设没有任何“外来扰动”,既不受集群区域以外因素影响的条件下,副产品交换量或市场容纳量受技术、资本、市场规模等既定条件约束[6]。但是技术创新和制度创新,以及自然和社会环境的突发变化,时有发生,在这些“外来扰动”的影响下,Logistic模型的理论基础受到了猛烈的冲击。这就急需使用新的方法,在考虑“外来扰动”的情况下,对产业集群的稳定性加以讨论。
当然,国内其他学者也采用定性的方法分析产业集群的稳定性,如蒋云霞和肖华茂两位学者由博弈视角指出了产业集群中企业合作博弈的得益矩阵,提出集群生态网络中企业之间的生态合作是各个网络节点上的企业与其相关企业之间利益博弈均衡所形成的结果[7]。
可见国内并未有囊括“外来扰动”因素对于产业集群稳定性影响的分析,而本文是综合考虑产业集群“外部扰动”、内部因素和时间因素对企业产出量的影响,运用时间序列分析的方法,建立ARIMA模型,讨论产业集群的稳定性。
2 ARIMA模型
2.1 ARIMA模型 ARIMA模型,全称为自回归移动平均模型(Autoregressive Integrated Moving Average Model,ARIMA)。该模型最早由是由博克思(Box)和詹金斯(Jenkins)于70年代初提出的著名时间序列预测方法,所以又称为Box-jenkins模型、博克思-詹金斯法。ARIMA模型也写作为ARIMA(p,d,q),其中AR表示是自回归,p为自回归项;MA表示移动平均,q为移动平均项数,d为所选择数据转化为平稳时间序列时所做的差分次数。ARIMA模型建模过程主要分为三个基本步骤。首先是模型的识别(identification),确定模型中p、d、q的值。然后是模型的参数估计(estimation),由历史数据确定模型中各参数。最后是模型的诊断与预测(prediction),检验模型误差以及运用既得模型进行数据预测[8]。ARIMA模型可能会比一般的预测技术要更加复杂,但是如果运用得当,它会十分的灵活有力[9]。
2.2 模型与数据的选择 在统计学的观点中,所谓时间序列就是指将某个指标的一组在时间上连续的数据,按时间顺序排为一列所形成的序列。这一组数据具有随机性,彼此之间存在着统计学上的依赖性。
ARIMA模型时间序列模型的一种,因此这一模型的使用前提首先是要求数据的随机性和统计依赖性。然后根据收集到的数据,通过绘制散点图、自相关函数和偏自相关函数图,并利用ADF单位根检验其方差、趋势及其季节性变化规律,以对序列的平稳性进行识别,转化为时间序列模型的一般形式ARMA模型,进行求解。值得指出的是一般来讲,经济运行的时间序列都不是平稳序列。这也正是本文采用ARIMA模型的原因。
3 ARIMA模型建立
“外来扰动”和内部因素对产业集群影响集中表现在于产业集群的产出量上,而时间序列序列模型是建立在平稳时间序列基础上的。但现实中的数据很多并非完全严格上的平稳,因此首先对所选数据进行差分,经过有限次的差分处理,将数据转化为平稳序列。
本文采用2010年1月-2011年2月,我国某汽车产业集群汽车产出量数据进行模拟建模。所用数据均来自中国统计局网站,并将数据整理如表1所示。

表1 某汽车产业集群汽车产出量
3.1 模型的识别 首先将此时间序列命名为Xt,利用EViews 6.0软件做出其时间序列图,如图1,但仅通过图像无法准确得知Xt是否为平稳时间序列,因此需要对Xt的平稳性进行检验,本文采用假设检验的原理,即
设 原假设为:Xt是非平稳时间序列;
被择假设为:Xt是非平稳时间序列。
同时做出Xt的ADF单位根检验结果如图2所示。
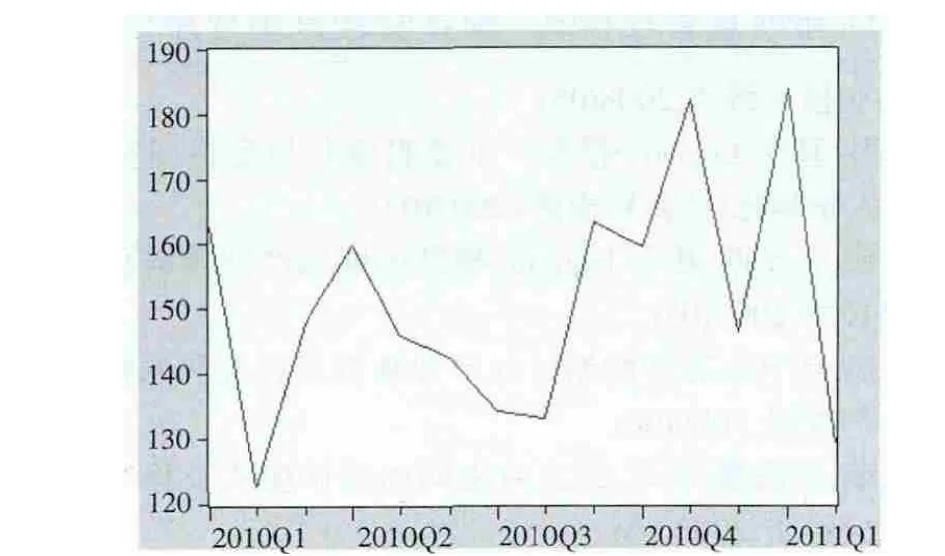
图1 Xt的时间序列图
由图2可见Xt的Prob=0.0142很小,在10%的显著性水平下,Prob<0.1,拒绝原假设。即,Xt是平稳时间序列,序列对象不存在单位根。因而Xt是0阶单整,记为I(1),ARIMA(p,d,q)模型中的 d=0。
随后,需要确定 ARIMA(p,d,q)中 p 和 q 的取值,由图3中Xt的相关序列图可以看出,Xt的自相关系数(Autocorrelation,AC)3阶后显著趋于0,偏自相关系数(Partial Correlation,PAC)2阶后显著趋于0,则可以判定ARIMA 模型的 p=3,q=2。

图2 Xt的ADF单位根检验
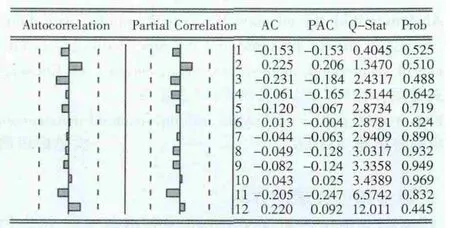
图3 Xt的相关序列图
3.2 模型的参数估计 确定ARIMA模型之后,需要对ARIMA模型参数进行估计,在EViews的帮助下,参数的估计变得简单,但在模型参数估计之后仍需对ARIMA模型进行校正和修改。Xt的最终ARIMA模型参数如图4所示,为 ARIMA(0,0,2)模型。


图4 Xt的ARIMA模参数
3.3 模型的诊断 为了确定该模型是否可以用于预测,需更进一步对其进行白噪声检验,通过检验后的模型才可用于预测。用EVeiws做出其对应的残差序列的自相关函数和偏自相关函数如图5所示(取滞后系数为12)。

图5 Xt残差残差序列的自相关函数和偏自相关函数
由图5可知残差对应的自相关系数与偏自相关系数的Prob值均大于显著性水平5%,且在置信区间内,可以认为该残差为白噪声过程。又该样本量为14,所以最大滞后期为n≈4=,在图5中对应的检验数为3.9020,在95%的显著性检验水平下,相应χ2的分布的α检验数为(4)=9.4877。由于 3.9020<(4)=9.4877,所以模型检验通过。即该产业集群产出量可用式(1)表示。
3.4 模型的运用 在得出产业集群的ARIMA模型之后,可以依据这一模型对该产业集群的稳定性进行预测与研究。如上文所示的ARIMA模型:Xt为理论当月产出量计算值,实际当月产出量Q可根据情况若在一定范围(Xt±φ)内,则当前集群较为稳定。
4 结论与启示
通过时间序列模型的建模可以看出,该模型在分析产业集群稳定性时,并没有排除“外来扰动”因素对于产业集群的影响,它所使用的数据产业集群产出量,是受到集群内外部因素共同作用的结果,具有一定的普适性。且在专业工具的使用下,易得出确切的数据和理论模型。
[1]于树江,李双燕.基于协同影响因素的产业集群共生稳定性分析[J].商业时代,2010(05).
[2]李南,李忠华.河北省临港产业集群的稳定性与动态演化研究[J].工业技术经济,2008(05).
[3]程胜.基于Logistic模型产业集群演化稳定性研究[J].西北农林科技大学学报(社会科学版),2007(03).
[4]张会,张光明.基于Logistic模型的船舶产业集群稳定性分析[J].造船技术,2007(05).
[5]卢杰.基于生态学的制造业产业集群共存互利的稳定性模型[J].统计与决策,2009(08).
[6]张萌,姜振寰,胡军.工业共生网络运作模式及稳定性分析[J].中国工业经济,2008(06).
[7]蒋云霞,肖华茂.基于博弈视角的产业集群生态网络稳定性分析[J].科技管理研究,2010(01).
[8]Matteo.M.Pelagatti.Modeling and Simulation in Science,Engineering and Technology,Neural Networks and Sea Time Series,2006:111-131.
[9]J.M.Hsiao,C.J.The International Journal of Advanced Manufacturing Technology,2005,27(5-6):604-609.
