外侧膝状体细胞对边缘的响应模型

任 远

(上海电机学院 电子信息学院， 上海 200240)

外侧膝状体细胞对边缘的响应模型

任 远

(上海电机学院 电子信息学院， 上海 200240)

边缘检测是机器视觉系统与生物视觉系统处理视觉信息的基础阶段。为初级视觉通路中的外侧膝状体(LGN)细胞建立一个模型，描述其对边缘的响应，为构建基于神经机制的图像处理方法提供特征表征。根据神经节细胞感受野的生理特性，用经典的高斯差模型描述LGN细胞对刺激的响应，通过合理地简化得到相对简单的响应函数。通过简单数学分析，能够得到函数的几点数学性质，且这些性质都与神经元的生理特性相符。进一步简化刺激的对比度，得到归一化的响应函数。数值实验发现，函数的响应曲线和神经科学研究得到的生理曲线具有相似性，说明该数学模型的合理性。

外侧膝状体； 边缘； 感受野； 响应曲线； 高斯差

无论是生物视觉系统还是机器视觉系统，边缘检测都是视觉信息处理的一个基础环节和首要步骤。在初级视觉通路中，视网膜是一个感光组织，位于眼球壁的内侧。它接收眼睛传来的光信号，将光信号转换成电信号并进行初步处理。神经节细胞的轴突形成视神经纤维，将处理后的信号传递到外侧膝状体(Lateral Geniculate Nucleus, LGN)。LGN处于初级视觉通路的中间环节，它综合来自视神经的信息(颜色、双眼视差和频率等)。一般认为，LGN中继细胞最主要的功能是将视网膜编码的信息几乎不加修改地复制到皮层中。神经节细胞与LGN细胞为后续皮层处理提供了基础数据，复杂的视觉任务，如识别面部、物体及手写体等都依赖于这些数据，因而许多研究都集中在模拟这两种细胞的信息处理机制上。为了给LGN细胞构建一个数学模型，本文不区分LGN细胞和神经节细胞在生理上各方面的差异，而认为两者在功能上是相等的。

每个视觉神经元只对视网膜特定区域内的视觉刺激产生直接反应，这个区域称为该视觉细胞的感受野。感受野是神经科学研究的核心概念之一。文献[5-6]中在Kuffler提出的同心圆结构感受野的基础上，采用高斯差(Difference of Gaussians, DOG)模型来描述神经节细胞的感受野。DOG模型将光刺激产生的神经元信号分为中心和周边两种成分，这两种成分的差即为神经元对刺激的实际反应。中心区和周边区在空间上呈同心圆结构，两者相互重叠，周边区更大。中心区和周边区的响应机制均可以采用高斯函数拟合。这两个高斯函数的差值把神经节细胞的感受野敏感性分布描述成一个墨西哥草帽形结构: 中心区高斯函数的敏感度较高；周边区高斯函数的符号与中心区相反，敏感度下降较平缓。利用感受野的概念，神经科学家对神经节细胞的性质进行了深入研究。许多学者研究了神经节细胞的对比度敏感性(Contrastsensitivity)[8-9]。对于神经节细胞对对比边缘的响应性质这一问题，文献[10]中研究了神经节细胞对在其感受野内移动的边缘的响应，并利用一个DOG的变形给出了解释。文献[11]中用一个复杂的非线性模型拟合了这条曲线。文献[12]中研究了具有变化模糊度的对比边缘如何影响神经节细胞的响应。文献[13]中总结了现有模型在解释神经节细胞如何集成空间信号方面的成功和不足之处。本文尝试利用已有的DOG模型，定量描述了LGN细胞对一种在自然场景和数字图像中都普遍存在的刺激即边缘响应，为构建基于更高层神经元处理视觉信息的数字图像处理方法提供对边缘的基础表征。

1 基于对比刺激的DOG模型

本文考虑LGN对两种不同强度刺激构成的边缘的响应问题。如图1所示，一个神经元的感受野被一个对比刺激所覆盖，其中，c1和c2分别为两种不同的刺激强度，w为较强刺激覆盖感受野的宽度。设感受野的中心区和周边区的半径分别为rc和rs，并将这两个区域分别记为Rc和Rs。

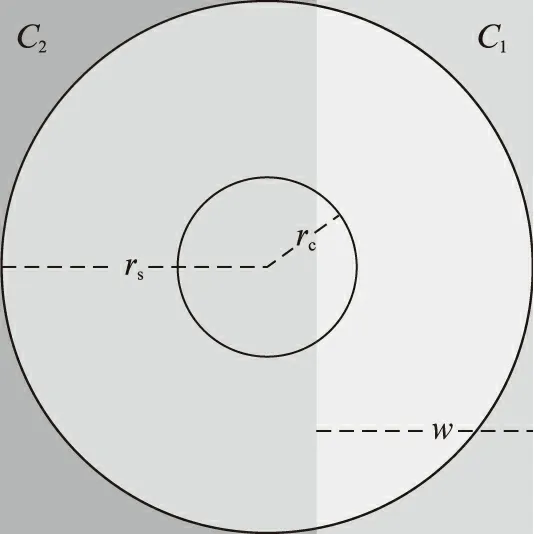
图1 对比刺激覆盖了一个神经元的同心圆式感受野Fig.1 Contrast stimulus covers the concentricreceptive field of a neuron

定义一个刻画感受野的重要参数——中心-周边半径比，即

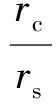
(1)

再定义一个参数用于描述构成边缘的刺激中较强刺激的近似比例，即

(2)

假定感受野内位于(x,y)的点接受到的刺激强度为h(x,y,η)。根据DOG模型[14]，此神经元对刺激的响应为

(3)

式中，σs、σc为参数，无特殊含义。

感受野是有限的区域而非整个二维平面。根据高斯函数的性质，应该有

(4)

(5)

以保证无穷积分和有限范围的二重积分近似相等。

本文根据边缘线在感受野中的不同相对位置，即η的不同取值范围化简上述积分。先简化构成边缘的刺激强度，不考虑c1和c2的具体数值，而只考虑两者的差值，即刺激的对比度。令对比刺激的刺激强度差Δ=c1-c2。

Θl=arccos(1-2η)

(6)

此时，可近似地将式(3)的二重积分化简为

(7)

Θs=arccos[(1>-2η)/rt]

(8)

此时，可近似地将式(3)化简为

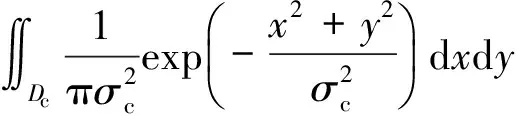
(9)

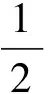
(10)

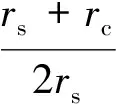
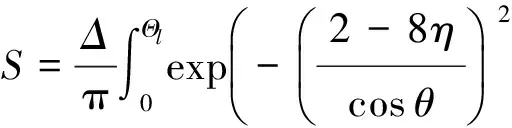
(11)

整理上述4种情况，记l=[(4-8n)/cosθ]2，可得到全部情况下的响应值表达式

S(Δ,η,rt)=

(12)

2 数学分析

虽然式(12)较为复杂，但通过简单地数学分析，本文能够得到LGN对边缘响应的一些特性。

(1) 函数S仅与Δ、η和rt有关。这反映了一个LGN细胞对比边缘的响应值只由3个因素决定，即该LGN细胞感受野的中心区和外周区半径比、构成边缘的刺激强度差、边缘落在感受野的相对位置。特别地，响应值与刺激的强度差为线性关系，无论两侧强度如何，响应值只与强度的差值成正比。

(2) 当0.5<η≤1时，S(η，rt)>0；反之，S(η,rt)≤0。这正表明，对于一个On型的LGN细胞，当刺激中的较强分量为主要成分时，它产生一个正反应；而当较弱分量为主要成分时，它产生一个负响应，此处正、负不是绝对意义，而表示被抑制的相对程度。对于Off型细胞，情况则刚好相反。

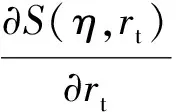
则同样能够证明Smax(rt)也是单调递减函数。这表明，随着rt的增加，归一化的最大响应值将下降。

(4) 给定η，归一化响应S只由rt控制。这表明，具有相近甚至相等的rt的神经节细胞可能具有相近甚至相同的响应特性。许多文献通过统计实验，如文献[15]中发现，对于LGN细胞，这一比值并无较大差异。

(5) 给定η和rt，响应值S只由Δ决定。大多数神经元都有一个产生神经脉冲的阈值，只有当刺激超出阈值需要的强度时，神经元才会输出响应值[16]。

3 实 验

虽然式(12)中仍较为复杂，但可以用数值计算的方式观测其性质。为进一步简化S，本文仅考虑Δ=1时的情况，令归一化的响应函数为

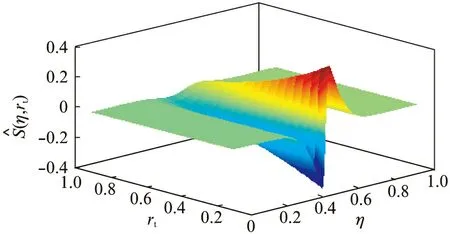
图2 rt∈(0, 1)和η∈[0, 1]时的响应曲面Fig.2 Response surface obtained withrt∈(0, 1) and η∈[0, 1]

4 结 语

本文根据经典的DOG模型设计了初级视觉通路中起中继作用的LGN细胞对边缘的响应模型。根据神经科学对视网膜上神经节细胞等细胞对刺激的响应特性的研究结果，本文用假设和简化，得到一个相对简单的归一化响应函数。此归一化响应函数只与刺激的对比边缘感受野中心点的相对位置，以及感受野的中心-周边半径比有关，而与刺激的对比度无关。若之后的任务可以在此基础上完成，则对方向的检测即可具有对比度不变性，从而可从一个方面解释视觉的对比度不变性。文献[18]中指出，归一化是脑功能的基础。本文得到的响应函数的曲线和生理学实验得到的曲线具有相似性，而在以往的研究中，此响应曲线的作用一直被忽略，后续研究工作将就这一曲线的可能作用，特别是在边缘检测中的作用进行深入讨论。

图3 rt=1/2,1/3,… ,1/9时的响应曲线Fig.3 Response curves obtained with rt=1/2,1/3,…,1/9

[1] Wei Y,Mel B.Possible role of convergent retinal inputs to LGN relay cells.Poster of Computational and Systems Neuroscience,2007: 179.

[2] Fukushima K.Neural network model for completing occluded contours.Neural Networks,2010,23(4): 528-540.

[3] Niu Wangqiang,Yuan Jingqi.Recurrent network simulations of two types of non-concentric retinal ganglion cells.Neurocomputing,2007,70(13/14/15): 2576-2580.

[4] Chirimuuta M,Gold I.The embedded neuron,the enactive field?∥Bickle J.The Oxford Handbook of Philosophy and Neuroscience.Oxford: Oxford University Press,2009: 200.

[5] Rodieck R W,Stone J.Analysis of receptive fields of cat retinal ganglion cells.Journal of Neurophysiology,1965,28(5): 833-849.

[6] Rodieck R W.Quantitative analysis of cat retinal ganglion cell response to visual stimuli.Vision Research,1965,5(12): 583-601.

[7] Kuffler S W. Discharge patterns and functional organization of mammalian retina. Journal of Neurophysiology, 1953,16(1): 37-68.

[8] Diedrich E,Schaeffel F.Spatial resolution,contrast sensitivity,and sensitivity to defocus of chicken retinal ganglion cells in vitro.Visual Neuroscience,2009,26(5/6): 467-476.

[9] Lee B B,Sun H.Contrast sensitivity and retinal ganglion cell responses in the primate.Psychology & Neuroscience,2011,4(1): 11-18.

[10] Enroth-Cugell C,Robson J G.The contrast sensitivity of retinal ganglion cells of the cat.Journal of Physiology-London,1966,187(3): 517-552.

[11] Gaudiano P.Simulations of X and Y retinal ganglion cell behavior with a nonlinear push-pull model of spatiotemporal retinal processing.Vision Research,1994,34(13): 1767-1784.

[12] Risner M L,Amthor F R,Gawne T J.The response dynamics of rabbit retinal ganglion cells to simulated blur.Visual Neuroscience,2010,27(1/2): 43-55.

[13] Schwartz G,Rieke F.Nonlinear spatial encoding by retinal ganglion cells: when 1+1≠2.The Journal of General Physiology,2011,138(3): 283-290.

[14] Einevoll G.Mathematical modelling in the early visual system: Why and how∥Buracas G,Ruksenas O,Albright T,et al.NATO Advanced Institute Series: Modulation of Neuronal Signaling: Implications for Visual Perception.Amsterdam: IOS Press,2003: 334.

[15] Kilavik B E,Silveira L C L,Kremers J.Centre and surround responses of marmoset lateral geniculate neurons at different temporal frequencies.The Journal of Physiology,2003,546(3): 903-919.

[16] Malmivuo J,Plonsey R.Bioelectromagnetism: Principles and Applications of Bioelectric and Biomagnetic Fields[M/OL].(2014-03-25).http:∥www.bem.fi/book/02/02.htm#05.

[17] Croner L J,Kaplan E.Receptive fields of P and M ganglion cells across the primate retina.Vision Research,1995,35(1): 7-24.

[18] Heeger D J.Normalization of cell responses in cat striate cortex.Visual Neuroscience,1992,9(2): 181-197.

Response of Lateral Geniculate Nucleus Cells to Edges

RENYuan

(School of Electronic Information Engineering, Shanghai Dianji University, Shanghai 200240, China)

Edges composing of stimuli of different intensities are common in both natural scenes and digital images. Edge detection is a basic step for machine visual systems, particularly machine biological visual systems. This paper establishes a model of lateral geniculate nucleus (LGN) cells in a primary visual pathway, describes the LGN cell response to edges, and provides feature representations for designing image processing approaches based on neural mechanism. According to physiological characteristics of retinal ganglion cells, the paper uses the classical model of difference of Gaussians to describe the LGN cell response to stimuli, and obtains a response function via reasonable simplifications. Through simple analyses, several mathematical properties of the response function are obtained, which agree with the physiological characteristics of neurons. By further simplifying the contrast of a stimulus, a normalized response function is obtained. Numeric experiments show that similarities exist between the function’s response curve and the physiological curve discovered in a previous neural science research, showing validity of the described model.

lateral geniculate nucleus (LGN); edge; receptive field; response curve; difference of Gaussians

2014 - 07 - 25

上海电机学院重点学科资助(13XKJ01-05)

任 远(1984-)，男，讲师，博士，主要研究方向为人工智能，E-mail: reny@sdju.edu.cn

2095 - 0020(2014)05 -0277 - 06

TP 3-05

A