带约束多设施选址分配模型与基于变分不等式的启发式算法

蒋建林, 程 坤

(南京航空航天大学 理学院,江苏 南京 210016)

0 引言

在现代物流系统中,设施选址是一个具有战略意义的课题,设施选址模型的研究与应用对现实生活有着重要而广泛的指导价值[1-7].韦伯问题(Weber problem,WP)[1]是设施选址领域的经典问题之一,它是指在平面上选择一个新设施,要求新设施到平面上已存在的m个需求点(顾客)间的欧几里得距离和达到最小.韦伯问题的模型是

(1)

其中ai是第i个需求点的已知位置,wi是第i个需求点的权重,m是需求点的数目,是新设施的未知位置,‖·‖2是l2范数.多设施选址问题(multi-source Weber problem,MWP)[2]是设施选址领域中另一个经典问题,其模型为

(2)

其中aj是第j个需求点的已知位置,xi表示第i个设施点的位置,sj表示第j个需求点的权重,sij表示第i个设施点服务第j个需求点的权重,m是待建的设施点的个数.

Weiszfeld算法[3]是求解单设施选址问题的经典算法,后又有改进的Weiszfeld算法[8]、Newton-Weiszfeld[5]等，均可以有效地求解WP.Cooper算法[2]是求解多设施选址问题的经典算法,分支定价算法[6]、Cooper-PC算法[7]等都可以有效地求解MWP.

1 模型的描述

考虑到实际生活中的设施之间会存在相互运输的情况,并且设施的选择也是有一定区域限制的,因此提出如下模型:

(3)

其中aj,xi,sij,sj与(2)是一致的,wij表示设施i与设施j的调运权重,Si为平面上的闭凸集,表示第i个设施的约束区域.在(3)中,‖·‖p表示lp范数(p≥1),是(1)和(2)中l2范数更一般的情形.称上述模型为约束多设施选址-分配模型,简称模型(3).

模型(3)与经典的多设施选址模型MWP主要不同在于:1) 该模型不仅考虑了各个设施点到相应的需求点之间的距离,还考虑到各个设施点之间的距离,目标是使得上述两个距离和最小;2) 该模型不再是考虑整个平面上的选址,而是对每个设施的选址区域进行约束,要求xi∈Si,i=1,2,…,m;3) 模型(3)使用了更一般的lp范数,这是因为在某些实际问题中,其它范数如l1和l∞范数,度量得到的距离更接近于真实值.以上3点考虑是符合实际生活的,因而约束多设施选址-分配模型具有更实际的应用背景.比如,如果计划新建m个工厂,这m个工厂不可能无限多地生产全部产品来满足市场需求,当某些工厂零部件或部分产品不能满足市场需求时,短期内无法足量生产,就需要向其邻近的工厂调集零部件或部分商品以满足市场需求.因此不仅要考虑设施点与需求点间的距离,还要考虑到设施点之间的距离.另外,在考虑到各方面的因素后,选址时往往对工厂位置有个预先的规划和限制,此时工厂的选址即为约束选址问题.此外,当在城市内进行选址时,用l1范数代替l2范数更能准确地度量城市内两点之间的距离.

模型(3)包含了设施选址领域中一些常见的经典模型:当i=1时,模型(3)就变成单设施韦伯问题(1);当wij=0(∀i,j)时,任何两个设施之间都不存在运输,模型(3)就是带约束的MWP;当wij=0(∀i,j)且Si=R2(i=1,2,…,m)时,模型(3)就是MWP(2).

注意到MWP(2)是非凸的[9]、NP难的[10]问题,求解此问题最重要的方法是Cooper算法.模型(3)作为MWP的推广问题,也是非凸的和NP难的.所以根据Cooper算法的思想,我们提出一种新的基于变分不等式的交替选址-分配启发式算法求解模型(3).

2 约束多设施选址分配模型的子问题求解

交替选址-分配启发式算法的特点是在算法执行过程中的每一步迭代都包括分配步和选址步.在分配步,根据设施点的位置,依据最近中心再分配算法进行需求点的分配,每个设施点服务的需求点组成了一个集合,称为分配簇.在选址阶段,根据当前的分配簇求解出新的设施点.交替选址-分配算法在需求点分配和设施选址之间不断交替,直到不需要再分配,也就是说,直到所有需求点都不需要从一个设施被分配到另一个设施.

2.1 分配步的最近中心再分配算法

最近中心再分配算法如下：

对于k=1,2,…,作如下运算:

Step 1 令t=0(t表示是否分配的标记).

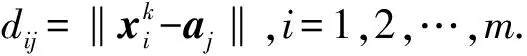
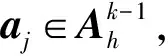
2.2 选址步的子问题求解

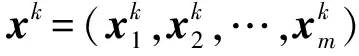
(4)

与模型(3)不同的是,CMLP(4)虽然也是一个多设施选址模型,但它是一个凸问题.对于CMLP的求解,我们的做法是先将其转化为单调的线性不等式问题,再运用投影收缩方法求得CMLP的最优解.

2.2.1 模型(4)与线性变分不等式(linearvariationalinequality,LVI)的关系

此节只详细介绍如何将l2范数下的CMLP问题转化为变分不等式问题,lp范数下的CMLP问题的转化与l2范数下的完全一样,因此略去.对于任意的d∈R2,有

(5)

利用(5),上述l2范数意义下的最短距离和问题(4)可以化为min-max问题

(6)

写成紧凑形式为

(7)

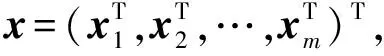
X=S1×S2×…×Sm,

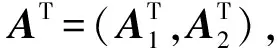
aT=(a11,a12,…,a1n1,a21,a22,…,a2n2,…,am1,am2,…,amnm,0,0,…,0).

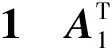
zT(Ax*-a)≤z*T(Ax*-a)≤z*T(Ax-a).

(8)

它的等价形式是下面的线性变分不等式：

(9)

可以写成更为简单紧凑的形式

u*∈Ω, (u-u*)T(Mu*+q)≥0, ∀u∈Ω,

(10)

其中

(11)

因为问题(10)～(11)中的矩阵M有MT=-M,因此M是半正定的矩阵.

性质1(4)等价于LVI(10),即它们具有相同的xi,i=1,2,…,m.

证因为(4)等价于(6),所以只需证明(6)等价于LVI(10).下面证明(x*,z*)是(6)的解当且仅当(x*,z*)是LVI(10)的解.

设(x*,z*)是(6)的解,根据上述推理过程,易得(x*,z*)是LVI(10)的解.

再设(x*,z*)是LVI(10)的解

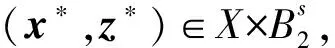
(12)

即

(13)

(14)

(15)

比较(13)和(15)式,可以得到(13)中所有式子全部相等,所以

(16)

由此可知(x*,z*)是(6)的解.命题得证.

2.2.2 求解LVI问题(10)的投影收缩方法

求解LVI问题(10)有很多种方法,投影收缩方法[7,12]是其中非常实用简单的一种方法.本文中我们将用He[12]的投影收缩方法求解LVI(10).设Ω是Rn中的非空闭凸集,M是Rn×n的半正定矩阵,q∈Rn.变分不等式问题就是在Ω中确定u*,使得u*∈Ω,(u-u*)T(Mu*+q)≥0, ∀u∈Ω.变分不等式问题等价于求解e(u)=u-PΩ(u-(Mu+q))=0,所以变分不等式问题的求解中经常用‖e(u)‖≤ε作为数值算法的迭代终止准则.

投影收缩(projection-contraction,PC)方法如下：

Step 0 设Δ1和Δ2是两个确定的常数，满足0<Δ1<Δ2<2.给定ε>0和初始解u0∈Ω.令k=0.

Step 1 计算e(uk)=uk-PΩ(uk-(Muk+q)).如果‖e(uk)‖∞≤ε,停止.

性质2设u*是LVI(10)的解,令u0∈Ω是LVI(10)的初始解,那么对LVI(10)经投影收缩方法所产生的迭代序列{uk}满足

(17)

具体的证明过程可参见文献[12].

由性质2可知,‖e(uk)‖→0,因此PC方法得到的迭代序列{uk}是收敛的且收敛于u*.

3 基于变分不等式的交替选址分配启发式算法

基于变分不等式的交替选址-分配启发式算法如下：

Step 0 令t=0(t表示是否分配的标记),k=1.

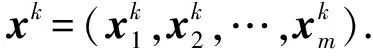
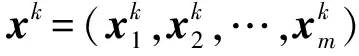
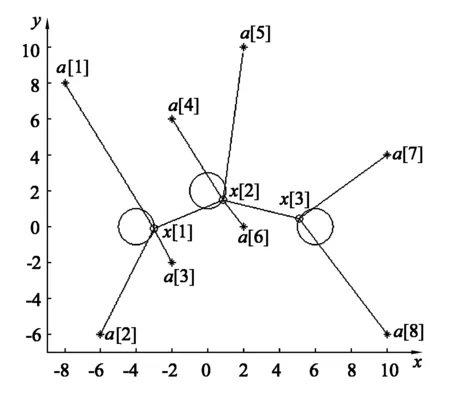
性质3设x0是初始解,A0是由x0产生的分配簇,如果xk+1≠xk,则由(x0,A0)产生的迭代序列C(x0,A0)是严格单调递减的,即C(xk+1,Ak+1)

C(xk+1,Ak)

(18)

另一方面,因为在分配阶段中实行最近中心再分配算法,因此

C(xk+1,Ak+1)≤C(xk+1,Ak).

(19)

结合(18)和(19),得到C(xk+1,Ak+1)

由于模型(3)是非凸的和NP难的,因此求解模型的全局最优解非常困难且难以实现.注意到对于子问题CMLP的求解我们是将其转化为等价的变分不等式问题,并通过PC方法求得CMLP的最优解,因此根据交替选址-分配算法的思想[2],基于变分不等式的交替选址-分配启发式算法与Cooper算法求解MWP一样将会得到模型(3)的局部最优解．

4 数值实验

通过两个数值例子来说明基于变分不等式的交替选址-分配启发式算法的有效性.第一个例子是参考文献[2],选取此例说明该算法可以解决一般的无约束多设施选址问题MWP(2),多设施选址问题是快速且有效的.第二个例子是考虑设施之间存在相互运输的情况以及带约束的情形,以此来说明该算法可以用于求解更实际的约束多设施选址-分配模型.所有的程序均用Matlab 2012b编写,在P4 2G的笔记本上运行,迭代中止准则为PC方法常用准则

e(u)=u-PΩ(u-(Mu+q))≤10-5.

图1 需求点和设施点的坐标位置

例1选取15个需求点,权重全为1,文献[2]报告的设施解为{(8.888,14.466),(20.997,44.998),(40.361,17.968)},函数值为143.209.运行本文算法得到的设施解为{(8.947,14.637),(21.000,45.000),(40.042,17.493)},函数值为143.196 3,运行时间为0.116 13秒.

上述两解对比即可看出,本文得到的解比文献[2]略优,可见，此算法对解决多设施选址问题是有效的.

例2在问题(3)中选取8个需求点,分别为{(-8,8),(-6,-6),(-2,-2),(-2,6),(2,10),(2,0),(10,4),(10,-6)},目标是建立3个设施点,限制中心分别为(-4,0),(0,2),(6,0),限制区域为单位圆,需求点的权重sj全部取为1,设施点的运输权重为w12=2,w13=0,w23=2,应用我们的算法运算后得到设施解为(-3.006 8,-0.116 6),(-0.853 0,1.478 1),(5.104 9,0.445 9),函数值为65.329,运行时间为0.006 15秒.需求点和设施点的位置关系见图1.

由此可见,我们提出的基于变分不等式的启发式算法求解更实际的约束多设施选址-分配模型也是快速有效的.

本文主要研究了一种约束多设施的最小距离和问题:在平面上的一些闭凸集中寻找最优位置建立多个设施,使得新设施到其服务的需求点距离和以及各设施之间的距离和达到最小.本文提出的模型更接近于实际运用.

参考文献:

[1] Weber A.Über den standort der industrien[M].Paul Siebeck:JCB Mohr,1909.

[2] Cooper L.Heuristic methods for location-allocation problems[J].Siam Rev,1964,6(1):37.

[3] Weiszfeld E.Sur le point pour lequal la somme des distance denpoints donnés est minimum[J].Tohoku Math J,1937,43(2):355.

[4] Love R F,Morris J G.Mathematical models of road travel distance[J].Manag Sci,1979,25(2):130.

[5] Jiang Jianlin,Cheng Kun,Wang Cancan,et al.Accelerating the convergence in the single-source and multi-source Weber problems[J].Appl Math Comput,2012,218(12):6814.

[6] Righini G,Zaniboni L.A branch-and-price algorithm for the multi-source Weber problem[J].Int J Oper Res,2007,2(2):188.

[7] Jiang Jianlin,Yuan Xiaoming.A heuristic algorithm for constrained multi-source Weber problem—the variational inequality approach[J].European J Oper Res,2008,187(2):357.

[8] Vardi Y,Zhang Cunhui.A modified Weiszfeld algorithm for the Fermat-Weber location problem[J].Math Program,2001,90(3):559.

[9] Cooper L.Solutions of generalized equilibrium models[J].J Region Sci,1967,7(1):1.

[10] Megiddo N,Supowit K J.On the complexity of some common geometric location problems[J].SIAM J comput,1984,13(1):182.

[11] Brimberg J,Walker J H,Love R F.Estimation of travel distances with the weightedlpnorm:some empirical results[J].J Transport Geog,2007,15(1):62.

[12] He B S.A modified and projection and contraction method for a class of linear complementarity problems[J].J Comput Math,1996,14(1):54.