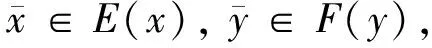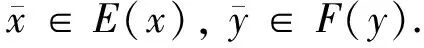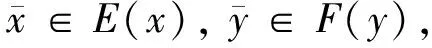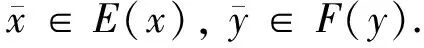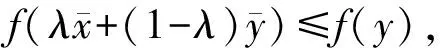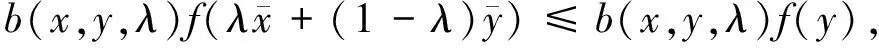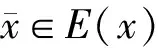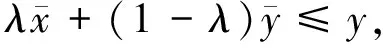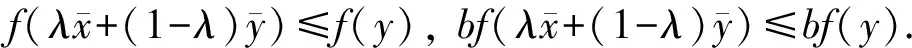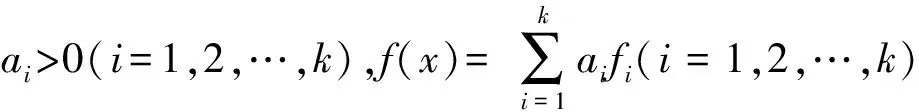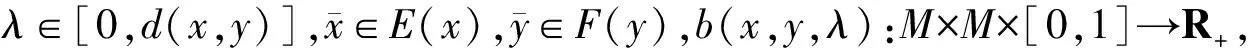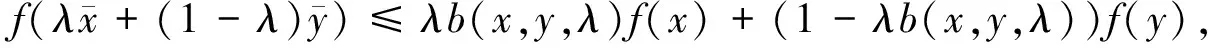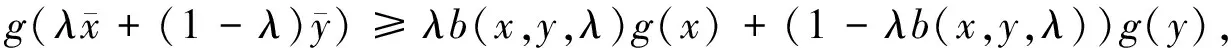半局部B半(E,F)凸函数及其性质

高 晔, 张庆祥, 邢 苗

(延安大学 数学与计算机科学学院,陕西 延安 716000)

0 引言

凸集与凸函数在最优化理论中有着广泛的应用,但实际问题中大量集合与函数是非凸的,因此有必要对它们进行推广.Youness[1]通过弱化凸集与凸函数的条件给出了E凸集、E凸函数等概念,并得出了相关结论.虽然有些结论不正确,但其思想意义是不容质疑的.为此，杨新民、简金宝、覃义先后指出和修正了关于E凸集、E凸函数及E凸规划的几个错误[2-4].Ewing[5],Weir[6]分别引入了局部凸函数、半局部凸函数的概念.简金宝等研究了广义半局部凸函数及其性质[7].胡清洁等给出了半局部E凸函数的概念,并讨论了它的性质[8].2009年，简金宝给出了(E,F)凸集、(E,F)凸函数的概念[9],之后，简金宝、路敏慧等[10-11]研究了它们的性质.2004年，简金宝等在文献[12]中引入了半(E,F)凸函数及其规划问题,张庆祥等对拟半(E,F)预不变凸函数进行了研究[13],并探讨了广义凸函数的半无限规划对偶问题[14]，曾友芳等探究了B半(E,F)凸函数和规划[15].在文献[16]中，Tang引入了局部星形集,并在星形集的基础上定义了半局部凸函数.在这些理论的基础上，高晔等人提出了半局部半(E,F)凸函数,并研究了其性质[17].

本文在局部星形(E,F)凸集、半局部凸函数和B半(E,F)凸函数基础上,定义半局部B半(E,F)凸函数及几类广义半局部B半(E,F)凸函数,并研究它们的性质，以及与某些广义凸函数之间的关系.

1 预备知识

定义1[17]设x0∈M⊆Rn,若映射E,F:M→2Rn,对每个x∈M,都存在正数α(x0,x)≤1,且对∀λ∈(0,α(x0,x)),有λE(x0)+(1-λ)F(x)⊆M,则称M在点x0处为局部星形(E,F)凸的.若M在每个x0∈M处是局部星形(E,F)凸的,则称M为局部星形(E,F)凸集.

定义2[16]函数f:M→R为M上的B半(E,F)凸函数,若存在两个点到集合的映射E,F:M→2Rn和函数b(x,y,λ):M×M×[0,1]→R+,使得M是(E,F)凸集且∅≠M⊆Rn,有

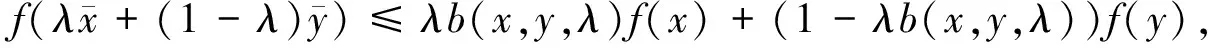
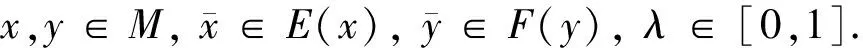
定义3[15]函数f:M→R为M上的拟B半(E,F)凸函数,若存在两个点到集合的映射E,F:M→2Rn和函数b(x,y,λ):M×M×[0,1]→R+,使得M是(E,F)凸集且∅≠M⊆Rn,有

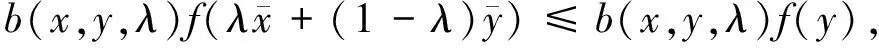
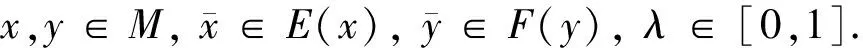
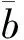
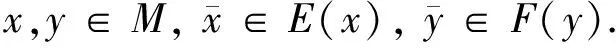
定义5[16]设f(x)为局部星形集M⊆Rn上的实值函数,若对∀x,y∈M,存在正数d(x,y)≤α(x,y)≤1,使得对∀λ∈(0,d(x,y)),有

f(λx+(1-λ)y)≤λf(x)+(1-λ)f(y),

则称f(x)为M上的半局部凸函数.

2 半局部B半(E,F)凸函数

定义6函数f:M→R为M上的半局部B半(E,F)凸函数,若存在点到集合的映射E,F:M→2Rn,正数d(x,y)≤α(x,y)≤1和函数b(x,y,λ):M×M×[0,1]→R+,使得M是局部星形(E,F)凸集且∅≠M⊆Rn,有

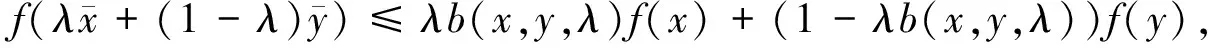
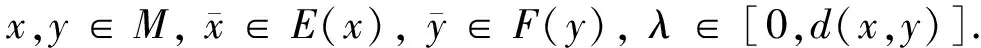
定义7设函数f为M上的实值函数,若存在点到集合的映射E,F:M→2Rn,正数d(x,y)≤α(x,y)≤1和函数b(x,y,λ):M×M×[0,1]→R+,使得M是局部星形(E,F)凸集且∅≠M⊆Rn,那么

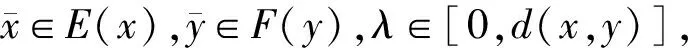
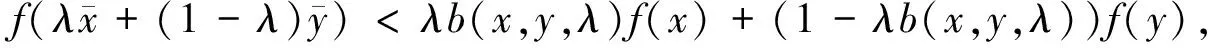
(1)

则称f是半局部B半(E,F)严格凸函数.

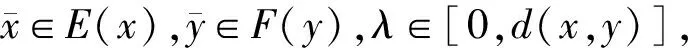
定义8函数f:M→R为M上的半局部B半(E,F)拟凸函数,若存在两个点到集合的映射E,F:M→2Rn，正数d(x,y)≤α(x,y)≤1和函数b(x,y,λ):M×M×[0,1]→R+,使得M是(E,F)凸集且∅≠M⊆Rn,有

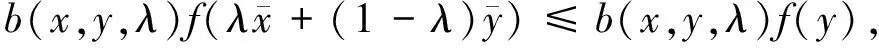
(2)

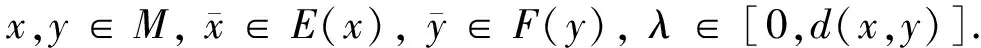
定义9设函数f为M上的实值函数,若存在点到集合的映射E,F:M→2Rn,正数d(x,y)≤α(x,y)≤1和函数b(x,y,λ):M×M×[0,1]→R+,使得M是局部星形(E,F)凸集且∅≠M⊆Rn,那么

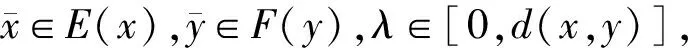
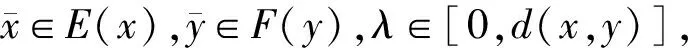
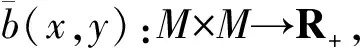
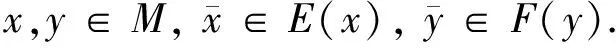
定义11设函数f为M上的半局部B半(E,F)伪拟凸函数,若存在点到集合的映射E,F:M→2Rn,正数d(x,y)≤α(x,y)≤1和函数b(x,y,λ):M×M×[0,1]→R+,使得M是局部星形(E,F)凸集且∅≠M⊆Rn,有

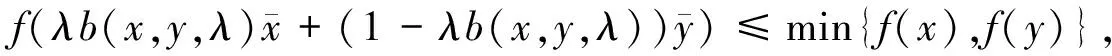
3 半局部B半(E,F)凸函数的性质

性质1设f:M→R为定义在局部星形(E,F)凸集M⊆Rn上的半局部B半(E,F)凸函数,则对任意κ∈R,水平集Sκ={x|x∈M,f(x)≤κ}为局部星形(E,F)凸集.

≤λb(x,y,λ)κ+(1-λb(x,y,λ))κ

=κ,

即对任意0<λ

性质21) 当映射E,F为恒等映射,即E(x)={x},E(y)={y},d(x,y)=1时,半局部B半(E,F)凸函数为B凸函数.

2) 当b(x,y,λ)≡1且满足1)时,半局部B半(E,F)凸函数即为熟知的凸函数.

因此由定义知f是半局部B半(E,F)凸函数.

注1性质3的逆命题不成立.

例1设f:M=[-1,1]→R,E,F:M→2R和b:X×X×[0,1]→R+为

显然M为局部星形(E,F)凸集.下面验证f是M上的半局部B半(E,F)凸函数.

首先,假设x

当y∈[0,1]时,有

当x∈[0,1]时,有

性质4若f(x)为半局部B半(E,F)凸函数,则它也是半局部B半(E,F)拟凸函数.

由定义8可知,f是半局部B半(E,F)拟凸函数.

注2性质4的逆命题不成立.

例2设f:M=[0,1]→R,E,F:M→2R和b:X×X×[0,1]→R+为

显然M为局部星形(E,F)凸集.下面验证f是M上的半局部B半(E,F)拟凸函数.假设f(x)≤f(y).

∀λ∈(0,d],d(x,y)∈(0,1],

性质5若f是半局部B半(E,F)凸函数，则

1) 对∀a∈R,f+a也是M上的半局部B半(E,F)凸函数;

2) 对∀a∈R,af也是M上的半局部B半(E,F)凸函数;

3) 对于M上的另一半局部B半(E,F)凸函数g,f+g也是M上的半局部B半(E,F)凸函数.

性质6若函数f为局部(E,F)凸集M上的半局部B半(E,F)凸函数,φ:R→R是非减凸函数,则复合函数φ(f)是M上的半局部B半(E,F)凸函数.

又φ:R→R为非减凸函数,所以

≤λb(x,y,λ)φ(f(x))+(1-λb(x,y,λ))φ(f(y)),

所以,复合函数φ(f)是M上的半局部B半(E,F)凸函数.

性质7设f(x)为定义在局部星形(E,F)凸集M⊆Rn上的半局部B半(E,F)拟凸函数,若φ:R→R为非减的函数,则φ(f(x))也为半局部B半(E,F)拟凸函数.

性质8设f,-g:M→R是局部星形(E,F)凸集M上的半局部B半(E,F)凸函数,若f≥0,g>0,则h=f/g是M上的半局部B半(E,F)拟凸函数.

则

≤max{h(x),h(y)}.

当h(x)≤h(y)时,上式两边同乘以b(x,y,λ),即得

因此,函数h=f/g是M上的半局部B半(E,F)拟凸函数.

参考文献:

[1] Youness E A.E-convex sets,E-convex functions andE-convex programming[J].J Optim Theory Appl,1999,102(2):439.

[2] Yang Xinmin.Technical note onE-convex set,E-convex functions,andE-convex programming[J].J Optim Theory Appl,2001,109(3):699.

[3] Jian Jinbao.Incorrect results forE-convex functions andE-convex programming[J].J Math Res Expostion,2003,23(3):461.

[4] 覃义,简金宝.关于E凸函数及E凸规划几个错误结论的修正[J].数学杂志,2006,26(2):177.

[5] Ewing G M.Sufficient conditions for global minima of suitably convex functionals from variational and control theory[J].SIAM Rev,1977,19(2):202.

[6] Weir T.Programming with semilocally convex functions[J].J Math Anal Appl,1992,168(1):1.

[7] Jian Jinbao,Pan Huaqin,Zeng Hanjun.Semilocally prequasi-invex functions and characterizations[J].J Ind Manag Optim,2007,3(3):503.

[8] Hu Qingjie,Jian Jinbao,Zheng Haiyan,et al.SemilocalE-convexity and semilocalE-convex programming[J].Bull Austral Math Soc,2007,75(1):59.

[9] Jian Jinbao.On (E,F) generalized convexity[J].Int J Math Sci,2009,2(1):121.

[10] Jian Jinbao,Hu Qingjuan,Ma Pengfei,et al.On properties of quasi-semi-(E,F)-convex functions and quasi-semi-(E,F)-convex programming[J].Oper Res Trans,2012,16(1):49.

[11] 路敏慧,于宪伟.(E,F)凸集,(E,F)凸函数的一些新性质[J].渤海大学学报:自然科学版,2010,31(1):52.

[12] Jian Jinbao,Hu Qingjie,Tang Chunming,et al.Semi-(E,F)-convex functions and semi-(E,F)-convex programming[J].Int J Pure Appl Math,2004,14(3):439.

[13] 张庆祥,邢苗,高晔.拟半(E,F)预不变凸函数及其性质[J].江苏师范大学学报:自然科学版,2013,31(2):17.

[14] 张庆祥,赵丽丽,王建明,等.广义K-(F,α,ρ,d)-B凸半无限多目标规划的Wolfe型对偶问题[J].江苏师范大学学报:自然科学版,2012,30(4):38.

[15] 曾友芳,简金宝,晁绵涛.B-半-(E,F)-凸函数和规划[J].运筹学学报,2009,13(2):68.

[16] Tang Huanwen,Jiang Ye,Guo Jian,et al.Fixed point algorithms and its application to nondifferentiable programming approximization:optimization and computing[M].Amsterdam:Elsevier Science Publishers,1990:291-294.

[17] 高晔，张庆祥，邢苗.半局部半(E,F)-凸函数及其性质[J].江西师范大学学报：自然科学版，2014,38(1):59.