基于弹性变形的机床主轴参数设计方法研究
2014-09-13安虎平张志梅杨天兴刘昊王玲
安虎平,张志梅,杨天兴,刘昊,王玲
(1.兰州城市学院机械检测与故障诊断研究所,甘肃兰州730070;2.兰州交通大学后勤集团公司,甘肃兰州730070)
机床主轴是实现切削主运动的执行部件,在切削系统中起关键作用。在机械制造装备设计中,主轴设计合理性关系到机床性价比优劣,主轴精度在很大程度上决定了机床工作精度。在传动系统确定的情况下,主轴支承结构的配置是影响主轴刚性、工作精度、结构、体积及成本的重要因素。如CW6163系列车床经过多年生产、改进设计,其结构趋于完善,品种规格日益齐全,生产工艺基本稳定。我国生产企业基于其局部结构和外观的不足进行改进设计、增加品种规格,满足了不同行业生产需要。然而,该机床精度还不够高,其主要原因是生产商对主轴支承的合理性缺乏理论分析和技术手段。从实际生产经验获知,要想进一步提高机床工作精度,难度较大,因为设计部门已经试用过多种类型主轴支承轴承及其预紧结构,效果不明显。此外,该机床的数控化改造不够理想,其中原因之一就是精度与数控系统匹配度不高,只限于简易型数控。鉴于多年制造装备设计制造经验和力学研究的体会,作者认为有必要对机床主轴支承的力学性能进行分析,利用现代数值分析软件MATLAB描绘,充分认识影响主轴精度的主要因素,为主轴参数设计提供依据。
1 主轴技术要求与标注
为保证机床主轴有足够精度和良好的工作稳定性,在设计阶段应对主轴结构各部位(特别是轴承、夹具、传动件、连接件与预紧件的安装部位)提出适当的技术条件,包括尺寸公差、形位公差、表面粗糙度和表面硬度等,并在主轴零件图上合理标注。这些技术条件应满足下列要求:1)设计要求:要满足机床工作性能对主轴精度、噪声和其他技术指标的规定;2)工艺要求:在满足设计要求的前提下,须充分考虑制造的可能性和经济性,使设计合理,为此应尽量使工艺基准与设计基准统一;3)检测要求:即采用简便、准确而可靠的测量手段,尽量做到使检验基准与工艺基准一致;4)标注要求:要采用规范的标注代号完整地标注出检测位置和检测项目要求,如有特殊要求而无法用代号标注时,要用简练准确的文字在技术要求或图上标注处说明。如图1所示,为一主轴公差标注示意图,轴颈A、B处的公共轴心线A-B是保证主轴旋转精度的设计基准,同时也是法兰前端面、主轴头短锥和内锥孔的工艺基准及检验基准,因此轴颈精度与表面粗糙度应严格控制。轴颈尺寸公差应根据与之相配轴承类型选取,同轴度可通过轴颈表面的径向圆跳动公差来控制,该方法的误差测量方便。主轴短锥面是安装卡盘的定心面,直接影响加工精度,其结构和参数设计须遵循相应的主轴头标准;内锥孔是安装主轴顶尖的基准面,应保证与轴颈中心线同轴度要求,加工时以轴颈为基准面精磨锥孔,用标准检验棒和千分表按图样规定及相关机床标准检测,其检测结果须符合相应机床精度标准规定;轴颈表面是主轴与齿轮及其他配合件表面位置度的测量基准,如图1中Ⅰ~Ⅳ处。普通机床的轴颈尺寸取IT5级精度[1],形状公差值取尺寸公差值的1/4~1/3,安装齿轮配合表面的跳动公差可略小于其直径公差的1/2。

图1 主轴公差标注示意图
2 主轴组件计算模型
由图1可知,机床主轴结构比较复杂,刚度和精度是主轴技术要求的主要内容。满足刚度要求的结构设计应首先从受力变形角度进行分析计算来决定其主要结构尺寸,这些尺寸参数有主轴前后支承轴颈尺寸D1、D2,主轴内孔直径d,主轴支承跨距l和前端悬伸量a等,这些参数直接影响主轴的刚性和工作精度。
机床主轴所受的工作载荷为动载荷,包括扭矩和切削力。对于回转类切削机床,主轴扭转变形小,对加工精度的影响不大,而由切削力引起的径向载荷对主轴系统的刚度和精度影响最大。因此以径向载荷来分析主轴受力变形,以确定合理的主轴结构参数。根据主轴结构和受力特点,用材料力学理论分析并对主轴部件支承按静力状态进行简化,建立其受力模型,如图2所示。主轴工作时带动工件或刀具作主运动,受切刀具削作用产生切削扭矩和径向力。扭矩使主轴产生扭转变形;径向力使主轴发生弯曲变形,并引起主轴前端变形位移δs;同时主轴支承件—轴承和箱体等受切削力和部件重力作用也会发生弹性变形,从而引起主轴前端发生位移δz,因此,主轴前端的总位移δ应等于这两种位移的叠加。考虑到主轴和支承件都是变形体,对双支承主轴的受力模型可表示为如图2(a)所示的外伸简支梁形式,其中Fc是主轴所受的径向载荷;RA为前支承反力;RB为后支承反力。为便于分析计算,图2(a)可看作弹性主轴-刚性支承与刚性主轴-弹性支承两种情况的叠加,分别如图2(b)与图2(c)所示。

图2 主轴部件受力变形简化模型
2.1 主轴轴颈尺寸的确定
主轴直径大小与主轴部件的刚度有关,会影响机床加工精度。由材料力学[2]可知,外伸梁的刚度可表示为:

式中:K—主轴刚度,(N/μm);
E—主轴材料弹性模量,(GPa);
I—截面惯性矩,(mm4);
l—支承跨距,(mm);
a—悬伸量,(mm)。
由式(1)可知,主轴刚度随跨距和悬伸量的增大而非线性减小,与主轴材料弹性模量和截面惯性矩成正比,而惯性矩与直径的四次方成正比,即主轴刚度与直径的四次方成正比关系。对于确定的主轴材料和传动系统来说,增大主轴直径可提高主轴刚度和系统抗振性,但主轴直径过大会带来一系列问题:1)使安装于主轴上零部件尺寸增大,造成结构庞大;2)增加制造成本,主轴、传动件、支承件和箱体等尺寸及误差和变形随之增大,增加了制造难度,从而使制造成本大幅度增加;3)空载功率增大,传动件质量加大意味着空载功率消耗加大;4)轴承速度参数限制,主轴轴径大小受轴承允许速度参数d·nmax的限制。

表1 主轴前轴径D1的选择
主轴前轴颈D1可根据机床传递功率并参考同类机床轴颈尺寸加以确定,如表1所示,为最典型两类机床主轴前轴颈D1的参考值。因装配工艺需要,主轴直径自前向后是逐步减少的,主轴后轴颈D2与前轴颈D1的关系,可按经验公式D2=(0.7~0.9)D1初选,再结合结构设计来最终确定。
2.2 主轴内孔直径的确定
机床主轴一般具有内通孔,可减轻质量并用于穿越棒料、安装刀具和工具。根据材料力学理论,在一定范围内主轴内孔对强度和刚度影响很小,但若超过此范围则会使主轴强度与刚度急剧下降。从结构和工艺上考虑,主轴内孔直径受后轴颈尺寸限制,其大小应从刚度和强度两个方面分析决定。
1)内孔直径的刚度确定法 由式(1)可知,轴刚度正K比于截面惯性矩I,空心轴截面形心的惯性矩Ih=π(D4-d4)/64,实心轴的惯性矩Is=πD4/64,则空心轴与实心轴刚度比值为:
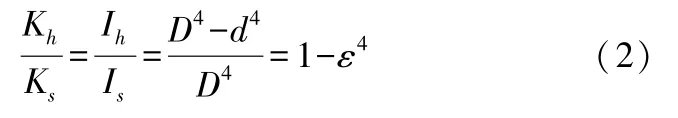
式中:Kh,Ks—分别为空心和实心轴的刚度,(N/μm);
Ih,Is—分别为空心和实心轴截面惯性矩,(mm4);
D—主轴平均外径,(mm);
d—主轴内径,(mm);
ε—刚度衰减系数,ε=d/D。
如图3所示,为用MATLAB软件得到的空心轴与实心轴刚度及强度随ε衰减情况。由式(2)及图3可知,当ε=0.5时,Kh/Ks=0.937 5;当ε=0.7 时,Kh/Ks=0.759 9。即当ε较小时,空心轴刚度衰减很小;当ε较大时,空心轴刚度衰减较大。因此,为保证主轴足够的刚度,通常应取ε≤0.7。实际设计时,可根据主轴刚度和精度要求确定刚度衰减系数,当刚度要求较高时,ε取较小值;反之,可取较大值。当确定了刚度衰减系数后,即可根据外径D与ε来确定内孔直径d,然后再按用途来确定主轴前端锥孔的锥度。当只用于定心时,锥孔锥度取较大值;当要求定心并能自锁时,锥孔锥度应取较小值。
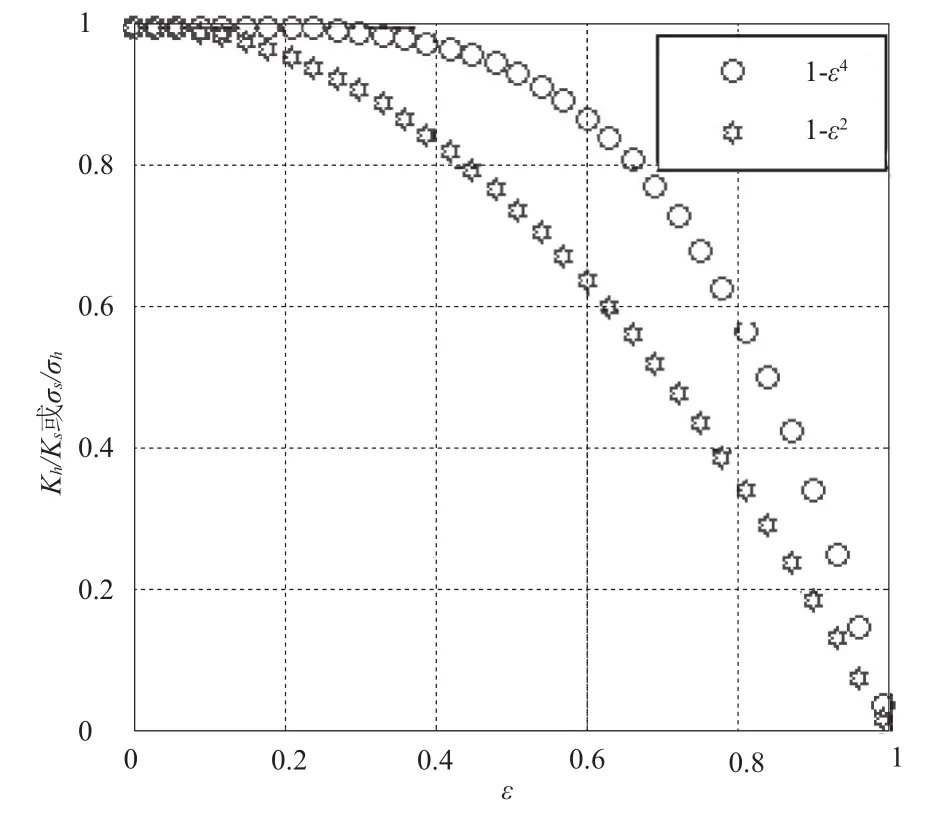
图3 主轴强度和刚度与内外径之比
2)内孔直径的强度确定法 对于实心轴,强度为σs=4F/πD2≤[σ];对于空心轴,强度为σh=4F/π(D2-d2)≤[σ],则空心轴与实心轴强度的关系为:
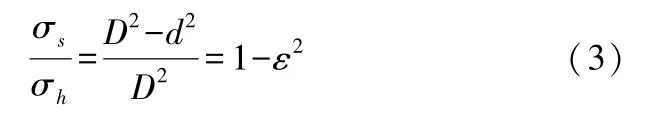
式中:σs—实心轴应力,(MPa);
σh—空心轴应力,(MPa)。
由式(3)可知,随刚度衰减系数ε增大(即内径增大),空心轴应力增大,主轴强度降低。图3表明,随内径增大,主轴强度比刚度衰减更快,当ε=0.5时,空心轴强度是实心轴的75%。
当设计主轴时,应兼顾强度和刚度。强度主要根据传递功率和扭矩及转速来确定,通常主轴设计强度是足够的,主要应考虑精度问题。在满足通孔使用要求的前提下,应取较小的ε值,这样可使获得较高的强度和刚度值,有利于提高精度。
2.3 主轴最佳跨距和悬伸量
主轴跨距是指其前-后或前-中支承反力作用点之间的距离;悬伸量是指主轴头部安装夹具的定位基面至前支承径向反力作用点之间的距离。跨距和悬伸量对主轴组件刚度有直接影响。由前面主轴力学模型可知,主轴组件的刚度取决于主轴自身刚度和支承刚度。在弹性限度内,可将图2(a)分解为下列两种情况来讨论。
1)刚性支承与弹性主轴 如图2(b)所示,不考虑支承点变形位移,仅由主轴弯曲引起的悬臂端挠度为:

式中:δs—弹性主轴悬臂端的挠度,(μm);
Fc—主轴端部所受的径向载荷,(N);
I—主轴截面的平均惯性矩,(mm4),当主轴平均直径为D,内孔直径为d时,I=π(D4-d4)/64。由主轴弹性弯曲引起的柔度为:

由式(5)可知,当其他条件一定时,柔度δs/Fc与跨距成线性关系,如图4中的直线所示。

图4 轴端位移与主轴跨距的关系
2)弹性支承与刚性主轴 如图2(c)所示,设前后支承的刚度分别为KA、KB,变形量分别为δA、δB,则有δA=RA/KA,δB=RB/KB。 其中:RA,RB—分别为前、后轴颈的支反力(N),RA=Fc·(1+a/l),RB=Fc·a/l。 根据变形几何关系,得(δA+δB)/l=(δz+δB)/(l+a),则由支承变形引起主轴前端位移为:

式中:δz—由支承变形引起的主轴前端位移,(μm)。第一项表示前支承的影响;第二项表示后支承的影响。则由支承位移引起主轴的柔度为:

式中:δz/Fc—主轴柔度(μm/N)。 由于一般a<l,由(6)式可知前支承对主轴端变形的影响比后支承大。所以在主轴部件设计时,前轴承应取较大刚度值,后轴承可取较小刚度值;前轴承精度应比后轴承高一级。
3)主轴端部实际位移 实际受力后,主轴和支承同时产生变形,故应综合考虑这两种变形引起的总位移,按弹性变形考虑,有:
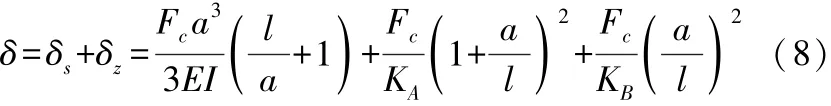
式中:δ—为主轴端部总位移,(μm)。
从式(8)可知,总位移与主轴及前、后支承的变形有关,后支承影响最小。主轴端部总柔度为:

式中:δ/Fc—主轴前端总柔度(μm/N)。
以CW6163车床主轴为例,有关参数如表2所示。主轴前端柔度与跨距关系如图4所示,在主轴前端悬伸量a一定时,随前后支承跨距l增大,主轴前端位移δ先减小;大约在l/a=0.8时,达到最小,尔后近似成直线增大。

表2 主轴组件有关参数
4)主轴最佳跨距的确定 主轴最佳跨距是指使主轴柔度最小(刚度最大)的跨距。在式(8)中,令dδ/dl=0,得a2/(3EI)-2a2(1/KA-1/KB)/l3-2a/(KAl2)=0。整理,得到关于l的一元三次方程:
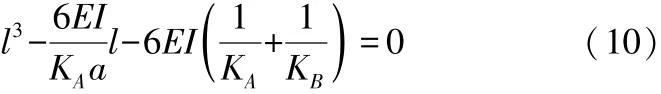
取综合变量η=EI/(KAa3),代入式(10),得:

式(11)中,无量纲量η是l/a和KA/KB的函数,以KA/KB为参变量,以l/a为变量,利用 MATLAB计算软件编程[3-4],做η的计算线图,如图5所示。
图5中分别给出了主轴前后支承刚度比KA/KB取值为1、2、3、4、5时,综合变量η的五条曲线。 显然该图更精确地给出了主轴最佳跨距的计算线图曲线。当a值给定时,存在一最佳跨距l0,通常取l0/a=2~3.5。

图5 主轴最佳跨距计算线图
3 计算示例
某一回转直径400 mm的普通车床,电机功率为7.5 kW,主轴内孔直径为52 mm,主轴前后支承均为NN 3 000 K系列双列圆柱滚子轴承,主轴计算转速为50 r/min。试初选主轴轴颈跨距。
根据表 1,取前轴颈为 110~145 mm,初定D1=120 mm,后轴颈D2=0.75D1=90 mm。按结构,定悬伸长a=120 mm。
1)轴承刚度计算 主轴最大输出转矩:
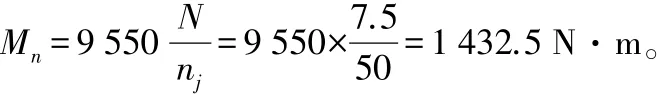
床身上最大加工直径约为最大回转直径的60%,即240 mm,最大加工半径为120 mm。主切削力和切深抗力分别为:

总切削力
估算时,先取初值l/a=3,即l=3a=360 mm。假设切削力是作用于前后两顶尖之间工件上,主轴和尾座各承担一半,则前、后支反力分别为:
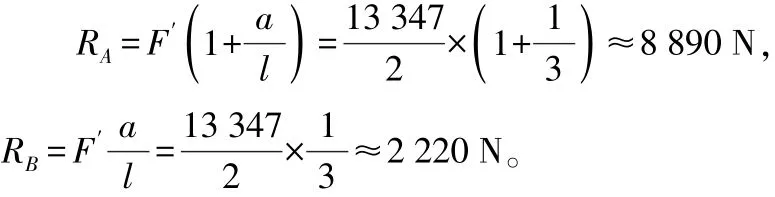
根据轴承刚度验算公式可求得前后轴承的刚度为:

2)求最佳跨距,取主轴的当量外径为前后轴颈的平均值,即×(120+90)=105 mm,故惯性矩I=(0.1054-0.0524)/64=178.4×10-8m4,则:

查图5,得l0/a=1.6,这一值与假设值不符,可根据l0/a=1.6重新计算支反力和支承刚度,再求最佳跨距,如此反复迭代,直到与假设值接近为止,可求得合理的跨距。
4 结语
针对机床主轴组件设计的难点问题进行研究,内容有:1)给出主轴设计的主要技术要求和标注方法;2)提供决定主轴前、后轴颈和内孔尺寸的刚度条件,可根据机床精度条件和刚度衰减系数曲线求解;3)建立了主轴组件受力变形模型和弹性力学条件;4)讨论了刚性支承与弹性轴和弹性支承与刚性轴两种情况下主轴端的挠度和柔度,用数值分析法得到柔度与跨距的关系曲线;5)运用数值分析法获得主轴最佳跨距线图,并用示例说明其迭代算法。可方便地确定主轴轴颈尺寸、内孔直径及主轴最佳支承跨距。
[1]杜君文.机械制造技术装备及设计[M].天津:天津大学出版社,1998.
[2]徐鹏.简明材料力学[M].北京:电子工业出版社,2011.
[3]刘卫国.MATLAB程序设计与应用[M].北京:高等教育出版社,2006.
[4]宋叶志.贾东永.MATLAB数值分析与应用[M].北京:机械工业出版社,2009.
