基于Lobatto-Gauss结构的五次元有限体积法

张栏辉，李永海

(1.吉林大学数学研究所，长春 130012;2.吉林大学数学学院，长春 130012)

基于Lobatto-Gauss结构的五次元有限体积法

张栏辉1，李永海2

(1.吉林大学数学研究所，长春 130012;2.吉林大学数学学院，长春 130012)

构造基于Lobatto-Gauss结构的有限体积法，试探空间取六次Lobatto多项式零点为插值节点的Lagrange型五次有限元空间，检验函数空间取五阶Gauss多项式零点为插值节点的分片常数空间.证明了这种格式的稳定性和收敛性以及在应力佳点导数的超收敛性，并通过数值实验验证了理论分析结果.结果表明，所给方法具有最优的H1模和L2模误差估计.

两点边值问题;五次有限体积法;超收敛;误差估计

在［-h，h］上的零点为

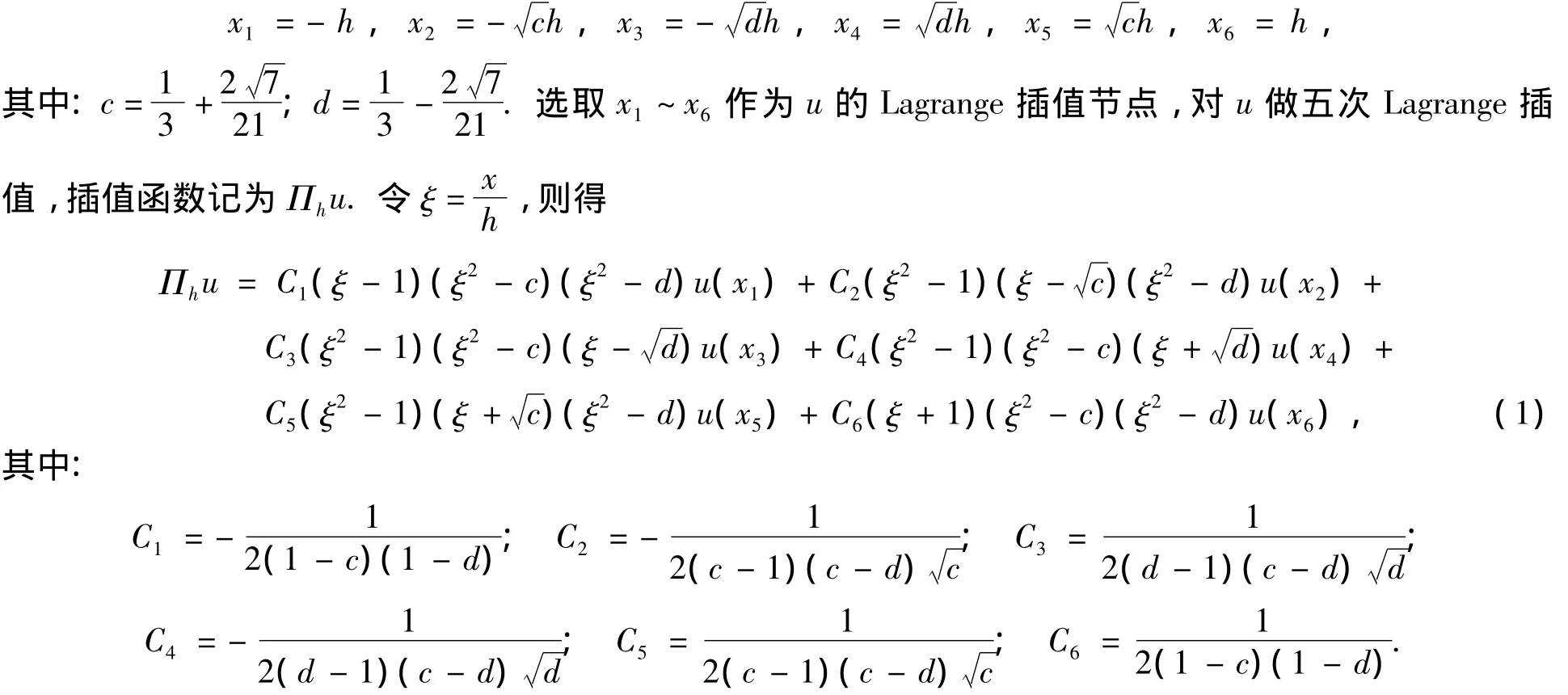
将u(xi)(i=1～6)在区间［-h，h］上任意一点x0处做Taylor展开，则得

本文将试探空间取为以六次Lobatto多项式零点为差值节点的Lagrange型五次有限元空间，检验函数空间取为以五阶Gauss多项式零点为插值节点的分片常数空间，定义五次元有限体积法格式，并证明了格式的稳定性，给出了五次有限体积元法在H1模和L2模下的最佳收敛阶估计及最大误差和误差导数的超收敛性分析，并结合数值算例验证了理论结果的正确性.

1 有限体积元格式

考虑两点边值问题:

其中:I=［a，b］;p∈C1(I)，p(x)≥pmin＞0;q∈C1(I)，q≥0;f∈H0(I).

1.1 初始剖分及试探空间

对区间［a，b］做剖分Th，剖分节点记为a=x0＜x5＜… ＜x5n-5＜x5n=b，剖分单元记为Ii=［x5(i-1)，x5i］(i=1，2，…，n).其中步长hi=x5i-x5(i-1).对于i=1，2，…，n，记

假设h=max{hi}，且剖分满足正则性条件hi≥ μh(i=1，2，…，n)，其中μ为一个正常数.取试探函数空间Uh为相应于剖分Th的Lagrange型五次元有限空间，即Uh中的函数uh满足下列条件:

1)uh∈C(I)，u(a)=0;

2)uh在每个单元Ii=［x5(i-1)，x5i］上是五次多项式，它由单元端点及单元内点x5i-5，x5i-4，x5i-3，x5i-2，x5i-1，x5i(i=1，2，…，n)的值确定.

Uh是U=H1E(I)的一个5n维度子空间，其中

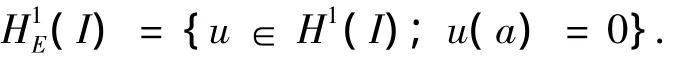
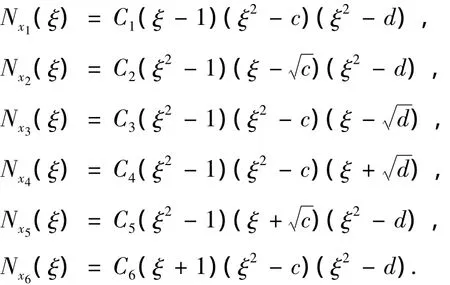
令φ5i-5=Nx1(ξ)，φ5i-4=Nx2(ξ)，φ5i-3=Nx3(ξ)，φ5i-2=Nx4(ξ)，φ5i-1=Nx5(ξ)，φ5i=Nx6(ξ).设ui=uh(xi)，利用插值基函数构造Uh的基底，对任意的uh∈Uh在单元Ii=［x5i-5，x5i］上可表示为

1.2 对偶剖分及检验空间

做相应于初始剖分Th的对偶剖分，在剖分单元Ii上，令x5i-5+k1=x5i-5+k1h，x5i-5+k2=x5i-5+k2h，x5i-5+k3=x5i-5+k3h，x5i-5+k4=x5i-5+k4h，x5i-5+k5=x5i-5+k5h，则对偶单元的节点为

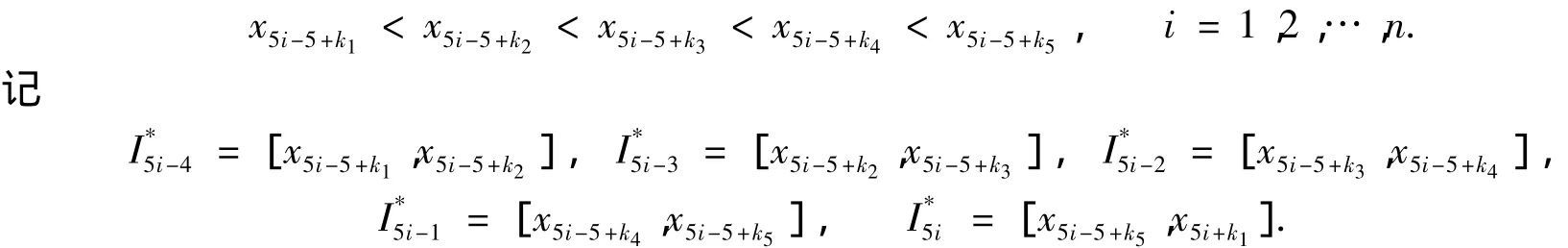
检验函数空间Vh取相应于的分片常数空间，它由下列基函数张成的5n维子空间构成:

则对任意一个函数vh∈Vh，有

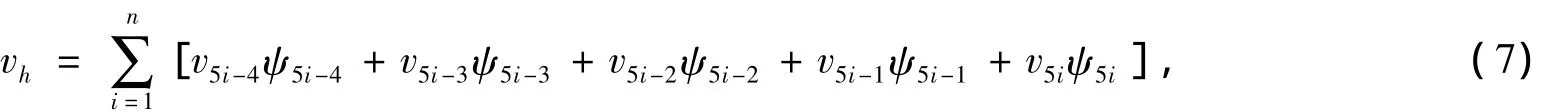
其中:v5i-4=vh(x5i-4);v5i-3=vh(x5i-3);v5i-2=vh(x5i-2);v5i-1=vh(x5i-1);v5i=vh(x5i).

1.3 有限体积元格式

求解方程(4)的五次有限体积元格式为:求uh∈Uh，使得

即对于i=1，2，…，n，规定u0=0，p5n+k1=0，x5n+k1=0.将积分做近似可得:

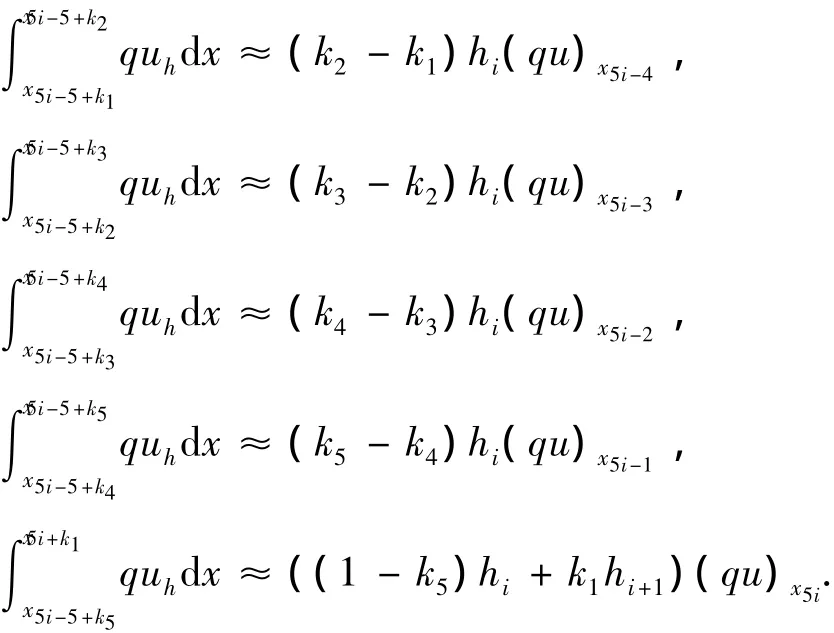
从而可得差分方程:

2 误差估计

为了做误差估计，先引入如下离散范数:

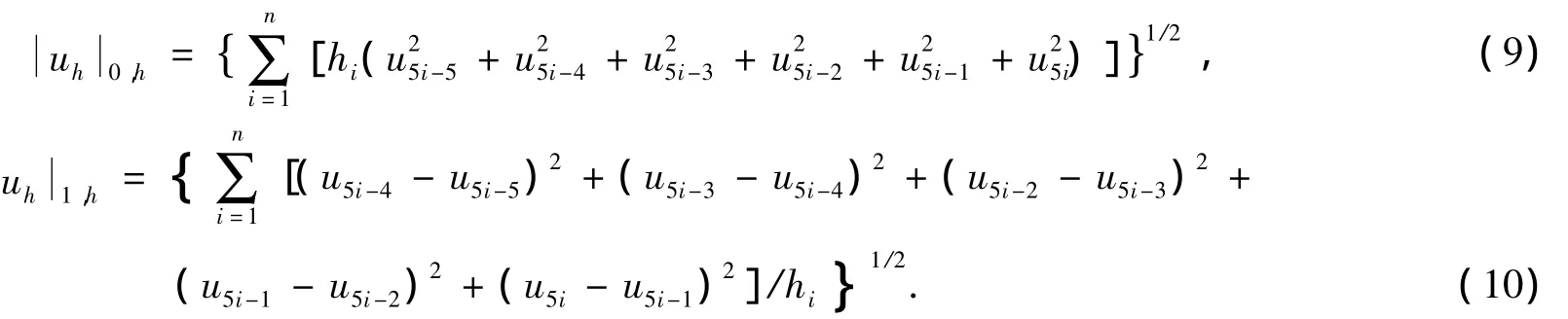
引理1 在Uh中价，即存在与Uh无关的常数α1，α2，α3，α4＞0，使得下式成立:

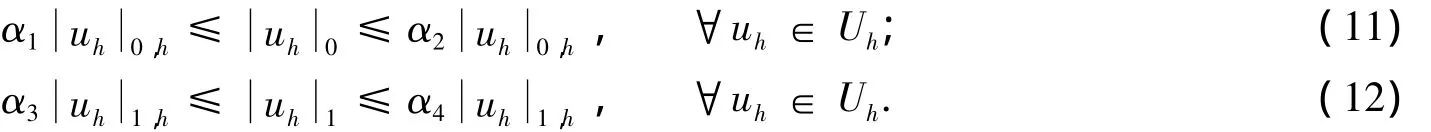
证明:由式(6)可得

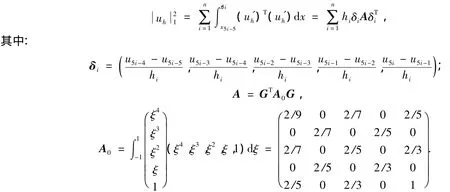
可以验证矩阵A0为对称正定矩阵，且G为非奇异矩阵，所以存在与Uh无关的正常数c1，c2，使得

即式(12)成立，同理可证式(11)成立.证毕.

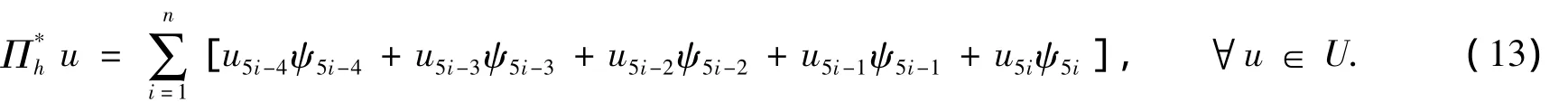
根据Soblev空间插值理论可得:

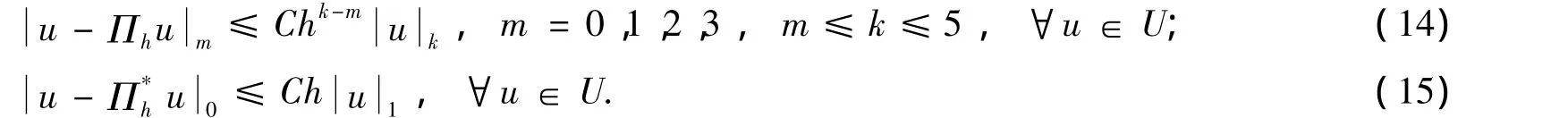
其中C为与u无关的常数.

定理1 当h充分小时，双线性形式a(uh，uh)正定，即存在与子空间Uh无关的常数β＞0，使得

证明:对于双线性形式，有

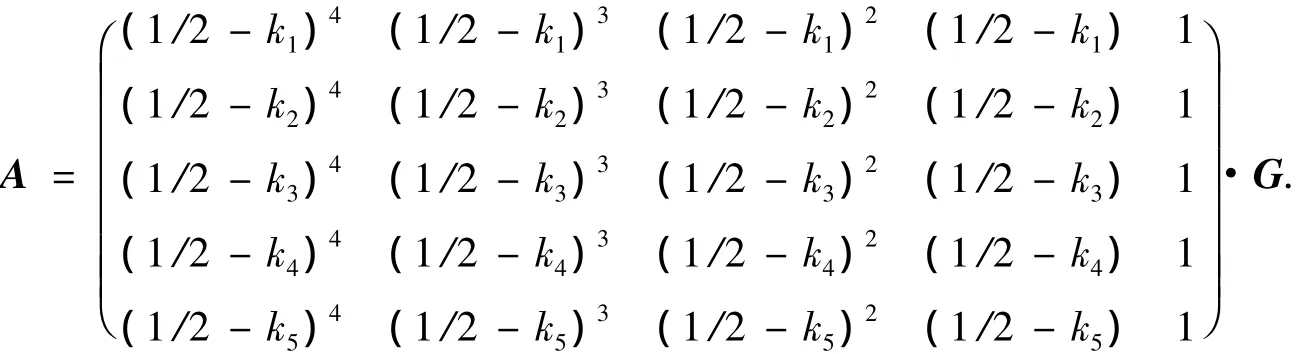
先估计 ~a(uhuh)，将矩阵Bi对称化为Ci=(Bi+)/2，则有

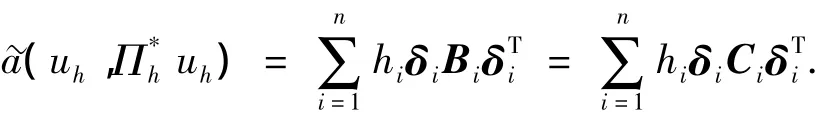
易验证矩阵Ci的顺序主子式大于零，所以Ci为对称正定矩阵，从而存在β1＞0，使得

再注意到q∈C1(I)及

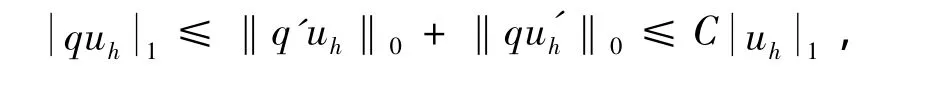
从而有

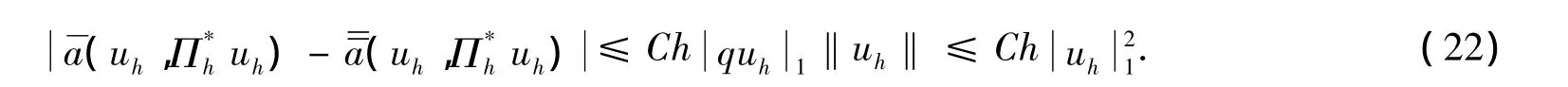
由式(20)～(22)可知，当h充分小时，存在β＞0，使得

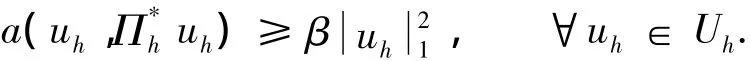
证毕.

注1 文献［10］的正定性分析方法只适用于采取Gauss点作为对偶剖分节点的情形，而本文采取了单元正定性分析方法，适合任何节点作为剖分节点的情形，例如剖分节点为等分节点或者Guass节点.

定理2 若问题(4)的解u∈(I)∩H6(I)是五次元差分格式(9)的解，则有误差估计:

证明:由于

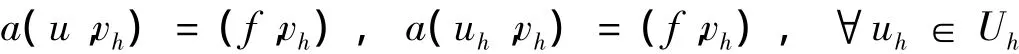
成立，所以

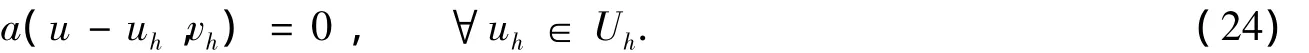
设Πhu为u向Uh的插值投影，则由定理1可得

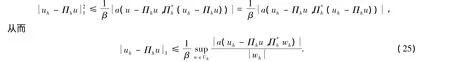
利用Cauchy不等式得

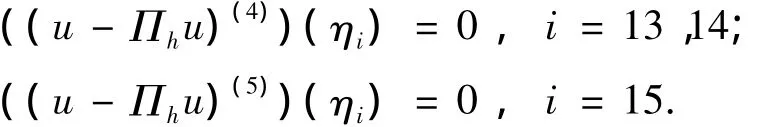
于是可得

当u∈(I)∩H6(I)时，有

另一方面，由

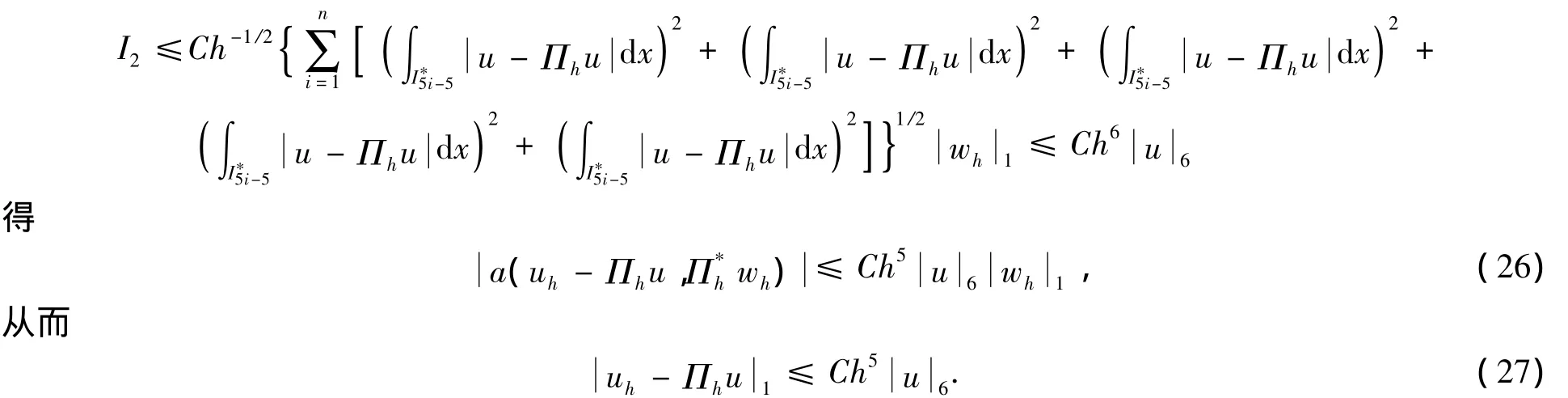
当u∈(I)∩H6(I)时，由逼近理论的结果知，，所以

证毕.

3 超收敛性分析和L2模误差估计

定义1 如果存在q∈［1，∞］，使得

则称点x0为应力佳点.其中:Πh是插值算子;E表示含有x0单元的并集;)表示在各个含有x0单元上▽v(x0)值的算数平均;N为区域的维数;C是与剖分Th和函数u无关的常数.与有限元法的情形类似，可得与有限元法类似的应力佳点定理.

引理2［1］设u，uh分别为边值问题(4)及五次有限体积格式(9)的解，相应的双线性形式满足如下差值弱估计:存在p∈［1，∞］，使得

则有‖u-Πhu‖1≤Chk+1‖u‖k+2，p，E.令Nk为插值应力佳点集，对于x0∈Nk，则有

其中r为Nk点数.

定理3 设u，uh分别为边值问题(4)及五次有限体积格式(9)的解，则有如下相应的插值弱估计:

证明:由已知条件可得

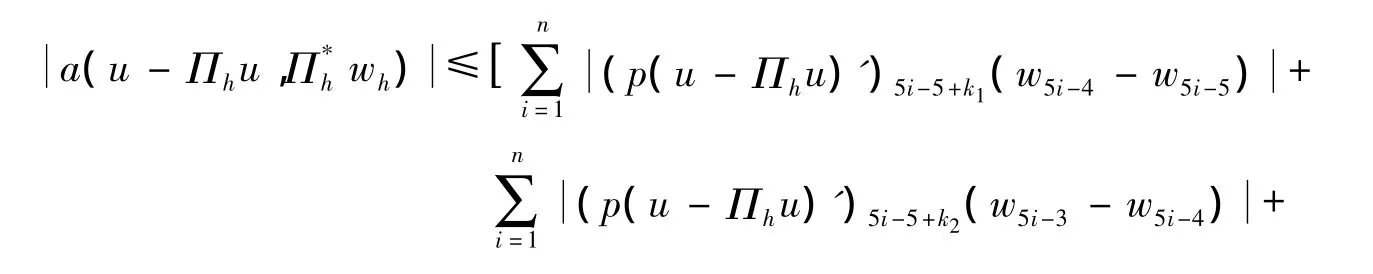
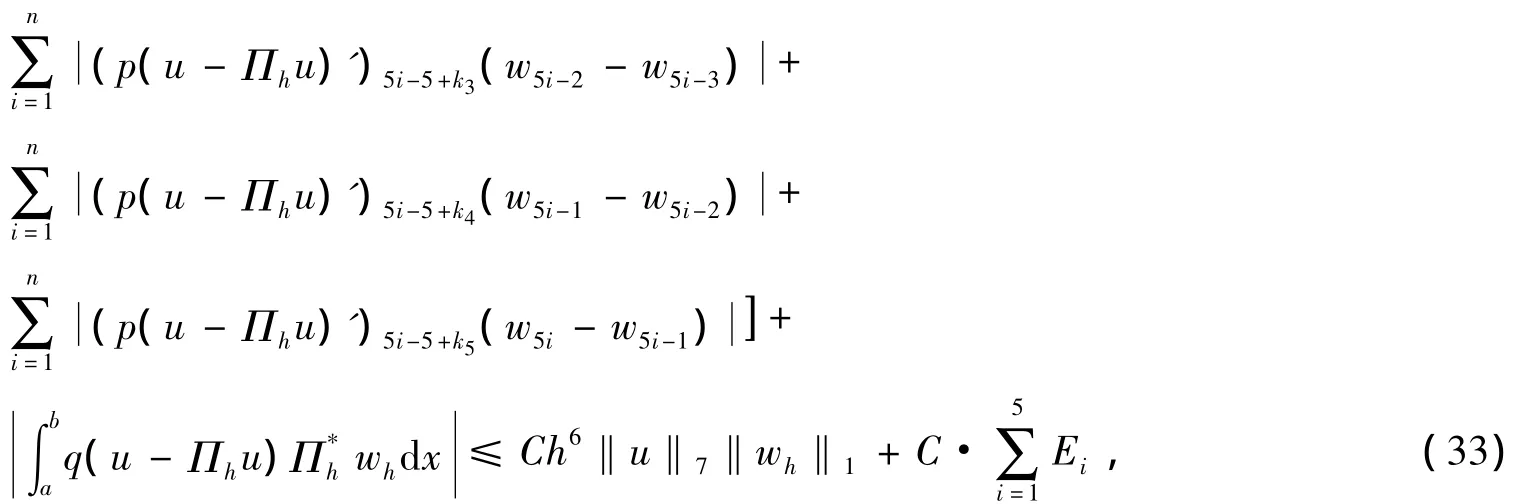
由Cauchy不等式得

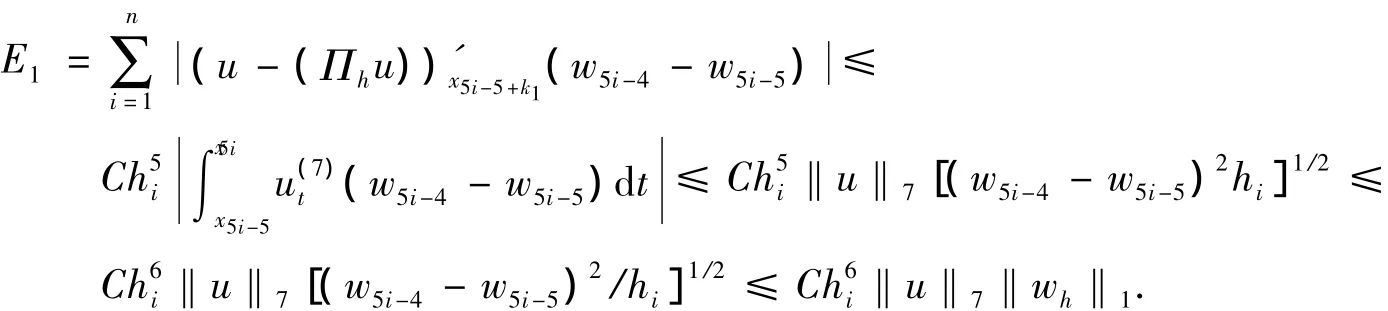
同理可证明Ei≤Ch6‖u‖7‖wh‖1，i=2，3，4，5.由式(33)可得所证结论.证毕.

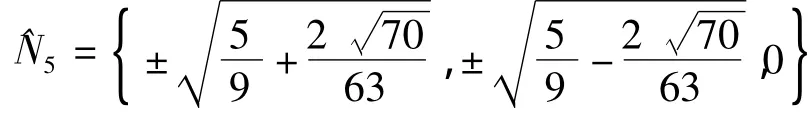
结合引理2和定理3可得:

定理4 设问题(4)的解u∈(I)∩H7(I)，uh是五次元差分格式(9)的解，则有:

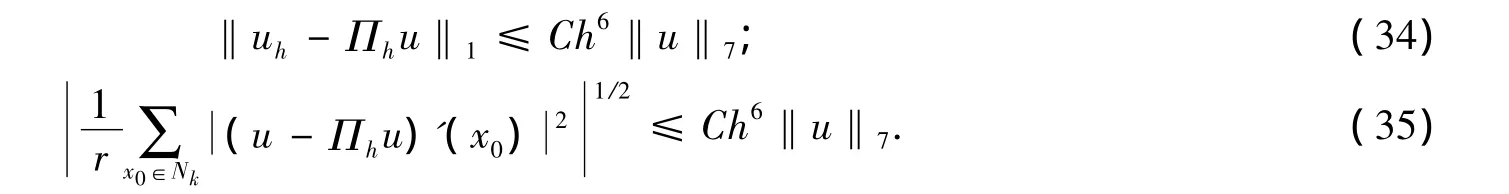
定理5 设问题(4)的解为u∈(I)∩H7(I)，uh是五次元差分格式(9)的解，则有

4 数值算例

下面通过数值算例验证误差的收敛阶.为方便叙述，本文所构造的一维五次Lobatto-Guass结构有限体积法记为方法1;采取等距节点上的五次Lagrange函数作为试探函数，并应用插值函数的导数超收敛点作为对偶剖分节点的有限体积法记为方法2.用max表示剖分节点处的误差最大模;Esup表示对偶剖分节点上平均导数的收敛性估计.

例1

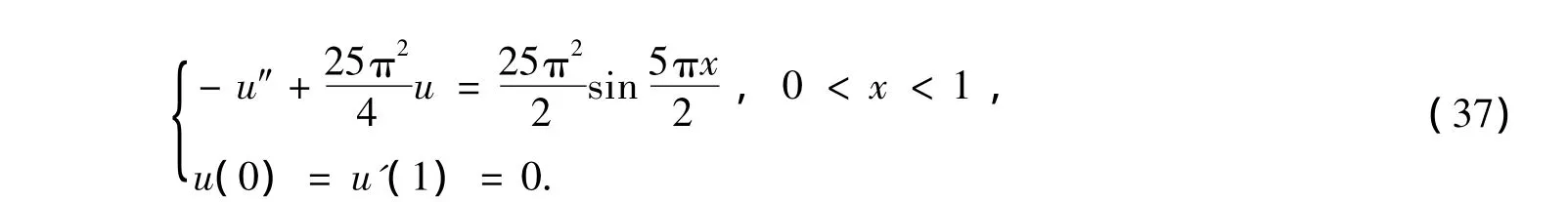
表1 方法1计算例1的数值结果Table 1 Numerical results of the first method about example 1

表2 方法2计算例1的数值结果Table 2 Numerical results of the second method about example 1

由表1和表2可见，方法1和方法2具有相同的H1和L2模，但在节点处方法1函数的超收敛性比方法2大一阶，且方法1比方法2相对误差较小，与理论分析结果一致.

［1］ LI Ronghua，CHEN Zhongying，WU Wei.Generalized Difference Methods for Differential Equation-Numerial Analisys of Finite Volume Methods［M］.New York:Marcel Dekker，2000.

［2］ 李荣华.两点边值问题的广义差分法［J］.吉林大学自然科学学报，1982(1):26-40.(LI Ronghua.Generalized Difference Methods for Two Point Boundary Value Problems［J］.Acta Scientiarum Naturalium Universitatis Jilinensis，1982(1):26-40.)

［3］ 于长华，李永海.解两点边值问题的基于应力佳点的二次有限体积元法［J］.吉林大学学报:理学版，2009，47(4):639-648.(YU Changhua，LI Yonghai.Quadratic Finite Volume Element Method Based on Optimal Stress Points for Solving Two-Point Boundary Value Problems［J］.Journal of Jilin University:Science Edition，2009，47(4): 639-648.)

［4］ 郭伟利，王同科.两点边值问题基于应力佳点的一类二次有限体积元方法［J］.应用数学，2008，21(4): 748-756.(GUO Weili，WANG Tongke.A Kind of Quadratic Finite Volume Element Method Based on Optimal Stress Points for Two-Point Boundary Value Problems［J］.Mathematica Applicata，2008，21(4):748-756.)

［5］ Plexousakis M，Zouraris G E.On the Construction and Analysis of High Order Locally Conservative Finite Volume-Type Methods for One-Dimensional Elleptic Problems［J］.SIAM J Numer Anal，2004，42(3):1226-1260.

［6］ GAO Guanghua，WANG Tongke.Cubic Superconvergence Finite Volume Element Method for One-Dimensional Elliptic and Parabolic Equations［J］.Journal of Computational and Applied Mathematics，2010，233(9):2285-2301.

［7］ 于长华，王晓玲，李永海.解两点边值问题的一类修改的三次有限体积元法［J］.计算数学，2010，32(4):385-398.(YU Changhua，WANG Xiaoling，LI Yonghai.A Class of Modified Cubic Finite Volume Element Method for Solving Two-Point Boundary Value Problems［J］.Mathematica Numerica Sinica，2010，32(4):385-398.)

［8］ 李莎莎，左平.一维Lagrange四次元有限体积法的超收敛性［J］.吉林大学学报:理学版，2010，50(3): 397-403.(LI Shasha，ZUO Ping.Superconergence of One Dimension Lagrange Fourth-Order Finite Volume Element Method［J］.Journal of Jilin University:Science Edition，2010，50(3):397-403.)

［9］ 郑文化.一维四次Lobatto-Gauss结构有限体积法［D］.长春:吉林大学，2013.(ZHENG Wenhua.One Dimension Fourth-Order Finite Volume Method Based on the Lobatto-Gauss Constructure［D］.Changchun:Jilin University，2013.)

［10］ CAO Waixiang，ZHANG Zhinmin，ZOU Qingsong.Superconvergence of Any Order Finite Volume Schemes for 1D General Elliptic Equations［J］.Journal of Scientific Computing，2013，56(3):566-590.

(责任编辑:赵立芹)

Fifth-Order Finite Volume Method Based on the Lobatto-Gauss Constructure

ZHANG Lanhui1，LI Yonghai2
(1.Institute of Mathematics，Jilin University，Changchun 130012，China; 2.College of Mathematics，Jilin University，Changchun 130012，China)

A one-dimension fifth-order finite volume method based on the Lobatto-Gauss constructure was designed，with its trial function being the fifth order Lagrange interpolated function，and the test function space being a piecewise constant space.The stability and convergence of the scheme was proved.The H1and L2error estimates were proved to be optimal.We discussed the superconvergence of numerical derivatives at optimal stress points.And the numerical experiments show the results of theoretical analysis.

two-point boundary value problem;fifth-order finite volume element method;superconvergence; error estimate

O241.3

A

1671-5489(2014)03-0397-11

10.13413/j.cnki.jdxblxb.2014.03.01

0 引 言

有限体积元法(FVEM)［1］由于具有结构简单和保持局部物理量守恒性等优点而广泛应用于各种数学物理问题中，目前已取得了许多研究成果.文献［2］给出了两点边值问题的有限体积法;文献［3-4］给出了二次有限体积元格式的H1模和L2模误差估计;文献［5］构造了一种新的一维高次元有限体积法，它使用应力佳点作为对偶单元的节点，保证了有限体积法与相应有限元法双线性形式的差是小量，从而借助于有限元法获得了有限体积法的各种收敛阶估计;文献［6-9］分别给出了三次和四次有限体积元格式的H1模和L2模误差估计，并采用基于应力佳点的有限体积元法，在理论和数值上给出了超收敛性的证明.本文在文献［9］的基础上构造一种更高次的有限元格式，先在区间［-h，h］上取六次Lobatto多项式的零点.六次Lobatto多项式

2013-09-23.

张栏辉(1991—)，男，汉族，硕士研究生，从事偏微分方程有限体积法的研究，E-mail:1050099567@qq.com.

国家自然科学基金(批准号:11076014).