流体黏度的实验研究
2014-09-12俞天伦马世红
俞天伦,马世红
(复旦大学 物理学系,上海 200433)
1 引 言
液体的黏性系数简称黏度,是描述液体内摩擦性质的重要的物理量,能够表征液体反抗形变的能力,而只有在液体内存在相对运动时才会表现. 在高等学校开设的大学物理实验课程中,测量黏度的常用方法有落球法[1]及毛细管法. 2种方法各有利弊:落球法对于小球的形状、质量以及放入量筒的位置要求较高,限于较高黏度的液体,例如蓖麻油;毛细管法对于已知黏度的液体要求较高(温度、杂质等),限于较低黏度的流体且易于被清洗,例如水和酒精,且对仪器的维护困难. 本文基于泊肃叶公式,制作了简单的测量装置,可以实现低成本、测量范围可调、可控精度比较高的黏度测量.
2 实验原理及其装置
2.1 黏度与雷诺数
黏滞力是流体受到剪应力变形或拉伸应力时所产生的阻力,是黏性液体内部的流动阻力. 黏滞力主要来自分子间相互的吸引力.
剪切黏度:2个板块之间流体的层流剪切. 流体和移动边界之间的摩擦导致了流体剪切,描述该行为强度的是流体的黏度. 在一般的平行流动中,剪切应力τ正比于速度u梯度(图1),即
式中η即黏度[2].
(1)式假设流动是沿着平行线的层流状态,并且垂直于流动方向的y轴指向最大剪切速度. 满足剪切应力-速度梯度线性关系方程的流体被称作“牛顿流体”.
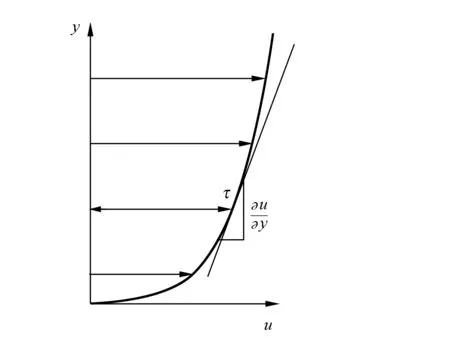
图1 剪切黏度的示意图
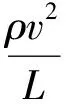
2.2 泊肃叶公式及其应用
泊肃叶公式[3-4]:牛顿流体在圆管内处于层流状态,L为管长,p为圆管两端压强差,a为圆管半径(如图2所示),则在管内的流量:
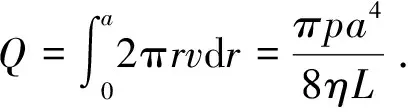
容器是圆柱体处于大气压下(如图2所示),且水位下降足够慢(准静态过程),使圆管中水流保持层流状态,可以认为p=ρgy,此时射出的水流应呈抛物线状且平稳,则有:
其中A=πR2是容器的截面积. 求解(3)式可以得到:
对(4)式两边同时乘以容器的截面积A,得:
式中V为容器中的液体有效体积,即图2中y所对应的体积,V0为初始有效体积.
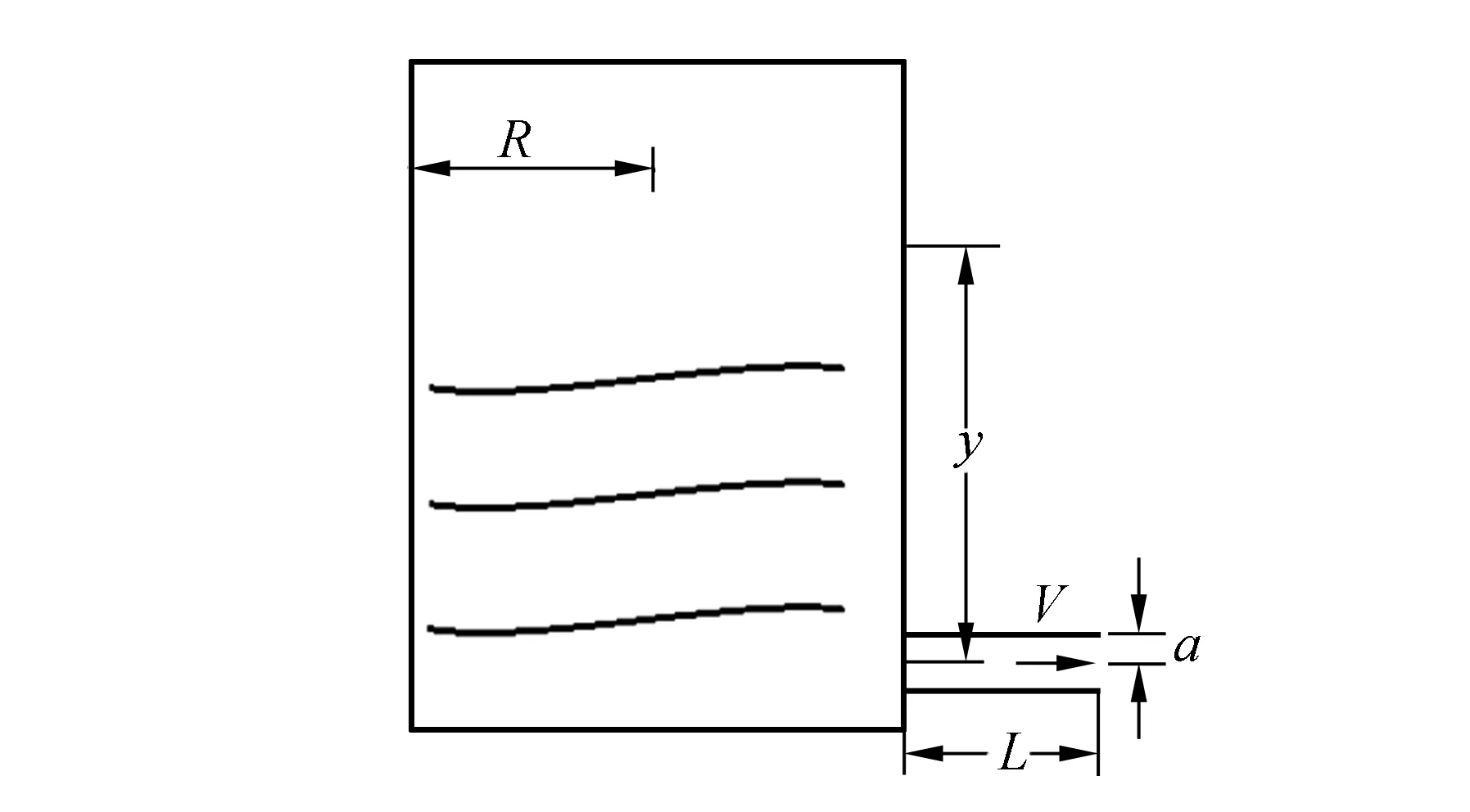
图2 实验装置示意图
2.3 装置
实验装置如图3所示,其主体是2 L的量筒(圆柱形容器),在其侧壁上,以200 mL处为中心,开出直径约3.8 mm的圆孔,之后接上长度适中的橡胶软管(内径3.72mm)并用502胶水固定. 圆管采用的是多种内径四氟乙烯管(内径分别为1.2 mm,1.6 mm,2.0 mm,2.8 mm),剪裁合适的长度后,利用502胶水固定在连接件内,之后连接于软管中. 采用这种方案便于更换不同内径的流管以测量不同黏度范围的液体.

图3 实验装置实物图
其余测量工具有:秒表、直尺、温度计等. 实验中的待测液体为水和羧甲基纤维素纳(简称CMC)溶液.
3 实验结果与讨论
选择一定规格的圆管组合连接于软管中(如图4所示结构),将待测液体注入量筒中,直到超过2 L刻度线200~300 mL. 确认装置各连接处没有漏水后,将软管按住稍向下倾斜,使液体流出圆管并排除气泡. 可以观察到此时流出的水流呈抛物线状,并且较为平稳,射程随时间缓慢减小. 再次确认装置各连接处没有漏水,调整圆管使其保持水平.
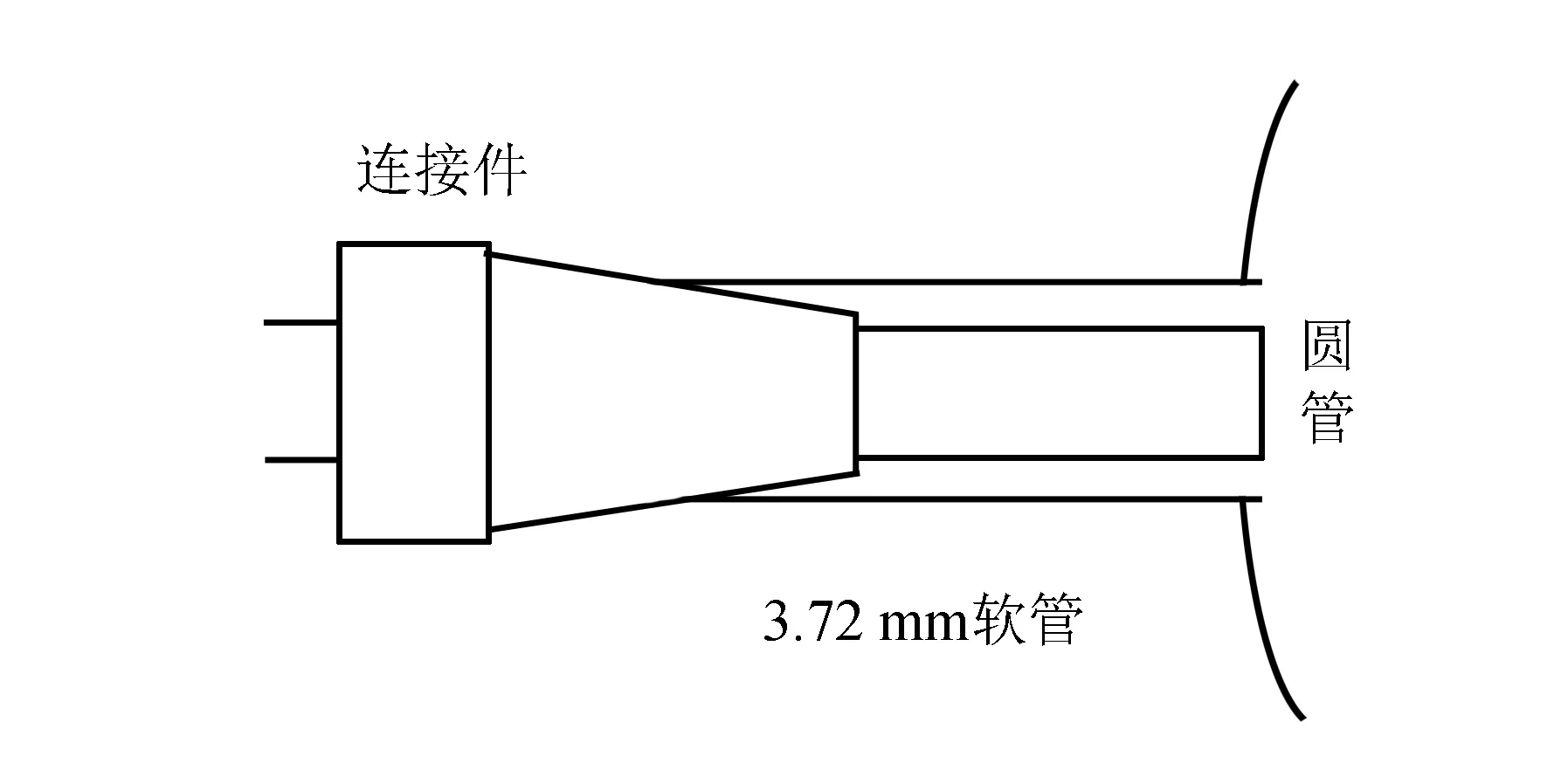
图4 俯视结构示意图
当确认圆管中气泡排除后,则可选择合适的液面位置开始计时. 根据液面下降的速度,选择合适的体积间隔(一般选为最小刻度的1~2倍,即20 mL或者40 mL)并计时. 在至少采样10个点之后,利用V=aebt进行拟合并求出η. 随后通过求导以及截面的换算,推出速度v的范围,则进一步可得到Re的范围.
使用内径2a=(1.20±0.01) mm,长度L=(14.90±0.01) cm的四氟乙烯管,水温19.7 ℃时,拟合结果如图5所示.
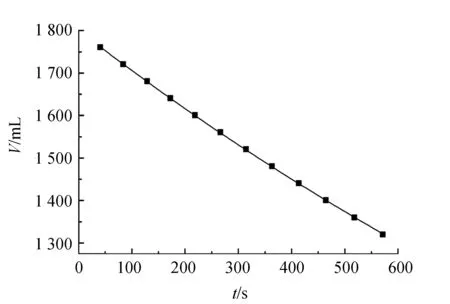
图5 19.7 ℃下水的拟合结果
算出η=1.032 mPa·s,不确定度分别由重力加速度g、流管半径a、流管长度L、量筒半径R以及拟合参量b的不确定度贡献:
得到u(η)=0.018 mPa·s.
参考值可以查表[5]得到温度为整数时的黏度. 对于温度不是整数的情况,采用加权平均的方式得到参考值. 例如:实际水温为19.7 ℃,水在19 ℃和20 ℃时理论黏度为1.029 9 mPa·s和1.005 0 mPa·s,计算参考值时前者权重为0.3,后者权重为0.7,得到参考值η参考=1.012 5 mPa·s. 测量值相比参考值,相对偏差Δ=1.9%.
进一步处理后,得到圆管中速度v的范围在0.59~0.85 m/s,从而分别得到由η测量计算的Re范围在690~985,由η参考计算的Re范围在700~995.
对19.7 ℃做3次测量,得到的黏度相差不超过6%,具有可重复性. 通过3次的结果得到平均值η=(1.06±0.04) mPa·s,相对偏差Δ=4.7%.
对水所有实际采样过程中,通过拟合的V=aebt处理,得到水面下降速度在10-4m/s量级;圆管中水流速度在10-1m/s量级,Re均在1 000以下,属于层流,排除了流体处于紊流或者湍流状态. 如果处于紊流(湍流)状态,测得的黏度将是与流速、环境因素等相关的表征值而非物质的本征性质.
表1中所测得的黏度η测量相比理论值η参考有一定的偏差,产生偏差的原因可能是:
1)所用的四氟乙烯管并非理想的直线型,有小量的弯曲,使水流在经过弯曲处时动能减损,导致测量结果偏大;
2)水流在从量筒进入圆管的一小段位置,其实是突变界面的流动,这一小段的水流受到的局部阻力较大,导致测量结果偏大;
3)水中含有杂质,影响不可知;
4)量筒、圆管的材料,热膨胀系数在10-6~10-5℃-1量级,在测量的温度范围可以忽略不计.
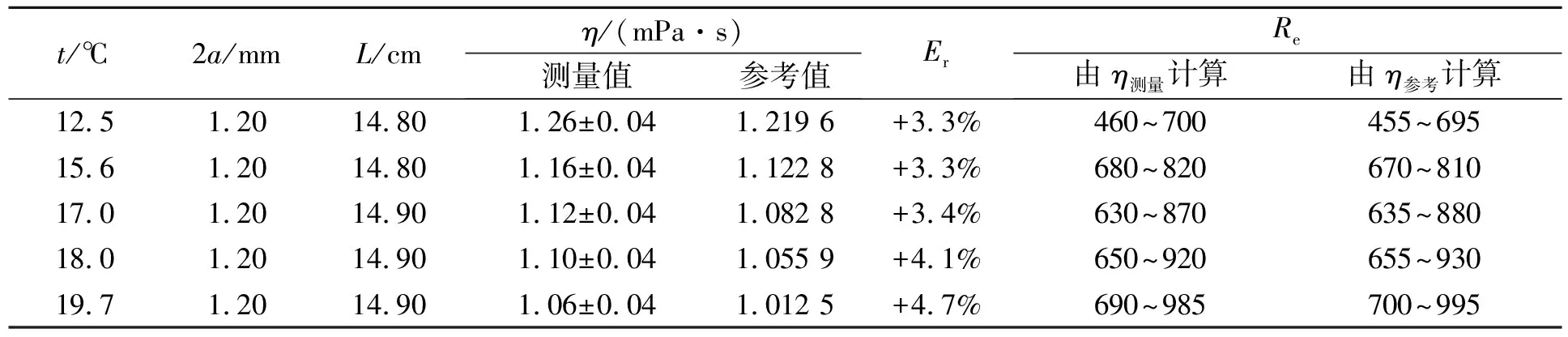
表1 不同温度下水的黏度测量结果
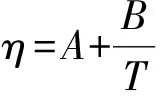
使用这套简易测量装置,在这5个温度下均分别做过多次测量,误差最大不超过7%,最接近参考值的测量值误差均不超过2%,平均误差不超过5%.
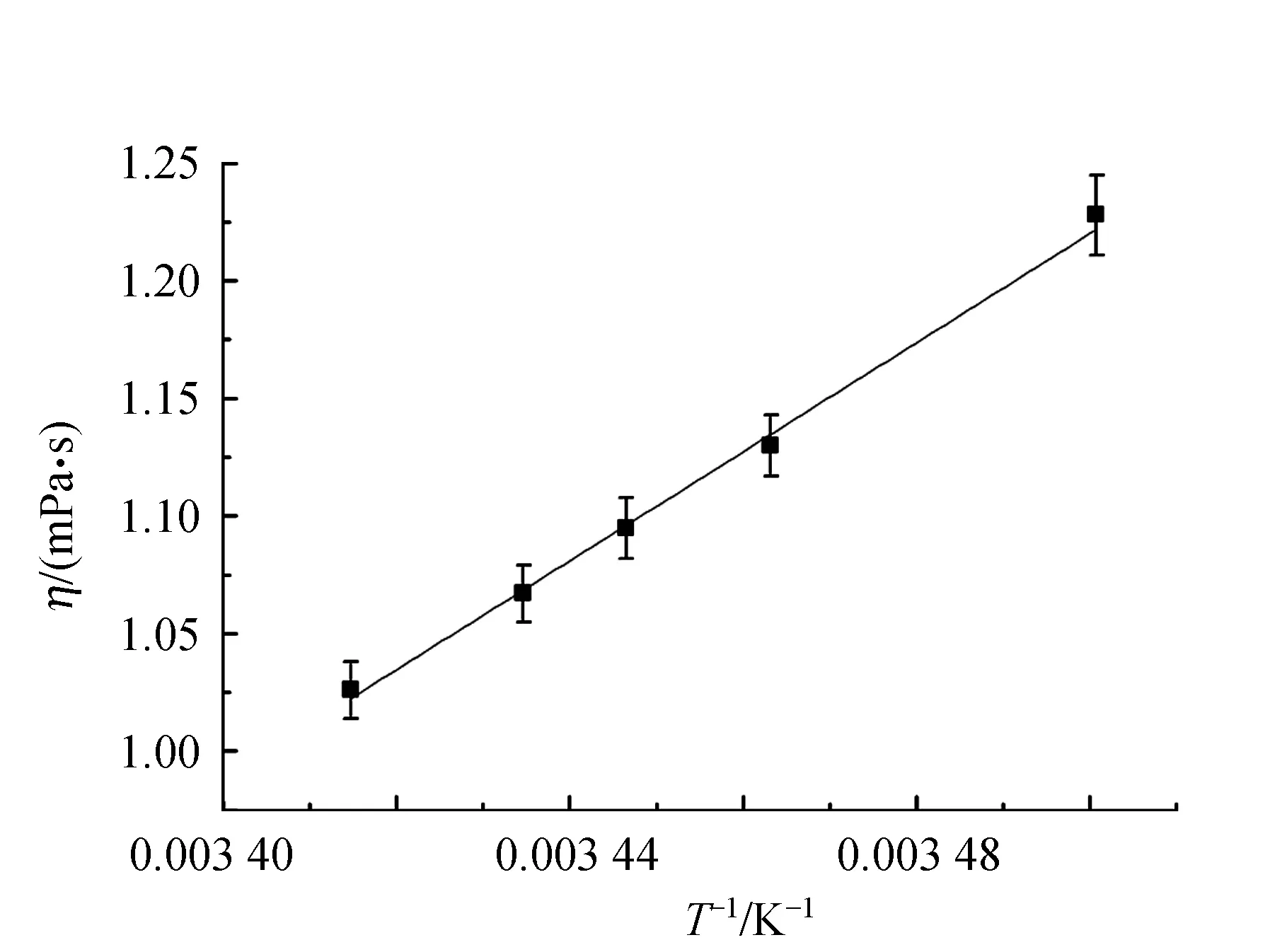
图6 水的黏度与温度的关系
羧甲基纤维素钠(CMC)是一种常用的高分子聚合物增稠剂. 在测量的质量分数范围内,均属于牛顿流体[未出现无管虹吸[7]现象且符合由牛顿流体推出的(5)式]. 在配置溶液时,发现:1)其密度比水大(例如在2 500 mL水中加入约20 g CMC,当充分溶胀后,溶液体积会减少约50 mL);2)完全溶胀后,分布不均匀,在容器底部溶质稍多于液面处(在移液时可以观察到底部的黏度稍大). 所以计算密度时,引入3%的不确定度,且质量分数一列指的是测量时的CMC溶液质量分数不超过该值(但偏差不大).
CMC溶液的黏度测量结果如表2所示.
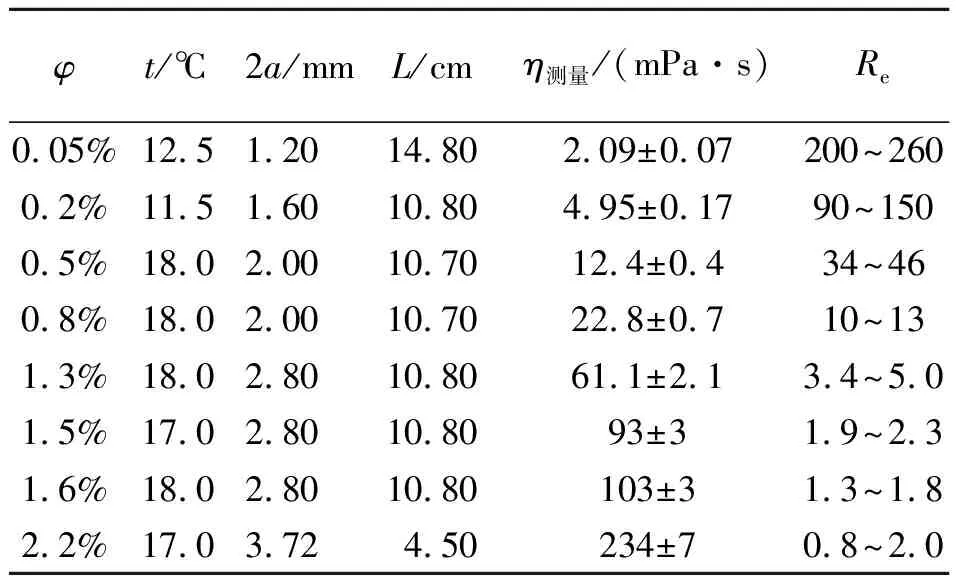
表2 CMC溶液的黏度测量结果
测量出的黏度与文献[8]中测出的黏度均在同一量级上,且在相应质量分数点均偏小. 由于制作过程、杂质含量等不同,其CMC相同质量分数的溶液黏度会有变化. 基于这两点以及水的结果误差大小,可判断测得CMC溶液的黏度是可信的.
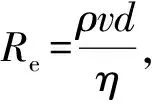
在测量范围内,排除温度差异相对较大的0.05%及0.2%这2个点后,发现其余的CMC溶液的黏度与质量分数有指数增长的规律(图7). 根据文献[9],部分多种组分的液体的黏度可以由Lobe法经验公式给出:
其中,η为黏度,ρ为密度,γ为体积分数,α为特性黏度参量,R为气体摩尔常量,T为绝对温度.
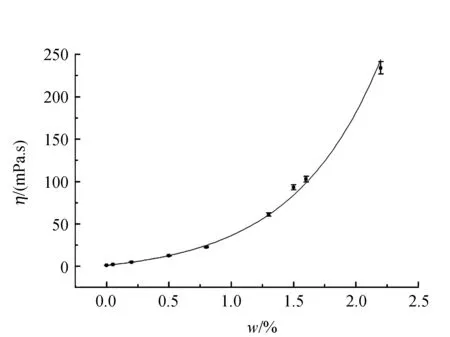
图7 CMC溶液的黏度与质量分数的关系
测量到的CMC溶液的黏度,在小范围内的质量分数变化下,满足简单的近似经验公式η=A+BeCφ(其中φ为CMC的质量分数),相关系数r2~0.997. 其物理机制与CMC分子对水分子的吸附、CMC分子的团簇作用与扩散运动等因素相关,目前没有完善的理论能包含不同种类的溶液.
4 结束语
使用自制的简易装置,测量了不同温度下水的黏度,与理论值相比误差较小. 在测量温度范围内,水的黏度与绝对温度的倒数呈线性关系. 用该装置测量了保持牛顿流体性质范围内的不同质量分数的CMC溶液,其黏度与质量分数呈指数增长. 该装置通过更换不同规格的圆管,在满足被测液体是层流状态且流速较低的条件下,使测量时间范围不过长(一般在5~15 min),实现了10-3~100Pa·s量级的黏度测量.
参考文献:
[1] 赵敏,强晓明. 落球法测液体黏度的改进[J]. 物理实验,2011,31(11):25-26.
[2] 欧特尔 H. 普朗特流体力学基础[M]. 北京:清华大学出版社,1982:237-239.
[3] 波蒂斯A M,杨H D. 大学物理实验——伯克利物理实验[M]. 北京:科学出版社,1982:187-191.
[4] 钱钧,惠王伟,张春玲,等. 毛细管法测量液体黏度实验再设计[J]. 物理实验,2012,32(6):1-4.
[5] 刘光启,马连湘,刘杰. 化学化工物性数据手册[M]. 北京:化学工业出版社,2002:1-12.
[6] 娄彦敏,刘娟红,周晓平,等. 温度对水的粘度和扩散系数影响的研究[J]. 西南师范大学学报(自然科学版),2009,34(6):34-39.
[7] 马宗豪. 定常流场下非牛顿流体在波壁管内的减阻特性[D]. 大连:大连理工大学,2009:1-2.
[8] 孙兰芬. 甲基纤维素、羧甲基纤维素钠、羟乙基纤维素溶液粘度的测定[J]. 河南大学学报(自然科学版),1987(4):64.
[9] 童景山,李敬. 流体热物理性质的计算[M]. 北京:清华大学出版社,1982:237-239.
[10] 沈元华,陆申龙. 基础物理实验[M]. 北京:高等教育出版社,2003:119-122.
[11] 贾玉润,王公治,凌佩玲. 大学物理实验[M]. 上海:复旦大学出版社,1987:141-142.
