塔斯基的真定义、语义学与逻辑后承

○朱建平

(苏州大学政治与公共管理学院，江苏苏州 215123)

塔斯基的真定义、语义学与逻辑后承

○朱建平

(苏州大学政治与公共管理学院，江苏苏州 215123)

塔斯基关于真的语义学定义和逻辑后承的里程碑式的著作是对现代语义学研究最重要的贡献。塔斯基用满足和归纳的方式给出的真的递归定义，循序渐进的句法定义，语义模型的概念，逻辑真和逻辑后承的概念等一系列理论和方法构成了当代语义学理论的核心部分。诸如模型论语义学、可能世界语义学、戴维森的意义理论、蒙太格的内涵语义学，甚至作为生成语法的分支的逻辑形式(LF)等无一不体现或者渗透着塔斯基原理和思想。

塔斯基;真理定义;语义学;逻辑后承

塔斯基的第二个目标是研究逻辑方法论，用塔斯基的说法是元数学。元数学(又称元逻辑)研究的是在一逻辑框架(一阶和高阶数理逻辑)中理论(特别是数学理论)的形式性质以及逻辑框架本身的性质。真的概念在元逻辑研究中(例如，在哥德尔完全性和不完全性定理中)扮演着重要的角色。然而由于这一概念会产生悖论。因而，塔斯基的第二个目标是证明“真”概念可以在元逻辑中一致性地被使用。［Vaught，1974］

达到这样一个目标并不要求一个明确的真定义。的确，在论文中塔斯基考虑了对这一问题的各种其他处理，诸如把真概念作为初始符号，给出一种公理的刻画等。通过一个明确的可消除的定义方式把真概念引入理论中只是满足上述挑战的一种方式。但是，与公理化的处理相比，后者具有一个非常重要的优势，即通过给出这样一种定义，经由被定义表达式的可消除性，我们能够保证如果初始理论是一致性，那么最终的理论也应当是一致的。

塔斯基的真理论是一种逻辑语义学，本质上是建立在逻辑与非逻辑概念划分的基础之上的。上世纪50年代中期，随着逻辑的扩展，塔斯基语义学在逻辑、哲学和语言学中也迅速传播和扩展。新的扩展提出并要求塔斯基语义学回答关于逻辑语义学的某些重要概念及其与语言学语义学的联系，而在某种程度上塔斯基语义学也提供了回答这些问题的工具和手段。本文将讨论塔斯基的语义学及其它本身未回答的问题，讨论并分析塔斯基语义学在随后的扩展中所遇到的各种质疑、批评，以及塔斯基语义学中的各种哲学问题。

二 塔斯基对说谎者悖论的解决

塔斯基关心的是真概念的一致性，他的这一目标的主要动机使真定义的可消除性成为关键。因为该定义的特征就在于它能保证真概念的引入不会带来矛盾。的确，没有这样一种特征，对真谓词的引入就需要一个清楚一致的证明;有了它，一致性就可以通过我们引入概念的程序而自动地得到保证。在一致性方面，哲学家面对的主要挑战是说谎者悖论。塔斯基系统地将这一悖论阐述如下:

令c是“印刷在本页第7行的句子的缩写”，考虑语句:

c不是真的。

显然，

(1)c=“c不是真的”，

(2)“c不是真的”是真的当且仅当c不是真的。

使用经典逻辑定理，我们从(1)和(2)推演出矛盾。

(3)c是真的当且仅当c不是真的。

悖论的根源是什么?塔斯基使用的前提似乎是无可挑剔的:(1)是一个容易验证的经验陈述，(2)是一个无争议的等同模式:

(E)x是真的当且仅当p的替代实例，其中“P”表示一句子，“x”表示这句子的名称。(这一模式的一个例子是“雪是白的”是真的当且仅当雪是白的。)假定经典逻辑的定律并不是引起悖论的原因，人们自然把目光转向c。c的一个显著特征是它断定了一种涉及真本身的性质。塔斯基认为悖论的根源就在于此，一种包含它自己的真谓词以及它的句子名称的语言。塔斯基将这类语言称为语义封闭的。假定这种语言有一个合理的逻辑装置，它就会形成悖论语句。由此，塔斯基得出的结论是语义学上封闭的语言是不一致的，即它们生成了不能一致性地给出真值的句子。我们不可能为这种语言一致性地定义真概念。这个结论绝不是无足轻重的。自然语言在下述意义上是普遍的，即被任何语言的说话者所说的任何事情也能够被该说话者在他的自然语言中被表达。因此，自然语言是一种语义封闭的语言，为这种语言定义真(和其他的语义学概念)是不可能的。

然而，不是所有语言都是语义封闭的。大多数数学语言和科学语言不是语义封闭的。塔斯基将其称为语义开放的语言。塔斯基对说谎者悖论的解决是将真理的定义限于语义开放的语言。这一解决要求我们把语言看作是置于一个层级之中。为一给定的开语言L(“目标”语言，用塔斯基的话来说是“对象语言”)定义真概念，我们必须提升到一个更高的(开)语言ML，或者元-L的层次上。该语言有指称L的(特别是，L中的句子)所有表达式的资源。我们在ML中为L定义真理概念。并依此类推，在第三层级的开语言中为ML定义真理概念等等。这一对悖论的处理称为语言分层的解决。

塔斯基特别关注一种特定的语言，即在现代数理逻辑框架中的形式化的语言。这种语言包括(1)真值函项完全集的逻辑常项的集合，存在和全称量词以及等值词;(2)变项的无穷集; (3)非逻辑常项的集合(可能是空集):个体常项、函项常项和谓词。因为只有被解释的语句能才是真的或假的。塔斯基将注意力放在被解释的语句，即它的初始常项(逻辑的或非逻辑的)是完全解释的那种语言。这样的语言是科学和数学语言的形式化以及自然语言的开放片段的形式化。塔斯基将这种语言称之为“形式化的语言”。他的目的是为这种形式化的语言定义真理概念。

三 塔斯基形式化语言真理定义的方法

(一)一般原理

1．对象语言和元语言。如果被讨论的语言(对象语言)是L，那么真的定义应当在作为元语言的ML中给出。元语言应当包含对象语言的副本(以使得任何能在L中被说的事物也能够在M中被说)，元语言也能够谈论L的句子以及它们的句法。最后，塔斯基允许ML包含集合论的概念和被解释为“是L的真语句”的1-位谓词符号“T”，即作为一个被且仅被L的真句子所满足的谓词。元语言的主要目的是形式化被谈论的对象语言。同样塔斯基也要求元语言应当有一个为定义和证明真定义的目的人们需要假定的一个表达一切事物的公理集。真定义本身是按照元语言的其他表达式的真定义。所以定义是按照句法学集合论和在L中可表达的概念的方式给出的，而不是按照像“指称”或者“意味”那样的语义学概念给出的。

2．形式正确。为了以一种形式正确的方式定义真，必须遵循形式正确定义的通常程序。特别是要确保定义L的真概念不在L中出现。而且作为定义，这个形式的语句必须是可证的等值式。等值式的可证性必须使用不包含真的元逻辑语言。

3．实质充分。形式正确虽然能够保证一致性，但不能保证被定义的概念能用于真谓词的目的。用塔斯基的话来说，定义不仅仅是“形式正确的，”而且也必须是“实质充分的。”换句说法，引入的谓词必须应用于所有的且仅仅是我们最初语言中的真语句。为了给出对一语言是充分的真谓词的定义，塔斯基要求它满足下列标准(塔斯基称为“约定”)即(T)标准:在(ML)中的T定义是一个L的真的实质充分定义当且仅当，对每一个L的句子σ，它蕴涵一个形式为

T(s)当且仅当p 的ML语句，其中“s”表示σ的ML的名称，“p”表示与σ同样内容的ML语句(对ML中的σ的翻译)。

上述的大致思想是，给定了一L的句子σ，L的真的充分定义蕴涵σ有性质T当且仅当在这个世界的事物与σ所说的一致。例如，如果σ表示“雪是白的”，T的定义蕴涵σ有性质T当且仅当事物雪(实际上)有是白的性质。为了满足这一要求，对每一L的句子σ，ML要求包含有一个与σ内容相同的句子。我们约定“雪是白的”是L句子中的“雪是白的”的ML名称，“雪是白的”是与“雪是白的”内容相同的ML句子。T的定义蕴涵ML-语句:

T(雪是白的)当且仅当雪是白的。

在ML中为L构造真理的定义，我们必须考虑在现代逻辑的框架内被形式化的任何语言中有许多句子这一事实。一个象T(s)当且仅当(s=雪是白的且雪是白的，或者s=草是红的且草是红的，或者…)这样的真理定义是不可能的，因为这样的定义会无穷长。为了避免这一困难塔斯基使用了递归的方法。只要某些条件被满足，递归定义能够使我们用一有穷的方式定义涉及无穷对象的谓词。这样的定义是有穷长的，它们在有穷多的步骤内确定是否一给定对象归属于一给定的谓词。这里我们不详述递归定义的条件，而是仅仅给出它的基本思想，即如果每一在L中的句子是从L的有穷多的原子语句通过有穷多的逻辑算子唯一生成的，如果在L中的原子语句和逻辑算子是有穷可说明的，那么L的真能够被定义。这样的定义确定了L的每一句子的真值是建立在——(1)它的原子成分的真值和(2)它的逻辑结构基础上的。例如，如果仅有的逻辑常项是否定和析取，那么通过说明(1)L的原子语句的真值，(2)给定了被否定语句的真值，确定一否定式真值的规则，(3)给定了析取支的真值，确定析取式真值的规则——的基础之上的。

然而，如果L包含有量词，那么L的真理定义不可能以如此方式加以定义。涉及量词的语句不是通过原子语句而是通过原子公式，包括那些具有自由变元(不在任何量词的辖域内的变元)以及没有真值的公式(例如，“∀xF(x)”是从有一个自由变元x的原子公式Fx生成的，因而Fx是没有真值的)的原子公式的方式生成的。但是，经由一个可应用于公式的辅助性概念“满足”的帮助，L的真理概念就是可定义的。满足概念是一个直觉的概念:原子公式“x是偶数”被0、2、4，…所满足(在一自然数的论域内)。更一般地，“Rx1，…Rxn”被一对象的n-元组＜a1，…，an＞所满足，当且仅当a1，…，an(有序地)处于关系R(被“R”所指称的关系)中。L的真理定义分两步实施:(1)给出L的“满足”的递归定义，(2)建立在(1)基础上的(非递归的)L的真理定义。

(二)塔斯基的例子

塔斯基通过一个例子解释了他的方法。

对象语言:Lc

作为目标的语言是类演算语言。在这里我们称之为Lc，Lc是被解释的一阶语言，它的初始词汇由逻辑常项“～”(否定)、“∨”(析取)和“∀”(全称量词)、非逻辑常项“”(类包含的2-位谓词)和涉及Lc的论域Dc(Dc是一类的集合)的所有对象的变元，“x1”，“x2”，“x3”，…。

元语言:MLc

Lc的真定义是在元语言MLc中进行的。MLc以上述方式联系到Lc。特别是(1)Lc的句法在MLc中被描述;(2)每一个Lc的常项在MLc都有一个名称和翻译(具有相同意义的常项); (3)MLc有一个未加定义的，指示Lc中的真谓词的1-位谓词“T”，以及作为Lc的语义学谓词的另外一个可定义谓词;(4)MLc有一个与Lc的变元相比的高阶变元(或者比Lc更丰富的集合论装置)。

定义(在MLc中)

记号:令“vi”和“vj”表示Lc中的任一变元xi和xj的模式符号。令“Φ”、“Ψ”和“σ”表示Lc中任一表达式的模式符号。令“「”和“」”代表引号，其中“「Φ∨Ψ」”表示公式Φ，符号“∨”和公式Ψ按序毗连的结果。对每一Lc的初始常项c，令c是MLc语言中c的名字，且c是对MLc中的c的翻译。

(三)(Lc的)公式—归纳定义

1．「vivj」是公式

2．如果Φ是公式，那么「～Φ」是公式。

3．如果Φ和Ψ是公式，那么「Φ∨Ψ」是公式。

4．如果Φ是公式，「∀viΦ」是公式。

5．只有通过1-4获得的公式才是公式。

σ是句子当且仅当σ是没有变元自由出现的公式。令g是任意一个指派Lc的变元到在Lc域Dc中的一个对象，我们称g是L的指派函项，且指称g(vi)为“gi”。

(四)(Lc的公式的)满足-递归定义

1．g满足「vivj」当且仅当gigj。

2．g满足「～Φ」当且仅当～(g满足Φ)。

3．g满足「Φ∨Ψ」当且仅当g满足Φ∨g满足Ψ。

4．g满足「∀viΦ」当且仅当g满足∀g＇(如果g’至多在gi上与g不同，那么g’满足Φ)。

(五)T(Lc的句子的真)

T(σ)当且仅当:(1)σ是一句子;(2)∀g(g满足σ)。

人们通常认为塔斯基对满足和递归技术的使用是他的真定义的两个最独特的特征。但是，应当注意的是这两个特征是由两个特定的语言事实所决定的。首先，标准的对象语言的语句是无限的，其次，在它的元语言中单独的每一语句是有穷长的。塔斯基本人曾经提出，如果他允许在元语言中的无限析取，那么同样的技术也应被标准语言保留下来。递归和可满足性就将会避免。

四 塔斯基语义学

(一)语义学和对应

对塔斯基而言，真是一个对应概念。但真不是唯一的一个对应概念。研究一般的对应概念的学科塔斯基称之为语义学。

大致的说，所谓语义学，我们理解为是关于那些表达语言表达式和被那些表达式所指称的对象和事态的关系的概念的总称［3］409-420。

像“指称”、“满足”和“定义”这些语义学概念直接表达对应关系:“珠穆朗玛峰”指称“喜马拉雅山的最高峰”;公式“x被谋杀”被约翰·肯尼迪所满足;表达式∃y(x=y2)(其中，“x”和“y”的论域是自然数)定义一集合{0、1、4、9、16，…}。像“真”这些其他的语义学概念表达了一种间接的对应。真是句子的一种性质，而不是真和对象之间的关系。而且只有在被这句子所指称的对象拥有归属于它们的性质时，给定的句子才为真。

(二)对应和间接引语

有些哲学家认为语义学概念是间接引语的概念:被引号引起来的概念有一种是真的性质当且仅当在这句子的引号消去之后，该语句为真［4］138-155。然而，塔斯基将这两种分析看作是相同的。

语义学概念的一个特有的特征是它们对某些表达式和这些表达式谈论的对象之间的关系给出了一种表达，或者通过这些关系的方式它们刻画了某些表达式或其他的对象类。我们也可以说这些概念有助于在表达式的名称和表达式本身之间建立一种关系［1］252。

我们能够以如下方式解释塔斯基的观点:存在着两种谈话模式，一种是对象的谈论模式，一种是语言的谈论模式。对应的思想能够以这两种模式加以表达。如

“雪是白的”是真的当且仅当雪是白的。

以及

“‘雪是白的’是真的”等于“雪是白的。”

在对象的谈话模式中，我们说一个将是白色的(物理)属性归结为(物理)对象雪的句子是真的当且仅当(物理)的对象雪有是白的(物理)属性。在语言学的谈论模式中，我们说一个将真(的语义学性质)归属于一句子，而这句子将白色归属到雪上去是等同于将白色归属于雪的句子。

(三)逻辑语义学

塔斯基语义学最重要的成就是他对于元逻辑概念(“逻辑后承”、“逻辑真”、“逻辑一致性”等)的定义。在完成了他的真研究之后，他将其注意力转向逻辑后承的研究。在塔斯基之前，逻辑后承是按照证明的术语定义的(句子σ是一句子的集合Γ的逻辑后承当且仅当存在着一个从一些句子Γ到σ的逻辑证明)。然而，哥德尔的不完全性定理表明“逻辑后承”的证明论定义是不充分的。并非所有的现代逻辑框架中的形式化理论都能够以所有的它们的真语句是能够从它们的公理中可证的方式被公理化。使用语义学和集合论这两种资源，塔斯基为形式语言发展出一种定义“逻辑后承”的一般方法。

(四)“逻辑后承”的语义学定义

σ是Γ的逻辑后承(在形式语言L中)当且仅当不存在一个(L)模型，在其中Γ的所有句子为真而σ为假。

这个定义(能够容易地转换为例如“逻辑真”、“逻辑一致性”等其他元概念的语义学定义)在将逻辑语义学或者模型论转化为当代逻辑的两个主要分支之一方面发挥了重要的作用。

五 塔斯基未回答的问题

塔斯基的著作是关于逻辑语义学的，但人们发现塔斯基对逻辑语义学，甚至对一般语义学的性质很少给出回答。特别是，塔斯基对逻辑词汇的作用、范围和性质，以及逻辑和非逻辑语义学之间的关系缺乏一种充分清晰的说明。

(一)关于逻辑词汇的问题

在塔斯基语义学中逻辑词汇的作用是至关重要的。句法结构以及经由满足的真理的递归定义是建立在与特定常项——同一性、真值函项连接词，存在和全称量词——相对应的固定的函项基础上的。通常人们一般认为这些常项是逻辑的，但是并没有人对比如说量词的选择提出直接的论证。在许多教科书中逻辑被刻画为“一般的”，“题材中立的”逻辑真理被刻画为是“必然的”。但是在一般性、中立性和必然性本身缺乏一个充分标准的情况下，我们会认为“并非”、“或者”、“所有的”和“有些”以及它们的派生是唯一地携带有一般、中立和必然的性质吗?

1936年塔斯基已经认识到逻辑词项的问题对语义学的重要性:

构成我们的整个(逻辑后承语义学定义)结构基础的是对所有的我们所讨论的语言划分为逻辑和非逻辑的。的确这种划分不是任意的。如果，比如说，我们将非逻辑记号包括在蕴涵，或者全称量词的范围之内，那么我们关于后承概念的定义将导致与普通使用明显相矛盾的后果。另一方面，我所知道的客观理由允许我们在两组术语间作出明确的区别。似乎我可能在逻辑词汇中包括了逻辑学家通常认为是非逻辑的词汇而没有遇到与普通的使用不一致的后果。在极端情况下我们可以把所有的语言中的词项看作是逻辑的［5］401-408。

塔斯基的极端情况是指逻辑后承和实质后承之间的边界已经消失的情况。那样一种实质有效后承的例子如“布什在1992年的总统选举中失败，因而克林顿成为1994年的美国总统”是逻辑有效的。为了避免这一结果，逻辑和非逻辑词项之间的区别的理由必须被确立。显然，确立这样一种区别对逻辑而言是最为重要的。若干年来逻辑哲学家致力于探讨逻辑和非逻辑词汇划分的标准，然而，这不是一个选择的问题，而是一个不知道如何着手确立合理的划分的问题。

(二)关于不提供信息性

塔斯基的真理的形式定义是内在的不提供信息的。本质上，这定义说的是“Ф”或者“ψ”是真的当且仅当“Ф”是真的或者“ψ”是真的，“有些x是Фx”是真的当且仅当在论域中的有些个体满足“Фx”等等。如果“或者”在“Ф或者ψ”中或者“有些”在“有些x是Фx”中是不清晰的，有歧义的或者不精确的，那么上述真理定义并不能够帮助我们抵御这种不清晰、歧义和模糊性。然而，对连接词而言，我们确有一个能够提供信息的定义，并使之与一个逻辑性的精确标准联系起来。在现代逻辑的早期阶段逻辑连接词的区别性特征被真值函项性所确立，建立在这一特征的基础上，逻辑连接词被认为等同于某些数学函项，即布尔真值函项(从真值序列到真值的函项)。语义学等同于布尔函项的逻辑连接词导致对逻辑连接词的下列标准:

(LC)一词项C是逻辑连接词当且仅存在着一自然数n和由布尔函项f c:{T，F}n→{T，F}使之对任意良构语句n-元组ɑ1，…，ɑn，「C(ɑ1，…，ɑn)」是一良构语句，它的真值是被f c［ν(ɑ1)，…，ν(ɑn)］所确定的，其中1≦i≦n，ν(ɑ1)是ɑi的真值。

这一标准对“什么是逻辑连接词?”问题给出了精确而又传递信息的回答。它确定了给定逻辑连接词选择的充分性(～和∨构成了完全的选择，但是∧和∨并没有构成完全的选择;因而，我们能够用～和∨定义所有的真值函项，但不能够用∧和∨定义所有的真值函项)。它使得我们能够对复合语句的真值条件给出更加富有信息性的说明。

与逻辑连接词不同，逻辑谓词和量词通常按照枚举的方式被定义，与将它们转换为口语相比元理论的说明做的较少。的确它们在数学中的使用使得这些词项的涵义变得精确，但是还没有一种系统的方式将逻辑谓词和量词认同为数学的函项，而后者有一种一般性的逻辑标准。

(三)关于逻辑语义学与一般语义学的关系

塔斯基真理的递归定义仅限于通过逻辑算子的方式生成的句子。按照这种定义每一逻辑词项获得一种特定的处理，但是所有的一给定语法范畴的非逻辑词项被“一同”处理。这自然就会提出是否塔斯基语义学是内在的合乎逻辑的问题。显然，逻辑关心的是逻辑结构对句子真值的贡献，但是逻辑结构并不是在句子的真或者假中的唯一因素。在何种程度上塔斯基的方法是限于逻辑语义学?我们能否认为自然语言语义学是塔斯基理论的一种直接扩展吗?

因而，以下问题有待于回答:(A)逻辑词汇和非逻辑词汇之间的区别有没有一种哲学基础? (B)我们能够为逻辑常项发展一种精确的数学标准，并在此基础上发展一种精确的传递信息的真理定义?(C)逻辑语义学和一般语义学的联系是什么?在1957年之前，前两个问题是难以作出回答的，因为尚不存在一种系统的逻辑词项的研究，但是由莫斯托夫斯基(Mostowski)标准量词的扩展改变了这一切。它创造了一个在其中发展、比较和研究逻辑词汇的框架。

六 对塔斯基理论的三种批评

尽管塔斯基的真理理论被广泛认为是20世纪分析哲学的主要成就，它的哲学意义仍被反复质疑。与以上(第5部分)问题相关联，批评主要来自以下几个方面:(A)塔斯基的语言分层论对说谎者悖论的解决只适用于人工语言，不适用于自然语言;(B)塔斯基对语言的真做出的是一种相对性的处理;(C)塔斯基的真理定义是平庸的。

(一)语言分层解决的限度

许多哲学家发现塔斯基对说谎者悖论解决的不尽人意之处在于，它不能使我们定义自然语言中的真概念。因为自然语言具有普遍性，因而这种语言是不一致的。

这些哲学家对塔斯基的下述警告置若罔闻:(1)因为自然语言的普遍性，因此给出自然语言的真理定义是不可能的;(2)语言分层的解决说明并且使自然语言许多片段中的“真”的使用合法化。这里的自然语言片段指的是所有的那些开放的并且能够被其结构是精确阐述的人工语言所表达的人工语言。例如，索姆斯拒绝了自然语言是不一致的主张［6］。其他的批判指出塔斯基的处理过于严格，他消除的不仅仅是话语中的“真”和其他相关概念(例如，“假”)的悖论式使用，而且也消除了这些概念的合法使用。例如，克里普克(Kripke，1975)的下述例子:考虑两句水门危机时说的话，其中一句由唐纳说出，另一句由尼克松说出:

A．尼克松关于水门事件所说的话都是假的。和B．唐纳关于水门事件所说的话都是假的。

这一语句对可以一致性地指派真值，然而塔斯基的真理理论没有为这种语句对保留存在的空间。按照塔斯基的理论A的语言层次的类型必须要比B高，而A的语言层次类型又要比B高，这是不可能的。

(二)平庸性和相对于语言性

通常人们将塔斯基的理论解释为一种还原主义理论，或者更具体地说，一个其理论的目的是将一给定语言中的真概念还原为这一语言的原子公式(非逻辑常项的指示条件)的满足条件。假定了一语言L，我们通过以下方式确定L中句子的真值:首先列出L的初始非逻辑常项的指称清单。进而在对语言L的真理定义中，应用递归“指令”到这些清单上。例如，如果L是一个具有两个初始非逻辑常项，个体常项“a”和1-位谓词P，P的外延是数1和一个指示所有偶自然数的集合。我们首先为L列出一个指示清单＜“a”，1＞和＜“P”，{0、2、4、6，…}＞。进而，在L的真理定义中，我们通过将递归规则应用于这些清单而计算出这些句子的真值: “Pa”(在L中的)是真的当且仅当1∈{0、2、4、6，…}，“～Pa”(在L中)是真的当且仅当“Pa”(在L中)是假的。即当且仅当1∉{0、2、4、6，…}等。

建立在这一分析基础之上的两个有影响的批评是:(1)塔斯基的真理定义是平庸的;(2)塔斯基的真理概念是相对于语言的。

1．关于琐屑性的批评。塔斯基语言L的真理定义将L中的真语句还原为L的原子公式的满足。但是他的满足的原子公式是完全不提供信息的。它并不是依据一对象(或对象的n-元组)满足一给定的原子公式来识别定义的特征，而是一对象满足一原子公式当且仅当它属于某一序列(在上面的例子中，“Pa”是真的当且仅当它属于0、2、4，…)。但是这种类型的定义是一种依靠枚举的定义(“x是P当且仅当x是0，或者x是2，或者x是4，…”)。因此它缺乏信息值。

菲尔德(Field)清楚地阐述了这样一种批评［7］69;347-375。菲德尔将塔斯基的满足定义比拟为科学概念中的枚举定义。例如，考虑概念效价的枚举定义:

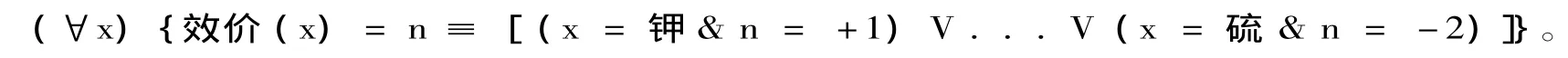
化学元素的效价是表达物理属性的元素化学组合的整体。一个联系到元素化学性质的效价具有较高的信息度;另一方面，由枚举而来的定义是完全琐屑的。(通过使用递归条目从化学元素到化学元素的配置的扩展定义将不可能改变下述情况:如果“基础”是平庸的，作为定义整体上也是平庸的。)

尽管菲尔德特别关心塔斯基将语义学概念成功地还原为非语义学(特别是，物理学家的)概念的一方面，他的批评并不限于这一方面。菲尔德说，在哲学中的标准使用不应当比在其他科学中的那些使用要低，靠枚举定义真理是没有任何哲学重要性的［7］369。

2．相对性的批评。对塔斯基理论的另一种批评涉及真理对语言的相对性。论证概述如下:塔斯基的方法产生了一个对特定语言的定义。在那里，对一给定语言的真概念是建立在对那种语言的指示详加说明的清单基础上的(即一个不可能服务于任何其他语言的真理定义的清单)。基于这种理由，塔斯基的真理概念是相对于语言的［8］。塔斯基定义的并不是一个绝对的“真”概念。在“L中的真”概念没有任何哲学上的重要性。

七 塔斯基理论的重新解释

(一)对真的收缩主义的处理

塔斯基的真理定义基本主题所呈现出的非提供信息性的观点使得一些哲学家致力于研究一种建立在提供信息基础上的塔斯基真理定义。菲尔德建议放弃使用作为真理定义基础的指称清单，而使用一个一般的、指称的和提供信息的理论作为基础。菲尔德指出克里普克的指称的因果历史的概述是一个很有希望的起点。但是关于一种普遍和提供信息的理论的发展充满了困难，这使得菲尔德和其他一些人将研究方向转向真理的紧缩主义或者极小主义。

以下观点反应了紧缩主义的态度:

真被一种初始的平庸性［每一个命题说明了它自身是真的真值条件(例如，命题雪是白的是真的当且仅当雪是白的)完全捕捉到［9］ix。

与其他性质不同，对科学分析和概念而言，“是真的”是一个值得怀疑的概念［9］6。

真理理论比起无争议的等同模式的例子并不含有更多的内容。

(E)p是真的当且仅当p［9］6-7。

尽管紧缩主义者在许多问题上有所不同，但是大多数紧缩论者认为与塔斯基的理论相比，真理理论不需要提供更多的信息。一些人希望将塔斯基的真理定义扩展到更大范围的语言结构:索引词、副词、命题态度、模态算子，等等。但并不要求一个更加实质性的分析。按照紧缩主义的观点，传统上人们一直试图将真的本质识别为所有的真定义共有的特定的性质——这是一个伪问题，所有的真理并没有一个实质上共同的称谓。真理理论的任务是产生一个所有的等同模式的实例的清单，而不考虑这个清单是如何产生的。真理理论仍是一个平庸的汇集。

(二)紧缩主义处理的批评

真理的紧缩主义处理是建立在理论的传统概念基础上的:一概念X的理论是一个归属为X之下的所有对象公分母的一种理论。如果所有这些对象的公分母是琐屑的，那么X也是琐屑的，且X的理论是一个琐屑的汇集。然而，这样一个哲学理论的概念是建立在缺乏根据的假定——即一给定概念X的内容是所有X的实例的公分母——基础上的。显然，某些概念的内容并不被它们实例的公分母所穷尽的，或者接近于被穷尽的。例如，游戏的概念就属于这种情况。然而，如果“游戏”并不是一个公分母的概念。显然它并不是空洞的或者是不足道的概念。游戏理论既不是空洞的又不是平庸的。一种游戏理论可能不会被整个地压缩为一个单一的原则，被一个单一的公式所表达，而是它以一种一般地和提供信息的方式，识别出若干管辖游戏和描述它们的性质、工作原理、相互关系和后承的若干原理。

(三)塔斯基的理论实际完成的是什么?

然而，不论是辩护者还是批评者都认为塔斯基的真理定义是对逻辑科学做出的实质性贡献。显然塔斯基的理论并没有对其他的学科做出类似的贡献。尽管塔斯基为L语言的真定义产生了一个逻辑后承的定义，但是它并没有为L产生一个认识论的，或者模态的、物理的或者生物学的后承概念。(后者例如，“A知道P，所以A相信P”;“必然P，所以可能P”;“在时间t作用于物体a上的力是零，因而在时间t，a的加速度为零”;“a是一位女性，所以a没有Y染色体”等。)为什么塔斯基的真理理论会产生一个逻辑后承的说明，而不是其他后承类型的说明?为了产生一个类型X的逻辑后承，而不是其他类型的后承说明，一个真理理论应当具有何种特征?

对这些问题的回答是十分清楚的。一个后承关系是一个真保持关系。如果C与一语句的集合Г有后承关系R，且如果Г的句子都是真的，那么它们的真通过R是可保持的(或者通过R被传递到C)。如果R是一个类型X的后承关系，那么真的保持归咎于Г和X的句子的X-结构，即归结于在这些句子中的和X的常项的内容和组织。因而如果C与Г有逻辑后承关系，这是由于所涉及句子的逻辑结构;如果C与Г有一种模态的、认识论的、物理的，或者生物学的后承关系，这是由于那些句子的模态的、认识论的、物理学的或者生物的结构。为了为一种语言L产生一个类型X的后承的定义，一个L的真理定义必须说明X结构对L句子真值的贡献，塔斯基对L语言的真理定义与L的句子的逻辑结构是协调的，因而它形成了L的逻辑后承概念。

这一事实说明，塔斯基实际所完成的是对真的逻辑结构的贡献的说明。塔斯基的理论告诉我们一给定句子的逻辑结构如何影响它的真值，而没有告诉我们其他的句子结构类型(模态的、物理的，…)如何影响它的真值。按照这种解释，塔斯基的理论仍是一个特定的理论，尽管它具有真理的基本和一般的成分，即它的逻辑成分。它的目的仍是以一种穷尽的、系统的、传递信息的方式描述归咎于它们的逻辑结构的句子的真值条件。这一解释说明了为什么塔斯基的真理理论在逻辑上如此重要和富有成效。更进一步的，它使塔斯基的免于相对主义和琐屑性的批评。

(四)再论相对性

尽管塔斯基在确定句子的真值条件时，使句子的非逻辑成分起作用的方式是相对于语言的，但是逻辑成分的作用却不是如此。非逻辑常项的指示清单随着塔斯基语言的不同而不同。但是逻辑常项的语义规则却是跨语言而保持不变的。塔斯基的一给定语言的逻辑结构的公式和非逻辑结构的公式之间的不同是规则和应用之间的不同。比如说，为了计算出一种塔斯基语言的句子“约翰爱玛丽并且约翰爱詹妮”的真值，我们采取联系到(塔斯基方法中的)“并且”的固定的真值条件，并且将它应用于在L中的“约翰爱玛丽”和“约翰爱詹妮”的真值条件。我们可以说管辖对真的逻辑结构贡献的原理是绝对的;而它们的实例(应用)则是相对于语言的。

但是任何理论都有这种情况，比如说加法的规则在所有的算术应用中都是相同的，但是在生物学中，这种规则运算于生物实体的集合，而在理论物理中它运算于抽象实体的集合。

(五)再论平庸性

如同相对性一样，平庸性也直接地指向塔斯基的真的非逻辑成分的处理。以塔斯基给定语言L的真定义为例，塔斯基认为对公式和L中的非逻辑词项的满足和指示条件通过枚举的方式给出，这样的一个结果就是整个定义的平庸性。尽管这一批评对塔斯基理论(涉及本篇第5部分)而言是有根据的，但对于目前的解释而言它是不正当的。按照第一种解释，塔斯基的理论是还原主义的理论。它的任务是对一给定的语言将真概念还原为它的非逻辑结构公式和它的非逻辑常项的满足和指示条件。如此这般，非提供信息的责任应由它的非逻辑条目负责。因为这些是平庸的，作为一个整体的定义是平庸的。但是，第二个方面，按照逻辑的解释，非提供信息的责任要由逻辑条目加以承担(非逻辑条目仅起一种辅助性作用)这样逻辑的条目是提供信息的，且真理的定义也是传递信息的。

在塔斯基的定义中逻辑条目是提供信息的吗?为了提供信息，逻辑条目不能够只靠枚举，而必须描述联系到建立在原理基础上的不同的逻辑结构的真值条件。现在按照第一种解释，塔斯基的真定义并不是真正提供信息的。以逻辑连接词为例，否定和析取的条目本质上说的是“非σ”是真的当且仅当不是真的，“σ或者ζ”是真的当且仅当σ是真的或者ζ是真的。这些款项并没有解释“并非”和“或者”的满足条件;它们把这一切看作是给定的。(定义中的“并非”仅仅是重复了在被定义项中的“并非”。)按照一种更宽泛的解释，我们可以把逻辑连接词条目看作是隐含地指称这些连接词说明的提供信息的布尔或真值函项。布尔说明提供了(1)连接词的逻辑性提供信息的标准，(2)每一个建立在这些标准之上的逻辑连接词的满足条件的系统刻画。依据这种刻画，否定被1-位布尔函项f所刻画;f的定义是f(T)=F且f(F)=T。析取被2-位函项f所刻画，f的定义是f(T，T)=f(T，F)=f(F，T)=T，且f(F，F)=F。这些定义是精确的和传递信息的。在1933年，并不存在着一个逻辑谓词和量词的类似标准，但是在此后的几年，建立在它的基础之上的个性化逻辑谓词和量词的满足条件的系统刻画已经发展起来。因而，今天我们有可能将塔斯基的真理定义扩展到包含有满足这一标准的任何逻辑常项的语言，并且为逻辑常项构造满足的条目，进而避免平庸性的批评。

八 逻辑和非逻辑词汇区别的哲学基础

逻辑的主要任务之一是阐明逻辑后承关系。但是假定了这一概念，一个问题就立刻出现了:“何种后承关系是逻辑的后承关系?”人们会说后承关系与句子的逻辑结构有关，其中结构是一个特定的逻辑词项表达和它们的排列的函项。因而，蒯因说:“逻辑蕴涵(后承)是完全建立在真值函项、量词和变元的如何排列组合的基础上的。是完全建立所涉及的句子的逻辑结构基础上的”［10］48。然而，这又引出了下一个问题:“何种词项是逻辑词项?(已给定句子的逻辑结构是什么?)”所以，从我们目前(进入到逻辑词汇概念的探讨)的观点来看这种处理是毫无希望的。为了区别逻辑词汇我们需要逻辑后承的直觉刻画，而对后者的刻画应独立于对逻辑词汇的区别。

满足这一要求的逻辑后承的刻画是由塔斯基在“论逻辑后承概念”一文中给出的。按照塔斯基，一后承是逻辑的当且仅当它满足两个基本条件:(a)必然性和(b)形式性。用塔斯基的话来说“一个直觉性质的某些考虑将形成我们的起点”。考虑任意句子类K，以及一从K类句子推出的句子X。直觉上绝不可能出现下述情况，即K类句子为真而句子X为假。更进一步地说，我们这里所涉及的是逻辑的概念，即形式后承。在某些逻辑后承的说明中有人认为是必然性而不是形式性是逻辑后承的主要性质。但是塔斯基认为这些性质未能说明逻辑后承与其他后承的区别性特征。与仅仅是必然性相比，逻辑后承满足更强的条件:逻辑后承是形式的且是必然的，因而是形式必然的。

如果我们以塔斯基的描述作为我们讨论问题的起点，我们首先要对形式性略作一些说明。通常认为形式性是一句法条件:逻辑后承的形式性被各种句法定义所捕捉，而它的必然性则被语义学定义所捕捉。这种处理是有缺陷的，逻辑后承的直觉概念包括了逻辑后承在一种特定方式中，即形式方式中是必然的思想。两个直觉上是必然的但却并非是形式后承的例子如(1)“所有的球是蓝色的，因而它不是黄色的。”和(2)“约翰是单身汉，因而他是未婚的。”显然，这些推理是建立在非形式原理基础之上的。(1)是建立在形而上学—物理学原理基础上的，(2)是建立在词汇约定基础上的。这一事实决定了我们为什么不把它们看作是严格的逻辑的原因。

塔斯基例举了两个逻辑后承的句法定义，并且发现它们缺乏:标准的证明论的定义，以及一个替代定义。先从证明论的定义开始。在现代的术语中我们能够用公式表示这一定义:给定一标准的一阶逻辑，或者高阶逻辑。逻辑L具有公理集合A以及规则的集合R。如果Г是一的L的句子的集合，σ是L的句子，那么σ是Г的逻辑后承当且仅当存在着一个从Г到σ(使用L中的公理A和推理规则R)的证明。现在，考虑一个表达在一阶或者高阶逻辑中的“P(0)，P(1)，…，P(n)，…，因而，所有的自然数有性质P”的推理。这一推理直觉上看是形式的又是必然的，然而它不能被标准的证明方法所确立。

第二个逻辑后承的句法定义是替代。这定义说给定一(解释的)语言L，σ是Г的逻辑后承当且仅当对L中的主要非逻辑成分不存在一个统一的替代，使得所有的Г语句为真而σ语句为假。关于这一定义存在着三个问题:塔斯基在1936中指出了第一个问题，其余两个问题能够从艾切曼迪的论文分析中得到［11］。

(ⅰ)替代式定义对非逻辑词汇的丰富性过于敏感。如果L有一个有限的非逻辑词汇，那么，某些不能通过直觉检验的后承可能会通过替代式的检验。例如，令“塔斯基”、“哥德尔”、“是一个逻辑学家”和“是一个男人”是L中仅有的非逻辑词汇。推理“塔斯基是个男人，因而，塔斯基是个逻辑学家”是逻辑有效的，但直觉上是不正确的。

(ⅱ)替代式方法并没有区别逻辑和非逻辑词汇的资源。它的仅有的区别性资源是语法，词汇和替代下的实质真的保持。这些对于决定一给定词项的逻辑地位是不充分的。因而，替代性方法将逻辑和非逻辑词项的区别还原为“固定的”和“非固定的”词项之间的区别，而逻辑后承概念是相对于固定词汇和非固定词汇这种具有任意性的划分的，也容易看出相对于某些固定词项的选择的，“错误”的后承通过了替代性检验，而相对于其他的词汇，“正确”的后承又没有通过检验。

(ⅲ)替代式方法仅考虑现实世界。按照替代式定义一句子是逻辑真的当且仅当所有它的替代事例为真—即在实际世界的真。因而，从替代理论的观点看，逻辑真是在语言的替代实例下实际的保值真的。由此推出如果一个非形式、非必然的真对语言中的非固定词汇不敏感，特别是，如果该语言并不包含非固定词汇，它就自动判定是逻辑的真。即便是按照逻辑词项的标准选择这一问题也会发生。“存在着至少两个对象”可被纯粹的逻辑词汇(□x□y(x≠y))表达，因而它的真等同于它的逻辑的真。这个例子是逻辑的不确定性的一个范例。不难看出对于逻辑后承而言，这样的情况也会出现。

塔斯基拒绝了证明论和替代定义，决定使用一种不同的方法。对他而言这种方法自然是由他发展起来的语义学方法。以下我们呈现塔斯基理论的一种表述形式，该形式表明关于这一理论动机的思考提供了对林德斯特仑(Lindstrom)标准的一种哲学基础，以及在假定了这一标准的前提下，理论如何避免证明论和替代式定义的局限和陷阱［12］32;186-195。

什么是一种语义学理论，遵循着塔斯基的教诲，人们认为语义学理论是处理将语言和世界相联系的概念的。存在着两种类型的语义学概念:一种是直接地满足上述特征的概念，一种是间接地满足上述特征的概念。“指称”和“满足”属于第一种，“真”和“逻辑后承”属于第二种。“指称”是词项和它指称的对象之间的一种关系;满足是公式和满足该公式的对象之间的一种关系(对象序列，一个从语言中的变元到在论域中的对象的函项)。然而，真和逻辑后承是语义学性质(关系)的:真是句子的一种性质，逻辑后承是一句子与句子的集合之间的关系。为什么我们将其看作是语义学概念呢?通常的回答是它们之所以是语义学概念是因为它们是按照语义关系(指称和满足)可定义的。但是这一回答是本末倒置了。真按照指称和满足来定义，因为它必须利用对象和它们与语言的关系。对一给定的语句s享有或者不享有真，当且仅当在s中被指称的对象拥有被s所归属于它们的性质(或者所处的关系)。更一般地说，一语言学的性质是语义学的当且仅当由于某些关于被在e中指称的对象的事实，而使它享有一给定的语言学实体;这对关系而言也是如此。进而，把逻辑后承作为一种语义关系，就是把它作为语言学实体之间的关系，这种语言学实体是建立在被这些实体所指称的对象之间的关系基础上的。语义学将关于语言的陈述还原为关于对象的陈述。这里，我们不可能讨论“真”的还原，但是在“逻辑后承”的情况下，语义学将“句子σ是句子集合Г的逻辑后承”还原为类似于“将归属于由σ所处的(对象)关系R的性质，还原到归属于由Г所处的对象的性质”这样的东西。因而，为了理解作为逻辑关系的语义后承的逻辑性质就是理解(ⅰ)指称的性质，和(ⅱ)对象关系R的性质。将指称问题先放一边，我们能够将关于逻辑后承的直觉条件—必然性和形式性视为关于R关系。必然性要求R必然地成立，形式性要求R只考虑所涉及对象和性质的形式特征。什么是对象关系R呢?

让我们看一个直觉上逻辑有效的推理(1)“有些东西是白色的并且是可口的，因而有些东西是可口的。”为什么(1)是逻辑有效的呢?借鉴莫斯托夫斯基(Mostowski，1957)的处理量词的方式，我们可以说(1)是逻辑的有效的，因为(ⅰ)它的前提说白和可口的事物的集合的交集是一非空集，(ⅱ)它的结论说交集的一个，即可口的事物的集合是非空的，(ⅲ)当一个集合的交集是非空的，交集的每一个也是非空的。

在《逻辑哲学论》中维特根斯坦似乎拒绝了这种考察逻辑后承的方式。维特根斯坦说“逻辑命题的标志不是一般有效性，对所有事物而言，一般并不意味着比偶然有效要多。”这一观察使维特根斯坦拒绝了将逻辑还原为一般性的观点，类似的拒绝也发生在艾切曼迪(1990)那里。但是维特根斯坦的问题并没有出现于我们的分析中;逻辑后承并不是可还原为任意一种普遍性，逻辑后承是可还原为一种特殊的一般性，还原为可满足必然性和形式性直觉约束的一般性。必然性和形式性二者共同制约着函数F和“无论何时”的范围。形式性要求逻辑后承只依赖于所涉对象的形式特征(集合与交集的非空)，不依赖于实质性特征(白色和事物的味道)，必然性要求“每当”并不限于任何特定的论域，而是涉及所有可能的论域。将形式性与必然性组合在一起，我们可以说逻辑后承可还原为形式一般性，它是一种形式的普遍事实，(一种在对象的所有形式上可能的结构中都成立的事实)如果一个集合的交集是非空的，那么交集的集合的每一个也是非空的，它可归因于这一形式的和必然的事实(1)是逻辑的，即形式的和必然的有效。

塔斯基的语义学系统化了逻辑真和逻辑后承还原为形式普遍性的处理。那么在这一还原中逻辑词项的作用是什么。以(1)为例，构成(1)的形式关系并不受“白色”和“可口的”的外延变化的影响，而是受“某物”和“和”的外延的改变的影响。我们能够按照构成(1)的形式关系成立与“白色的”和“可口的”指称的个体集合是什么无关的，来解释两对词项之间的不同。给定任何形式上可能的个体域和该域中任意两个体的集合，如果两个集合的交集是非空的，每一个集合也是非空的。但是这对于合(unions)并不成立:形式上有可能两个集合是非空的，而其中的一个集合是空的。同样，两个集合的交集可能是空的，而其中的任何一个却是非空的，这在形式上也是完全有可能的。这就是(1)的有效性依赖于“并且”和“有些事物”的理由。如果我们用“或者”的外延替代“并且”的外延，或者用“无任何事物”的外延替代“有些事物”的外延，(1)就是逻辑非有效的。在(「…x…并且—x—」)中的“并且”指称一交集，“有些事物”指称是非空的性质，管辖交集和非空集的法则在所有的形式可能的结构中成立。

因而，在塔斯基的逻辑中逻辑词汇的作用是标记形式特征和对象的结构。特征和结构的类型对逻辑后承负有真正的责任。因为逻辑词汇在所有的对象的形式可能的结构中有指称，逻辑词汇是“普遍”词汇，指称性质的词汇应用于所有的形式可能的对象:人、狗、细胞、原子、颜色、自然数等等标准的逻辑词汇满足这些要求，因而，建立在这些词汇基础上的后承真正的逻辑的。但是，这自然就出现了一个问题，是否所有的形式必然的后承都是建立在标准的逻辑词汇的基础上的。以以下推理为例(1)“恰好有一个人;因而，存在有有限多个人，”和(2)“恰好有一个人;因而，至多有十个人。”在一阶逻辑中(2)被视为逻辑有效，而(1)则被认为是逻辑上不确定的。但(1)比(2)有较少的形式必然性吗?一个单元素集是无穷的比起它包括了十个元素在直觉上是更有可能的吗?

按照一般的理解，塔斯基语义学的任务是为发现逻辑的，即形式和必然后承提供一个完整的系统。达到这一结果的一种方式是通过转向标准高阶逻辑，但是，另外一种方式是通过增加新的逻辑词汇(例如，量词“存在着有穷多个x”)而扩展一阶逻辑。我们如何能够确定逻辑词汇的总体。确定逻辑词汇的总体就是确定对象的形式结构的总体。每一个形式结构是一些逻辑词项的扩展。每一个逻辑词汇指称一个形式结构。为了识别形式结构我们将使用最好的可用的普遍的形式结构的理论(一个可用于任何种类个体的结构)。目前来看，策梅洛的ZF，或者它的变体似乎是一个合理的选择。建立在这一标准的基础之上，我们说一词项是逻辑的当且仅当它在形式等同的结构之间不做区别。这也可理解为一词项是逻辑的当且仅当它不区别它的论元的同态性外延。建立在这一标准基础上，所有的基数量词是逻辑的，是一个对称关系的2阶性质是逻辑的，等等。更一般地说，任何一个作为高阶词项的可定义的数学词项本质上说逻辑的。例如，“两个”这个词项。作为个体词项的“两个”指称有特定个体—数“2”—因而它不是一逻辑词项，但作为一高阶词项“2”指称有性质结构—所有的与{0，1}的同态的集合—因而是一个真正的逻辑词项(这一比较解释了为什么个体常项并不包括在(L)中:个体常项指称原子对象，它们是没有结构的、形式的或非形式的对象)。

作为普遍和形式的逻辑词项的刻画允许我们解释塔斯基语义学如何避免替代性语义学的障碍，即它的固定词汇的任选的后承概念的相对性:林德斯特仑的标准排除了任何非形式的或者非普遍词项(“塔斯基”、“是一位逻辑学家”)作为逻辑词项的使用，排除了因持有这样的固定词项而获得的推理。两个其余的问题是通过引入塔斯基的模型和它们的特定特征而得以规避。在塔斯基语义学中，模型形式地代表了对象的可能结构，在所有的模型中真的概念并不是或者依赖于非逻辑词汇的规模或者实际世界的大小:是否“塔斯基”是L的仅有的单一词项或者不是，是否在不同的语言L的模型中，“塔斯基”被指派给如此众多不同的个体，以至于足以确立对“塔斯基是X”的反例。同样，在塔斯基模型中的真并不是在实际世界中的真，而是在一形式可能的结构中的真，形式上可能结构的概念并不受限于偶然的事实。

九 塔斯基语义学的逻辑性质

塔斯基语义学是专门设计用于逻辑的需要，或者同一个装置能够被用于解释语言和世界之间的关系的其他方面的吗?对这一问题的回答涉及众多问题，我们在这里只指出两个方面，在这两个方面塔斯基语义学是内在逻辑的:(a)它的“固定”词项的选择，(b)它的表征对象和事态的方法。第一点现在看来是明显的:塔斯基的语义学，甚至塔斯基的真理的一般定义是限于那些“被固定的”词汇是逻辑的语言，经由“满足”的递归的真定义反映了这一事实。这个定义使用了对应于语言的逻辑词项的固定的函项，这些函项仅考虑在它的论域中的对象的形式特征。第二个必须处理的问题是在塔斯基语义学中被刻画的对象和事态的方式，即处理它的模型的装置。我们可以简要地将其刻画如下:作为一种逻辑语义学，塔斯基的兴趣在于而且仅在于对逻辑后承有所贡献的那些对象和事态的刻画。也就是说，塔斯基的语义学是关于对象和事态的(普遍的)形式特征的描述，与其他目的无关。塔斯基模型不考虑对象的多样性和它们所拥有的非形式性质的多样性，所有东西不管是物理的还是精神的，是具体的还是抽象的，是微观的还是宏观的，是虚构的还是实在的，它们统统被视为一个集合的理论实体的元素。所有的这些多样性对象的性质被作为论域中的元素的集合看待，所有的关系被视为论域的元素的n-元组的集合，等等。塔斯基将对象所拥有的多重性质和所处的多种关系还原为一个单一的集合的元素的形式关系，尽管事实上一个对象拥有，比如说，一种道德的性质(例如，是善良的)，或者一个命题态度的性质(例如，希望成为一名总统)。塔斯基语义学对于这些差异并不感兴趣。集合的元素对于拥有一种形式的性质是充分的，对于塔斯基语义学的目的也是充分的。不需要对一些事物作出更精心的阐述，从塔斯基语义学的观点看，只有“对象x拥有性质P”的形式构架是基本的，也是他所关心的。

本文重点讨论了三个问题:(1)逻辑词汇和非逻辑词汇之间的区别有一种哲学的基础吗? (2)我们能够发展出建立在(1)之上的逻辑词汇的结构性定义吗?(3)在何种程度上现代语义学与逻辑关联在一起。本文对(1)和(2)问题提供了正面回答的一个概要，这也包含了对(3)的一些考虑。现代语义学从一种富有特质的逻辑语义学中发展出来。这一概念最初发源于塔斯基1930年的真理和逻辑后承的理论，随着逻辑词汇的扩展这种语义学也得到了极大的扩展。我们已经表明林德斯特仑做出的逻辑与非逻辑词项之间的区分有一种哲学的基础。我们也给出了在逻辑连接词的布尔代数定义之后对逻辑词项的一种结构性的处理。就现代语义学许多分支及其发展来看，在一定程度上它们是塔斯基语义学的一个副产品，或者是它的一个自然结果。它们都根植涉及语言和世界之间关系的逻辑理论之中。不管语义学最终将会走向何方，它与逻辑的联系始终是一个人们关心的问题。

［1］Tarski A．The concept of truth in formalized languages［M］．In Tarski，1933．

［2］Aristotle．Metaphysics［M］．The Basic Works of Aristotle，ed．R．Mckeon．New York:Random House，1941．

［3］Tarski A．On the concept of logical consequence［M］．In Tarski，1936．

［4］Ramsey F．(1927)Facts and propositions．The Foundations of Mathematics［M］．Paterson，NJ:Littlefield，Adams，1960．

［5］Tarski A．The establishment of scientific semantics［M］．In Tarski，1936．

［6］Somes S．Understanding Truth［M］．New York:Ofxford University Press，1999．

［7］Field H．Tarski’s theory of truth［J］．Journal of Philosophy，1972．

［8］Blackburn S．Spreading the World:Groundings in the Philosophy of Language［M］．Oxford:Oxford Universitly Press，1984．

［9］Horwich P．Truth［M］．Oxford:Basil Blackwell，1990．

［10］Quine Philosophy of logic［M］．Englewood Cliffs:Prentice-Hall，1970．

［11］Etchemendy J．The Concept of Logical Consequence［M］．Cambridge，MA;Harvard University Press．1999．

［12］Lindstrom P．First order predicated with generalized quantifiers［J］．Theoria，1996．

【责任编辑陈雷】

Tarski’s Definition of Truth，Semantics and Logical Consequencel

ZHU Jian-ping

(School of Politics and Administration，Suzhou Univ．，Jiangsu，Suzhou，215123，China)

Tarski’s seminal work on truth and logical consequence is the most important contribution to modern semantics．The recursive definition of truth in terms of satisfaction and the inductive，step-by-step definition of logical syntax on which it is based，the notion of semantic model，the definitions of logical thrth and logical consequence，are the core of contemporary semantic theories．Model-theoretic semantics，possible world semantics，theories of meaning such as Davidson’s and Montague’semantics and even logical form，all incorporate Tarskian Principles．

Tarski;definition of truth;semantics;logical consequence

B81

A

1006-1398(2014)02-0056-15

一 语义学:一个塔斯基的论题

如果我们按照他对当代科学和哲学公认的贡献，可以说，存在着三个阿尔弗雷德·塔斯基。一个是纯粹意义上的数学家，异乎寻常清晰的逻辑学家和模型论之父。这种身份的塔斯基是一位知名的逻辑学家和有着鲜明形式倾向的哲学家。第二个塔斯基是继卡茨米尔、特瓦尔科夫斯基、莱斯尼威斯基、鲁卡谢维奇、埃杜凯威茨等之后华沙哲学学派最杰出的成员，一个与希尔伯特的形式主义和维也纳学派的实证主义有着最为密切联系的哲学家。第三个塔斯基是英语世界中的主流语言哲学家，这方面的威望来自于他所提出的真概念的定义，以及以某种方式被戴维森运用于意义理论研究的塔斯基语义学思想。这种类型的塔斯基告诉我们诸如“‘雪是白的’当且仅当雪是白的”这种语句对于真理论是非常重要的，进而塔斯基也对说谎者悖论提出了一种解决，他还首次提出了自然语言的“不一致性”问题［1］252-278。

本文关注的是第三种类型的塔斯基。就此而论，从历史上看我们可以区别塔斯基语义学理论的两个目标:一个是哲学的目标，一个是元数学的目标。塔斯基的哲学目标是提供一个真的普通概念，即在科学、数学和日常话语中通常使用的真概念的定义。按照这种真定义，一句子的真在于句子与实在相一致。这是一个以亚里士多德的真理观为出发点的定义。按照亚里士多德:“某物是什么而说它不是什么，或者某物不是什么而说它是什么为假，而某物是什么说它是什么，或者某物不是什么而说它不是什么为真”［2］1011b25。其基本目标就是建构一个能够捕捉并赋予这一概念精确内容的定义。

2013-10-14

朱建平(1956-)，男，山东济南人，哲学博士，教授。主要从事逻辑哲学、逻辑史、内涵逻辑及语言哲学和心灵哲学研究。