L形异型材共挤胀大及变形的三维非等温数值模拟

何建涛，柳和生＊，黄兴元，黄益宾，邓小珍

（1.南昌大学机电工程学院聚合物成型实验室，江西 南昌330031；2.上饶师范学院物理与电子信息学院，江西 上饶334001）

0 前言

共挤出技术是用2台或2台以上挤出机将2种或多种聚合物在一个复合机头内汇合共挤出得到多层复合制品的加工过程[1]。共挤成型技术是一种先进的挤出成型方法，其具有不需黏结或贴合、效率高、成本低等优点，因此该技术已广泛应用于复合薄膜、板材、管材、异型材和电缆的生产[2]。共挤制品各层厚度的均匀性以及分层界面的稳定性是评价共挤制品品质的重要指标，然而在共挤过程中除存在单组分挤出过程出现的挤出胀大、熔体破裂、“鲨鱼皮”等现象外，还存在黏性包围、分层界面不稳定等现象[3-5]，这不仅影响共挤制品的品质，也使得共挤口模的设计与加工更复杂。目前，国内外学者对圆形、矩形共挤研究比较多[6-7]，针对异型材共挤研究比较少。本文通过对L形双层共挤异型材进行三维非等温共挤数值模拟，对比分析了L形分层共挤时，PP和PS 2种材料不同组合下口模出口面速度场、剪切速率场的分布以及共挤出胀大和变形情况。

1 数值研究方法

1.1 几何模型和有限元模型

该模型为L形双层共挤异型材，2层熔体的厚度相等，为缩短计算时间，忽略2种熔体汇料前的单独流动区域，只考虑共挤出流道区和共挤出胀大区2个区域。MNPQRO为共挤出口模入口面，GHIJKL为共挤出口模出口面，几何模型如图1所示。

该模型结构简单，形状规则，故采用8节点6面体单元来划分网格。为了验证网格数量的合理性，本文建立了3个网格模型，粗糙网格（M1），中等网格（M2），精细网格（M3）。因熔体在口模出口附近流场变化较大，故在口模出口附近适当加密网格，图2为有限元网格模型。

1.2 数学模型

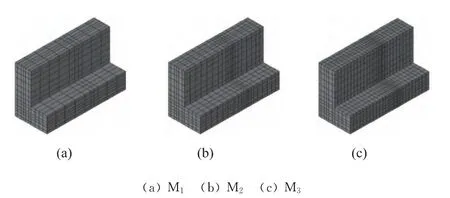
图2 有限元网格模型Fig.2 Finite element meshes for numerical simulation

本文假设2种聚合物均不可压缩，熔体间互不相溶，流动为非等温稳态流动，由于聚合物的高黏性，故忽略重力和惯性力的影响。在以上假设下，流场的控制方程为：

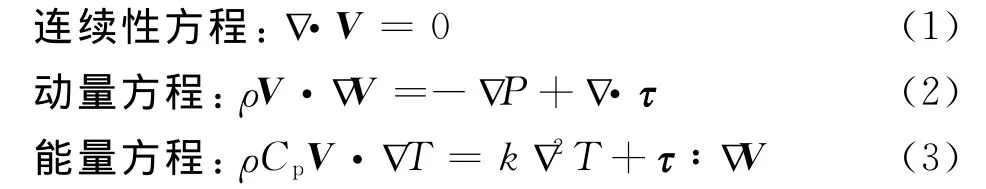
式中 V:速度矢量，m/s

∇:哈密尔顿算子

ρ:熔体密度，kg/m3

P:熔体静压力，Pa

τ:偏应力张量，Pa

Cp:熔体定压比热容，J/（kg·K）

T:熔体温度，K

k:熔体热导率，W/（m·K）

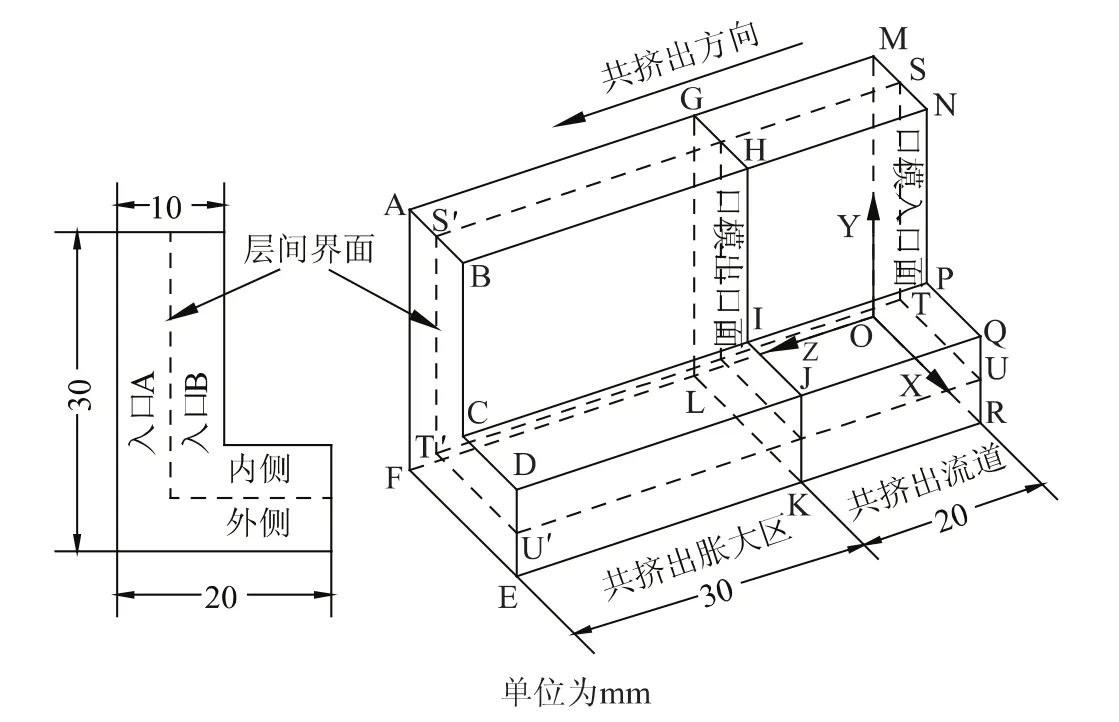
图1 数值模拟几何模型Fig.1 Geometry model for numerical simulation

1.3 本构方程

本文使用能反映聚合物黏弹性且易收敛的PTT本构模型[8]，其方程为：

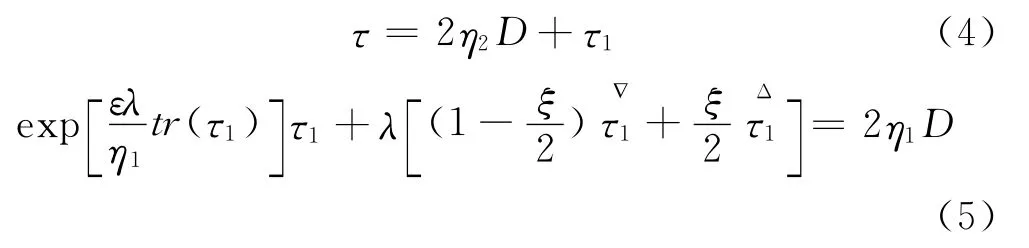
式中 η1、η2:零剪切黏度中弹性和黏性分量，Pa·s

D:形变速率张量，s-1

λ:松弛时间，s

ε:和拉伸特性相关的参数

ξ:和剪切黏度相关的参数

τ1:偏应力张量中弹性分量，Pa

τ1上的符号Δ:下随体时间导数

τ1上的符号∇:上随体时间导数

非等温条件下，考虑黏性生热对黏度的影响，温度对黏度的影响采用Arrhenius方程来描述[9]：

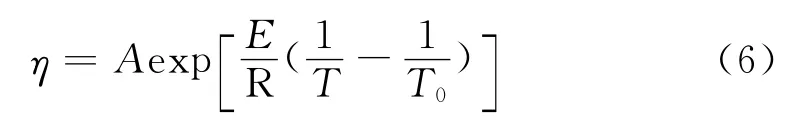
式中 η:黏度，Pa·s

A:参考温度T0时的零剪切黏度，Pa·s

E:熔体活化能，kJ/mol

R:气体常数，8.32 J/（mol·K）

T0:参考温度，K

T:熔体温度，K

1.4 材料物性参数

模拟所用材料为PP和PS，挤出温度为473 K，参照文献[7]设置 PTT 本构参数，同时参照文献[10-11]设置材料的其他参数，具体参数见表1。

1.5 边界条件

分别用fn，fs表示边界面的法向应力和切向应力，用vn，vs表示边界面的法向速度和切向速度，不考虑熔体与周围环境的热交换。

表1 材料参数Tab.1 The material parameters

（1）口模入口面

MSTURO和SNPQUT分别为入口A和入口B，2入口进入的聚合物熔体分别称为外侧熔体和内侧熔体，图1中已标示出。两入口的体积流率分别为QA＝1.8 cm3/s，QB＝1.4 cm3/s，此时2入口单位面积上的体积流率相等。假设入口处的流动为充分发展流，入口处的温度为473 K。

（2）共挤出流道区口模壁面

假设壁面无滑移，采用边界条件vn＝0，vs＝0，口模壁面的温度为473 K。

（3）共挤出自由表面

自由表面需要满足速度和应力边界条件，当不考虑表面张力时，vn＝0，fn＝0，fs＝0。

（4）自由端面

在无外力牵引的情况下，自由端面（图1中ABCDEF）上熔体的法向应力fn＝0，切向速度vs＝0。

（5）层间界面

忽略两熔体的表面张力，假设熔体间无相对滑移，界面上的速度场和应力场连续，vⅠs＝vⅡs，vn＝0，fⅠs＝fⅡs，Ⅰ、Ⅱ分别代表2种聚合物，界面上温度连续，热通量连续。

2 数值模拟结果及讨论

2.1 进料方案

本模型为双层共挤异型材，为了研究两聚合物不同组合对挤出胀大和变形的影响，本文列出了几种进料方案，如表2所示。方案Ⅲ和Ⅳ2入口材料相同，等同于单组分挤出。

表2 进料方案Tab.2 Feeding scheme

2.2 网格选择

在数值分析中，网格对计算结果的影响很大。一般来说，网格数量增加，计算精度会有所提高，但网格数量越多计算量越大、耗时越长且难收敛。因此，本文建立了3种网格，如图2所示。下面将选择一种合适的网格来进行本文的研究。计算3种网格方案Ⅰ的挤出胀大和变形情况，结果如表3所示，表中Δθ和ΔS的定义见图3。

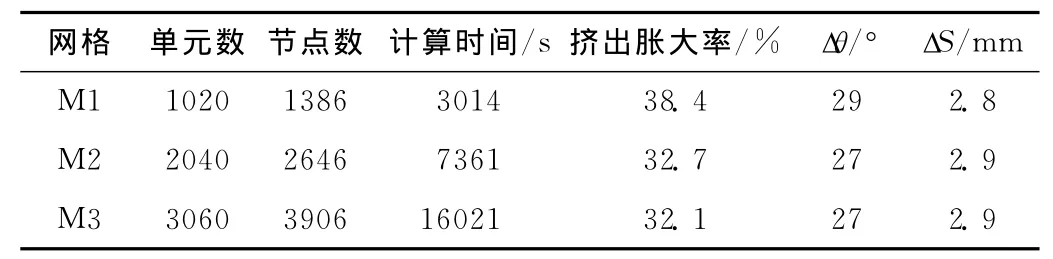
表3 各网格的基本信息和计算结果Tab.3 Basicinformation on the meshes and the computationresults

从计算结果可以看出，网格M2和M3的结果几乎相同，而网格M1的偏差比较大，综合考虑计算精度和耗时，本文选用网格M2。

2.3 共挤出胀大和变形分析

图3为各方案网格重置后的挤出胀大和变形图，其中各图左侧为共挤口模入口面（图1中MNPQRO）和共挤聚合物自由端面（图1中ABCDEF）沿Z轴视图方向上的截面对比。方案Ⅰ和Ⅱ的自由端面截面积分别为531 mm2和583 mm2，挤出胀大率分别为32.7%和45.8%。此处，应用角度Δθ来度量L形共挤自由端面两边夹角变化量，Δθ的计算公式为：

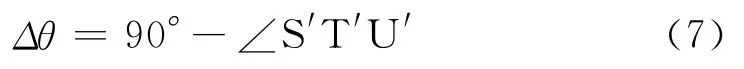
式中 ∠S′T′U′:网格重置后S′、T′、U′3点之间的夹角

根据公式（7）计算得到方案Ⅰ夹角变化量Δθ＝90°-63°＝27°，方案Ⅱ夹角变化量 Δθ＝90°-124°＝-34°。同时，通过测量点T和T′在XY平面上投影的距离ΔS来度量L形共挤异型材的偏转程度，方案Ⅰ偏转程度为2.9 mm，方案Ⅱ偏转程度为5.2 mm。

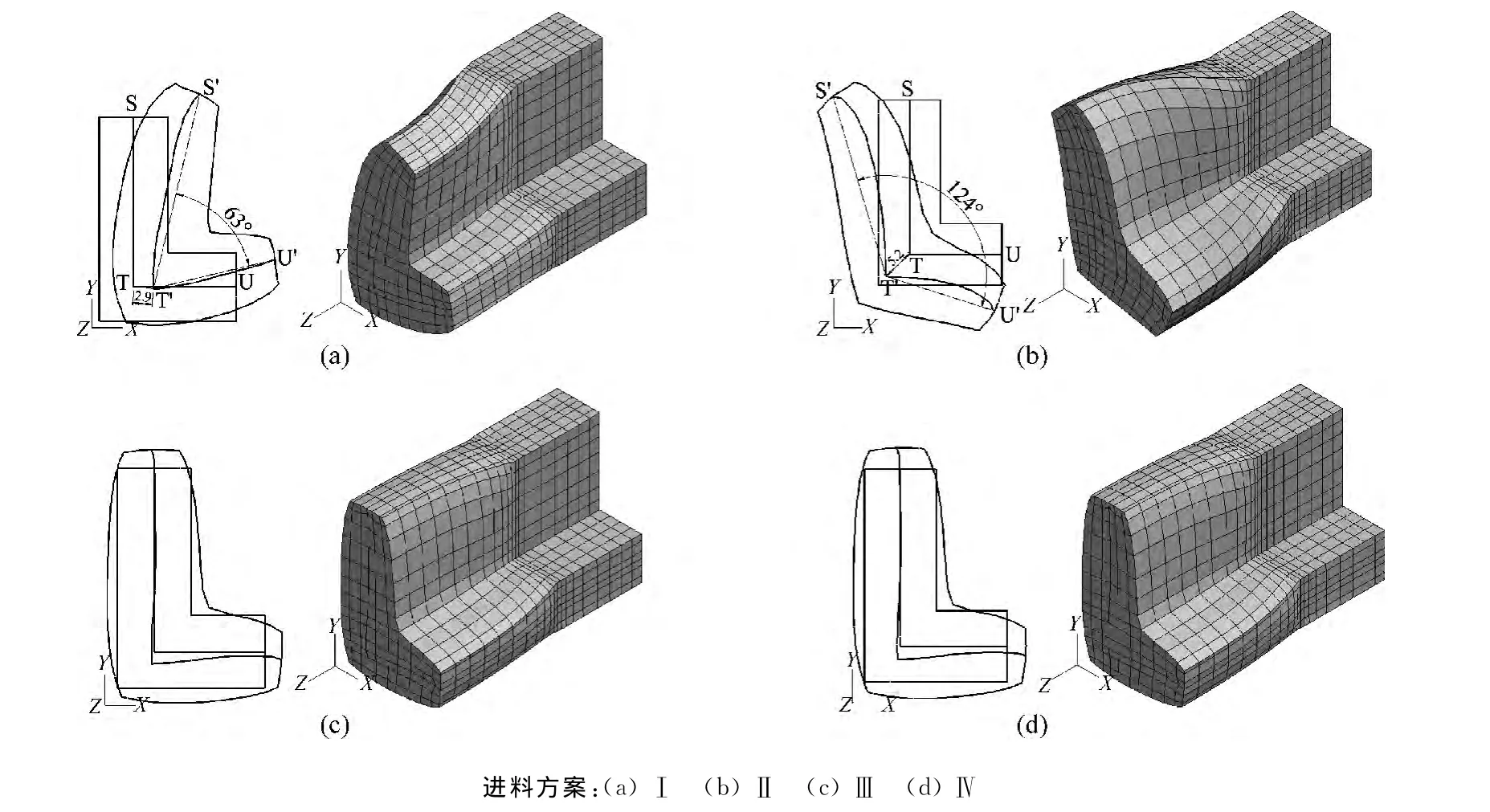
图3 网格重置后的变形图Fig.3 Gr id afterremeshing

以上研究表明，方案Ⅱ的挤出胀大和变形程度大于方案Ⅰ。对于方案Ⅲ和Ⅳ，由于2个入口的材料一致，等同于单组分挤出，然而不同于棒形和矩形等非异型材单组分挤出时只存在挤出胀大，L形异型材单组分挤出不仅存在挤出胀大，还存在离模偏转以及2边夹角增大的趋势；为了研究其中的机理，下面将研究口模出口面（图1中GHIJKL）的速度场以及剪切速率场分布。

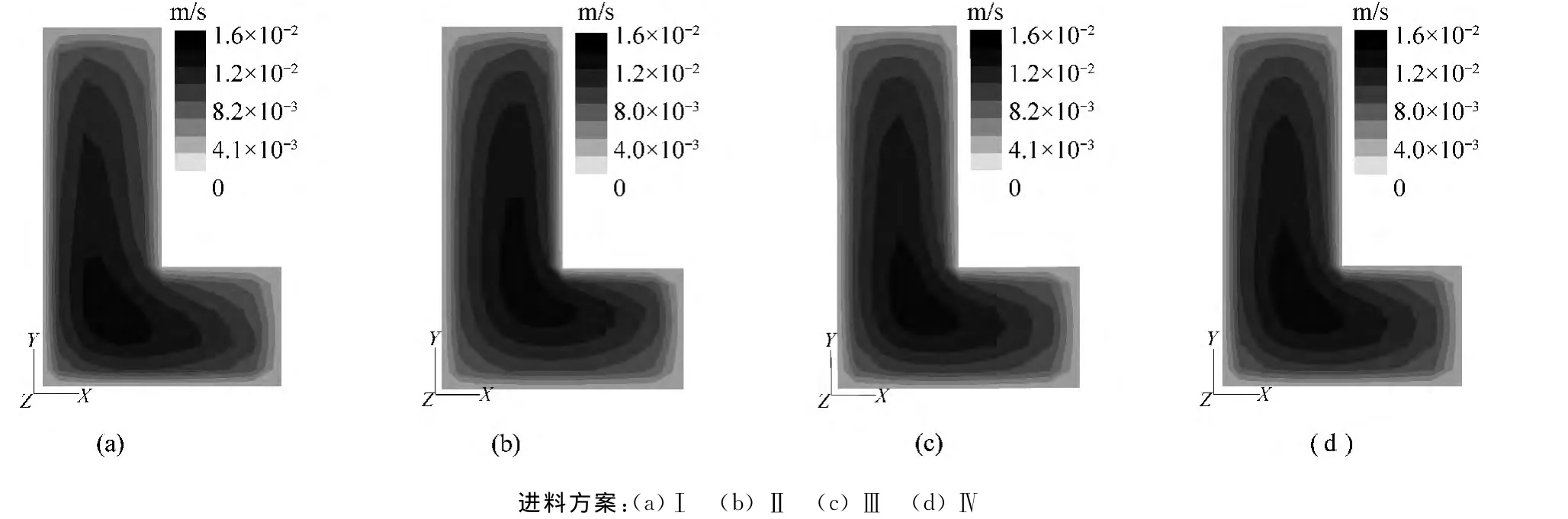
图4 口模出口面Z向速度分布图Fig.4 Distribution of Z velocity at die exit

图4为4种方案口模出口面的Z向速度分布，对比图4（a）和图4（b），可以发现2个方案均是具有低黏度的PP一侧Z向速度稍高于具有高黏度的PS一侧，这种速度的非对称分布导致了熔体离模后低黏度一侧向高黏度一侧偏转，如图3（a）和图3（b）所示；进料方案Ⅲ和Ⅳ中，2个入口的材料相同，即相当于单组分挤出，而观察图3（c）、（d）和图4，可以发现内侧的Z向速度稍高于外侧，熔体有向外侧偏转的趋势，这说明L形分层共挤的离模偏转不仅与2种材料性能差异有关，还与共挤口模的截面形状有关。笔者分析认为，L形口模截面内外2个侧边长不相等是造成此现象的主要原因，外侧边长更长，故所受壁面摩擦阻力更大，两侧所受摩擦阻力不平衡，也会导致熔体离模后偏转。

方案Ⅰ中，由于黏度的差异，低黏度的PP会向高黏度的PS偏转，即向内侧偏转，同时由于口模截面形状的影响，挤出熔体有往外侧偏转的趋势，然而黏度的差异造成的偏转克服了口模截面形状的影响，熔体仍然表现为向内侧偏转；方案Ⅱ中，黏度差异造成熔体往外侧偏转，而口模截面形状的影响也使熔体往外侧偏转，2种因素叠加，从而造成其偏转程度大于方案Ⅰ。

图5为不同方案下口模出口面的剪切速率分布云图，对比图5（a）、图5（b），可以看出方案Ⅱ的剪切速率稍大于方案Ⅰ，由于正应力效应[9]，方案Ⅱ的挤出胀大程度大于方案Ⅰ；综合4个剪切速率云图可以看出，内顶点处（内角＞180°）剪切速率较大；因此，在实际生产中应注意内顶点处的表面品质。

2.4 黏度比对共挤出胀大及变形的影响

为了研究黏度差异对L形分层共挤的影响，保持PP的黏度不变，将PS的黏度分别设定为2250、3750、4500 Pa·s，即黏度比分别为1.5、2.5和3，2种材料的其他参数保持不变，分析方案Ⅰ和Ⅱ的挤出胀大和变形情况。黏度比对挤出胀大和变形的影响如图6所示，从图中可以看出，方案Ⅱ的挤出胀大和变形程度均比方案Ⅰ大，且随着黏度比的增大，2种方案的挤出胀大和变形程度差异越大；同时，2种方案的挤出胀大和变形程度均随着黏度比的增加而增大，证明2种熔体黏度差异越大，挤出胀大和变形越严重。

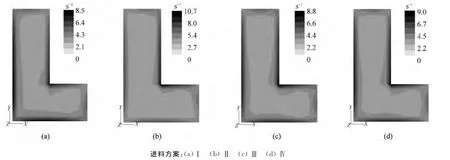
图5 口模出口面剪切速率分布图Fig.5 Distribution of shearrate at die exit

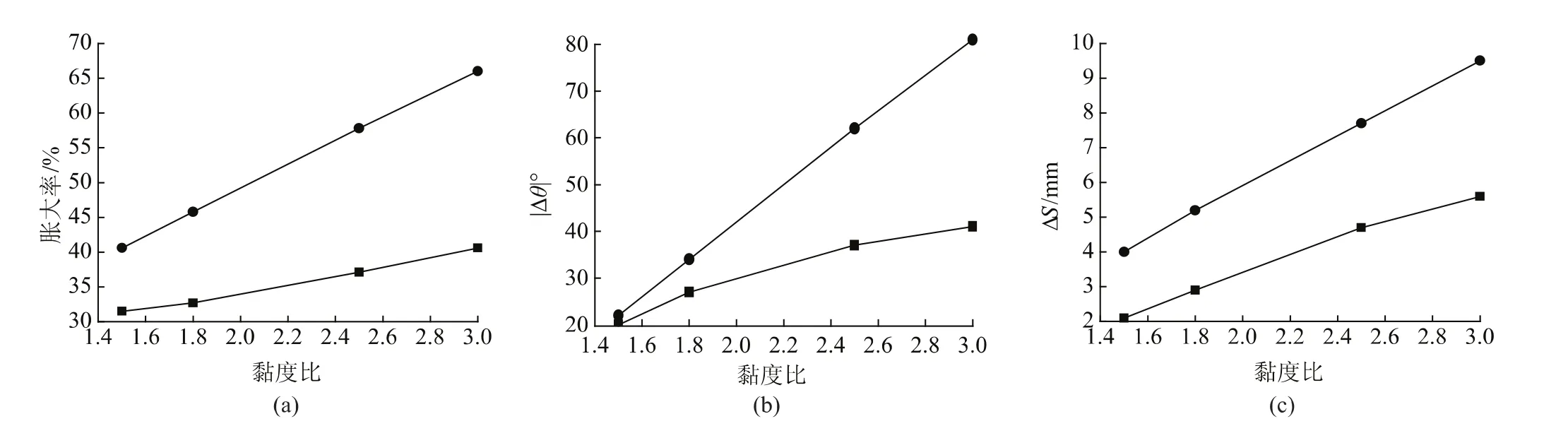
图6 黏度比对挤出胀大和变形的影响Fig.6 Effect of viscosityratio on die swell and deformation

2.5 误差分析

本文为了减少计算量，忽略了2种熔体汇料前的单独流动区域，同时，没有考虑熔体挤出后与外界的热交换，只考虑了熔体剪切流动时的黏性摩擦生热。实际共挤过程中，各熔体要经过各自的流道后再汇合，另外，熔体与外界温差较大，熔体离开口模后会遇冷收缩，这对异型材共挤的胀大和变形有一定的影响。文献[7]在对矩形分层共挤研究时，忽略了2种熔体汇料前的单独流动区域，并采用了等温假设，其数值模拟结果与实验结果基本吻合，说明本文所采用的假设虽会带来一定的误差，但对该型材的共挤出工艺仍有一定的参考价值。

3 结论

（1）在L形分层共挤过程中，共挤出胀大和变形不仅与2种熔体黏度的差异有关，还与L形共挤口模截面形状有关；熔体黏度的差异使2种熔体在口模出口面Z向速度呈非对称分布，低黏度熔体一侧Z向速度高于高黏度熔体一侧，从而导致低黏度聚合物向高黏度一侧偏转，且低黏度聚合物有包覆高黏度聚合物的趋势；

（2）由于L形异型材的非对称性，内外2侧熔体所受口模壁面的摩擦阻力不相等，即使单组分挤出时也会产生离模偏转，从而导致低黏度聚合物位于内侧时共挤出胀大和变形程度大于其位于外侧时；此外，随着2种熔体黏度比的增加，共挤出胀大和变形程度越严重，且低黏度聚合物位于内侧时与位于外侧时的共挤出胀大和变形程度的差异越大。

[1]贾明印，薛 平，朱复华，等.共挤出技术在聚合物成型加工中的应用及其设备的最新进展[J].工程塑料应用，2006，34（1）：66-69.Jia Mingyin，Xue Ping，Zhu Fuhua，et al.Application of Co-extrusion Technologyin Polymer Molding and Latest Development of Corresponding Equipment[J].Engineering Plastics Application，2006，34（1）：66-69.

[2]周宏志，江 波，许澍华.浅析高聚物共挤出技术[J].橡塑技术与装备，2004，30（9）：4-14.Zhou Hongzhi，Jiang Bo，Xu Shuhua.Simply Analyzed High Polymer Co-extrusion Technique[J].Chinarubber/Plastics Technology ＆ Equipment，2004，30（9）：4-14.

[3]Takase M，Kihara S，Funatsu K.Three-dimensional Viscoelastic Numerical Analysis of the Encapsulation Phenomenain Coextrusion[J].Rheol Acta，1998，37（6）：624-634.

[4]Anderson P D，Dooley J，Meijer H H.Viscoelastic Effectsin Multilayer Polymer Extrusion[J].Appliedrheology，2006，16（4）：198-205.

[5]黄益宾，柳和生，黄兴元，等.聚合物共挤成型界面位置的三维黏弹数值模拟[J].中国塑料，2008，22（9）：66-69.Huang Yibin，Liu Hesheng，Huang Xingyuan，et al.3D Viscoelastic Simulation of theinterfacein Coextrusion Process of Polymers[J].China Plastics，2008，22（9）：66-69.

[6]Keawkanoksilp C，Apimonsiri W，Patcharaphun S，et al.Rheological Properties and Melt Strength of LDPE During Coextrusion Process[J].Journal of Applied Polymer Science，2012，125（3）：2187-2195.

[7]黄益宾，柳和生，黄兴元，等.复合共挤成型中挤出胀大的三维粘弹数值模拟[J].高分子材料科学与工程，2010，26（3）：160-163.Huang Yibin，Liu Hesheng，Huang Xingyuan，et al.Three-dimensional Viscoelastic Simulation of the Die Swellin Coextrusion Process[J].Polymer Materials Science ＆Engineering，2010，26（3）：160-163.

[8]Phan-Thien N，Tannerri.A New Constitutive Equation Derived from Network Theory[J].Journal of Non-Newtonian Flu id Mechanics，1977，2（4）：353-365.

[9]徐佩弦.高聚物流变学及其应用[M].北京：化学工业出版社，2003：59-72.

[10]Wu T Q，Jiang B，Xu S H，et al.Three-dimensional Nonisothermal Simulation of a Coat Hanger Die[J].Journal of Applied Polymer Science，2006，101（5）：2911-2918.

[11]Ishikawa T，Kihara S，Funatsu K.3-D Numerical Simulations of Nonisothermal Flowin Co-rotating Twin Screw Extruders[J].Polymer Engineering and Science，2000，40（2）：357-364.