大型光伏电站方阵优化设计研究
2014-09-11周长友孙炜朱国锋
周长友,孙炜,朱国锋
(1.南京中核二三能源工程有限公司,南京 210008; 2.北京乾华科技发展有限公司,北京 100038)
1 问题的提出
近年来,随着国内外光伏市场的变化,国内对能源的需求日益加剧,与此同时,国内环境污染的问题也越来越严重。为了加强对环境污染的控制,我国积极发展清洁能源,对太阳能发电给予了大力支持,颁布了《太阳能发电发展“十二五”规划》并提出了指导方针和目标:到2015年年底,太阳能发电装机容量达到21 GW以上,年发电量达到 2.5 GW·h,我国光伏电站建设进入了快速发展的新阶段。
光伏方阵是光伏电站的重要组成部分,是光伏发电的基础与核心,光伏方阵的设计优劣直接影响着发电量和经济效益[1-2]。为规范光伏电站设计,住房和城乡建设部与国家质量监督检验检疫总局联合发布了GB 50797—2012《光伏发电站设计规范》,同年中国电力投资集团公司印发了《光伏发电工程典型设计》,其中的案例太阳山光伏并网电站一期工程设计具有典型设计的代表性。尽管光伏电站设计有了规范,但各地气候条件、地理位置、核心设备配置等均有差异,因此,有很多文献[3-6]研究针对某一案例或某一方面设计,提出了优化设计方法。基于上述思路,本文对我国西部大型光伏电站的建设经验进行了总结,在组串设计、组件倾角、阵列间距等方面提出了改进与优化方法。
2 光伏方阵设计
在通常情况下,大型光伏电站可根据场地统一模块化设计子方阵,子方阵容量为1 MW左右,布置形状为长宽相差不大的长方形,逆变器室位于方阵中间,配置2台500 kW逆变器和1台1 000 kV·A的升压变压器。在子方阵中,组件以最佳倾角安装,组串根据当地历史极限低温计算后取最大值或最大偶数值,阵列间距应满足当地冬至日09:00—15:00间光照度要求,其前后左右互不遮挡。在方阵典型设计的基础上,本文对以下几点技术进行研究。
2.1 最佳倾角与经济最优倾角
一般说来,光伏电站均以最佳倾角安装,组件斜面接收到的辐射量最大,即光伏方阵发电量最大化,在不考虑其他因素时,光伏组件斜面接收的辐射量最大,单位组件输出的电量最大,投资效益也应最大。然而研究结果表明,光伏组件斜面接收辐射量最大化与投资效益最大化并不一致。其原因是有的地方土地并非无偿使用,由于大型光伏电站占地面积巨大,根据不同纬度、阵列间距设计,1 MW光伏电站占地面积为2.0~2.6 hm2,几十兆瓦的光伏电站土地费用不可忽略。当土地面积一定且组件倾角不同时,组件表面辐射量、阵列间距、安装容量也不相同,组件倾角变化、辐射量变小、总发电量增加等多个因素之间存在一个平衡点,可通过技术经济分析来确定经济最优倾角,组件倾角从经济角度进行优化,有助于提高综合经济效益。
根据光伏电站的建设经验,以工程经济财务内部收益率、投资回收期等指标进行动态分析,光伏组件具有经济最优倾角。分析了新疆洛浦某20 MW光伏电站案例,在面积为46.9 hm2的场地上以不同的倾角以及组件间距安装不同容量的光伏组件,技术经济人员对发电量、征地费用、电价、贷款、土建及电气设备等建筑安装成本进行了相应的经济分析,分析结果见表1。通过表1可以看出,各方案财务指标均存在差异,在工程经济的几个重要指标分析中,倾角28°最具优势。由于倾角以5°为一个梯度,分析跨度较大,在不同角度时进行曲线分析,可以确定最优经济倾角在28°~30°之间,比辐射量最佳倾角低3°~5°,与参考文献[5]结论基本一一致。需要明确的是,经济最优倾角的确定与光伏电站容量、场地成本、纬度等多种因素相关,应根据具体项目具体分析。
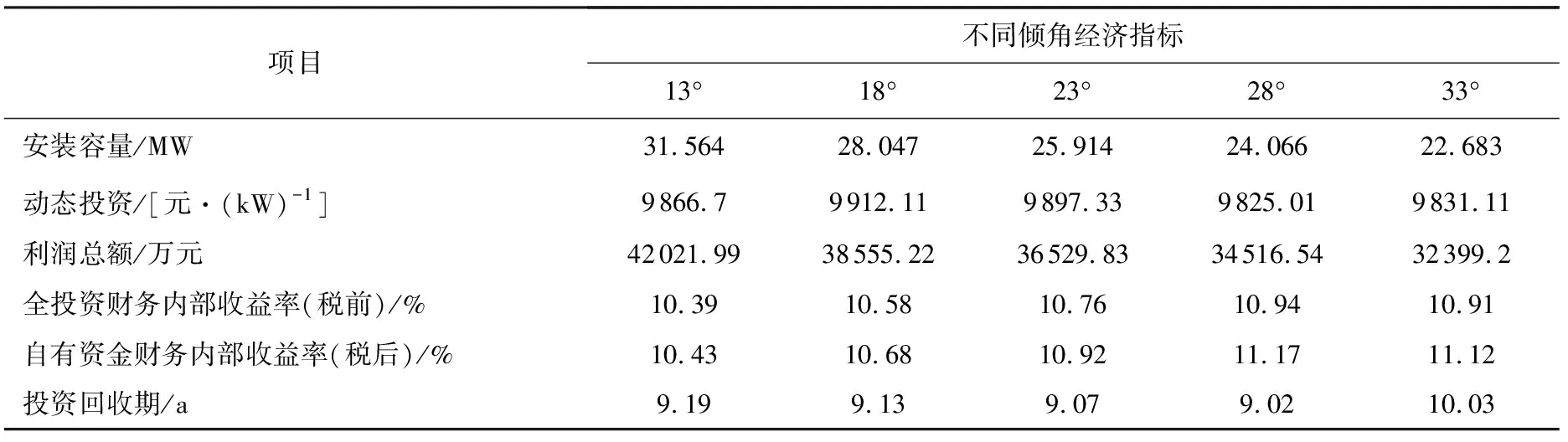
表1 新疆洛浦某项目不同倾角经济性分析
2.2 组串设计
在光伏方阵中,光伏组件串联后再并联,通过汇流箱输入逆变器作为一个发电单元。组串中各光伏组件的电性能宜保持一致,光伏组件的串联数应按下列公式计算
(1)
(2)
式中:Voc为标准测试条件下光伏组件开路电压;N为组串中串联的光伏组件块数;Vdcmax为逆变器直流端最大输入电压;Kv为光伏组件开路电压温度系数;Vmpptmin以及Vmpptmax为逆变器最大功率跟踪范围最小和最大电压;Vpm为光伏组件标准测试条件(STC)下工作电压;Kv′为光伏组件工作电压温度系数;t为光伏组件工作条件下的极限低温;t′为光伏组件工作条件下的极限高温。
为增大组串的输出电压,减少线路损耗,组件串联数量宜选用最大值,主要用公式(1)计算。在实际工程中,为方便支架设计及组件接线,组件串联数量往往会选择偶数值。影响组件串联数量的因素主要有:项目所在地近30年历史最低温度(t),逆变器最大直流输入电压(Vdcmax)、光伏组件的开路电压(Voc)以及开路电压温度系数(Kv)共4个参数,忽略了其他因素。实际上,Voc是辐照度的函数,计算中采用的Voc是光伏组件标准测试条件(空气质量为1.5,测试太阳电池的辐照度为1 000 W/m2,环境温度为25 ℃)下测试的参数,而当辐射量降低且其他条件不变时,Voc同时降低。从理论上来说,Voc值随辐射强度的增加呈对数方式增长[7-8]。当光伏电池处于开路状态时,对应光生电流产生的电动势就是开路电压。设I=0A(开路),Iph=Isc,则
(3)
(4)
式中:Iph为光生电流;Isc为参考温度光照下的短路电流;I0为二极管反向饱和电流;Kt为短路电流温度系数;TJ为光伏电池结温温度;Tr为参考热力学温度;G(t)为光照强度,W/m2;n为光伏电池的理想因子;k为玻尔兹曼常数,取值1.38×10-23J/K;q为电子电荷,取值为1.6×10-19C。
在可以忽略串联、并联电阻的影响时,Isc为与入射光强度成正比,在很弱的阳光下,Isc≤I0,因此
(5)
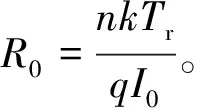
在很强的阳光下,Isc≥I0,
(6)
由此可见,在较弱阳光时,硅太阳电池的开路电压随光的强度做近似直线变化,而当阳光较强时,两者是对数关系;短路电流与辐射量呈线性关系,辐照度对晶体硅电池开路电压和短路电流的影响如图1所示。
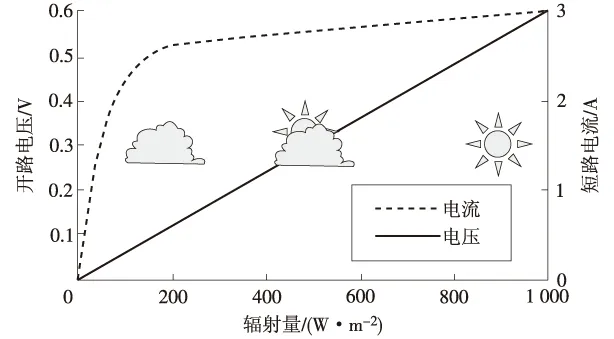
图1 辐照度对晶体硅电池开路电压和短路电流的影响[8]
温度是影响光伏组件开路电压的重要参数,当温度升高时,Voc线性减少,用公式表示为
Voc′=Voc[1+(t-25)Kv] ,
(7)
或者
Voc′=Voc+(t-25)kv。
(8)
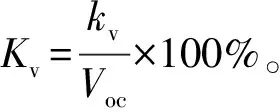
一般厂家提供的组件参数均为STC条件下的测试结果,理论上可通过光伏电池的数学物理模型以及厂家提供的组件参数模拟出不同辐照度和温度条件下的组件I-V曲线以及计算相关的特性参数[9]。PVsyst软件中也有类似功能,输入不同辐照度和温度的工况条件,可得出组件在该工况下的输出参数。厂家提供的光伏组件资料基本都含有组件在不同辐照度下的I-U曲线图,如图2所示。
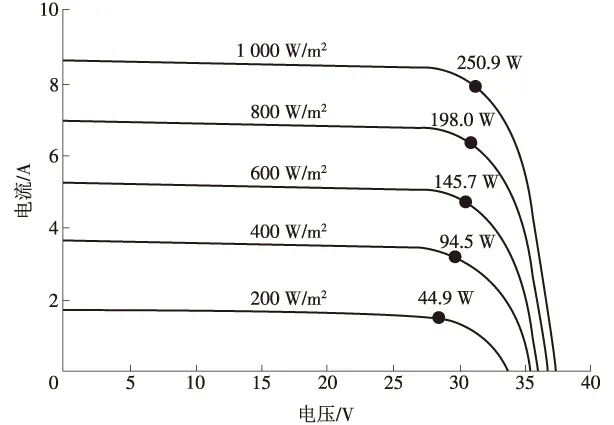
图2 晶硅组件在不同辐照强度下的I-U曲线
根据光伏组件的弱光测试曲线,光伏组件正常工作的辐射量范围为200~1 000 W/m2,当辐射量低于200 W/m2时,光伏组件的Voc急剧下降,同时由于逆变器有一个工作启动阈值,在较低的辐射量下不能启动工作。由于逆变器早上启动时是低辐照度低温,其他时间启动时辐照度和温度都已增大,此时光伏组件的结温会比环境温度高。因此考虑早上逆变器启动时,低辐照度下的现在市场主流的60片电池片(峰值功率为250 W档)光伏组件的Voc输出比STC测出的Voc参数小2~3 V(PVsyst软件中光伏组件数据库数据),此时光伏组串可串联的组件数量会增加。为了计算方便,同时符合工程实际情况,拟选用200 W/m2时的Voc参数计算。以尚德STP250S组件为例,在极限低温为-20 ℃应用时,查找数据得,标准条件下(STC)1 000 W/m2时Voc为37.3 V,200 W/m2时Voc为34 V,系统设计电压Vdcmax为1 000 V,组件开路电压温度系数-144 mV/℃, 尚德组件低温低辐射量时Voc计算见表2。
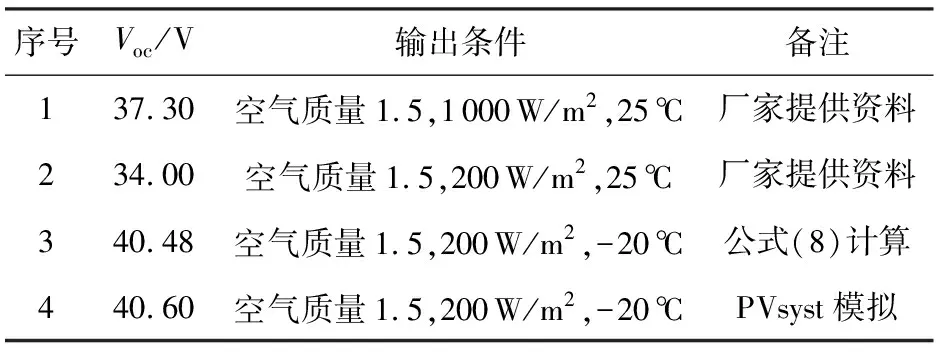
表2 尚德组件低温低辐射量时Voc
由表2可知,200 W/m2,25 ℃时的Voc和公式(8)计算得到的低辐照度低温时的Voc与软件模拟得到的Voc基本一致,误差仅有0.3%,计算方法比较可靠,进一步计算组串N,结果见表3。

表3 采用不同辐射量Voc计算组串N
当光伏组件工作时,组件的结温就会高于环境温度,且低辐照度时Vpm输出同样比STC测出的Vpm小,因此组串工作状态输出电压仍可满足逆变器最大功率点跟踪(MPPT)范围的电压上限。另外,光伏组件的衰减促使光伏组件Voc,Vpm减小,某型号光伏组件衰减测试见表4。考虑光伏组件的老化和功率衰减的因素,可以将组件串联数量优化。通过以上分析,光伏组串的组件数量可采用低辐照度200 W/m2,25 ℃时的Voc计算。
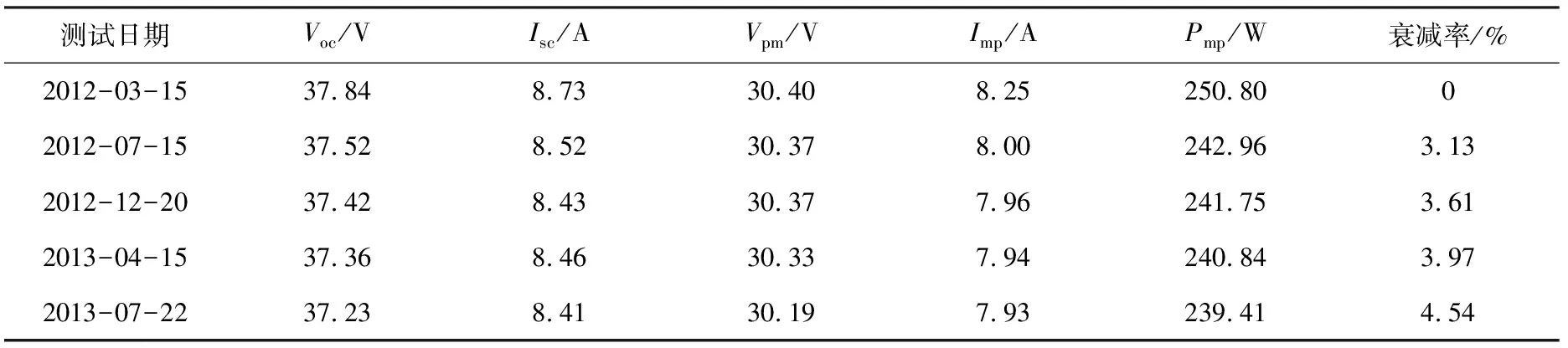
表4 某型号光伏组件衰减测试
当组串N=24时,在1 MW的光伏电站设计中,由于组串并联数量的减少,支架数量、汇流箱配置和直流电缆长度均会相应减少,因此,在大型电站中会凸显效益。
2.3 固定支架布置形式
由于固定支架比单、双跟踪支架投资少,维护简便,在大型光伏电站中应优先采用。固定支架一般根据光伏组件的规格型号、布置方式、光伏组串中组件数量并考虑安装场地特点进行结构设计。本文重点分析组串在支架单元上排布方式对支架、桩基电缆等的成本影响。
通常一个或多个组串布置在一个支架单元上,以某组串22块组件(长900 mm×宽165 mm)设计为例,组串布置方式有以下几种。
(1)竖向1排22块组件,单排串联为一个组串。支架、桩基与电缆用量比其他形式较多,不适用大型电站,常用于屋顶电站。
(2)竖向2排11块或2排22块组件,双排成串。竖向2排11块组件的布置在大型光伏电站中最为常用,双排成串U型串联接线方便,支架单元东西长11 m,当建设场地红线范围不规则时,应用比较灵活。将2个安装竖向2排11块组件的支架单元组合为一个支架单元,即为2排22块组件,支架单元东西长约22.2 m,在长度方面仍然便于安装和检修维护。例如宁夏中卫某20 MW光伏电站项目,以2排22块布置为主,2排11块为辅,在满足载荷要求的情况下,2排22块布置时支架基础采用2排7根桩基,2排11块时支架基础采用2排4根桩基,因此,对于44块组件来说,2排22块布置比2排11块布置桩基将减少1/8,支架东西间距的减少也带来方阵面积的减少和电缆用量的减少,节约了成本。在实际应用中,竖向2排22块组件比2排11块组件更为经济。
(3)横向双2排11或横向4排11,双排分别串联成串。此类型布置,经济性比竖向双排布置稍低,但横向四排支架略显庞大,施工操作不易,在电站中很少使用。
通过以上分析,以及山西大同某项目支架不同布置形式、桩基材质和直径相同经济性进行比较,比较结果见表5,可知支架单元上光伏组件竖向2排22块布置经济性较好。考虑到施工便利因素,竖向2排11块布置方式在场地起伏以及边界不规则时更有灵活性。如果电站地势起伏与边界不规则,建议采用2种支架统筹考虑。
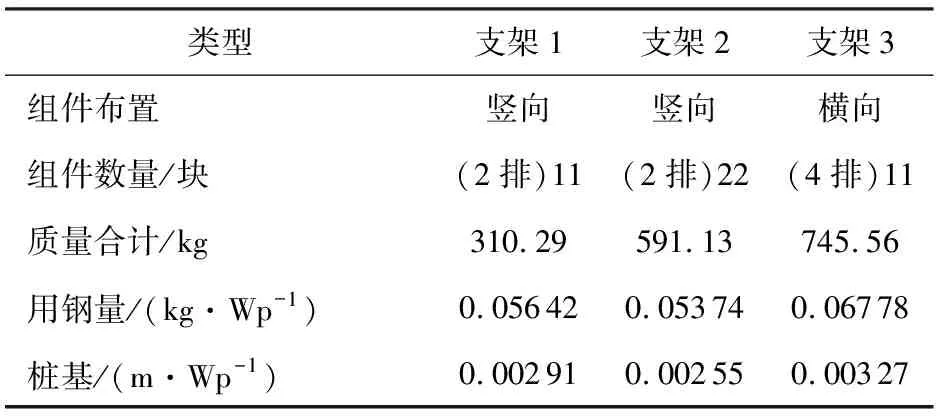
表5 支架与桩基经济性比较
2.4 阵列南北和东西向间距
光伏阵列的南北向间距以及东西向间距决定了光伏方阵的面积,直接影响土地成本和电缆成本。一般的设计原则是冬至日当地真太阳时09:00—15:00之间,光伏阵列前、后、左、右互不遮挡。GB 50797—2012《光伏发电站设计规范》中给出平整场地光伏阵列不被遮挡的阵列中心间距公式
(9)
式中:l为组件斜面长度;θ为组件倾角;ø为项目所在地纬度。光伏阵列间距示意图如图3所示。
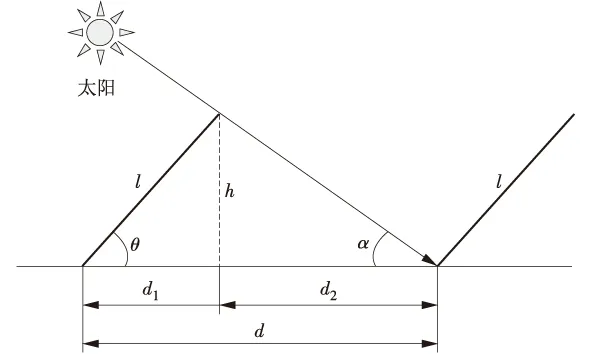
图3 光伏阵列间距示意图
由于大型电站因所占面积很大,自然场地基本都会存在地形起伏,且土石方平整既不经济也不环保。参考文献[4]推导了适合坡度场地的间距计算公式,优化了设计方法。
(10)
式中:DE-W为相邻东西阵列的中心距(阵列长度加相邻间距);iE-W为东西方向的坡度;iN-S为南北方向的坡度,定义北坡为正,南坡为负;日照间距系数R=cosβ/tanα,β和α分别为项目所在09:00时的太阳方位角和太阳高度角。光伏阵列的中心间距为阵列斜面投影d1与间距d2之和,d=d1+d2=d1+lcosθ+d2。
坡度场地的由于面积较大,起伏不定,坡度的分析选取可以兼顾道路竖向设计,采用子方阵分区域设计,比如“网格法”。网格法是用100 m×100 m或200 m×200 m等不同长宽的方形或矩形网格将场地分区,计算每一个小格四周的坡度,选取较大的坡度计算阵列间距,对于坡度不同的区域,光伏阵列的间距可适当取不同的间距值。本方法适用于坡度复杂场地,例如,中间高四周低的山坡场地和高低不平的滩涂场地。当场地没有东西向坡度时,即场地为正南坡或正北坡,分不同区域计算南北坡度,然后分区域间距设计。
据报道,最新建设的某些光伏电站阵列间距有进一步增大的趋势[10]。在阳光能源格尔木二期项目中,每排组件的间距从一期的5.7 m增加至6.0 m,以减少阴影的影响。华能格尔木三期也将10 MW子方阵间距从5.7 m增加至6.0 m,以对比不同间距下的发电量。有必要指出的是,阵列间距的增大会减少早上和傍晚时阵列遮挡时间,同时带来发电量增加与电缆量增加,与前面倾角经济优化减小间距减少占地面积相比,各有利弊,如何优化设计建议根据可利用面积以及目标装机容量等条件技术经济分析后选择。
光伏阵列的东西间距不同于南北间距,规范中没有规定间距大小以及计算方法。东西方向间距的大小同样影响光伏方阵的占地面积以及电缆长度用量,因此比较重要。在平整的场地上,东西向光伏阵列的组件安装高度一致,不会相互遮挡。对山地布置或地形坡度较大的场地,应考虑阵列中支架单元东西方向高度变化所引起的阴影遮挡,并在设计中采取针对性措施。当场地坡度较大时,应考虑东西相邻2个阵列的落差,除保证冬至日09:00东边阵列不遮挡西边阵列或15:00西边阵列不遮挡东边阵列外,还应进一步考虑夏至日相邻阵列是否遮挡,这是由于夏至日太阳辐照度在09:00之前与15:00之后仍然很高,应对这一部分辐射量提高利用率。例如,通过PVsyst模拟宁夏中卫市某光伏电站(37.3°N),光伏阵列西侧比东侧高0.5 m,东西间距0.5 m,虽满足冬至日15:00左右不遮挡时,但夏至日15:30左右就会出现左右遮挡而前后阵列没有形成遮挡。当东西间距为1 m时,夏至日出现左右遮挡的时间为16:30左右,如图4所示的东侧支架上西端刚出现阴影。因此,根据东西光伏阵列的高度差来考虑东西间距有实际意义,根据实际工程建设经验,在平整场地时,建议东西向间距为0.3~0.5 m,在预留作为检修通道用时,可设计为1 m,坡度场地相邻阵列存在高差时,东西向间距为相邻阵列的高差2倍以上为宜,在夏季可以减少早晚时间的遮挡以利用更多的光照。
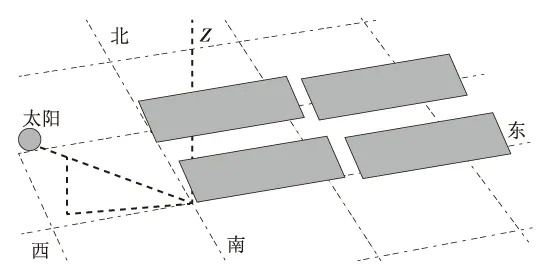
图4 PVsyst夏至日16:30阵列阴影模拟
3 结论
本文从安装倾角、组串数量、直流电缆接线等方面研究了大型光伏电站的方阵优化设计,根据研究结果,得出如下结论:
(1)大型光伏电站应根据安装容量和场地成本进行具体分析,选择经济最优倾角比选择组件倾斜面辐射量最佳倾角更有利于提高投资效益。
(2)提出了光伏组串设计采用低辐照度低温条件的计算方法,根据该计算方法可增加组串中组件数量,以减少电缆压降并减少电缆量。
(3)分析了组件在支架上的安装方式和支架选型,选用竖向2排22块组件布置方式在支架、桩基方面经济性较高。
(4)大型光伏电站建设场地面积巨大,有一定起伏,且本文提出采用“网格法”通过分区域计算阵列南北间距,并提出针对东西相邻阵列存在较大高差时,除满足冬季09:00—15:00之间不遮挡外,应兼顾夏季提高辐射量利用。
参考文献:
[1]Carrion J A,Estrella A E,Dols F A.The electrcity production capacity of photovoltaic power plants and the selection of solarenergy sites in andalusia(Spain)[J].Renweable Energy,2008,33(4):545-552.
[2]李文婷.荒漠并网光伏电站光伏阵列优化设计[J].青海科技,2010(1):25-27.
[3]肖景良,徐政.局部阴影条件下光伏阵列的优化设计[J].中国电机工程学报,2008,29(2):119-124.
[4]周长友,杨智勇,杨胜铭.北坡场地光伏发电站阵列间距设计[J].华电技术,2013,35(6):14-17.
[5]董霞威,庞春,苏国梁,等.光伏并网电站光伏组件安装倾角的选择设计[J].中国电力,2010,43(12):70-72.
[6]顾菊明.固定式光伏阵列组件排列方式的研究[J].华电技术,2012,34(S1):89-90.
[7]Wenham S R,Green M A,Watt M E,et al.Applied photovoltaics[M].Lodon:Earthscan,2007.
[8]崔容强,赵春江,吴达成.并网型太阳能光伏发电系统[M].北京:化学工业出版社,2007.
[9]邱纯,蔡涛.任意辐射强度与温度下硅光伏电池模型参数的计算方法[J].太阳能学报,2013,34(9):1626-1632.
