商业折扣下批量订购优化模型的修订与应用
2014-09-10胡平
胡 平
(淮阴工学院 数理学院 江苏 淮安 223003)
0 引言
商家为了促销某种产品,一般采用商业折扣的优惠政策,购价为每次订货量Q的分段函数K(Q):
(1)
其中,k1>k2>…>kn,0 购货企业为了得到商家的折扣优惠价格,必须加大购货量,从而增加了购货企业的商品储存成本。购货企业每次购货量为多少,才能使购货总成本最低?目前,解决这类问题的方法是比较选择法[1-3]:分别计算购货量为Q∈[ai-1,ai)时单位时间内购货总成本fi,从{fi}中选择最小的fmin,fmin所对应的Q就为最佳的订货量Q*。 这种比较选择方法计算麻烦,所以我们对这种商业折扣下的订购模型进行修订,引用0-1变量,构建了带有约束条件的非线性规划模型,由模型可直接解得最佳订货量Q*,并给出范例,以帮助大家理解与使用这种决策模型。 假设商家能够及时供货,有商业折扣;购货企业在单位时间内某种产品的需求量R为已知常数;该产品单位储存成本以及缺货成本,为已知常数(分别为C1、C2),或与货价(成本)K(Q)有关;每次订货成本C3为已知常数;我们要建立一个综合的数学模型,以确定购货企业的最佳订货量Q*,或最大缺货量S。 单位时间内购货总成本f(Q)为: f(Q)=储存成本+缺货成本+订货成本+购货费 (2) 如果单位时间内每件货物存储费为价格的u%,则单位时间内每件存储费为u%×K(Q)。一般地,可设单位时间内每件存储费为: C1=(1-α)c1+α×u%×K(Q) 其中,存储费与货价无关时α=0,存储费与货价有关时α=1。 (3) 如果单位时间内每件缺货费为价格的v%,则单位时间内每件缺货费为v%×K(Q),所以,单位时间内每件缺货费C2=(1-β)c2+β×v%×K(Q),其中,缺货费与货价无关时β=0,缺货费与货价有关时β=1。 (4) (5) 若单位时间内货物的需求量为R,则 单位时间内购货费=R×K(Q) (6) 将式(3)、(4)、(5)和(6)代入式(2)得到: 由于K(Q)为分段函数,对f(Q)求极值较困难,所以我们引入0-1变量: 则式(1)可以表示为: K(Q)=k1y1+k2y2+…+knyn (7) 其中,满足以下约束条件: (8) M为比an-1充分大的常数。 在式(8)中,假如y2=1,由第1等式可得y1=y3=…=yn=0,由第2不等式Q-a1<(1-y1)M,得Q-a1 综上所述,我们得到了购货企业确定订货量Q的优化模型,见模型1。 模型1: 当S=0,α=0时,模型1属于不准缺货,C1为常量的情形1; 当S=0,α=1时,模型1属于不准缺货,C1与货价有关的情形2; 当S>0,α=0,β=0时,模型1属于允许缺货,C1、C2与货价无关情形3; 当S>0,α=1,β=0时,模型1属于允许缺货,C1与货价有关、C2与货价无关情形4; 当S>0,α=0,β=1时,模型1属于允许缺货,C1与货价无关、C2与货价有关情形5; 当S>0,α=1,β=1时,模型1属于允许缺货,C1、C2与货价都有关情形6。 例1:某公司全年需用某种配件1200 件,每次订货成本 400 元,每件年存储成本 6 元,每件配件10元,如果订货批量在 600 件以上(含600件),则有2%的价格折扣,那么该公司的最佳经济批量是多少? 依题意知此问题属于情形1。 依模型1,得到具体的规划模型2: 利用LINGO软件编程解得:按价格K=9.8元批量进货600 件,全年进货总成本为14360 元。此结果与文献[1]的结论一致。 例2:某公司全年需用一批外购件 8000 件,每次订货成本100元,每件年存储成本率25% ,订购时如果一次购进量不小于850 件时,单价8元;如果一次购进量小于850 件时,单价10元,那么该公司的最佳订购批量是多少? 依题意知此问题属于情形2。 构建规划模型3: 利用LINGO软件编程解得:按价格K=8元批量进货894.4272件,全年进货总费用为65788.85 元。此结果与文献[1]的结论一致。 例3:某公司全年需用一批外购件300件用于维修设备,每次订货成本200元,每件年存储成本率20% ,如果一次购进量小于50件时,单价为500元;如果一次购进量小于100件时,打九六折,单价为480元;如果一次购进量达到或超过100件时,打九五折,单价为475元。每件年缺货成本率为60% ,那么该公司的最佳订购批量和最大缺货量是多少? 依题意知此问题属于情形6。 构建规划模型4: 利用LINGO软件编程解得:按价格K =475元批量进货100件,最大缺货量25件,全年进货总费用为146662.5 元。 如果不允许缺货,例3就为文献[2]中的例题,在模型4中,增加条件,利用LINGO软件编程解得:按价格K =480元批量进货50件,全年进货总费用为147600 元。此结果与文献[2]的结论一致。 针对商业折扣条件下的存储问题,我们引入0-1变量,建立了的批量订购优化模型,该模型适用于多种情形下,具有一定的通用性。由实例说明了我们建立的非线性规划模型,不但便于理解与构建,而且求解方便。如将此购货模型融入到运筹学教材中,将起到承上的作用,使学生更易理解与掌握。此规划模型可为企业经营管理者提供购货决策借鉴。 参考文献: [1] 谭丽娜.不同折扣条件下存货经济批量研究[J].商业时代,2012(32): 20-21. [2] 韩伯棠.管理运筹学[M].北京:高等教育出版社,2008. [3] 田世海.管理运筹学[M].北京:科学出版社,2011.1 模型的修订
1.1 问题的描述
1.2 模型的修订
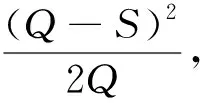
2 实例
3 结论
