判断点与多边形拓扑关系的改进算法
2014-09-10夏幼明
向 俊,王 静,夏幼明
(1.广西广播电视大学 教学资源与技术中心,广西 南宁530022;2.中国电信集团山东分公司网络中心,山东 济南250101;3.云南师范大学 信息学院,云南 昆明650092)
0 引 言
在矢量GIS空间拓扑关系研究中,点与多边形位置关系的判断是最基本的问题,也是比较复杂的问题。许多学者研究了诸多算法来解决点与多边形位置关系问题。如射线法、转角法及改进的射线法[1],射线法能较好地解决点与复杂多边形的位置关系。Sheng Yang等人针对点与多边形位置关系判断问题,提出了一种数值稳定的解决方法,该方法准确性较高,但时间代价大[2]。Juan J为了减少判断点与多边形关系时计算所耗费的时间,提出了一种新的基于分层的数据结构分析方法,该方法能减少算法的复杂性[3]。该方法优点是判断准确,缺点是运行时需要特定的平台支持。刘梁为解决以往算法的不可靠和过于复杂问题,提出了面积判断法,解决了在含有孤岛的多边形中,点与多边形的关系判断问题[4],该方法具有准确性、灵活性等优点,但该方法未应用于复杂的多边形中。Jing Li等人为了提高判断点是否在多边形中的效率,提出通过在凸多边形集中分解成单个多边形,然后构建BSP树,在多边形中,算法通过两步执行一个包含查询,该方法的执行效率较高[5]。李楠等为了解决多边形内外算法中BSP树退化为链表的问题,提出一种改进的点在多边形内外的判断算法。首先对水平扫描线按照Y值进行排序,然后将水平扫描线按二分法的顺序插入到BSP树中[6],实验结果表明该方法具有最优的查找效果,算法简单易实现,是正确有效的。刘亚彬等通过计算交点数的奇偶性,给出判断点与多边形拓扑关系的方法,该方法能准确判断简单多边形,但不能有效的应用在复杂多边形中[7]。陈树强等将矢量与射线相结合来判断点与多边形的关系,该方法简单、快速,但对复杂多边形准确性不高[8]。Luo Guo等人提出了4个指标将点与多边形关系应用在土地利用中,但这些指标有局限性,且效率不高[9]。董秀山为提高判断点与多边形位置关系时的速度,提出首先查找所有顶点在确定区域内斜率最小点,以此作射线,该射线不穿过多边形顶点的新算法,该算法效率高,但不适合多边形顶点数少的情况[10]。综上所述,较多学者从不同的角度和原理提出不同的判断点是否在多边形中的算法,部分学者则是在判断点与多边形关系现有算法的基础上,通过改进和扩展提高算法准确性和效率,但还不能很好解决判断点与复杂多边形关系。本文根据射线所经过不同类型的顶点,提出加1加2和加3运算改进并扩展了射线法,该算法的原理简单,判断准确性高,不仅在简单多边形中有效,而且在不同类型的复杂多边形中也有效。
1 基本概念
多边形:是系列首尾相连接线段的有限集合。设多边形为P,可以用点序列P0,P1,…,Pn-1,Pn=P0表示,P0P1,P1P2,…,Pn-1Pn=Pn-1P0是多边形的边,Pi(i=0,1,…,n-1)是多边形的顶点[11]。
2 射线算法基本原理
2.1 射线算法基本思想
一条射线以点P为起始点,然后延长,穿过多边形的边界次数称为交点数目。如果交点数目是偶数时,则点P在多边形外部;如果交点数目是奇数时,则点P在多边形内部[12]。在图1中,如点in1和点out1所示。
2.2 射线算法优缺点分析
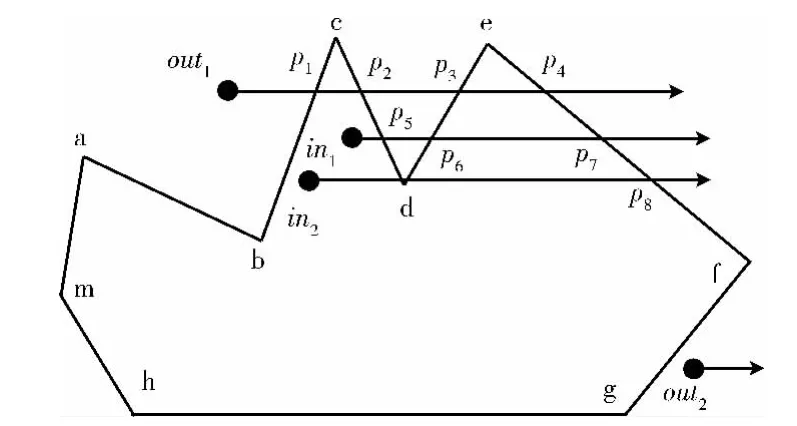
图1 简单多边形
在图1中,以out1点为起点的射线延长到多边形时经过P1,P2,P3,P4这4个交点,以out2点为起点的射线与多边形交点个数是0,以in1点为起点的射线与多边形交点是3;根据射线法判断out1点和out2点在多边形的外部,in1点在多边形的内部;该算法原理简单,思想明确,效率比较高,但存在不足:如以in2点为起点的射线与多边形交点是2,则判断该点位于多边形外,与实际相矛盾。对于以下特殊的情况:①不能处理公共顶点,即射线与多边形两条边的交点重合且两条边位于射线的同侧;②不能处理带空洞的多边形,即射线穿过带洞的多边形;③不能处理过共四边或共2n(n>2)边的交点,即射线与多边形四条以上的边相交而且交点重合;④不能处理重叠的多边形,即射线穿过在多边形内部重叠的另一个多边形。以上4种情况如果使用射线法则会得到错误的结果,因此该方法存在着缺点。
3 射线算法的扩展和改进
3.1 判断射线是否与边界有交点的方法
方法1:如果边界的两个端点分别位于射线的上下两侧,也同时位于判断点的右侧,则射线与该边界有交点[13]。在图1中,out1点与边界bc;设判断点为P0(x0,y0),边 界 的 两 个 端 点 为 Pi(xi,yi)、Pi+1(xi+1,yi+1);(xi>x0∧xi+1>x0)and ((yi>y0∧yi+1<y0)or (yi+1>y0∧yi<y0))。
方法2:如果边界的两个端点分别位于射线的上下两侧,并分别位于判断点的左右两侧,则射线与边界点可能有交点也可能没有交点。在图1中如in1点与边界bc和cd的关系。如果判断点与边界点的下侧端点连线的斜率小于该边界的斜率,即边在判断点的左侧,则无交点[13]。如果判断点与边界点的下侧端点连线的斜率大于该边界的斜率,即边在判断点的右侧,则有交点[13]。
方法3:在最小边界矩形方法基础上,本文提出通过比较面积大小,来判断射线与多边形边界是否相交。如图2所示。
在图2(a)中,设多边形任意两个端点为Pi和Pi+1,由端点Pi和Pi+1作最小边界矩形 (APiBPi+1),以P0为起始点的射线与边界线相交于点C,与最小边界矩形的边相交于点I。在图2(b)中,由端点P’i和P’i+1作最小边界矩形A’P’iB’P’i+1,以P’0为起始点的射线与最小边界矩形的边相交与点I’。
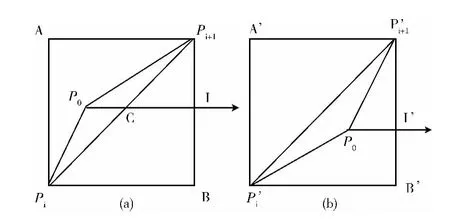
图2 射线与多边形边界关系
在图2(a)中,多边形P0IPi+1的面积为S1,多边形P0IBPi的面积S2,最小边界矩形APiBPi+1的面积为S。如果S/2< (S1+S2),则射线与多边形边界有交点。如果S/2= (S1+S2),则射线起始点在多边形边界上 (在图2(a)中,如C为射线的起始点的情况)。如果S/2> (S1+S2),则射线与多边形边界无交点,如图2(b)所示:S(A’P’iB’P’i+1)/2>S(P’i+1P’0I’)+S(P’0I’B’P’i)。
3.2 判断射线经过的顶点类型的方法
设由端点 Pi-1(xi-1,yi-1),Pi(xi,yi),Pi+1(xi+1,yi+1)3个点构成多边形Pi-1PiPi+1的三条边界线,其中该多边形的两条边界线分别是Pi-1Pi和PiPi+1,Pi称为多边形的顶点或者两条边的交点。设P0(x0,y0)是判断点。有如下4种类型:
类型1:向量 (Pi+1-Pi)× (Pi-Pi-1)≠0,并且经过顶点Pi的两条边界线Pi-1Pi和PiPi+1位于射线的同侧。判断条件y0=yiand((yi-1>y0∧yi+1>y0)or(yi-1<y0∧yi+1<y0))。
类型2:向量 (Pi+1-Pi)× (Pi-Pi-1)≠0,并且经过顶点Pi的两条边界线Pi-1Pi和PiPi+1位于射线的不同侧。判断条件y0=yiand((yi-1>y0∧yi+1<y0)or(yi-1<y0∧yi+1>y0))。
类型3:图4中E,F,G,H,J为5个点,其中E,G,H,J为顶点。当向量 (E-F)× (F-H)=0并且(G-F)× (F-J)=0时,此时F是线段EH和JG的交点,而不是多边形的顶点。
类型4:图4中当C和F是多边形KCDEFJ的顶点时,并且射线L’2经过的顶点与其余的顶点组成多多边形。如:ABC、KCDEFJ、GFH等多边形。设顶点的坐标分别为 (A(xA,yA),B(xB,yB),C(xC,yC),D(xD,yD),E(xE,yE),F(xF,yF),G(xG,yG),H(xH,yH),J(xJ,yJ),K(xK,yK)),起始点 X1(x1,y1),X2(x2,y2)如下2种判断条件:
条件1:当多边形的两条边在射线的同一侧。判断条件:y1=yCand (yA>yC)∧ (yB>yC)∧ (yK<yC)∧(yD<yC)。
条件2:当多边形的两条边界在射线的不同侧。判断条件:y2=yFand (yE>yF)∧ (yJ<yF)∧ (yG>yF)∧(yH<yF)。
算法描述:首先要计算点是否在多边形的任何一条边界上,如果点不在边界上时,则以该点为起点,沿平行于x轴的方向作射线l,并且l与多边形边界相交,射线方程表示为其中u>>0。
假设u>>0,存在如下4种情况:
情况1:当射线不与多边形边界重合并且经过多边形的某个顶点 (射线经过多边形两条边界的交点):如果连接该顶点的两条边在射线的同一侧 (如图3的L2过点d),则交点数加1;如果连接该顶点的两条边不在射线的同一侧 (如图3中L2过点f),则交点数加2。
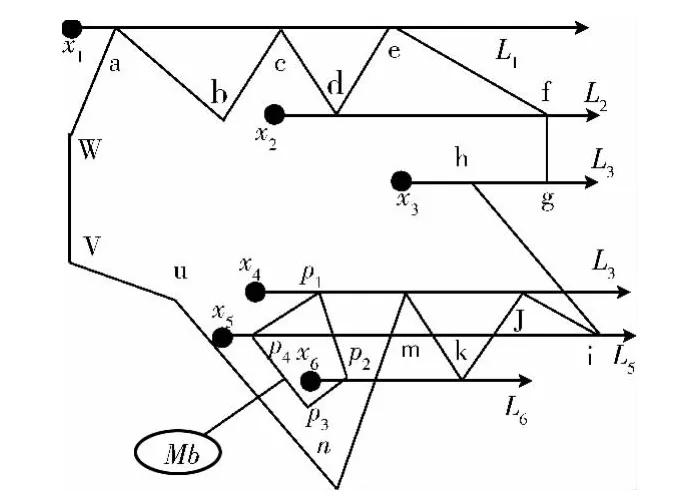
图3 复杂多边形
情况2:如果射线与多边形的某条边重合,如图3所示,射线L3经过边界线段hq,则将重合线看作一个交点I,然后确定与重合线段两个端点 (h,q)相连的线段与射线的位置关系,由情况1的方法计算交点数。
情况3:在多边形中,如果连接该顶点共有四条边,当任意能组成多边形的两条边分别位于射线的同一侧时如:AC和BC,KC和DC (如图4中L’1过点C),则交点数加1。当任意能组成多边形的两条边分别位于射线的不同侧时如:EF和JF,GF和HF (如图4中L’2过点F),则交点数加3。
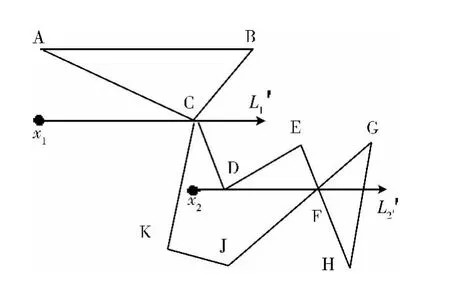
图4 多多边形
情况4:在多边形中,当连接该顶点共有2n(n>2)条边,并组成多个多边形时 (如图5中由V7V8V9、V1V2V9、V5V6V9和V3V4V9这4个三角形组成),此时只需考虑过该顶点的射线所穿过的部分多边形 (如图5所示,L1穿过V7V8V9和V3V4V9两个三角形,从而简化为上面的情况3;当射线只过顶点,不穿过部分多边形时 (如L1过三角形V1V2V9和V5V6V9的公共点V9),则交点数加1。且该算法适用于带有空洞的复杂多边形 (如图3多边形Mb)。
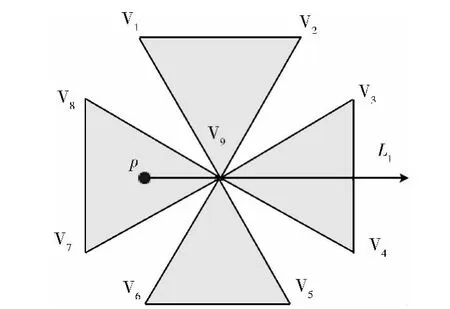
图5 复杂多多边形
本文判断算法的计算模型:设Ci表示初始的交点数目;Ii表示射线与多边形边界的交点;TVs表示位于射线同侧的两条边的交点组成的顶点类型,Vs表示同侧的顶点数目;TVd=2表示位于射线不同侧的两条边的交点组成的顶点类型,Vd1表示不同侧的顶点数目;TVd≥4表示多边形中至少四条边的交点组成的顶点类型,Vd2表示该类型顶点的数目。V∞表示将射线与边重合部分看成的一个顶点,TV∞表示该顶点的类型。射线与边有重合,则初始化时重合部分的交点数为∞。其中Ci=Ii+Vs+Vd1+Vd2,Vs = NUM(TVs),Vd1=NUM(TVd=2),Vd1=NUM(TVd≥4),Ni=Ci+∞ ,Ni,Ci,Ii,Vs,Vd1,Vd2∈ (1,2,...,n),V∞ =1。NUM()是计算该类顶点数的函数
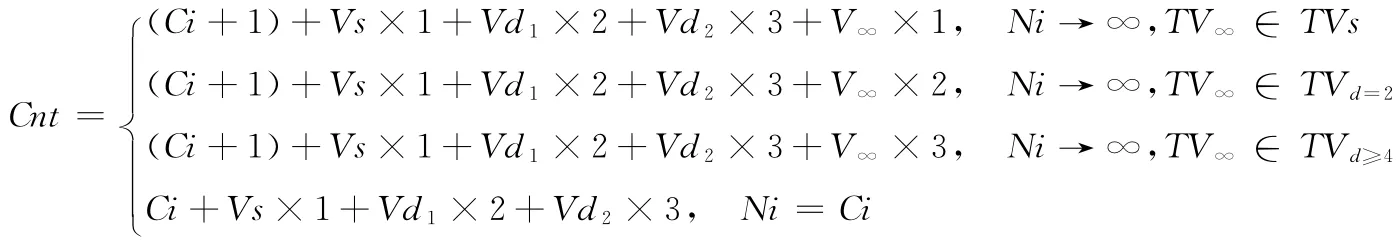
3.3 判断点与多边形的位置关系算法 (JP-ALA)
考虑的文章的篇幅,本文给出了算法的伪代码:
输入:组成多边形S的闭曲线L<p1,p2,…,pn,p1>,目标点P0(x0,y0)。
输出:点P0在多边形内部,点P0在多边形边界,点P0在多边形外部。
算法实现步骤:
步骤1 初始化以P0为起始点作一条射线l延长至无穷远。
步骤2 if射线l与多边形的某一条边pipi+1不重合then计算射线l与多边形所有边的交点个数为N。并标记所有交点 TVi(i=1,2,…,n)的类型 TVi∈ {TVs,TVd=2,TVd>=4}。
步骤3 if射线l与多边形的边界pipi+1重合then计算射线l与多边形所有未重合边界的交点个数为N,将重合的线段看成一个点,N=N+1,并且标识该点TVi的类型。
步骤4 if P0在多边形的边界上then P0在边界上;算法结束。
步骤5 if射线没有经过多边形的某个顶点then A1()else M=N,执行循环体。
Do
循环次数从1开始累加
步骤6 if射线经过的点是多边形相邻两条边的一个交点 (或多边形顶点)时then
if连接该顶点的两条边在射线的同一侧then N=N+1;
if连接该顶点的两条边分别在射线的不同侧thenN=N+2;
步骤7 if射线经过的某一点是由2n(n=2)条多边形边界相交后的一个交点时then
if能组成多边形的任意两条边分别位于射线的同一侧时then N=N+1;
if能组成不同多边形的任意两条边分别位于射线的两侧时then N=N+3;
步骤8 if射线经过的某一点是由2n(n>2)条多边形边界相交后的一个交点时then
if射线只过顶点不穿过多边形的某一部分then N=N+1;
if射线穿过多边形的某部分then保留射线穿过的部分多边形 (如图5所示三角形V7V8V9和三角形V3V4V9),根据穿过的多边形重新标记该交点的类型,执行步骤9;
步骤9 根据不同点类型,当标记为单顶点goto步骤6,标记为多条边相交的顶点,if n=2 thengoto步骤7 else goto步骤8;
While循环次数<=M
步骤10 当循环次数大于M时,退出循环,调用函数A1()。

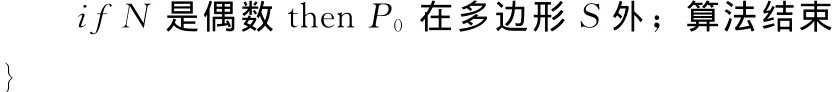
4 4种不同判定算法执行结果对比分析
在图3中,本文算法分别与文献 [12]算法、文献[13]算法和文献 [7]的算法对比分析见表1。
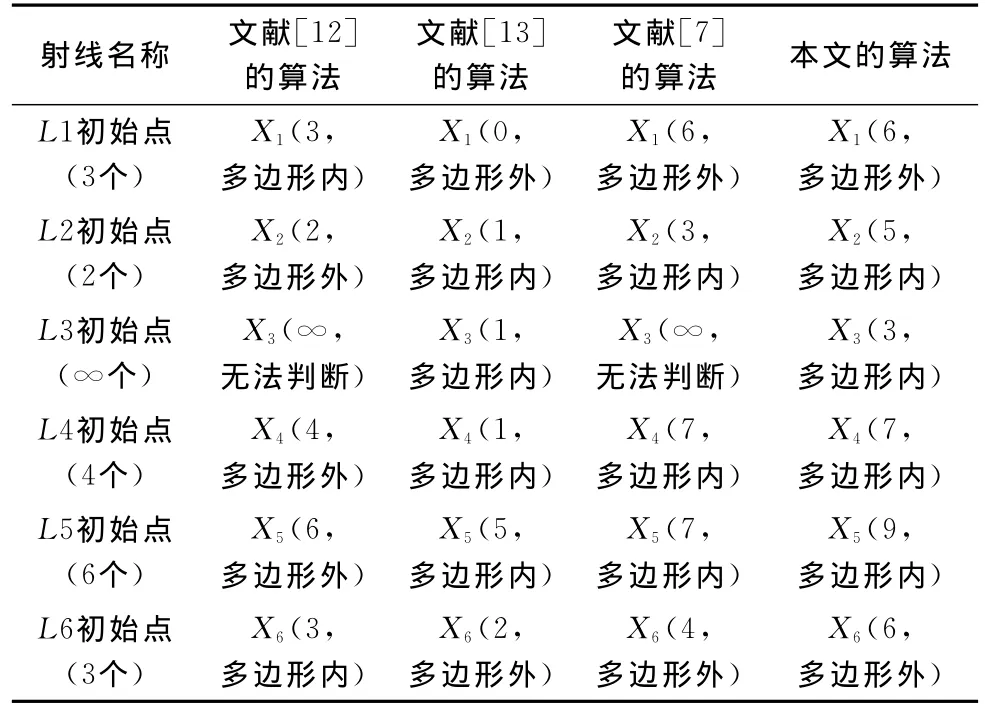
表1 针对图3的4种算法的对比分析结果
(1)L1经过3个顶点a,c,e初始交点数Ci=3,并且分别连接这3个顶点的两条边都是位于射线L1的同一侧。文献 [12]的算法交点数为3,判断X1在多边形的内部,与实际情况不符;文献 [13]和文献 [7]的算法交点数为偶数,则X1在多边形的外部;本文的算法,计算交点数Cnt=Ci+3*1=6,则X1在多边形的外部,与实际情况相符。
(2)L2与多边形的有两个初始交点d,f,Ci=2,其中连接顶点d的两条边位于射线同侧,连接f的两条边位于射线的两侧。文献 [12]的算法交点数为2,则X2在多边形的外部,与实际情况不符;文献 [13]和文献 [7]的算法判断X2在多边形的内部;本文的算法,计算交点数Cnt=Ci+1*1+1*2=5,判断X2在内部,与实际相符。
(3)L3与多边形的边重合,文献 [12]和文献 [7]的算法无法判断。文献 [13]算法和本文算法先简化为一个交点,本文算法先根据计算模型,判断X3在多边形内部,与实际相符。
(4)L4与多边形的初始交点数Ci=4,有3个顶点位于射线的同一侧。文献 [12]的算法判断X4在多边形的外部,与实际不符;文献 [13]的算法和文献 [7]的算法判断X4在多边形内部,本文的算法计算交点数Cnt=Ci+3*1=7,则X4在多边形的内部,与实际相符。
(5)L5初始交点数为6,文献 [1]算法判断X5在多边形的外部,与实际不符;文献 [12]的算法和文献 [7]算法判断X5在多边形的内部;本文的算法计算交点数Cnt=Ci+1*1+1*2=9,判断X5在多边形内部,与实际相符。
(6)L6初始交点数为3,文献 [12]算法判断X6在多边形的内部,与实际不符;文献 [13]算法和文献 [7]算法判断X6在多边形的外部;本文的算法计算交点数Cnt=Ci+1*1+1*2=6,判断X6在多边形外部,与实际相符。
在图4中,本文算法分别与文献 [12]算法、文献[13]的算法和文献 [7]的算法对比分析见表2。
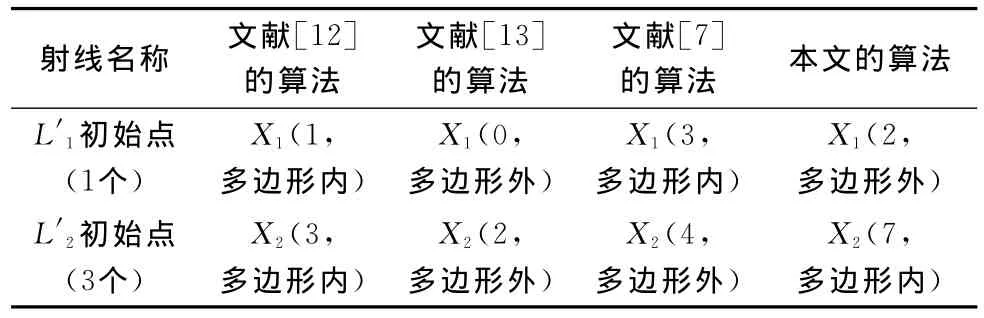
表2 针对图4的4种算法的对比分析结果
(1)L’1初始交点数为1。文献 [12]的算法和文献[7]算法判断X1在多边形内部,与实际都不相符;文献[13]算法判断X1在多边形外部;本文算法计算交点数Cnt=Ci+1*1=2,判断X1在多边形外部,与实际相符。
(2)L’2初始交点数为3。文献 [12]算法判断X2在多边形的内部;文献 [13]算法和文献 [7]算法判断X2在多边形外部,与实际不相符;本文算法计算交点Cnt=Ci+1*1+1*3=7,判断X2在多边形内部,与实际相符。
在图5中,本文算法分别与文献 [12]的算法、文献[13]的算法和文献 [7]的算法对比分析见表3。

表3 针对图5的4种算法的对比分析结果
L1过公共顶点V9,穿过多边形为V7V8V9V3V4,可简化为V7V8V9和V3V4V9两个三角形,初始交点Ci=2,文献 [12]算法、文献 [13]算法和文献 [7]算法判断P在多边形的外部,与实际都不相符;本文的算法按类别 (3)处理,计算交点数Cnt=Ci+1*3=5,判断P在多边形的内部,与实际相符。
从以上算法可知,文献 [1]算法完全不适于图3的空间分布,文献 [13]算法可处理重合线段,文献 [12]和文献 [7]算法对重合线段无法判断。针对图4,文献[12]、文献 [13]和文献 [7]算法都只能正确判断部分的点与多边形的位置关系。针对图5,文献 [12]、文献 [13]和文献 [7]的算法都判断错误。本文的算法能克服文献[12]算法、文献 [13]算法和文献 [7]算法对以上几种特殊情况判断错误而存在的不足,能广泛的应用于各种不同的多边形。既对简单多边形有效,也对复杂多边形有效,并且能准确地判断出点与多边形的位置关系。
5 结束语
在现有射线法研究的基础上,本文提出对顶点加1加2和加3运算,改进并扩展了射线法。该方法首先是分析射线与多边形的边相交的各种情况,然后采用简单的加运算计算交点数以及分析对不同的交点类型进行加运算,最后使用交点数的奇偶性来判断点与多边形的位置关系。4种不同算法分析结果表明,该方法不仅适用简单的多边形,也适合各种类型的复杂多边形,而且能准确判断点与多边形的位置关系。虽然该方法的预处理要花费一些时间,而且预处理时间由于与实验数据的质量和运行环境有较大关系,算法的时间复杂度难以确定,但预处理的结果都会被作为判断条件而反复使用,在应用中有利于提高实际效率,对GIS空间分析和实际应用都有积极的意义,对算法效率的深入研究是下一步的主要工作。
[1]JIANG Ping,LIU Minshi.Improved ray method to judge the relation of point and polygon including simple cure [J].Science of Surveying and Mapping,2009,34 (5):220-222 (in Chinese).[江平,刘民士.射线法判断点与包含简单曲线多边形关系的完善 [J].测绘科学,2009,34 (5):220-222.]
[2]Yang Sheng,Yong Junhai.A point-in-polygon method based on a quasi-closest point [J].Computers& Geosciences,2010,36 (2):205-213.
[3]Juan J Jime′nez,Francison R Feito.A new hierarchical triangle-based point-in-polygon data structure [J].Computers &Geosciences,2009,35 (9):1483-1583.
[4]LIU Liang.An optimized algorithm to determine topo-relation between point and polygon and clockwise or anti-clockwise in polygon [J].Geomatics & Spatial Information Thchnology,2007,30 (1):84-86 (in Chinese). [刘梁.点、多边形拓扑关系与多边形顺、逆判断优化算法 [J].测绘与空间地理信息,2007,30 (1):84-86.]
[5]Jing Li,Wang Wencheng.Point-in-polygon tests by convex decomposition[J].Computers & Graphics,2007,31 (4):636-648.
[6]LI Nan,XIAO Keyan.Improved judgment algorithm of point in-out polygon [J].Computer Engineering,2012,33 (5):30-34(in Chinese).[李楠,肖克炎.一种改进的点在多边形内外判断算法 [J].计算机工程,2012,38 (5):30-34.]
[7]LIU Yabin,LIU Dayou.Reasoning of topology spatial objects in GIS [J].Journal of Software,2001,12 (12):1859-1863 (in Chinese).[刘亚彬,刘大有.地理信息系统中空间对象间拓扑关系的推理 [J].软件学报,2001,12 (12):1859-1863.]
[8]CHEN Shuqiang,CHEN Xuegong.A new method deciding whether a point is in a polygon [J].Microelectronics and Computer,2006,23 (8):194-195 (in Chinese).[陈树强,陈学工.判定检测点是否在多边形内的新方法 [J].微电子学与计算机,2006,23 (8):194-195.]
[9]Luo Guo,Shihong Du.Global and local indicators of spatial association between points and polygons:A study of land use change [J].International Journal of Applied Earth Observation and Geoinformation,2013,21:384-396.
[10]DONG Xiushan,LIU Runtao.New algorithm for determining position relation between simple polygon and point [J].Computer Engineering and Applications,2009,45 (2):185-186(in Chinese).[董秀山,刘润涛.判断点与简单多边形位置关系的新算法 [J].计算机工程与应用,2009,45 (2):185-186.]
[11]XIA Renbo,LIU Weijun.Method for determing whether a certain point is inside a polygon in plane [J].Chinese Journal of Mechanical Engineering,2006,42 (3):130-135 (in Chinese).[夏仁波,刘伟军.点在平面多边形内外的判断方法[J].机械工程学报,2006,42 (3):130-134.]
[12]ZHANG Hong,WEN Yongning.The basic algorithm of geography information system [M].Beijing:Science Press,2006:25-30 (in Chinese).[张宏,温永宁.地理信息系统算法基础 [M].北京:科学出版社,2006:25-30.]
[13]CHEN Ruiqing,ZHOU Jian,YU Lie.Fast method to determine spatial relationship between point and polygon [J].Journal of Xi’an Jiaotong University,2007,41 (1):59-63(in Chinese).[陈瑞卿,周健,虞烈.一种判断点与多边形关系的快速算法 [J].西安交通大学学报,2007,41 (1):59-63.]
