基于灰色关联系数的混合噪声滤波算法
2014-09-10龚声蓉高祝静
赵 敏,龚声蓉,高祝静
(1.南通大学 理学院,江苏 南通226007;2.苏州大学 计算机科学与技术学院,江苏 苏州215006)
0 引 言
噪声滤除是图像预处理的重要环节之一,高斯和脉冲噪声是图像中最常见的两种噪声,常会同时出现,称为混合噪声。针对混合噪声最常用的去噪方法是均值滤波和中值滤波,其中均值滤波主要用于去除高斯噪声,而中值滤波主要用于去除脉冲噪声[1,2]。但两者共同的缺点是对所有像素点采用统一的邻域处理方法,并没有充分利用邻域像素间的局部灰度值差异特性[3]。
灰色理论,是我国学者邓聚龙1982年创立的,是一种研究少数据、贫信息不确定性问题的新方法,已成功地应用于经济、气象、生物、地质勘探、交通运输、过程控制、环境保护等众多领域[4]。应用灰色理论研究图像去噪问题,拓展了原有图像去噪技术的发展空间,也吸引了越来越多学者的关注,其相关研究逐渐成为一个崭新的课题。如文献 [5,6]主要利用灰色理论中的灰色关联理论研究数字图像中椒盐噪声[7](也称为双极脉冲噪声)滤除问题,文献 [8,9]亦利用灰色关联理论分别研究了图像中高斯噪声、混合噪声的滤除问题。这些算法在应用灰色关联理论进行图像去噪方面做了较好的探索,但在实际应用中仍存在一定的局限性。如文献 [5]适用于低密度椒盐噪声,但无法较好地滤除高密度椒盐噪声,针对全白或全黑的区域误判率较高。在充分研究相关算法的基础上,针对文献[5,8,9]中的局限性,本文提出了一种基于灰色关联系数的混合噪声滤波算法,并给出了具体实例进行对比分析。实验结果表明,该算法在多种噪声密度下均具能有效地去除混合噪声,提高图像的峰值信噪比。
1 灰色关联理论基础
灰色关联分析不仅是灰色理论的重要组成部分之一,而且是灰色系统分析、建模、预测、决策的基石[10]。目前在图像处理中,所涉及的灰色关联分析主要是使用灰色关联系数分析图像的邻域信息,降低问题的复杂度,并获得量化结果[10]。在图像处理中,涉及的系统特征序列、系统因素序列往往都是一维向量[5,6,8],因而,相应的灰色关联系数公式可简化为
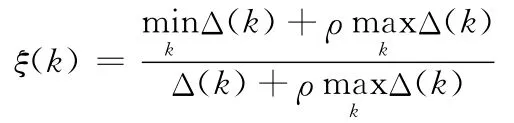
2 基于灰色关联系数的椒盐滤波算法
文献 [5]应用灰色关联理论,使用双阈值进行图像椒盐噪声的滤除,取得了良好的去噪效果。但也存在一定的不足,为此提出了改进的椒盐噪声检测及滤波算法如下:
步骤1 令min[X]、max[X]分别表示加噪后图像的最小灰度值、最大灰度值。以3×3滤波窗口为例,若当前的中心 (i,j)的灰度值为min[X]或max[X],则点(i,j)作为候选噪声点并转至步骤2进一步判断是否为真正的噪声点,否则判断该点为信号点,不做任何改动。
步骤2 寻找点 (i,j)的3×3邻域中灰度值不等于min[X]、max[X]的点以形成一个序列。如果该序列为空,则将窗口动态扩大一圈为5×5,继续搜索满足条件的点,如果该序列仍然为空,则进一步扩大窗口的范围为7×7。若窗口范围为7×7下,仍找不到一个满足条件的点,此时,该中心点 (i,j)及其7×7邻域极可能为全黑或全白的图像块,而非噪声点,统计该点7×7邻域内min[X]与max[X]所占比例,若min[X]所占比例超过0.66,则该7×7区域的灰度值均修改为min[X],若max[X]所占比例超过0.66,则该7×7区域的灰度值均修改为max[X]。
步骤3 如果步骤2中得到的非空序列中的元素都具有相同的数值或仅存在一个元素,则将该值直接赋给中心点(i,j)。如果得到的序列中至少存在两个元素具有不同数值,则令该序列为系统因素序列,该序列的均值为系统特征序列,计算其灰色关联系数。
步骤4 令序列中各元素的灰度关联度系数的中值为med,对序列中关联系数大于med的元素的灰度值取均值赋给中心点。
与文献 [5]的主要差异如下:
(1)统计序列不包括噪声点
为了作对比分析,与文献 [5]取同一个3×3的区域,见表1,整数为灰度值,小数为对应的灰色关联系数。依据文献 [5],此时对应的序列中有9个点,包括窗口中心这一噪声点,其还原值为 (234+234+233+85)/4=196.5。而依据本文算法,所统计的序列有8个点,不包括中心点,中心点的还原值为: (235+234+234+233)/4=234,更接近该点未加噪前的真实值235。由表1(a)、表1(b)对比,还可看出依据本文算法,83、85、87对应的关联系数相对较小,即认为83、85、87与中心点的还原值相关性较小,而文献 [5]却认为85与中心点还原值的相关性高于235对应的相关性。由此可见,本文算法对中心点所在邻域与中心点的相关性刻画更为准确,中心点的还原值估计也更合理。
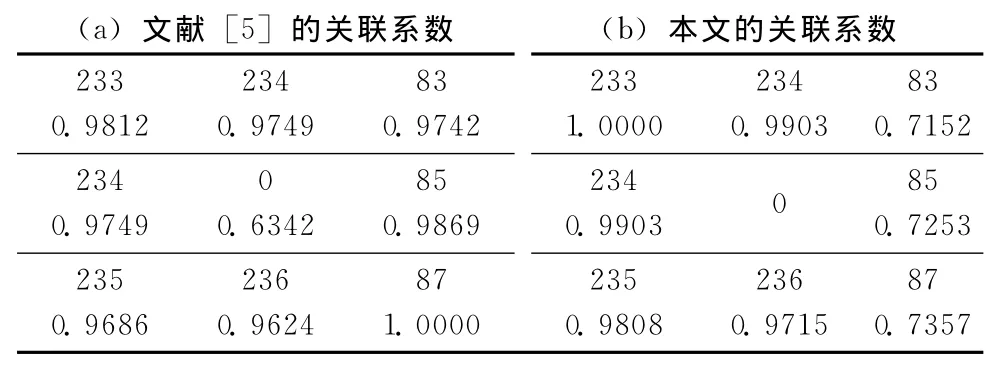
表1 实例1关联系数对比
(2)中心点窗口的动态扩展
当对图像进行高密度椒盐加噪,3×3区域全为噪声点的概率较大。此时,若固定序列的取值范围为3×3邻域,将无法找到中心点的恰当还原值,针对这一情况,采取动态扩大取值窗口的策略。现取lena图中一平坦区域加噪后的图像块进行对比分析,文献 [5]及本文算法对应的关联系数分布见表2,其中心点的还原值分别为0、167.8,相对误差分别为100%、0.7%,本文算法具有更低的相对误差。
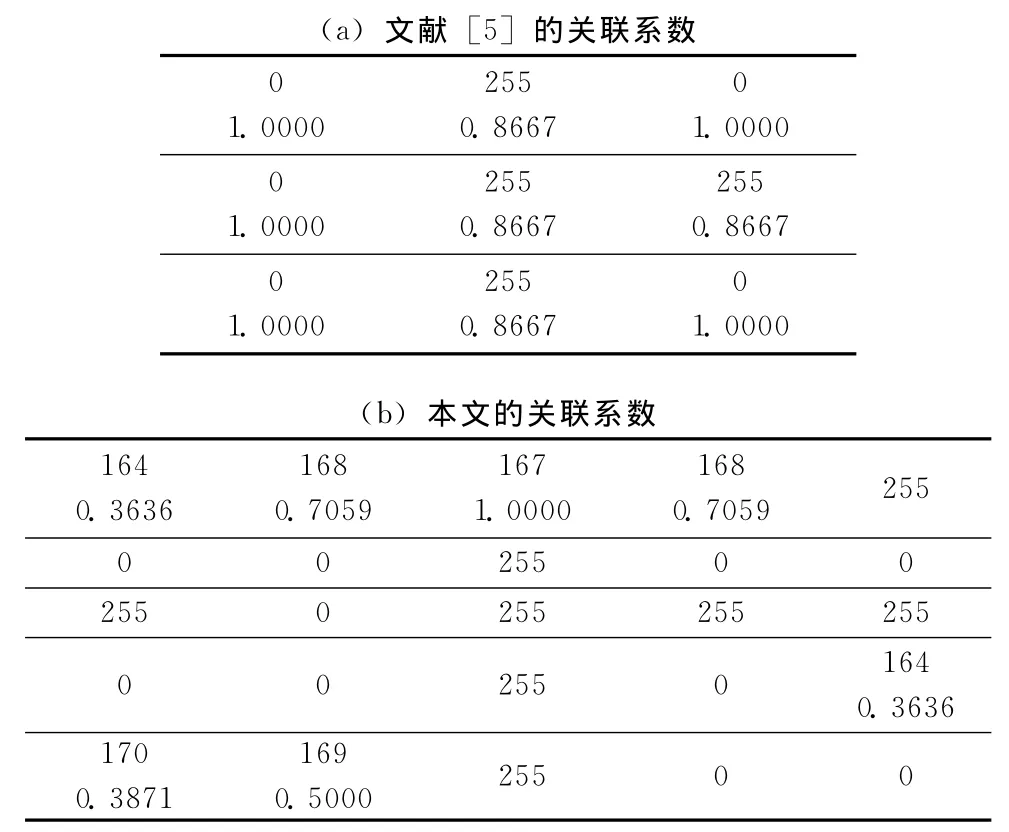
表2 实例2关联系数对比
采用中心点窗口动态扩展的策略能够有效的提高高密度椒盐下的去噪效果,但该策略也会造成误检,共两种情况:①若某3×3图像块未加噪前的灰度值绝大部分为非min[X]或max[X](下以0代表min[X],255代表max[X]),加噪后该块灰度值全为0或255,且0占的比重超过0.66,则该区域的还原值将误判为全0;②若某3×3图像块未加噪前的灰度值全为255,加噪后该块灰度值全为0或255,且0占的比重超过0.66,则该区域的还原值也会误判为全0。若椒盐噪声为0.6,且全0、全255、非0或255区域比例一致下,由概率论中二项分布的知识,易推导3×3的情形下的误判率[11]为0.0238,512×512像素的图像误判点高达6239。
若检测窗口扩大为7×7,其对应的误检点已降到7.24×10-8,误判点仅为0.019,因而在步骤2中选择的最大检测窗口为7×7。由于未加噪lena图灰度值范围为 [34,247],为此,特意在lena图上又添加了全黑或全白的四块区域再进行加噪,如图1(a)所示,图1(b)中白色和黑色区域的还原的误判点基本不存在,算法的误判率优于文献 [5]。

图1 0.4的椒盐噪声去噪效果对比
3 基于灰色关联系数的高斯滤波算法
在椒盐噪声滤除后,使用如下高斯滤波算法进行高斯去噪:
步骤1 令椒盐去噪后的图像为X′,对其进行3×3的均值滤波得到图像X″,将X″中3×3窗口中的9个像素的灰度值作为系统特征序列,对应的X′中的9个像素的灰度值作为系统因素序列,计算其对应的灰色关联系数。
步骤2 求出9个关联系数最小的元素,若该元素为中心点或中心点后面的4个点,即表3(b)中的119、56、128、1、100的位置,则将其在X″中对应的灰度值替换X′中的同一位置元素的灰度值,设替换后的新图像为X。
步骤3 将X中3×3窗口中的9个像素的灰度值作为系统因素序列,9个像素灰度值的均值作为系统特征序列,计算其对应的灰色关联系数,筛除灰色关联系数最小的两个元素,计算剩余的7个元素对应的灰度值均值作为中心点的还原值。
文献 [8,9]均使用3×3窗口中的9个像素的灰度值作为系统因素序列,9个像素灰度值的均值或中值作为系统特征序列,计算其对应的灰色关联系数确定权值,再将各个像素与其对应的权值相乘再相加,即得中心点的还原值分别为97.4、95.1,相对误差为9.8%、11.9%。而依据本文算法,在步骤1中,将均值滤波后的值66取代原来的灰度值1后,再次计算关联系数,见表3(d),得到筛选后对应的关联系数序列有7个点,中心点的还原值为:(95+81+126+112+119+128+100)/7=108.7,具有更小的相对误差0.6%。
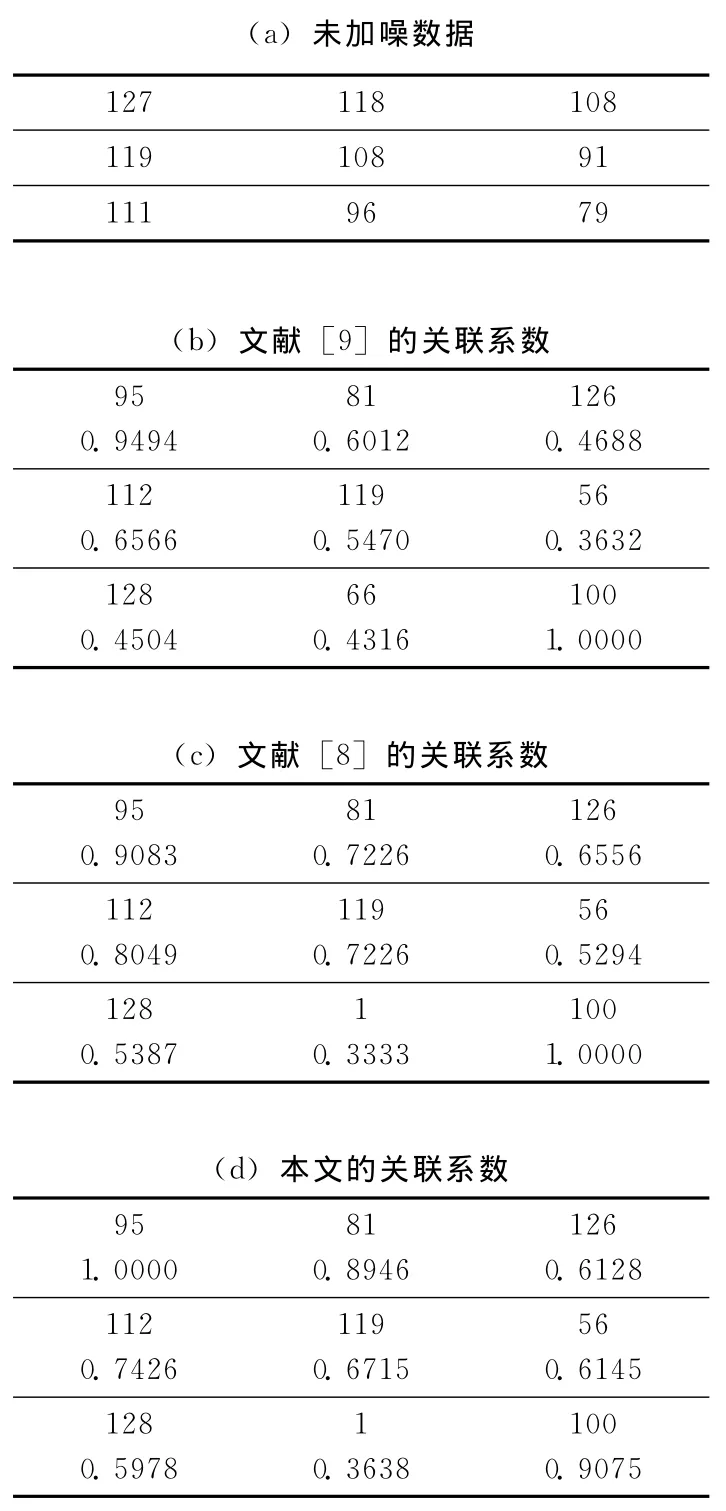
表3 实例3关联系数对比
4 实验结果及分析
(1)椒盐去噪结果分析
表4为将lena图像添加密度为0.2、0.3、0.4、0.5、0.6椒盐噪声后,文献 [5,6]及本文算法去噪后PSNR,本文算法具有更高的PSNR。在加入0.4椒盐噪声或更低密度椒盐噪声的情况下,文献 [5]中的算法,也能较好地去除绝大部分噪声,如图1所示。但加入高密度椒盐噪后,去噪效果并不理想,仍有许多噪点没有去除干净,如图2(b)所示,而本文算法却能将噪点基本去除干净,并取得较好的视觉效果,如图2(d)所示。相对于高密度噪声情况,与文献 [5,6]相比,优势更加明显。

图2 0.6的椒盐噪声去噪效果对比
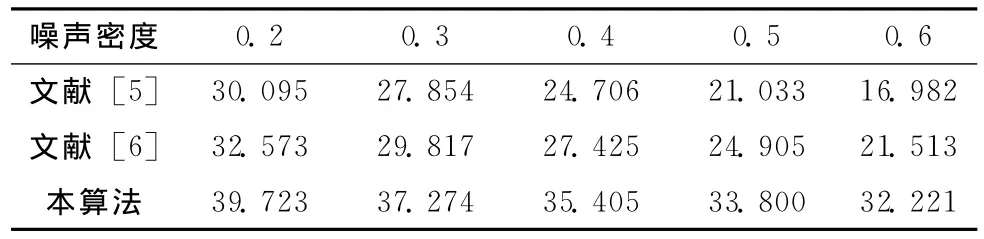
表4 各种滤波算法在不同噪声密度下的PSNR值比较
(2)高斯去噪结果分析
图3为高斯噪声方差σ=0.02、椒盐噪声密度P=0.2下,不同灰色关联去噪算法降噪的效果对比图,从主观感觉上可以看出,本文的混合滤波效果优于文献[8,9]。表5以PSNR这一滤波效果客观评价指标,定量的反映出3种算法在不同混合噪声下的滤波效果差异。通过表5可以看出就文献 [8,9]而言,在高斯噪声方差较大的情形下,文献 [8]去噪效果优于文献[9];在高斯噪声方差、椒盐密度均较小的情形下,文献 [9]又优于文献 [8]。而本文算法在各种混合噪声下均具有较高的PSNR,表明本算法可以更为有效地滤除混合噪声,具有更优的滤波效果。

表5 不同混合噪声下的不同算法滤波后的PSNR

图3 σ=0.02、P=0.2混合噪声去噪效果对比
5 结束语
本文在灰色关联理论的基础上,提出了一种基于灰色关联系数的混合噪声滤波算法。算法分为椒盐去噪及高斯去噪两部分,其中椒盐去噪部分采用了有选择的统计灰色关联系数及中心点窗口动态扩展的策略,高斯去噪部分又充分利用均值滤波后的数据筛选相关点的灰度值,从而更为合理地计算还原值。实验结果表明,在不同的混合噪声干扰下,本算法滤波后的图像不仅在滤波性能客观评价指标上均明显优于多种灰色关联去噪算法,而且在主观视觉效果方面亦能有效提高图像的清晰度,为研究灰色关联理论滤除混合噪声提供一种有效的途径。
[1]HOU Yanli.An efficient algorithm for mixed noise removal in image [J].Journal of Henan University (Natural Science),2011,41 (2):197-201 (in Chinese). [侯艳丽.一种有效的去除图像混合噪声的算法 [J].河南大学学报 (自然科学版),2011,41 (2):197-201.]
[2]Toprak A,Guler I.Suppression of impulse noise in medical images with the use of fuzzy adaptive median filter [J].Journal of Medical Systems,2006,30 (6):465-471.
[3]WANG Yiyan.A filtering algorithm for removing mixed image noise [J].Computer Applications and Software,2010,27(17):97-102 (in Chinese).[王益艳.一种去除图像混合噪声的滤波算法 [J].计算机应用与软件,2010,27 (17):97-102.]
[4]LIU Sifeng,DANG Yaoguo,FANG Zhigeng,et al.The grey system theories and application [M].5th ed.Beijing:Science Press,2010(in Chinese).[刘思峰,党耀国,方志耕,等.灰色系统理论及其应用 [M].5版.北京:科学出版社,2010.]
[5]ZHANG Suwen,CHU Naiqiang.A filtering algorithm based on grey correlative degree for salt-pepper noise images [J].Infrared Technology,2008,30 (11):651-654 (in Chinese).[张素文,褚乃强.一种基于灰色关联度的椒盐噪声滤波算法[J].红外技术,2008,30 (11):651-654.]
[6]YANG Fangfang,ZHANG Youhui,WANG Zhiwei,et al.Image median filtering algorithm based on grey absolute relation[J].Journal of Computer Applications,2011,31 (12):3357-3359 (in Chinese). [杨芳芳,张有会,王志巍,等.基于灰色绝对关联度的图像中值滤波算法 [J].计算机应用,2011,31 (12):3357-3359.]
[7]Lu Ching-Ta,Chou Tzu-Chun.Denoising of salt-and-pepper noise corrupted image using modified directional-weighted-median filter [J].Pattern Recognition Letters,2012,33 (10):1287-1295.
[8]LI Yanling,HUANG Chunyan,ZHAO Juan.An adaptive algorithm for median filter of image based on grey relation [J].Computer Simulation,2010,27 (1):238-240 (in Chinese).[李艳玲,黄春艳,赵娟.基于灰色关联度的图像自适应中值滤波算法 [J].计算机仿真,2010,27 (1):238-240.]
[9]ZHAO Yaliang,FANG Caili,XUE Changsong,et al.An adaptive filter approach for removal of mixed noise based on grey relevance and MTM algorithm [J].Journal of Henan University (Natural Science),2011,41 (5):515-518 (in Chinese).[赵雅靓,房彩丽,薛长松,等.基于MTM和灰色关联度的混合噪声自适应滤波算法 [J].河南大学学报 (自然科学版),2011,41 (5):515-518.]
[10]MA Miao,ZHANG Yanning,ZHAO Jian.The grey theories and application in image engineerinG [M].Beijing:Qinghua Press,2011(in Chinese).[马苗,张艳宁,赵健.灰色理论及其在图像工程中的应用 [M].北京:清华大学出版社,2011.]
[11]CHEN Chuxia,DING Yong,LIU Lili.Adaptive switch weighted mean filtering for salt and pepper noise removal [J].Computer Engineering,2010,36 (4):210-212 (in Chinese).[陈初侠,丁勇,刘栎莉.去除椒盐噪声的自适应开关 加 权 均 值 滤 波 [J]. 计 算 机 工 程,2010,36 (4):210-212.]
