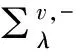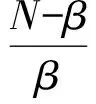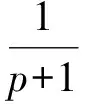积分方程组解的正则性与对称性

王长森，林国炜

(江西师范大学数学与信息科学学院，330022，南昌)

积分方程组解的正则性与对称性

王长森，林国炜

(江西师范大学数学与信息科学学院，330022，南昌)

将讨论下列含贝塞尔核积分方程组正解的对称性，即：

(1)

(2)

设(u,v)∈Lp+1(RN)×Lq+1(RN)为式(1)的正解，则式(1)解是径向对称的。

积分方程组；贝塞尔核；径向对称

0 引言

本文将讨论下列含贝塞尔核积分方程组正解的对称性，即：

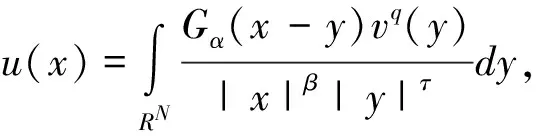
(3)

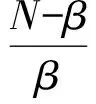
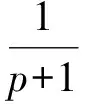
(4)

特别的，当u=v,p=q,β=τ=0时，式(3)简化成：

(5)

在文献[8]中，对于贝塞尔势能的sobolevinepuality(Bα(f)=Gα*f,α>0;Bα(f)=f,α=0,这里*表示函数间的卷积)：

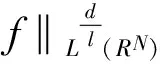
(6)

当β=τ=0时，在文献[9]中讨论了方程组(3)正解的径向对称性，同时也讨论了当α=2,β=τ=0时解的唯一性。如果β≠0,τ≠0时，在文献[9]中建立了关于贝塞尔势能带双权Hardy-Littlewood-Sobolevinequality，即：

(7)

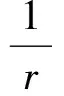
在文献[6]中已证出下面积分方程组：

(8)

正解的径向对称性和局部Hölder连续性。

式(3)是关于式(7)的Euler-Lagrange方程。为了得到不等式式(7)中的最佳常数，定义最大函数：

在‖f‖r=‖h‖s=1的条件下，则对应的Euler-Lagrange方程为下面积分方程组：

(9)

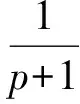
当贝塞尔核Gα(x)可以被Riesz核替代时，则式(3)就化成：

(10)

(11)

在文献[4]中，通过移动平面法已证出方程组(10)正解的径向对称性。此外，研究者也采用在文献[7]中的正则性提升方法，得出理想的积分区间和渐近性，读者可以查阅在文献[1-3,5,7,13-14]中更多的应用。

本文主要讨论在式(4)条件下，式(3)正解的径向对称性，即：在(u,v)∈Lp+1(RN)×Lq+1(RN)为式(3)的正解，则解(u,v)是径向对称的。

1 引理及其命题

对于任意的实数λ，定义：∑λ={x=(x1,x2,…,xN)∈RN|x1≤λ},Tλ={x∈RN|x1=λ}。对于x∈∑λ，令xλ=(2λ-x1,x2,…,xN)，定义：uλ(x)=u(xλ),vλ(x)=v(xλ)。

引理1：对于式(3)的任意正解，有：

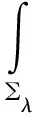
(12)

(13)

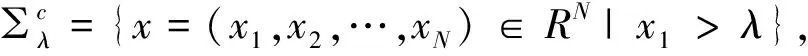
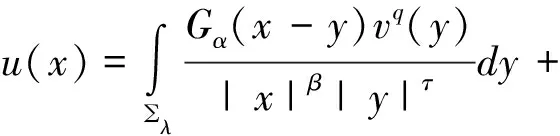
在上等式中应用了在RN中Gα是径向对称的，即有|xλ-y|=|x-yλ|，在上等式中x用xλ代替有：

因此，

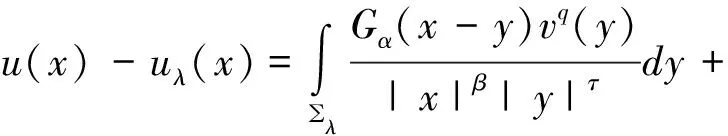
同理，v(x)-vλ(x)也是成立的。证毕。

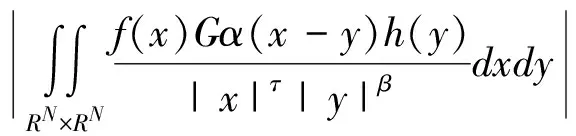
(14)

(15)

此命题的证明可参考文献[6]。

2 主要结果及其证明

在这一部分，应用上述的引理及其命题证明出本文的主要结果，将采用文献[2]中的移动平面法来证明本文的主要结果，本文主要结果如下。

定理1：设(u,v)为式(3)的任意一个正解，则此解是径向对称的，并且关于RN中某些点是单调递减的。

证明：首先，证明对于充分小的负数λ，有：

u(x)≤u(xλ),v(x)≤v(xλ),∀x∈∑λ

(16)

事实上，令：

通过对最新脑科学研究成果的解读，我们可以看到脑科学的研究已经走到了与其他多学科交叉的关键时刻，而且物理、化学等多种方法在脑科学研究中的运用一再突破脑科学的极限，使最终观测大脑实时活动成为可能。

wλ(x)=u(x)-u(xλ),zλ(x)=v(x)-v(xλ)。

以及，

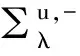
由于，

|x-y|<|xλ-y|,|y|>|yλ|,∀x,xλ,yλ∈∑λ，

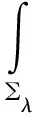
根据p,q>1以及式(4)知：

(17)

选择合适的d1,d2使得：

(18)

由式(4)可知：

(19)

因此，由命题1及Höler不等式可推出：

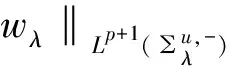
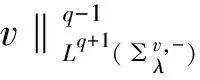
(20)

以及，

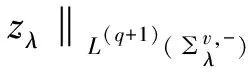
(21)

所以，

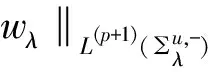
(22)

根据(u,v)∈Lp+1(RN)×Lq+1(RN),对于充分小的的负数λ，有：

因此有：

接下来，连续的增大λ的值，也就是说，在式(13)成立的条件下，将平面Tλ往右平移。下面将证明通过这样移动平面Tλ，这种平移直到刚好平移到原点才停止。

事实上，令：

λ0=sup{λ|u(x)-uλ(x)≤0,v(x)-vλ(x)≤0,∀x∈∑λ}

(23)

显然λ0≤0,接下来断言：

λ0=0

(24)

事实上，若λ0<0,则存在x0,x1∈∑λ0,使得：u(x0)=uλ0(x0),v(x1)=vλ0(x1)。由引理1及xλ0=(x0)λ0有：

根据在∑λ0中，有|x0|>|xλ0|,|y|>|yλ0|,所以，在∑λ0中有：

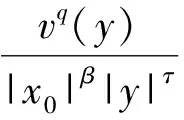
此外，在∑λ0中还有|x0-y|<|xλ0-y|，从而可知：

v(x)=vλ0(x)=0,a.e.x∈∑λ0

也就有v(x)≡0,这与v是正数就相矛盾，所以有：

u(x)

同理可证：

v(x)

由(u,v)∈Lp+1(RN)×Lq+1(RN),则对∀ε>0,∃R>0,使得：

由Lusin定理知，对∀δ>0,∃一个闭集Fδ满足Fδ⊂BR(0)∪∑λ0=E,m(E-Fδ)<δ,使得wλ0|Fδ,zλ0|Fδ是连续的。

在∑λ0中有wλ0,zλ0<0,在Fδ中有wλ0,zλ0<0。选择ε0>0并充分的小，使得对∀λ∈[λ0,λ0+ε0)，在Fδ中有wλ,zλ<0，对于这样的λ有：

选择充分小的ε,δ,ε0，使得：

因此，

另一方面，采用同样的方式，可将平面从x1方向的正无穷远处往x1=0平移，这样可得u(x),v(x)关于x1=0是径向对称及单调递减的。此外，x1的方向可以是任意选取的，所以u(x),v(x)关于原点是径向对称的及严格单调的。证毕。

[1] Chen W,Li C.Regularity of solutions for a system of integral equations[J].Comm Pure Appl Anal,2005,4:1-8.

[2]Chen W,Li C,Ou B.Classification of solutions for an integral equation[J].Comm Pure Appl Math,2006,59:330-343.

[3]Chen W,Li C,Ou B.Classification of solutions for a system of integral equations[J].Comm PDE,2005,30:59-65.

[4]Jin C,Li C.Symmetry of solutions to some systems of integral equations[J].Proc Amer Math Soc,2006,134:1661-1670.

[5]Jin C,Li C.Qualitative analysis of some system of integral equations[J].Calc Var PDE,2006,26:447-457.

[6]Chen X,Yang J.Regularity and symmetry of positive solutions of an integral system[J].Acta Math Sci,2012,32B:1759-1780.

[7]Chen W,Jin C,Li C,etal.Weighted Hardy-Littlewood-Sobolev inequalities and systens of Integral equations[J].Disc Cont Dyn Sys,2005,suppl:164-172.

[8]Ma L,Chen D.Radial symmetry and montonicity for an integral equation[J].J Math Anal Appl,2008,342:943-949.

[9]Ma L,Chen D.Radial symmetry and uniqueness for positive solutions of a Schrõ dinger type Systems[J].Mathematical and Computer Modelling,2009,49:379-385.

[10]Ma L,Zhao L.Uniqueness of ground states of some coupled nonlinear Schrödinger systems and their application[J].J Diffe Equa,2008,245:2551-2565.

[11]Stein E,Weiss G.Fractional integrals in n-dimension Euclidean spaces[J].Journ Math Mech,1958,7:503-514.

[12]Li Y.Remark on some conformlly invariant integral equations:The method of moving spheres[J].J Eur Math Soc,2004,6:153-180.

[13]Xu J,Tan Z.Classification of solutions for a class of singuar integral system[J].Acta Mathematica Scientia,2011,31:1449-1456.

[14]Zhao Y,Lei Y.Asymptotic behavior of positive solutions of a nonlinear integral system[J].Nonlinear Anal,2012,75:1989-1999.

RegularityandSysmmetryofSolutionsofanIntegralSystems

WANG Changsen,LIN Guowei

(Jiangxi Normal University.College of Mathematic and Information Science,330022,Nanchang,PRC)

In this paper,we are concerned with symmetry of solutions of the following nonlinear integral system：

(1)

(2)

Let (u,v)∈Lp+1(RN)×Lq+1(RN) be a positive solution of(1).We show that the solution of(1) is symmetric.

integral system;bessel kernel;radially symmetry

2014-07-15;

2014-09-09

王长森(1989-)，男，江西上饶人，硕士研究生，主要从事带权的积分方程的研究。

国家自然科学基金项目(编号:11361029)；江西省教育厅科学技术研究项目(编号:GJJ14270)。

10.13990/j.issn1001-3679.2014.05.002

O175.2

A

1001-3679(2014)05-0573-05