基于均匀七次B样条插值求解动力响应的逐步积分法
2014-09-08蹇开林温伟斌骆少明
蹇开林,温伟斌,,骆少明
(1. 重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆 400044; 2. 仲恺农业工程学院,广州 510225)
时间积分方法为求解结构动力响应尤其大型结构有限元离散计算的有效手段,该方法需在每个时间步上离散化求解平衡方程;而非线性分析中则需在每个时间步上进行迭代运算并更新系统刚度矩阵,对自由度数较大系统计算量较大。因此,研究时间积分方法时不仅考虑算法的稳定性质,亦应考虑计算精度及效率,期望以较少时间步计算获得高精度数值解。逐步积分法可分显式积分法[1-3]与隐式积分法[4-6]两类。前者优点在于无需对每个时间步的平衡方程迭代运算,计算量少,且易于编程实现[7]。其不足之处在于大多数方法均为条件稳定,计算结果连续性低,需采用较小时间步计算才能获得稳定、足够精度的计算结果。由于显式积分法算法实现上较隐式积分法简单,已被用于拟动力试验研究[8-10]。分段样条多项式插值近似已被用于计算机辅助设计、几何造型、数据拟合及有限元计算[11-12]。Liu[13]用分段Birkhoff插值多项式求解多自由度系统动力响应;Inoue等[14]给出基于正交B样条多项式的逐步积分格式, 相比传统Newmark法、Wilson-θ法,该方法计算程序简单、效率更高。Rostami等[15]用四次B样条基函数发展的具有抛物线加速度的显式积分法,但其条件为稳定的。张琳等[16]在Hamilton型拟变分原理体系下建立时间子域以三、五次B样条函数插值的时间子域法,但其前处理计算量较大。
鉴于显式积分法算法稳定性与计算精度的不足,本文提出参数控制的逐步积分法。该方法采用均匀七次B样条插值建立节点位移、速度、加速度试函数,给出平衡递推方程;通过控制参数可使算法绝对稳定。数值算例结果表明,数值位移、速度、加速度计算精度较高。
1 均匀七次B样条
本文采用B样条基函数插值离散化求解结构动力问题微分方程,B样条基函数有多种定义方法,为便于计算机编程,用逆推方法定义[12]。设{t0,t1,…,ti,ti+1,…}为单调不减序列,即,ti≤ti+1,(i=0,1,2,…)。其中ti为B样条节点。取Bi,k(t)为第i条k次B样条曲线,定义为
(1)
(2)
式中:[ti,ti+1)为第i个B样条节点区间。逆推过程中,需约定0/0=0。
对均匀B样条基函数取ti+1-ti=Δt,τi=(t-ti)/Δt,则由逆推定义可推导t∈[ti,ti+1)内,插值所用七次均匀B样条基函数及导数表达式为
(3)
(4)
8(2-τi)7-l+28(1-τi)7-l]
(5)
28(2-τi)7-l-56(1-τi)7-l]
(6)
(7)
(8)
(9)
(10)
式中:l为各B样条基函数对t的导数阶次。
2 基本原理及算法实现
2.1 动力平衡方程递推格式
单自由度系统结构动力学微分方程可写为

(11)
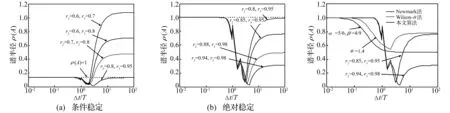
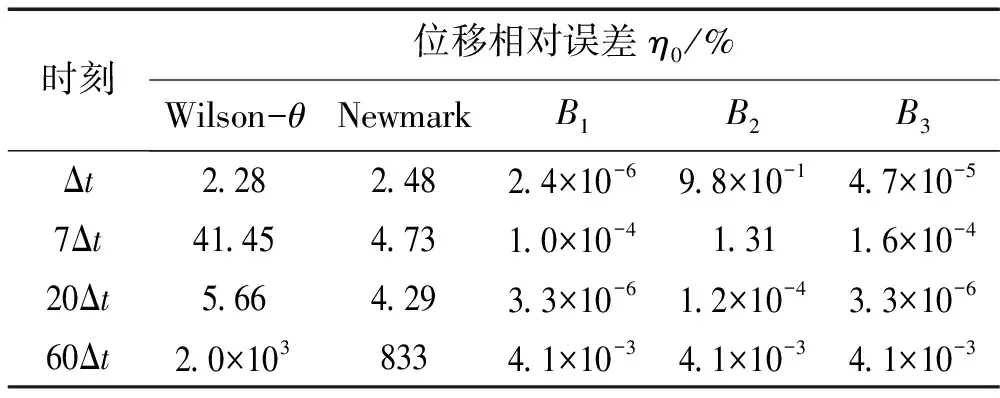
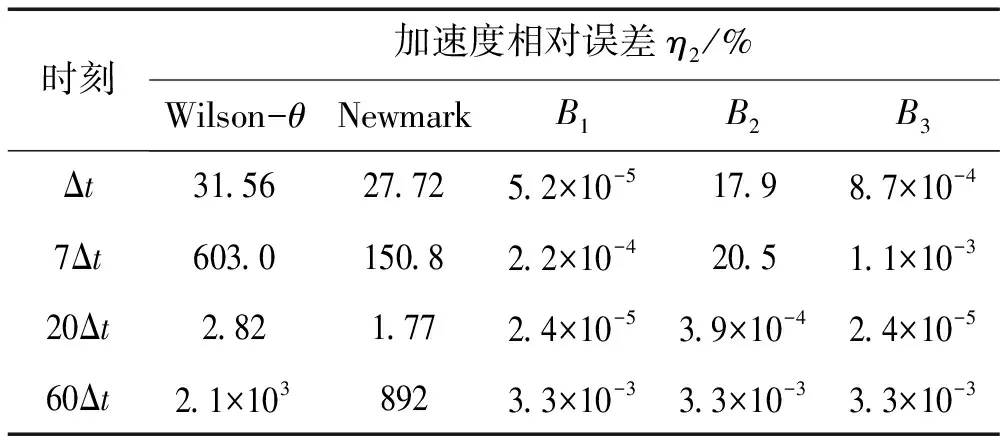
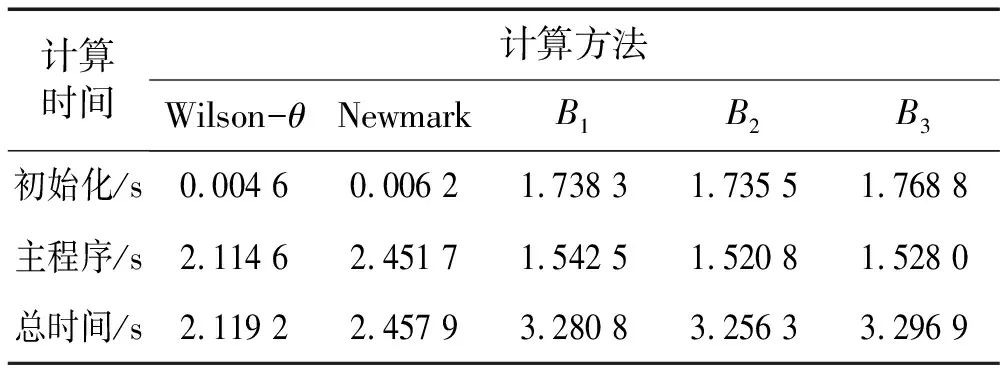
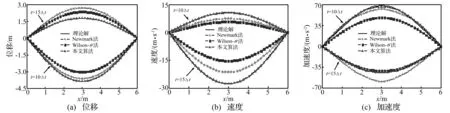
取0=t0<… x(l)(t)=B(l)(τi)di (12) 式中: (14) 为便于推导,令 (15) (16) (17) 由式(12)有 (18) 式(18)可写为矩阵形式 (19) 式中: (20) (21) 将式(19)代入式(12)有 (22) 将式(22)代入式(11)得残值方程为 (23) 令 (24) 将式(24)代入式(23)有 (25) 取权函数W1(τi)=δ(τi-1),W2(τi)=δ(τi-r1),W3(τi)=δ(τi-r2),W4(τi)=δ(τi-r3)。即在点τi=1、τi=r1、τi=r2与τi=r3处采用配点法。其中r1,r2,r3满足r1≠r2≠r3,用以调节计算稳定性与精度。 将式(25)利用加权残值法,得 (26) 将上式运算简化为 (27) 式(27)表明本文算法构造的逐步积分法具有自起步、无中间计算环节特点。 mx(3)(t)+cx(2)(t)+kx(1)(t)=f(1)(t) (28) 令式(28)中t=t0,有 x(3)(t0)=m-1[f(1)(t0)-kx(1)(t0)-cx(2)(t0)] (29) 式(29)为计算x(3)(t0)的直接初始化方法。 (30) (31) 由计算步骤知,矩阵A,Fi的计算会较大程度影响计算效率。式(24)中E(τi)为矩阵A,Fi的主要计算部分。考虑对任意等距时间单元采用相同系数r1,r2,r3,因而对不同时间步无需重复计算,尤其自由度较大系统,亦无需对E(τi)进行大量重复计算, 只需将式(24)中m,c,k替换为对应矩阵,并引入Kronecker乘积运算即可。其它计算过程与单自由度系统类似。由此分析表明本文算法计算量不大。 以单自由度微分方程(T/2π)2x(2)(t)+x(t)=0考察算法的稳定性,其中T为周期。若式(27)中传递函数矩阵A满足谱半径ρ(A)≤1,则算法是稳定的。式(27)中矩阵A(r1,r2,r3)会随r1,r2,r3的取值变化。为便于分析及工程应用,本文取r1=0.9。通过数值计算绘出ρ(A)随Δt/T变化曲线见图2。由图2(a)看出,0 图2 本文算法不同参数r对应谱半径 本文算法与传统Newmark方法、Wilson 方法谱半径见图3。由图3曲线对比知,本文算法对低频段具有更好的保持作用,能有效滤掉高频分量。考虑工程应用中有限元网格计算的高频分量往往不准确,且对结构相应贡献较小,因而可通过增大参数r2,r3能快速有效滤掉高频分量。 表1 不同方法所求位移及相对误差 基于Hamilton拟变分原理建立的B样条时间积分法进行动力学分析计算[16],给出的三次B样条插值计算精度仅为传统方法(Newmark法,Wilson-θ法)的1/17~2/5;而采用五次B样条计算时虽精度有所提高,但前处理复杂、计算量大、计算效率低,与本文算法推导及数据对比可知,本文方法的算法实现与计算精度具优越性。 表2 不同方法所求速度相对误差 表3 不同方法所求加速度相对误差 表4为相同MATLAB编程环境下,取时间步数Nt=60 时各方法计算时间。由表4看出,本文算法的初始化时间远高于传统方法,而主程序计算时间少于传统方法,虽总的计算时间多于传统方法,但计算精度远高于传统方法,计算效率仍较高。 表4 不同方法计算时间对比 图4为两端简支等截面梁,长L=6 m, 截面厚h= 2×10-2m, 截面宽b=2×10-2m, 截面面积A=bh,截面惯性矩I=bh3/12, 弹性模量E=210 GPa,泊松比μ=0.3, 密度ρ=4×104kg/m3, 阻尼系数c=0,横向载荷q(x,t)=F0sin(ω0t)δ(x-L/2),F0=1 kN,ω0=4 Hz。该载荷作用下,简支梁振动位移理论解为 图4 简支梁弯曲振动示意图 取时间步长Δt=0.2 s,空间离散采用三次Hermite有限单元,空间单元数Ns=10。本文算法参数选r2= 0.85,r3=0.95,其它参数同前。简支梁不同时刻位移、速度、加速度曲线见图5。由图5看出,相同时间步长时本文算法计算结果与理论解吻合较好,明显优于传统Wilson-θ法、Newmark法。 简支梁中点(最大变形处)t=iΔt(i=0,1,…,40)时刻计算值见图6。由图6看出,传统方法计算结果在初始时间段与理论解基本吻合,但随时间的增加逐渐偏离理论曲线,结果不准确。而本文算法随时间的增加与理论解吻合仍较好。 图5 给定时刻不同方法数值解 图6 中点位置不同方法数值解 用不同方法计算时间对比见表5。其中C1为取参数r2=0.80,r3=0.95;C2为取参数r2=0.85,r3=0.95;C3为取参数r2=0.88,r3=0.95;均采用直接初始化方法。由表5知,虽本文算法初始化时间远多于传统方法,但总计算时间远少于传统方法、计算精度远高于传统方法,表明本文算法计算效率高,优越性明显。 表5 不同方法计算时间对比 (1) 本文基于均匀七次B样条基函数,通过对任意局部时间域位移、速度、加速度插值构造,推导出逐步积分法逆推格式与计算流程。 (2) 本文算法具有自起步、无中间计算环节特点。对低频部分具有较好保持作用,可通过选取合适参数灵活控制高频段衰减速度。 (3) 由数值试验给出算法绝对稳定参数条件。由本文方法所求位移、速度、加速度计算精度均较高。 [1] Mullen R,Belytchko T. An analysis of an unconditionally stable explicit method[J]. Computers and Structures, 1983,16(6): 691-696. [2] Gérard R, Soive A, Grolleau V. Comparative study of numerical explicit time integration algorithms[J]. Advances in Engineering Software,2005,36(4):252-265. [3] Chang S Y. A new family of explicit methods for linear structural dynamics[J]. Computers and Structures,2010, 88(11/12):755-772. [4] Tamma K K, Zhou X, Sha D. A theory of development and design of generalized integration operators for computational structural dynamics[J]. International Journal of Numerical Methods in Engineering,2001, 50(7): 1619-1664. [5] Zhou X,Tamma K K. Design, analysis and synthesis of generalized single step solve and optimal algorithms for structural dynamics[J]. International Journal of Numerical Method in Engineering, 2004, 59(5): 597-668. [6] Leontiev V A. Extension of LMS formulations for l-stable optimal integration methods withu0-v0overshoot properties in structural dynamics: the level-symmetric (LS) integration methods[J].International Journal for Numerical Methods in Engineering, 2007,71(13):1598-1632. [7] Dokainish M A, Subbaraj K. A survey of direct time integration methods in computational structural dynamics. I. explicit methods[J]. Computers and Structures,1989, 32(6):1371-1386. [8] Shing P B, Mahin S A. Elimination of spurious higher-mode response in pseudo-dynamic tests[J]. Earthquake Engineering and Structural Dynamics, 1987, 15(4): 425-445. [9] Chang S Y. Improved numerical dissipation for explicit methods in pseudo-dynamic tests[J].Earthquake Engineering and Structural Dynamics,1997,26(9):917- 929. [10] Chang S Y. Explicit pseudo-dynamic algorithm with unconditional stability[J].Journal of Engineering Mechanics, 2002, 128(9): 935-947. [11] Piegl L, Tiller W. The Nurbs book[M]. New York: Springer-Verlag, 1997. [12] Sevilla R, Fernandez-Mendez S, Huerta A. Nurbs-enhanced finite element method(NEFEM)[J]. Archives of Computational Methods in Engineering, 2011, 18(4): 441-484. [13] Liu J L. Solution of dynamic response of framed structure using piecewiseBirkhoff polynomial[J]. Journal of Sound and Vibration, 2002, 251(5): 847-857. [14] Inoue T,Sueoka A. A step-by-step integration scheme utilizing the cardinal B-splines[J]. JSME International Journal, 2002, 45(2): 433-441. [15] Rostami S, Shojaee S, Moeinadini A. A parabolic acceleration time integration method for structural dynamics using quartic B-spline functions[J]. Applied Mathematical Modelling, 2012, 36(11): 5162-5182. [16] 张琳,聂孟喜,仝辉. 三次和五次B样条函数在动力响应分析中的应用[J]. 清华大学学报(自然科学版)2006, 46(3): 327-330. ZHANG Lin, NIE Meng-xi, TONG Hui. Cubic and quintic B-spline functions for dynamic response[J]. Tsinghua Univ(Sci. & Tech.), 2006,46(3):327-330.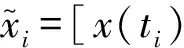
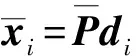
2.2 递推平衡方程初始化
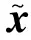
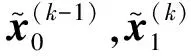
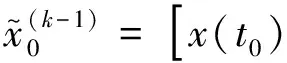
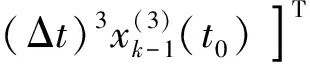
2.3 计算步骤
3 稳定性分析
4 数值算例与分析
4.1 单自由度强迫振动

4.2 简支梁弯曲振动
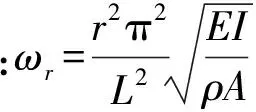



5 结 论
