基于内模原理的舰载雷达稳定平台控制研究

庄文许，张 毅，翁健光

(中国船舶重工集团公司第七二四研究所，南京 211153)

基于内模原理的舰载雷达稳定平台控制研究

庄文许，张 毅，翁健光

(中国船舶重工集团公司第七二四研究所，南京 211153)

舰载雷达稳定平台具有两个自由度，分别用于补偿舰体的纵横摇角度，同时还要克服摇摆运动导致的惯性力矩。此外，负载惯量随天线转动而变化。舰船的摇摆运动可以看作由若干正弦信号叠加而成。针对一类已知频率信息的摇摆运动，设计了基于内模原理的控制律。仿真结果表明，该控制律补偿舰体耦合扰动效果明显，系统稳态跟踪误差指数收敛至原点，且对摇摆运动的振幅、相位和负载转动惯量具有较强的鲁棒性。

舰载雷达；稳定平台；内模原理；鲁棒性

0 引 言

现代军事需求对舰载雷达系统的扫描精度和稳定性提出了较高要求。某雷达结构采用两自由度稳定平台分别补偿舰体的纵向和横向摇摆运动。在舰载雷达伺服系统中，一个突出问题是舰体的纵横摇摆从动力学和运动学两个方面影响伺服控制器的性能。由于自适应内模的发展[1-3]和观测器理论的应用[4,6]，内模控制在舰船设备的伺服系统中得到了广泛应用。Marconi和Isidori等将文献[1]和[2]的成果应用到舰载飞行器自动降落控制中，控制飞行器在安全高度与甲板同步振荡后，实现了飞行器的安全降落[5]；Messineo等在海洋起重机的研究中，通过对标称内模引入自适应观测器和外部干扰预测模型，获得了稳定的提升过程[6]。

舰船的倾斜摇摆可以看作是中性稳定的，内模原理在控制系统中用于构造系统的前馈控制量，使(最小相位)系统的状态轨迹沿着零误差流形滑动，进而获得良好的跟踪性能。本文针对一类已知频率信息但相位和幅值均未知的输入信号，即舰艇的摇摆运动，设计了基于内模原理的控制律。理论证明了系统跟踪误差将渐近收敛到零点，数值仿真验证了所设计控制律的有效性。

1 问题描述

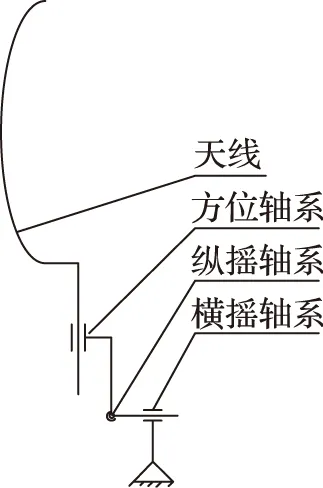
图1 三自由度天线稳定平台传动原理图

三自由度天线稳定平台是舰载雷达的常见形式之一，传动原理图如图1所示，其中横摇轴系和纵摇轴系分别用于补偿舰艇在横向和纵向的摇摆运动，这两个轴系的伺服控制原理是一样的；方位轴系用于带动天线进行方位转动。本文的目的是设计纵横摇轴系的控制律，使得天线始终处于水平状态。

为描述方便，考虑横摇轴系耦合干扰的补偿控制问题。如图2所示，横摇轴系的中心对称面和xy平面平行，舰体的摇摆运动垂直于z轴。假定θf是横摇轴系与舰艇甲板基准平面的夹角，其导数为ωf，θc是舰艇的横摇角度，均逆时针为正；执行机构为交流永磁同步电机(PMSM)，通过减速器带天线转动，同步电机工作在速度环，速度环控制框图如图3所示。假设当天线在全局坐标系中位于水平状态时，负载重心与横摇轴系位于同一铅垂线上，用x1表示θf，x2表示x1的导数，x3为伺服电机绕组电流，则系统的数学模型表示为

(1)

图2 横摇轴系示意图

图3 速度环控制框图

舰体的摇摆运动可以看作由固定频率范围内若干振幅、频率和相位均未知的正弦信号叠加，表示为

(2)

式中，θ=col(θ1-1,θ1-2,θ2-1,θ2-2,…,θN-1,θN-2)，θc是舰体的横摇角度，Γ=[1,0,…,1,0]1×2N，而

被控对象输出为y=x1，跟踪误差定义为e=y+θc。

本文的任务是设计基于内模原理的控制律，使得被控系统(1)在摇摆信号(2)的作用下系统各状态量的轨迹是有界的，且有limt→∞e(t)=0。

2 内模控制器设计

2.1 算法描述

上述描述的问题可以重述为如下形式的系统：

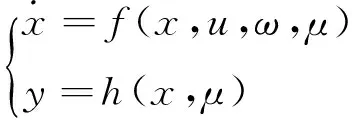
(3)

渐近跟踪或者补偿如下形式的外部参考信号：

yref=r(ω)

(4)

其中ω为如下中性稳定线性时不变微分方程组的解：

(5)

输出调节问题可解的必要条件是针对被控对象(3)和外部系统(4)～(5)有如下假设：

假设1 对于任意给定σ，存在x=πσ(ω,μ)，u=cσ(ω,μ)，且有πσ(0,μ)=0，cσ(0,μ)=0，满足如下方程组：

(6)

假设2 令u=cσ(ω,μ)为系统(5)的输出，存在Φσ和Γ，且(Φσ,Γ)是可观测的，使得系统(5)和u=cσ(ω,μ)可以浸入如下系统：

(7)

假设1和假设2是系统(3)输出调节问题可解的必要条件，式(7)被称为规范化内模控制器，内模原理叙述为：如果(Φ,Γ)是可观测的，任意取定Hurwitz矩阵F和向量G，使得(F,G)是可控的，则存在唯一非奇异矩阵T，T满足如下Sylvester方程：

TΦ-FT=GΓ

令Ψ=ΓT-1，则系统(7)能够浸入如下系统：

如果σ是已知常量，文献[7-10]指出基于调节量反馈值设计的控制器能够解决系统的鲁棒输出调节问题。如果σ是时变或不确定参数，则需要通过自适应方法[2-3]或者其他工具[4,11-12]来处理。本文处理σ是已知常量的输出调节问题，σ是位置常量的问题留在将来的工作中解决。

2.2 控制律设计

雷达横摇轴系位置伺服系统跟踪误差为

e(t)=θc(t)+x1(t)

令ydis=θc(t)，将式(1)写成如下形式：

(8)

式中，a22=Fbkk/J，a23=Ktk/J，a31=KVPKVIKPAdd，a32=KVPKVIk-KVPFbkkk/J，a33=KVPKtkk/J，b3=KVPKVI，c34=J/(kKt)。综合外部系统式(2)和被控对象式(8)解形如式(6)的调节方程组得

(9)

式(9)为被控对象式(8)在外部干扰作用下保持系统补偿误差为0的不变流形。

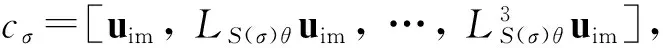
LS(σ)θcσ=Φcσ，uim=Γcσ

(10)

式中，Φ的特征根均是单根，且在虚轴上。

(11)

(12)

代入系统参数，容易验证式(12)在原点的平衡点是渐近稳定的。

定义χ=z3+a0z1+a1z2，其中a0和a1满足多项式P(λ)=λ2+a1λ+a0是Hurwitz的，则系统(12)转换为

(13)

当σ(t)已知时，存在内模控制器：

(14)

(15)

式(15)前两个方程构成系统(15)的零动态系统。令χ=0，由于多项式P(λ)=λ2+a1λ+a0是Hurwitz的，所以零动态系统在原点的平衡点是渐近稳定的。将z=[z1,z2]T看作零动态系统的状态变量，将χ看作输入，则零动态系统是ISS(Input-to-State Steady)的。已经证明，令H=-KG可消除H的影响[13]。综上所述，可得如下定理：

定理2[13]：针对被控对象式(1)，假设外部系统式(2)的参数σ(t)是已知的，用e(i)，i=1，…，r-1表示动态跟踪误差e的i阶导数，r为被控系统的相对阶。存在正实数K*，当K>K*时，内模控制器能够解决本文研究的输出调节问题。

(16)

式中r= 3。

3 仿真分析

3.1 系统参数

(1) 舰艇横摇角度满足式(2)，假设σ1(t)=0.9 rad/s，σ2(t)=1.6 rad/s，最大角速度0.16 rad/s，最大跟踪角加速度0.18 rad/s2。

(2) 按照σ1(t)=0.9 rad/s，σ2(t)=1.6 rad/s设计控制器参数并设计位置响应的带宽大于1 Hz。选取任意可控矩阵对(F,G)，这里取F具有负的特征值，分别为-3、-3、-3、-3，(F,G)如下：

计算得Ψ=ΓM-1=[78.93,108.0,50.63,12.0]，K是比例系数，取值K>0，设计a0和a1使得多项式P(λ)=λ2+a1λ+a0是Hurwitz的。综上所述，控制器的参数如表1所示，被控对象参数取值如表2所示。

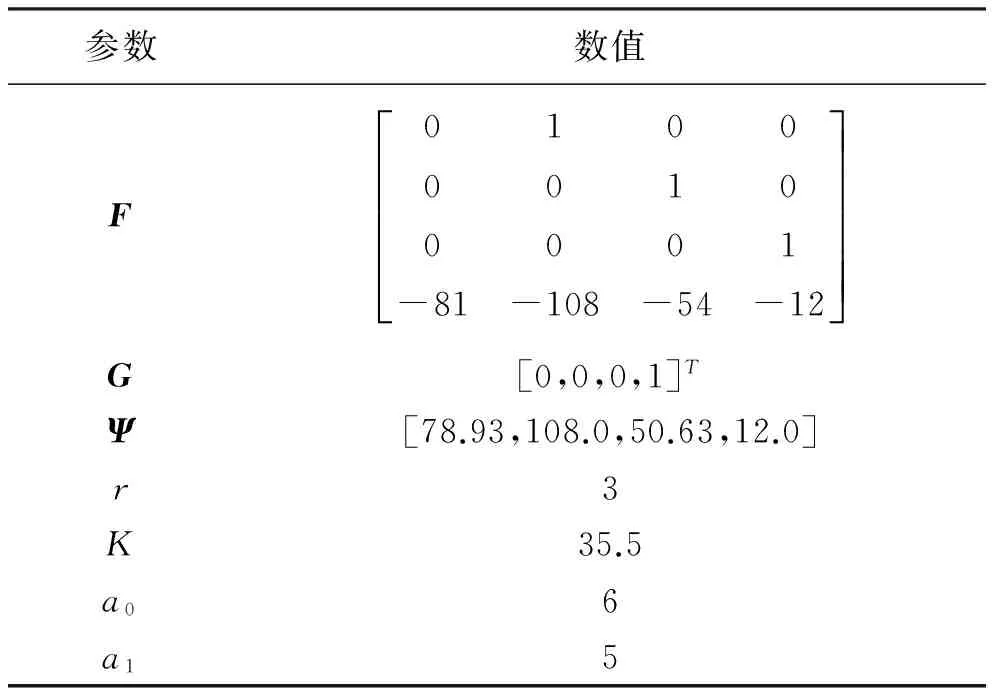
表1 内模控制器参数

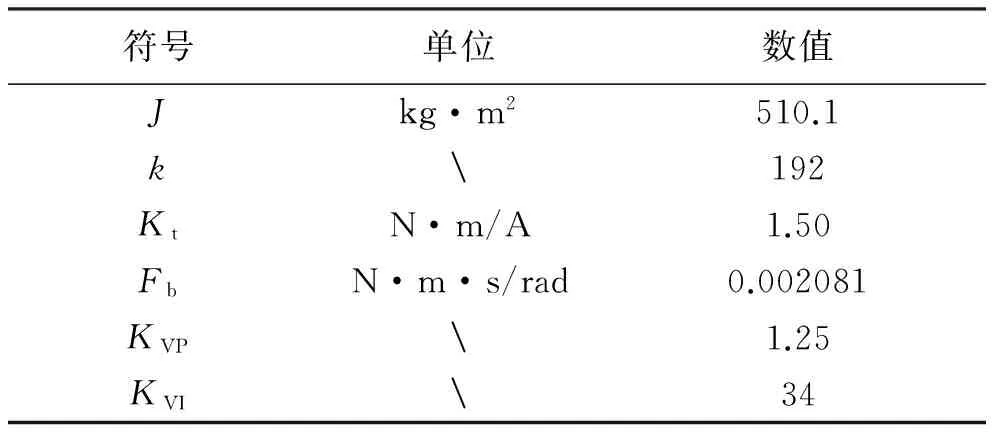
表2 被控对象参数

3.2 仿真结果与分析

进行了3种仿真：阶跃响应、补偿谐波信号和参数摄动仿真。仿真结果如图4～图5所示。图4是0.18 rad的阶跃响应曲线。图5是补偿谐波信号和参数摄动的仿真曲线，初始时刻存在0.33 rad的位置误差。由图4可知，系统在原点是稳定的，阶跃响应以指数规律收敛至零点。由图5可知，控制器能很好地补偿舰艇摇摆运动的干扰，系统补偿误差以指数规律收敛至零点，在t=14 s时将转动惯量增加0.5倍，系统补偿误差出现0.006 rad波动后仍以指数规律收敛至零点，可见控制器对系统转动惯量变化具有鲁棒性。仿真结果表明了本文设计控制律的有效性。

图4 阶跃响应曲线

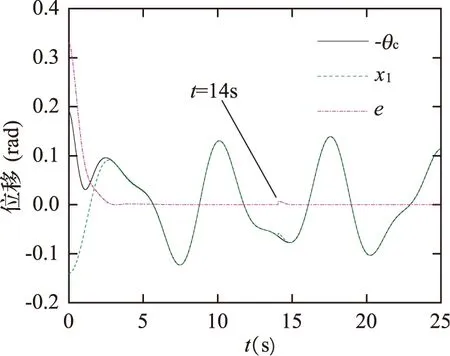
图5 补偿谐波信号和参数摄动仿真曲线

4 结束语

针对舰艇摇摆运动对雷达稳定平台系统控制响应性能的影响，研究了其基于内模原理的补偿控制问题。

(1) 建立了舰体甲板和雷达稳定平台控制系统数学模型，根据实际工作条件对数学模型中舰体耦合干扰项进行简化，使其变为线性项，方便后续理论分析和控制律设计。

(2) 针对一类已知频率信息的摇摆运动信号，设计了基于内模原理的控制律并证明了该方法的有效性，系统补偿误差是渐近收敛至原点的。

(3) 仿真结果显示，所设计控制器在原点具有指数稳定性。系统补偿误差以指数收敛至0，表明本文设计的内模控制律能很好地抑制舰体甲板运动对雷达稳定平台位置伺服系统的耦合干扰影响，且对系统转动惯量的变化具有鲁棒性。

[1] Nikiforov V O. Adaptive nonlinear tracking with complete compensation of unknown disturbances[J]. Euro. J. Control. 1998, 44:132-139.

[2] Serrani A, Isidori A, Marconi L. Semiglobal Nonlinear Output Regulation With Adaptive Internal Model[J]. IEEE Transactions on Automatic Control, 2001, 46(8): 1178-1194.

[3] Delli Priscoli F, Marconi L, Isidori A. A new approach to adaptive nonlinear regulation[J]. SIAM. J. Control Optimization, 2006, 45(3): 829-855.

[4] Marconi L, Praly L, Isidori A. Output Stabilization via Nonlinear Luenberger Observers[J]. SIAM Journal on Control and Optimization. 2007, 45(6): 2277-2298.

[5] Marconi L, Isidori A, Serrani A. Autonomous vertical landing on an oscillating platform: and internal-model based approach[J]. Automatica, 2002( 38): 21-32.

[6] Messineo S, Serrani A. Offshore crane control based on adaptive external models[J]. Automatica,2009(45): 600-605.

[7] Marconi L, Isidori A. A Unifying Approach to the Design of Nonlinear Output Regulators[J]. Adv. in Control Theory and Applications,2007, LNCIS 353: 185-200.

[8] Marconi L, Praly L. Uniform Practical Nonlinear Output Regulation[J]. IEEE Transactions on Automatic Control, 2008, 53(5): 1184-1202.

[9] Huang J, Zhiyong Chen. A General Framework for Tackling the Output Regulation Problem[J]. IEEE Transactions on Automatic Control, 2004, 49(12): 2203-2218.

[10] Byrnes C I, Delli Priscoli F, Isidori A, Kang W. Structurally Stable Output Regulation of Nonlinear Systems[J]. Automatica,1997, 33(3): 369-385.

[11] Wonhee Kim, Hyungjong Kim, Chung Choo Chung, etc.. Adaptive Output Regulation for the Rejection of a Periodic Disturbance With an Unknown Frequency[J]. IEEE TRANSACTIOINS ON CONTROL SYSTEMS TECHNOLOGY, 2011, 19(5): 1296-1310.

[12] Delli Priscoli F, Marconi L, Isidori A. Adaptive observers as nonlinear internal model[J]. SYSTEMS & CONTROL LETTERS, 2006, 55: 640-649.

[13] 庄文许. 基于内模原理的某舰载火箭炮操瞄系统控制研究[D]. 南京: 南京理工大学, 2013.

Research on stabilizing platform control of shipborne radars based on internal model principle

ZHUANG Wen-xu, ZHANG Yi, WENG Jian-guang

(No.724 Research Institute of CSIC, Nanjing 211153)

The stabilizing platform of the shipborne radar includes two degrees of freedom, which are used to compensate the pitch and roll angles of the ship respectively, and overcome the inertia moment caused by ship swing at the same time. Besides, load inertia varies with antenna rotation. The ship swing can be considered as overlapping of some sine signals, and the control law based on the internal model principle is designed for the ship swing with known frequencies. The simulation results indicate that the control law, which is robust to the amplitude, phase, and load inertia of the ship swing, performs well in the compensation of coupling disturbances of the ship. The steady-state tracking error is exponentially convergent to zero.

shipborne radar; stabilizing platform; internal model principle; robust

2014-05-05；

2014-07-11

庄文许(1985-)，男，工程师，博士，研究方向：结构设计与机电系统仿真；张毅 (1977-)，男，高级工程师，硕士，研究方向：结构设计与仿真分析；翁健光(1987-)，男，助理工程师，硕士，研究方向：结构设计与仿真分析。

TN959.72

A

1009-0401(2014)03-0043-05