一种二维数字阵列雷达的和差波束测角方法

杨蓓蓓

(中国电子科技集团公司第三十八研究所，合肥 230088)

一种二维数字阵列雷达的和差波束测角方法

杨蓓蓓

(中国电子科技集团公司第三十八研究所，合肥 230088)

研究了基于窗函数的二维数字阵列雷达和差波束测角方法。该方法在较大幅相噪声条件下能保证测角误差信号基本不变，且使用和波束与差波束共轭乘积虚部的正负号来确定目标角度相对于主波束的偏向，简化了确定目标偏向的计算过程，给出了数字阵列雷达中数字和差波束测角的详细过程。计算机仿真和实测结果表明，该方法具有良好的测角性能，适合于工程实际应用。

数字阵列雷达；和差测角；数字波束形成

0 引 言

传统的单脉冲测角是雷达的一项成熟技术。它通过利用一种特殊的天线馈电使得只需要一个单脉冲就可以产生4个波束，并通过天线或射频前端的混合器形成和波束、方位差波束和俯仰差波束[1]。对于二维数字阵列雷达，天线单元多达数千个，不能采用微波网络形成单脉冲和、差波束，只能通过数字信号处理形成和、差波束，因此称之为数字和差测角。本文根据基本单脉冲测角的思想，考虑到数字阵列雷达在数字信号处理及数字波束形成上的优势，给出了一种基于窗函数的二维数字阵列雷达和差波束测角方法，并给出计算机仿真结果，分析其性能，最后给出实测结果。

1 二维数字阵列雷达及其数字波束形成过程

随着数字技术的发展，雷达接收信号可以通过A/D转换器转换成数字信号，所以移相不一定需要专门的移相器，而可以通过数字方法实现移相。数字技术不但使移相方法可变，也使天线方向图可以用数字方式形成，称为数字波束形成技术[2]。实现数字波束形成的关键器件是数字阵列模块(digital array module，DAM)，每个DAM都包括相互独立的直接数字合成器(direct digital synthesizer，DDS)、功放、收发开关、A/D变换及中频正交采样等模块。数字接收波束形成时，数字接收机将各路天线阵元经收发开关、滤波后的信号直接进行A/D变换、数字正交采样得到I、Q信号，便可通过后端计算机用数字方法产生各种数字接收波束。数字发射波束形成时，通过控制各个DAM中DDS的初始相位，实现发射波束在两维空间的扫描[3-4]。

图1为垂直放置的M行N列的二维数字阵列雷达天线的坐标系示意图，X轴为阵列的法线，YOZ平面为雷达阵面所在平面。将阵面中心设置在坐标系原点O处，则阵列从左至右每列阵元的Y坐标为

(1)

从下至上每行阵元的Z坐标为

(2)

所有阵元的X坐标均为0，其中dz和dy分别为阵列垂直维和水平维的阵元间距。

图1 数字阵列天线坐标示意图

(3)

由此可得阵列的导向矩阵为

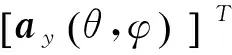
(4)

式中

式(5)、式(6)分别为行天线和列天线的方向矢量，其中k=2π/λ为波数，λ为波长。在数字波束形成过程中，整个阵列的加权矩阵为

(7)

式中，wz和wy分别为控制俯仰维和方位维副瓣电平的窗函数矢量，⊙表示点积。

2 基于窗函数的数字和差测角方法

天线设计中，和分布一般采用Taylor分布，差分布主要采用Bayliss分布。Bayliss分布是一种典型的差分布。它让阵列左右或上下两边单元的相位互相反相形成方位或俯仰差波束，同时降低差波束的副瓣电平[5]。因此，工程实现时采用Taylor和Bayliss窗函数形成和、差波束。根据式(7)和波束、方位差和俯仰差波束的加权矩阵可分别表示为

(8)

(9)

(10)

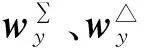
Taylor和分布由式(11)决定：

(11)

式中1≤i≤K，且

(12)

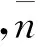
Bayliss差分布由式(13)决定：

(13)

式中1≤i≤K，且

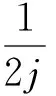
(14)

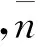
多项式系数见表1。

表1 多项式系数表

图2给出了阵元数为32、等副瓣电平个数为8、副瓣电平为-30 dB的归一化Taylor窗函数和Bayliss窗函数。

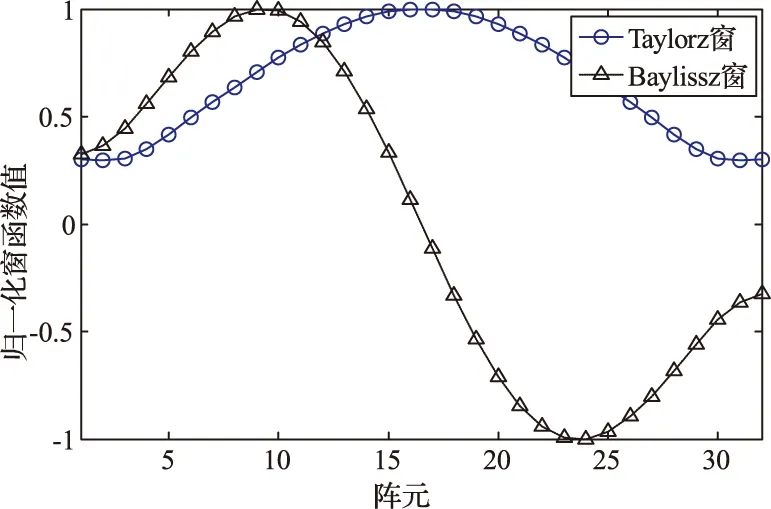
图2 归一化Taylor、Bayliss窗函数

假设坐标原点的平面波信号用解析信号表示为x(o,t)=s(t)ejω0t，则该平面波在天线阵面任一阵元r处的回波信号为x(r,t)=s(t+τ)ejω0(t+τ)，在窄带信号条件下有s(t+τ)≈s(t)，则DBF输出的和波束、方位差和俯仰差波束信号及其相位分别为

x∑(θ,φ;t)=s(t)ejω0t·sum[W∑(θ,φ)⊙A(θ,φ)]

(15)

(16)

(17)

Pha∑(θ,φ;t)=angle[x∑(θ,φ;t)]

(18)

(19)

(20)

式中sum[·]表示对括号内所有元素求和，angle[·]表示对括号内的元素求相位。

方位和俯仰测角误差信号为

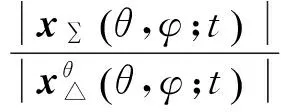
(21)

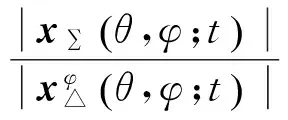
(22)

图3(a)为20行32列的阵列在dz和dy为半工作波长，方位维加入等副瓣电平个数8、副瓣电平-30 dB，俯仰维加入等副瓣电平个数6、副瓣电平-25 dB的Taylor权和Bayliss权，波束指向θ等于-40°、φ等于-15°时的归一化方位和差波束。图3(b)为不加权时相应的归一化方位和差波束。

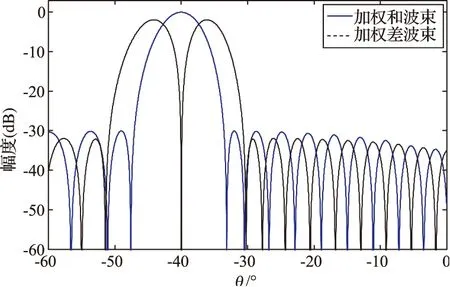
图3(a) 归一化加权方位和、差波束

图3(b) 归一化不加权方位和、差波束

由图3可知，加权之后方位和差波束的副瓣电平降低到-30 dB，而不加权时副瓣电平只能达到-13 dB，低副瓣电平能降低从副瓣进入的杂波和干扰，提高接收信号的信杂比，从而提高雷达的测角精度。特别对于机载数字阵列雷达来说，由于波束一般是下视扫描的，地杂波较地面雷达强很多，天线的低副瓣设计更是必须的。

图4为由式(21)、式(22)确定的与图3相对应的方位测角误差信号。

图4 方位测角误差信号

由图4可知，无论是否加权，一个测角误差信号值都会对应两个角度值，因此需要和差波束的相位信息来确定误差信号对应的角度是在波束指向的左边还是右边。图5为由式(18)～式(20)确定的与图3相对应的方位和、差波束相位。

图5(a) 加权方位和、差波束相位

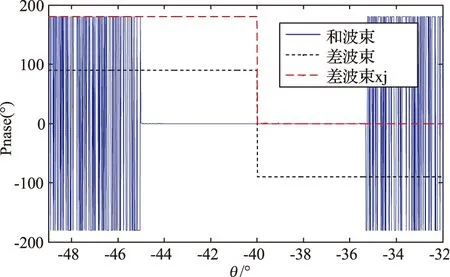
图5(b) 不加权方位和、差波束相位

由图5可知，方位主波束内和波束的相位为0°，差波束在波束指向左边和右边的相位分别为90°和-90°。将差波束的相位加上90°之后，在主波束内差波束在波束指向左边和右边的相位分别与和波束反相(相位相差180°)和同相(相位相差0°)。根据此相位差值就可以确定误差信号对应的角度是偏主波束指向的左边还是右边，从而确定最终的角度，完成和差测角。

图6为矢量A与B的矢量和、差的模值大小与其相位差值β的对应关系示意图。从图中可看出，当β为锐角时|A+B|大于|A-B|，当β为钝角时|A+B|小于|A-B|。

图6 矢量和、差模值大小与其相位差β对应关系

假设

x∑(θ,φ;t)=a+bj=A

(23)

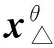
(24)

则有

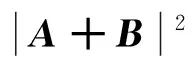
(25)

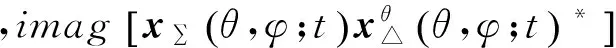
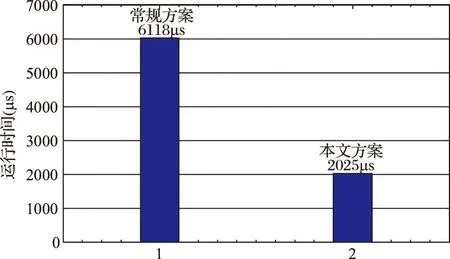
图7 常规方法和本文方法确定1000个点的角度偏向运行时间对比图

3 误差性能分析

影响和差测角性能的主要因素是空间环境和目标特性等带入信号的幅相误差及雷达自身硬件与相关算法代入信号的幅相误差[6-7]。以上两种误差可统一归结为雷达各通道之间的幅相误差。

图8给出了在阵面各个通道接收信号幅度中加入信噪比为0 dB的高斯白噪声，相位加入±20°的均匀分布噪声时，方位测角误差信号、方位差波束×j与和波束相位差与不加入噪声时理论值的对比图，仿真时所用的其它参数与图3所用参数一致。从图中可以看出，本文所述的二维数字阵列和差测角方法能在较大幅相噪声的条件下保证测角误差信号保持基本不变，且用来判断角度偏向的相位差信号基本不会偏离理论值太多，在主波束左边仍然保证差波束×j与和波束矢量夹角为钝角，在主波束右边为锐角。

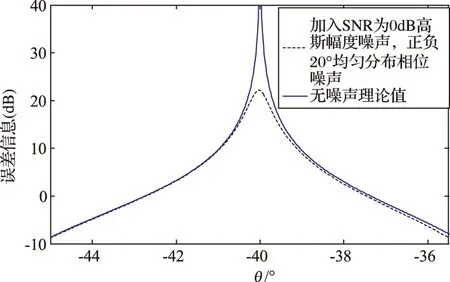
图8(a) 有无噪声加权方位测角误差信号对比图

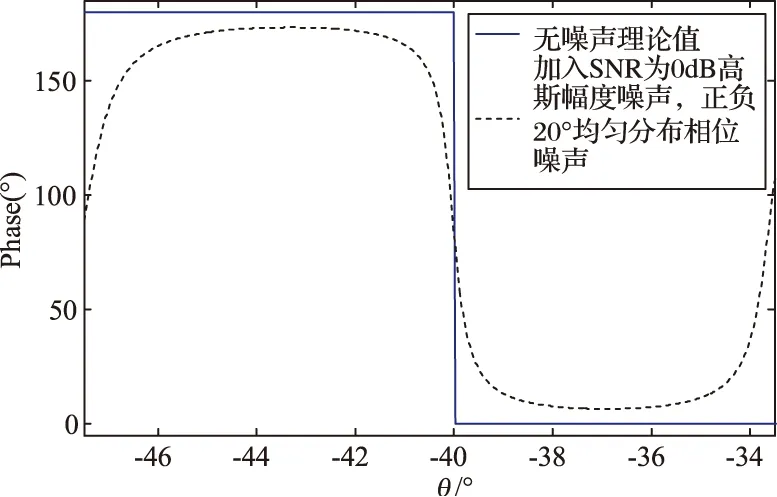
图8(b) 加权条件下有无噪声方位差波束×j与和波束相位差对比图

4 实际测试结果

图9为某数字阵列雷达采用本文所述和差测角方法得到的目标方位和俯仰的实际测角误差。以目标机GPS数据计算出的目标方位角和俯仰角为真值，经计算，该目标的方位角和俯仰角测量均方根误差分别为0.19°和0.43°。俯仰维测角误差较大是由于俯仰维的阵面有效孔径较方位维小，且俯仰波束受地面多径效应影响比方位波束严重。

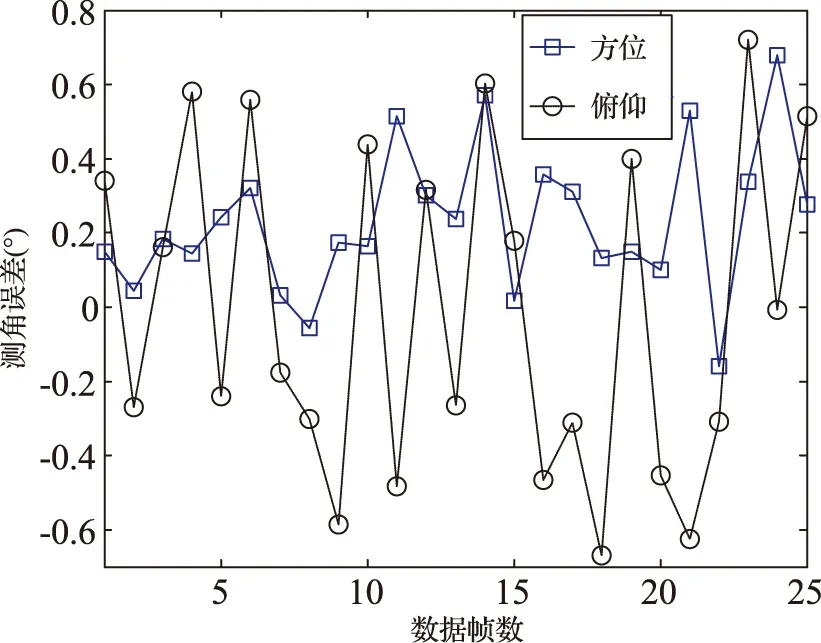
图9 某目标方位和俯仰的实际测角误差

5 结束语

本文详细阐述了一种基于窗函数的二维数字阵列雷达和差波束测角方法。该方法在较大幅相噪声的条件下能保证测角误差信号基本不变，且使用和波束与差波束共轭乘积虚部的正负号来确定目标角度相对于主波束指向的偏向，简化了确定目标偏向的计算过程，提高了计算效率，便于实际工程实现。计算机仿真和实测结果表明本文方法的有效性。

[1] Merrill I S.Radar handbook[M].New Yor-k:McGrawHill,1990.

[2] 吴顺君，梅晓春等.雷达信号处理和数据处理技术[M].北京：电子工业出版社，2008.

[3] 朱庆明.数字阵列雷达述评[J].雷达科学与技术，2004，2(3):136-141.

[4] 何明友.数字阵列雷达和软件化雷达[M].北京：电子工业出版社，2008.

[5] Robert J M.Phased array antenna handbook[M].London:Artech House,2005.

[6] Richard O N.Accuracy of angle estimation with monopulse processing using two beams[J].IEEE Trans.on Aerospace and Electronic Systems,2001,37(4):1419-1423.

[7] Zhen W,Abhijit S,Peter W,et al.Angle estimation for two unresolved targets with monopulse radar[J].IEEE Trans. on Aerospace and Electronic Systems,2004,40(3):998-1019.

An angle measuring method using sum and difference beams for 2D digital array radars

YANG Bei-bei

(No. 38 Research Institute of CETC, Hefei 230088)

An angle measuring method based on the window function using sum and difference beams for 2D digital array radars is studied. The error signal of angle measurement is basically unchanged under the condition of large amplitude and phase noise, and the positive and negative signs of the imaginary part of the product of the sum beam and the conjugate of the difference beam are used to determine the target deviation relative to the main beam angle, which simplifies the calculation process of determining the target deviation. The detailed process of the angle measuring method using digital sum and difference beams in digital array radars is given. The simulation and test results show that the method has a good performance in angle measurement and it is suitable for actual engineering applications.

digital array radar; sum and difference angle measurement; DBF

2014-04-26；

2014-06-23

杨蓓蓓(1982-)，女，工程师，硕士，研究方向：雷达信号处理和数据处理。

TN953.5

A

1009-0401(2014)03-0006-05