某舰载雷达发射机机柜抗冲击仿真分析

孟庆鹏，庄文许，顾郑强

(1. 海军驻南京地区雷达系统军事代表室, 南京 210003；2. 中国船舶重工集团公司第七二四研究所，南京 211153)

某舰载雷达发射机机柜抗冲击仿真分析

孟庆鹏1，庄文许2，顾郑强2

(1. 海军驻南京地区雷达系统军事代表室, 南京 210003；2. 中国船舶重工集团公司第七二四研究所，南京 211153)

针对某舰载雷达发射机机柜抗冲击设计要求，进行了机柜的抗冲击仿真分析。利用动力学分析方法，在抗冲击仿真软件中建立了机柜的仿真模型，在显式动力学分析步中将冲击谱时域曲线直接作用于机柜上的连接部位，并根据减振系统的实验数据计算得到发射机机柜在垂向、横向和纵向设计冲击谱作用下的冲击响应。结果显示，最大应力均不超过材料抗拉强度的90%，满足强度设计指标，为后续抗冲击试验提供了理论依据。

抗冲击；雷达系统；机柜；减振系统

0 引 言

相对舰艇有一定距离的水下非接触爆炸作用将引起舰艇突发的瞬态相对运动，该运动对舰艇而言就是冲击载荷。冲击载荷对舰总体、设备和船员的作用，是关键的破坏因素之一，需要在舰船研制时予以全面考虑并对设备进行良好的防护[1]。目前，主要有3种抗冲击设计方法：等效静力、动态设计分析法和时域模拟法。

时域模拟法考虑各种非线性因素的影响，可以较真实地反映系统的动力学特征，应用广泛。汪玉等对一类船舶设备的限位器进行抗冲击刚度计算，并运用带间隙的弹簧单元逼近限位器的冲击刚度，实现了非线性系统冲击响应模拟[2]；林道福等在总体坐标系下建立了浮筏隔振系统的运动方程，并采用直接积分法计算了在基础冲击激励下的动力响应[3]。

发射机是舰载雷达系统的重要件，在冲击载荷作用下，受到自身重量和安装在其内部组件重量产生的惯性力，产生冲击响应和变形。本文采用时域模拟法[4]对某舰载雷达系统发射机机柜进行抗冲击仿真计算。首先，在抗冲击仿真软件中建立机柜的仿真模型，将内部组件简化为质点耦合到相应的安装部位，然后将冲击载荷时域冲击谱作用于发射机机柜与减振系统的连接部位获得机柜的冲击响应和应力，最后依据减振系统的试验数据估计机柜实际工况下的应力分布。计算结果表明所设计的机柜在冲击载荷作用下是安全的，为产品的抗冲击试验、验收等程序提供依据。

1 问题描述

如图1所示，舰载雷达发射机机柜通过减振系统安装在舰艇甲板上，底部通过4个减振器与舰艇甲板连接，背面通过2个减振器与舰艇舱壁连接，冲击载荷即通过这6个减振器传递至发射机机柜上。

本文的任务是依据隔离系统的设计冲击时域曲线，计算骨架的应力分布、连接作用力等，校核骨架的强度。

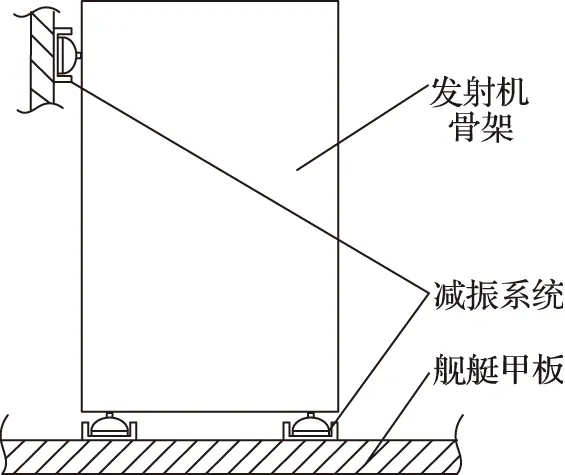
图1 发射机机柜安装示意图

2 问题求解

2.1 计算原理

冲击过程中，减振器的刚度和阻尼是非线性和时变的[5]，其参数难以准确获得，增加了仿真的复杂度，甚至与实际隔离系统相差太大以至于仿真结果没有参考意义。因此，本文采用数值计算和实验经验相结合的方法来校核机柜的强度。首先计算刚性连接情况下的冲击响应和应力分布，然后根据减振系统的实验经验，采用折算系数来估计应力分布，进而校核机柜的强度。

显式动力学适合于分析物体受冲击载荷并在结构内部发生复杂相互作用的瞬态响应问题。冲击问题即是此类问题。在整个运算过程中采用中心差分算法求解平衡方程，运用动态方程在每个微小的增量步内的动力学条件计算下一个增量步的动力学条件。

在动力学有限元分析中，系统的求解方程式为[6]

(1)

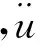
对于单个节点，阻尼矩阵和刚度矩阵为零，所以单个节点平衡方程转化为

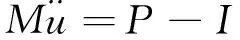
(2)

在当前增量步的t时刻，计算加速度为

(P-I)|(t)

(3)

在计算速度的变化时假设加速度是一个常量，应用这个速度的变化值加上前一个增量步中点的速度来确定当前增量步中点的速度。采用中心差分方法对加速度在时间上进行积分并可得到速度和加速度方程：

(4)

(5)

由此可见，利用显式动力学求解复杂的非线性问题时不必联立方程组进行求解，每一个增量步的计算成本很低，有效地提高了计算效率。

2.2 约束条件

在抗冲击仿真分析软件中建立发射机机柜的仿真模型，如图2(a)所示。将内部安装组件处理为质心，并耦合到相应的安装部位。在发射机骨架底部和背面连接减振器的部位分别建立参考点，并耦合至对应的连接部位。图2(b)是骨架底部连接部位的耦合参考点，图2(c)是骨架背部连接部位的耦合参考点，各耦合参考点如图中RP-i(i=2, …, 7)所示。

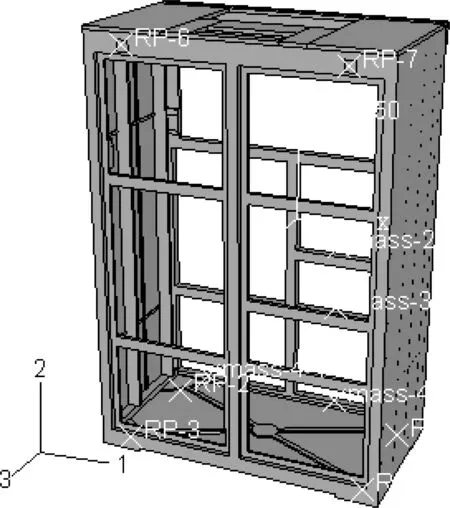
(a) 发射机机柜模型

(b) 底部约束和耦合参考点

2.3 驱动输入

按照设计要求，安装区域的设计冲击谱如表1所示。该加速度可以用双三角形时域曲线表示[8]，如图3所示，计算公式如式(6)所示。

(6)

式中，A0、V0和D0为该系统设计冲击谱中的等加速度谱、等速度谱和等位移谱。计算得3个方向时域冲击曲线的参数如表2所示。

表1 安装区域隔离系统设计冲击谱

图3 双三角形时域曲线

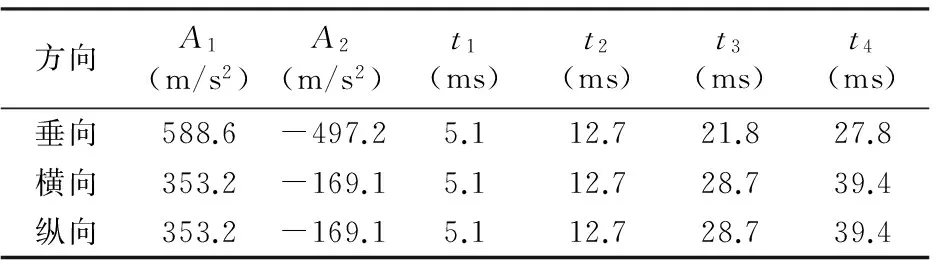
表2 安装区域减振系统设计冲击时域曲线参数

本文采用显式动力学方法。将该加速度时域曲线直接作用于各连接部位的耦合参考点上，计算获得所需要的结果。

3 计算结果与分析

计算获得机柜分别在3个方向冲击载荷作用下的应力分布时变过程，取冲击过程中3个方向应力最大时刻的结果，如图4～6所示。结果显示，刚性连接时，发射机机柜在受到垂向、横向和纵向冲击载荷时最大应力分别为241.5、189.6和146.8 MPa。

所选用材料抗拉强度为σb=231 MPa，根据抗冲击试验大纲，冲击作用下应力应小于所选材料抗拉强度的90%，即208 MPa。使用减振器后，在相同的工况下，骨架的应力将降低。不同减振器对应力的折算系数不同，考虑可靠性，选择折算系数小于0.8的减振器。

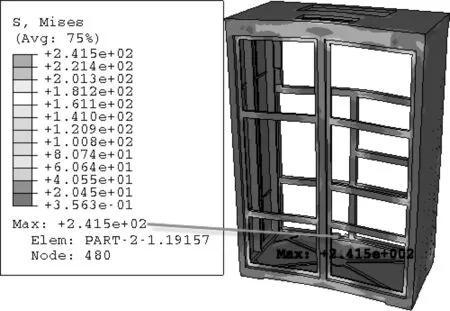
图4 t=34 ms垂向冲击应力响应云图

图5 t=28 ms横向冲击应力响应云图

图6 t=27 ms纵向冲击应力响应云图

4 结束语

针对舰载雷达系统抗冲击性能设计要求，对某系统发射机机柜进行了抗冲击仿真分析。

(1) 利用显式动力学分析步，分别计算了发射机机柜不使用减振器的工况下在垂向、横向和纵向冲击载荷作用下的冲击响应和应力分布。

(2) 不使用减振器工况下，发射机机柜在受到垂向、横向和纵向冲击载荷时最大应力分别为241.5、189.6和146.8。根据抗冲击大纲要求并考虑可靠性，选择折算系数小于0.8的减振器。

(3) 理论分析的结果为后续试验和产品验收等工作提供了参考。在后续的抗冲击试验中该发射机机柜没有出现破坏情况，表明理论分析结果具有重要的参考价值。

[1] 汪玉, 华宏星. 舰船现代冲击理论及应用[M]. 北京: 科学出版社, 2005.

[2] 汪玉，胡刚义，华宏星，等.带限位器的船舶设备非线性冲击响应分析[J]. 中国造船， 2003, 44(2): 39-44.

[3] 林道福,与永丰,华宏星.带限位器的浮筏隔振系统的冲击响应分析[J].噪声与振动控制,2004,46(1):36-43.

[4] 张影.船用齿轮箱抗冲击计算方法分析[D].哈尔滨工程大学,2010.3.

[5] 冯麟涵,汪玉,张磊.舰船设备抗冲击能力的可靠性分析[J].振动与冲击,2013,32(1):140-144.

[6] 庄茁，由小川，廖剑晖，等.基于ABAQUS的有限元分析和应用[M].北京：清华大学出版社，2009：190-191.

[7] 郝贵祥，王红岩，洪煌杰.空降车着陆缓冲过程仿真研究[J].机械科学与技术，2012，31(2)：340-344.

[8] 姜涛,王伟力,黄雪峰,等.舰艇抗冲击设计中正负三角波冲击谱分析与应用[J].海军航空工程学院学报,2010,25(2):145-148.

Research on anti-shock simulation of transmitter cabinet of a shipborne radar

MENG Qing-peng1, ZHUANG Wen-xu2, GU Zheng-qiang2

(1.Military Representatives Office for Radar System of the PLA Navy in Nanjing, Nanjing 210003; 2. No.724 Research Institute of CSIC, Nanjing 211153)

An anti-shock simulation of the transmitter cabinet of a shipborne radar is analyzed according to the anti-shock design requirements. The simulation model is built through the anti-shock simulation software and the dynamic analysis method. The shock spectrum time-domain curve is directly applied on the connecting parts of the cabinet in the explicit dynamic analysis steps. According to the test data of the shock absorber system, the shock responses of the cabinet under shock spectrums from vertical and horizontal orientations are obtained. The simulation result indicates that the maximum stress is less than 90% of the tensile strength of the materials, which satisfies the strength index and provides a theoretical basis for the following anti-shock tests.

anti-shock; radar system; cabinet; shock absorber system

2014-05-13；

2014-05-20

孟庆鹏(1983-)，男，工程师，研究方向：雷达总体技术；庄文许(1985-)，男，工程师，博士，研究方向：结构设计与机电系统仿真；顾郑强(1981- )，男，工程师，硕士，研究方向：结构耐振与抗冲击设计。

TN957.82

A

1009-0401(2014)03-0039-04