利用运动特性消除多目标时差定位模糊
2014-09-08王向敏
臧 勤,王向敏,田 利
(中国船舶重工集团公司第七二四研究所,南京211153)
利用运动特性消除多目标时差定位模糊
臧 勤,王向敏,田 利
(中国船舶重工集团公司第七二四研究所,南京211153)
时差定位系统由于方程多解、高重频等原因造成的定位模糊问题一直是关注的热点。从工程应用出发,提出了一种利用运动目标特性消除多目标时差定位模糊的方法。该方法在不增加设备成本的基础上在航迹起始的过程中排除虚假定位点,有效地消除了目标定位模糊。
时差;无源定位;定位模糊;高重频
0 引 言
无源定位设备自身不发射信号,通过对目标上的电磁信号的搜索测量和处理得到目标的位置及参数信息,因此具有良好的隐蔽性。
时差定位系统通过三站布站,获取两组时间差进行辐射源定位,取二次曲线的交点作为辐射源的位置进行求解。时差定位精度高,数据率高,定位速度快,但同时由于时差误差大、平方求解多根、高重频等原因存在定位模糊的问题。
某些定位模糊可以根据先验知识和布站排除一些[1],但实际应用中的布站受到地域特征的限制有很多局限性,无法避免地存在定位模糊现象。在多个文献中也提出了通过时差和测向结合消除定位模糊,但这种方法需要增加新设备,增加系统成本。在实际应用中,更希望通过在不增加硬件成本的情况下解决定位模糊的问题。
本文主要通过在对定位目标进行航迹起始的过程中,依据点迹相关性,目标运动特性,排除错误的定位结果,同时形成正确的起始航迹。
1 时差定位算法
目前定位计算有多种方法,如Chan算法、Tayler算法、FANG算法、SX算法、 Sl算法、 DAC算法等。通过仿真,本文采用Chan算法——一种计算简单的非递归算法。该算法计算量小,精度高,易于工程实现。以三站二维布站、辐站夹角为120(240)°为例,其求解步骤如下:
设待定的辐射源位置为M(x,y),它到主站A(x0,y0)和从站B(xi,yi)的距离差为△Ri(i=1,2),则时差定位方程为
△Ri=c·△ti,i=1,2
直接将二维算法写成矩阵形式如下:
AX=B
式中
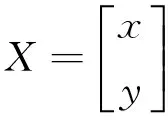
其中

其中

△Ri=c·△ti,i=1,2
假设三站布站夹角120(240)°,即r(A)=2,可用伪逆法解方程AX=B得到辐射源位置的估计值:
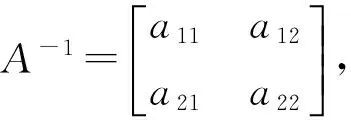
写成方程形式:
其中
将上式代入表达式,得到
其中
解方程可得到R0的解。最后,把R0带入,得到辐射源位置的值(x,y)。
2 定位模糊问题
由上节可知,在定位求解过程中,有一个求解二次方程式的过程,其结果会得到2个根。若2个根都为实根,则会产生定位模糊问题。用双曲线示意图表示,如图1所示。

图1 两条双曲线的交点为2个实根
在二维平面内,目标信号到达两测量站的时间差确定了一对以两站为焦点的双曲线。如果利用三个站则形成两条双曲线,两对双曲线可能有两个交点。这就产生了定位的模糊性, 有时甚至得不到合理的解[2]。
针对定位模糊的问题,很多文献都对此进行过研究,大致总结有以下几种方法:
(1) 通过反代入时差方程的方法去除模糊[3],即分别用得到的2个实根代入计算,用误差最小原则去除增根。但是,这种方法判断错误的概率约超过10%,很可能得到错误的定位结果。
(2) 借助某站测得的目标辐射源方位角,消除定位模糊[4]:将2个实根反代入计算,得到2个定位点分别计算方位,在门限范围内的为真实定位点。该方法正确性较高,但需要额外的设备投入,在设备有限的情况下无法实现。
(3) 对于定位的实时性要求不太高的目标可以采取多次定位法消除定位模糊,即对目标辐射源进行多次定位解算,通过比对多次的定位结果,很容易判断出来,从而消除定位模糊[5]。
本文在该方法的基础上作了改进,根据运动目标的特性,通过少量次数的定位解算,消除定位模糊。
3 依据目标运动特性消除定位模糊
假设三站布站如上文所设,中心站为中心点,两辅站分别位于中心点左右两侧,三点用“+”表示。每隔一段距离设置一个目标点用“*”表示,通过反推计算时间差,根据时间差画出两组双曲线,如图2所示。深色双曲线是主站和左辅站的时间差曲线图,浅色双曲线是主站和右辅站的时间差曲线图。
根据图2很容易发现,只有某些区域会出现双解问题。因此,运动目标在运动过程中会经历从单解到双解或从双解到单解的变化过程。
若航迹起始初期不在双解区域内则在目标跟踪后期,只要根据之前得到的航迹信息就可以排除虚假点;若航迹起始初期在双解范围内,暂时记录双解进行同时航迹起始,当目标运动到非双解区域即可以排除虚假点;若航迹一直处于双解区域,则根据历史数据进行相关,依据目标运动特性把不合理的航迹作为虚假航迹进行排除。只要顺利找到了正确的航迹,通过相关性就能轻松排除后期的定位模糊。
4 消除定位模糊方法的实际应用
针对一般目标进行定位时,本周期定位结果和下一个周期的定位结果需要进行关联。假设前一组定位结果有2个,后一组定位结果也有2个,首先需要对2*2组数据对进行计算匹配,只有距离差在门限内的数据对认为有关联。第一组解中的解1与第二组解的2个解进行距离计算,得到d11、d12。第一组解中的解2与第二组解的2个解进行距离计算,得到d21、d22。
在一般目标情况下,每次定位只要对2个解进行关联即可,如图3所示。
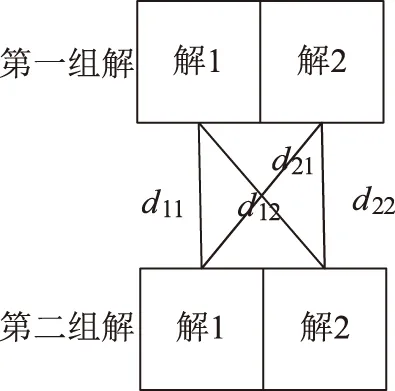
图3 一般目标双解定位结果关联
因此,每个周期定位结果与前一个周期定位结果进行关联时,只需要计算4次,进行比较即可。
记录第一组解对应的所有可能关联。找不到门限范围内的关联解则直接删除,找到一组解关联的可以唯一确定,存在多组解关联则通过与其他组的对应关系进行比较排除,找到最合理的关联关系。
在门限范围内的解留下来,其他删除。当解1存在两个对应关系d12、d13,解2存在一个对应关系d23,解1排除掉d13,只取d12。依次类推,每收到该目标相应的定位信息时就进行一次排除,直到只有一个解,形成一条目标航迹为止。
但是,在实际应用中,除了双解问题外,还会遇到高重频问题。即
detaT=△t+n*PRI,
detaT 其中,L为两个站之间基线长度,△t=t2-t1,detaT为高重频所有可能时间差。 如果脉冲重复频率过高,即脉冲重复间隔PRI较小时,就会出现n>1的情况。 当高重频遇到双解问题时,每个目标每次定位将会有n*2个解。按照一般目标的处理思路,需要对2n*2n组数据对进行计算匹配。以第一组解中的解1为例,与第二组解的2*n个解进行距离计算,得到d11,d12,d13,…,d12n。第一组解中的2*n个解需要与第二组解的2*n个解进行距离计算,得到2n*2n个距离,只有距离差在门限范围内的数据组认为有关联,见图4。 根据高重频目标定位特征,高重频的每个解都能形成一个航迹。根据参考文献[6],由于目标与接收机之间存在相对运动,基于径向的微量偏移进行排除。 计算每组点迹的径向偏移量: △R=|dis(D1-P2)-dis(D2-P2)| 图4 高重频目标定位结果关联 其中,D1为点迹1的直角坐标系值,P2为主站的直角坐标系值,D2为点迹2的直角坐标系值。而△R-△RealR≤Thr,△|RealR=C×|△t,Thr为门限,根据经验取一个固定值,△t=t2-t1,以光速为极限速度,取距离门限值Thr=C×△t。 但是,在等待一条目标航迹的过程中还是需要对每个周期的定位结果不停地进行计算、关联,这在实际应用中需要花费过多的时间,影响定位效率。 图5 高重频目标时差定位航迹 如图5所示,根据高重频目标的每个解都能形成一个航迹的特征可以推出,每条航迹上每个定位点的时间差detaT是比较接近的。因此,可以推出,当△t为最小正值时,每条航迹上获取每个定位点时间差的n值是一样的。 因此,在应用中,当计算出△t时需要添加一步操作,即获取最小△t,以确保n可以作为索引,直接通过n对每个周期的高重频数据进行关联,对每个时间差只需要像一般目标一样计算双解结果的关联即可。这大大减少了计算量,提高了定位效率。 在工程应用中都是对多个目标同时进行定位,因此在消除定位模糊的过程中还需要对多个目标进行各自关联,寻找正确的多个目标航迹。在目标个数较多的情况下,计算量过大。因此在整个时差定位系统的设计过程中,通过信号分选引导调度,进而操控天线的方法实现对多个目标的同时定位。 同时在复杂的电磁环境下即使通过上述算法进行排除,依旧会产生较多的虚假航迹,给后续的跟踪带来一定影响。因此,在后续的工作中还需要进一步考虑回波等复杂情况,根据每种信号的特性排除虚假点。 [1] 韩丽君.平面三站时差定位中的模糊研究[J].计箅机与数字工程,2012(5):10-11. [2] 王玲,魏星,万建伟,刘云辉.基于TDOA定位算法的模糊解消除方法[J].计算机工程与科学,2006,28(3):74-75. [3] 谢恺,钟丹星,邓新蒲,等.一种空间时差定位的新算法[J].信号处理,2006,22(2):129-135. [4] 任文娟,胡东辉,丁赤飚,牛彝.利用测向信息消除高重复频率信号的时差定位模糊[J].电子与信息学报,2010,32(12). [5] 曾辉,曾芳玲.空间三站时差定位的模糊及无解问题[J].信息与电子工程,2010,48(2). [6] 陆洪涛,马飞.基于多普勒频率差的三站无源定位技术[J].舰船电子对抗,2008,31(1):29-31. A way of using movement characteristics to eliminate multi-target time-difference locating ambiguity ZANG Qin, WANG Xiang-min, TIAN Li (No. 724 Research Institute of CSIC, Nanjing 211153) The locating ambiguity caused by the multiple solutions of the equation and the high pulse repetition frequency is always a concern for the time-difference locating system. A new method of eliminating multi-target time-difference locating ambiguity through the target movement characteristics is proposed from engineering applications. This method can remove false locating points in the process of the track initiation and effectively eliminate the target locating ambiguity without the cost of equipment increased. time difference; passive location; locating ambiguity; high pulse repetition frequency 2014-06-12; 2014-08-12 臧勤(1983-),女,工程师,硕士,研究方向:雷达终端显示与数据处理;王向敏(1980-),女,工程师,硕士,研究方向:雷达终端显示;田利(1978-),男,工程师, 研究方向:雷达系统总体技术。 TN953.7 A 1009-0401(2014)03-0020-03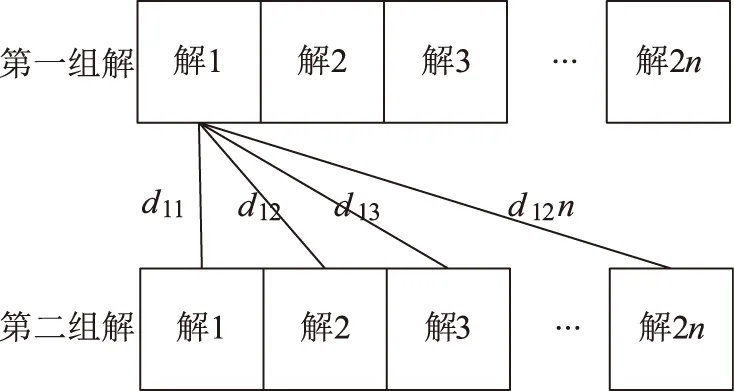

5 结束语
