带有不完全信息随机截尾试验下伽玛分布尺度参数的点估计

何朝兵, 刘华文

(1.安阳师范学院 数学与统计学院, 河南 安阳 455000; 2.山东大学 数学学院, 济南 250100)



带有不完全信息随机截尾试验下伽玛分布尺度参数的点估计

何朝兵1*, 刘华文2

(1.安阳师范学院 数学与统计学院, 河南 安阳 455000; 2.山东大学 数学学院, 济南 250100)

首先通过添加数据得到了带有不完全信息随机截尾试验下伽玛分布的完全数据似然函数,然后分别利用EM算法和MCMC方法对尺度参数进行了估计,最后进行了随机模拟试验,结果表明尺度参数点估计的精度比较高.

完全数据似然函数; EM算法; 满条件分布; MCMC方法; Gibbs抽样

伽玛分布是一类应用广泛的连续型分布,尤其在水文、气象、海洋和可靠性领域,并且伽玛分布与泊松分布、威布尔分布、卡方分布等分布都有着密切的关系.关于伽玛分布的研究可参看文献[1-6].近些年来,关于随机截尾试验的研究比较多,带有不完全信息随机截尾试验(random censoring test model with incomplete information),简称IIRCT,由文献[7]首次研究,接着文献[8-18]深入研究了IIRCT下寿命分布的参数估计,但对IIRCT下伽玛分布的参数估计,却很少有文献进行研究.本文通过添加数据得到了IIRCT下伽玛分布的完全数据似然函数,给出了由EM算法得到的参数的迭代公式,接着利用MCMC方法得到了参数的Gibbs样本,把Gibbs样本的均值作为参数的贝叶斯估计,进行了随机模拟试验,结果表明参数的EM估计和MCMC估计的精度都较高.

1带有不完全信息随机截尾试验(IIRCT)

设X1,X2,…是独立同分布的非负随机变量序列,其分布函数为F(x;θ)=P(Xi≤x),密度函数为f(x;θ),θ是未知参数.又设Y1,Y2,…是独立的非负随机变量序列,分布函数分别为G1(y),G2(y),…，密度函数分别为g1(y),g2(y),…且gi(y)与参数θ无关.{Xi}与{Yi}独立.

为估计参数θ,n个样品的观察数据{Zi,1≤i≤n}如下:

1) 当Xi≤Yi时,有两种情况:Xi以概率ai立即显示,此时取Zi=Xi;Xi以概率1-ai不被显示,此时取Zi=Yi.称ai为失效显示概率.

2) 当Xi>Yi时,取Zi=Yi.

引入随机变量αi,βi,i=1,2,…,n.

若Xi≤Yi,αi=1;若Xi>Yi,αi=0.

Xi≤Yi,且未被显示时,βi=0;其它情况,βi=1.

综上所述,有

P(βi=1|αi=1)=ai,

P(βi=0|αi=1)=1-ai.

设Zi的观察值为zi,则基于数据{(zi,αi,βi),1≤i≤n}的似然函数为：

[g(zi)F(zi;θ)(1-ai)]αi(1-βi)·

(1)

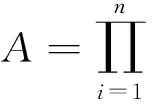
2IIRCT下伽玛分布参数的点估计

2.1完全数据似然函数

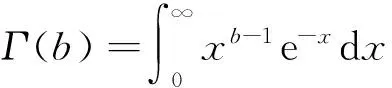
假设IIRCT下产品寿命Xi～Ga(b,θ),且形状参数b已知,下面对尺度参数θ进行估计.

由(1)式可以看出,伽玛分布基于截尾数据的似然函数比较复杂,为了方便进行参数估计,下面添加缺损的Xi的值,以获得完全数据的似然函数.具体如下:

当αi=1,βi=0,即第i个产品失效未被显示时,添加数据Z1i=Xi=z1i.

在Xi≤zi的条件下,Z1i的条件密度函数为:

它是区间(0,zi]上的截断伽玛分布Ga(b,θ),其样本可表示为：

z1i=F-1{F(0)+U0[F(zi)-F(0)]}=F-1{U0F(zi)},

其中，F是Ga(b,θ)的分布函数,F-1为其反函数,U0为来自均匀分布U(0,1)的一个随机样本.

当αi=0,即Xi>Yi时,添加数据Z2i=Xi=z2i.

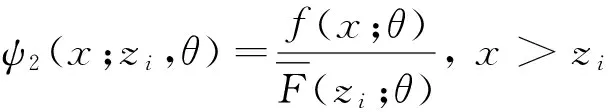
Z2i也服从截断伽玛分布,其样本的获得与Z1i类似.

令α表示αi组成的向量,β表示βi组成的向量,z表示zi组成的向量,u表示z1i组成的向量,v表示z2i组成的向量,则完全数据似然函数为：

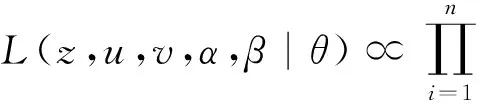
[f(z1i;θ)]αi(1-βi)[f(z2i;θ)]1-αi}=

2.2EM算法

EM算法是一种迭代方法,并主要用来求后验分布的众数,即极大似然估计,它的每一次迭代由两步组成:E步(求期望)和M步(极大化).EM算法非常适合处理不完全数据,下面利用EM算法来求θ的MLE.

取θ的先验分布为伽玛分布Ga(c,d),c,d已知,即

π(θ)∝θc-1e-dθ,θ>0,c>0,d>0.

则θ的添加后验分布为：

L(θ|z,u,v,α,β)∝π(θ)L(z,u,v,α,β|θ)∝

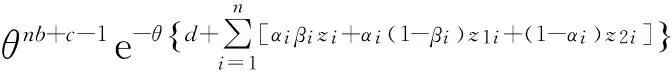
在第m+1次迭代中,假设有估计值θ(m),则可通过E步和M步得到θ的一个新的估计.

令U表示Z1i组成的向量,V表示Z2i组成的向量.

为了书写方便,简记(|θ(m)，z，α,β)为(|·).

E步:

当αi=1,βi=0时,

当αi=0时,

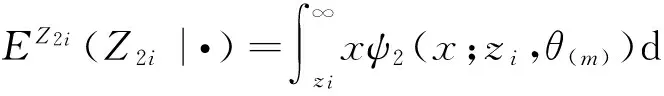
而要获得Z1i,Z2i期望的显式表示是不可能的,这时可用Monte Carlo方法完成,这就是所谓的Monte Carlo EM(MCEM)方法,它将E步改为:

(E1) 利用逆变换法随机产生li个随机数k1,k2,…,kli.利用逆变换法随机产生ri个随机数s1,s2,…,sri;

(E2) 计算

(2)

M步:

得

θ(m+1)=

(3)

(3)式给出了由EM算法得到的形状参数θ的迭代公式.

由上述讨论可知,EM算法只适用于nb+c-1>0的情况.

2.3参数的贝叶斯估计

当αi=1,βi=0时,

π(z1i|θ,z,z-1i,v,α,β)∝ψ1(z1i;zi,θ),

其中,z-1i={z1j:j≠i}.

当αi=0时,

π(z2i|θ,z,u,z-2i,α,β)∝ψ2(z2i;zi,θ),

其中,z-2i={z2j:j≠i}.

参数θ的满条件分布为:

π(θ|b,z,u,v,α,β)∝

(4)

由于得到了各参数的满条件分布,下面利用MCMC方法获得参数θ后验分布的平稳分布.z1i,z2i的满条件分布都是截断伽玛分布,可以利用逆变换法随机抽样;θ的满条件分布是伽玛分布,是一个标准分布,所以这3个分布都可以采用Gibbs抽样.

设θj,j=1,2,…,M1,…,M2为参数θ的一个容量为M2的Gibbs样本,其中M1为由于不稳定而舍弃的样本容量,然后利用达到平稳状态的M2-M1个独立样本的均值作为参数θ的贝叶斯估计,即

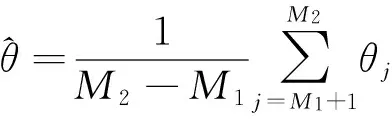
(5)

EM算法得到的估计是后验分布的众数(MLE),MCMC方法得到的估计是后验分布的期望,由于θ的满条件分布是伽玛分布,并且满条件分布抽样依分布收敛到后验分布,所以为了讨论EM估计和MCMC估计的关系,下面先讨论一下伽玛分布的众数和期望的关系.

若X～Ga(λ1,λ2),则E(X)=λ1/λ2.当0<λ1≤1时,X的密度函数严格下降,众数不存在;当λ1>1时,X的密度函数是单峰函数,众数为(λ1-1)/λ2,此时众数比期望小,但当λ2较大时两者的差别较小.

3随机模拟

基于上面的讨论,下面进行随机模拟试验.设Xi服从伽玛分布Ga(11,θ),θ=9,取参数θ的先验分布为伽玛分布Ga(5.2,0.6);截尾变量Yi～Ga(13,8),失效显示概率a=0.8,样本容量分别取n=30,50,100,200,300,500,800,1000.对每一固定样本量随机产生一组不完全随机截尾数据,然后根据此组数据分别利用EM算法和MCMC方法对参数θ进行估计.

运用EM算法时从θ=16开始迭代;运用MCMC方法时,从θ=12.5开始进行Gibbs抽样,MCMC模拟运行过程中,先进行10000次Gibbs预迭代,以确保参数的收敛性,然后丢弃最初的预迭代,再进行10000次Gibbs迭代,把第10001次至第20000次的迭代值的算术平均值作为λ的估计值. EM估计和MCMC估计的R程序运行结果参见表1.

表1 IIRCT下伽玛分布参数估计的随机模拟结果Tab.1 Random simulation results of parameter estimation of gamma distribution for IIRCT

当n=300时,EM算法迭代10次,Gibbs迭代20000次,迭代过程参见图1和图2.

图1 n=300时,参数θ的EM迭代过程Fig.1 EM iterations of θ with n=300

图2 n=300时,参数θ的Gibbs抽样迭代过程Fig.2 Gibbs sampling iterations of θ with n=300

由表1可以看出,θ的EM 估计和MCMC估计的差别不大,与真值9的相对误差都小于7%,MCMC估计比EM估计更接近真实参数θ;样本量对估计值的影响也不大,说明得到的估计值是比较稳定的,并且精度也较高.

注1 在编写R程序时用到的函数主要有:

gamma(), unif(), binom(), min(), max(), sum(), mean(), plot()等.

[1] Gupta S S. Order statistics from the gamma distribution[J]. Technometrics, 1960, 2(2): 243-262.

[2] Choi S C, Wette R. Maximum likelihood estimation of the parameters of the gamma distribution and their bias[J]. Technometrics, 1969, 11(4): 683-690.

[3] Wilks D S. Maximum likelihood estimation for the gamma distribution using data containing zeros[J]. Journal of Climate, 1990, 3(12): 1495-1501.

[4] Khodabin M, Ahmadabadi A. Some properties of generalized gamma distribution[J]. J Math Sci, 2010, 4: 9-28.

[5] Huang W, Shu L, Jiang W, et al. Evaluation of run-length distribution for CUSUM charts under gamma distributions[J]. IIE Transactions, 2013, 45(9): 981-994.

[6] Alam A, Rahman M S, Saadat A H M, et al. Gamma distribution and its application of spatially monitoring meteorological drought in barind, bangladesh[J]. Journal of Environmental Science and Natural Resources, 2013, 5(2): 287-293.

[7] Elperin T I, Gertsbakh I B. Estimation in a random censoring model with incomplete information: exponential lifetime distribution[J]. IEEE Transactions on Reliability, 1988, 37(2): 223-229.

[8] Elperin T, Gertsbakh I. Bayes credibility estimation of an exponential parameter for random censoring and incomplete information[J]. IEEE Transactions on Reliability, 1990, 39(2): 204-208.

[9] Ye E. Consistency of MLE of the parameter of exponential lifetime distribution for random censoring model with incomplete information[J]. Applied Mathematics, 1995, 10(4): 379-386.

[10] 陈怡南, 叶尔骅. IIRCT下对数正态和正态分布参数的MLE[J].南京航空航天大学学报:自然科学版, 1996,28(3):376-383.

[11] 陈怡南, 叶尔骅. 带有不完全信息随机截尾试验下Weibull分布参数的MLE[J].数理统计与应用概率, 1996, 11(4):353-363.

[12] 杨纪龙, 叶尔骅. 带有不完全信息随机截尾试验下Weibull分布参数的MLE的相合性及渐近正态性[J].应用概率统计, 2000, 16(1):9-19.

[13] 张晓琴, 张虎明. 带有不完全信息随机截尾试验下Weibull分布参数的MLE的重对数律[J]. 应用概率统计,2002,18(1):101-107.

[14] 宋毅君, 李补喜. 带有不完全信息随机截尾试验下最大似然估计的相合性及渐近正态性[J].应用概率统计, 2003, 19(2):139-149.

[15] 宋毅君, 李补喜, 李济洪. 带有不完全信息随机截尾试验下最大似然估计的重对数律[J]. 应用概率统计, 2009, 25(2):113-125.

[16] 宋凤丽, 沈 思. 带有不完全信息随机截尾试验下总体均值型参数的经验似然[J].应用数学, 2009, 22(1):191-198.

[17] 刘有新, 戴 扬. 带有不完全信息随机截尾数据的Fisher信息阵[J].重庆工商大学学报:自然科学版, 2008, 25(6):569-572.

[18] 何朝兵. 带有不完全信息随机截尾试验下几何分布的参数估计[J].应用数学, 2013, 26(3):574-579.

Point estimation of scale parameter of Gamma distribution for random censoring test model with incomplete information

HE Chaobing1, LIU Huawen2

(1.School of Mathematics and Statistics, Anyang Normal University, Anyang, Henan 455000;2.School of Mathematics, Shandong University, Jinan 250100)

In this paper we firstly obtain the complete data likelihood function of gamma distribution for IIRCT after adding data， then estimate the scale parameter by EM algorithm and MCMC method， respectively. Finally random simulation tests are conducted， and the results show that the point estimations of the scale parameter are fairly accurate．

complete data likelihood function; EM algorithm; full conditional distribution; MCMC method; Gibbs sampling

2014-01-13.

国家自然科学基金项目(61174099); 河南省教育厅自然科学基金项目(2011B110001).

1000-1190(2014)04-0479-04

O213.2; O212.8

A

*E-mail: chaobing5@163.com.