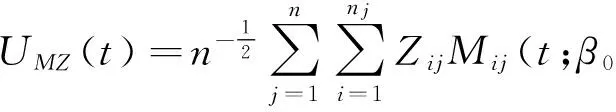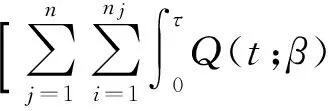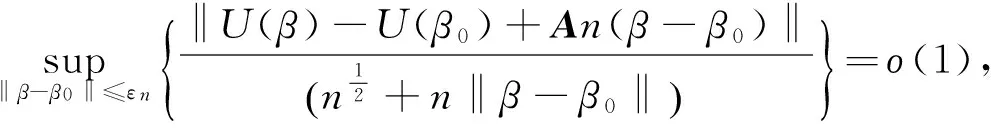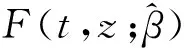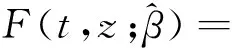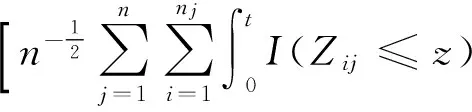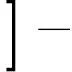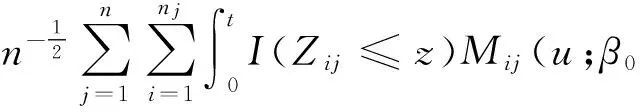成组复发事件下的加速失效时间模型

王 芬, 何 穗

(1.湖北第二师范学院 数学与统计学院, 武汉 430205;



成组复发事件下的加速失效时间模型

王 芬1*, 何 穗2

(1.湖北第二师范学院 数学与统计学院, 武汉 430205;

2.华中师范大学 数学与统计学学院, 武汉 430079)

对成组复发事件数据建立了半参数加速失效时间模型,在这个模型中协变量对均值函数在整个复发过程中有加速、减速的作用.该文利用估计方程的理论,给出了该模型中未知参数和基本比率函数的估计,同时利用现代经验过程理论证明了所得估计的相合性和渐近正态性.

加速失效时间模型; 成组复发事件; 估计方程

在许多研究背景下,对每个个体而言,某种感兴趣的事件会反复多次发生,这类情况的事件称为复发事件(Recurrent Event).复发事件数据就是对一些个体进行观察,某种感兴趣事件重复发生的时间所组成的数据,这类数据经常出现在生物,医学,社会和经济学等研究领域中.另外,在一些生物医学的学习中,研究的个体之间的经历可能是相关的,这样的数据又是成组数据.例如,在家庭或多区域的研究中,来自于同一家庭或同一区域的个体之间可能是相关联的.如果在研究中感兴趣的事件是成组数据,并且这些感兴趣的事件在观察的时间内可能多次发生,这样的数据称之为成组复发事件数据.在许多应用中,经常发生这样的情况:个体自身感兴趣的事件之间不相互独立,并且研究的个体之间也是不相互独立的.例如,对肾衰竭病人的住院治疗率的研究中,在同一地理区域的病人由于不可测量的病人特征可能是相关的[1-2].

在许多应用背景下,半参数加速失效时间模型已经得到了广泛应用,它是另一类重要的半参数模型.对于经典的生存数据,对Cox比率危险模型的一个重要替代就是加速失效时间模型,在此类模型中失效时间取对数后与协变量是线性关系,协变量的影响有加速、减速的作用.

对复发事件数据, 文献[3]提出了下面的加速失效时间模型:

通过一般化rank-type估计方程[4-6],估计了模型中回归参数的向量,并用现代经验过程理论,证明了估计参数的相合性和渐近正态性.

文献[7]提出了复发事件数据下的一类加速均值回归模型:

其中,β10和β20是p维的未知回归参数.该模型下,取β10=0,g(x)=ex时,该模型就是比率均值模型;当取g(x)=1时就是加速失效时间模型;当取g(x)=ex,β20=-β10时就是复发事件下的加速比率回归模型.

同样的,本文对成组复发事件数据,给出了相应的加速失效时间模型.

1模型和估计方法

首先给出本文需要用到的记号.对j=1,…,n,i=1,…，nj和k=1,2,…,令Tijk表示第j集族中第i个个体第k次事件发生的时间,其中,n表示集族数,nj表示第j集族中研究个体数.令

为t时刻第j集族中第i个人所经历的事件数,其中,当A成立时I(A)=1,否则I(A)=0.记第j集族中第i个人得右删失时间为Cij;令Zij(t)为p维协变量.由于删失时间的存在,研究个体所经历的事件可能有些不能被观察到,记可观察到的事件数为:

其中,a∧b=min(a,b).可观察到的数据集合为:

{Nij(·),Yij(·),Zij},

j=1,…,n;i=1,…,nj,

其中,Yij(s)=I(Cij>s).在给定协变量向量时,假定每个个体的删失时间条件独立于复发事件过程,也就是

而一个集族中个体之间的删失时间是没有必要相互独立的.

对成组复发事件数据,给出下面的加速失效时间模型:

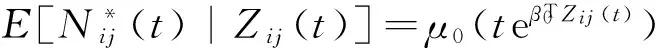
(1)

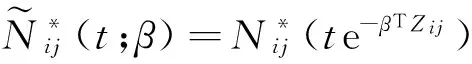
(2)

或

(3)

其中,误差项εij是同分布的.方程(3)式是非变量的加速失效时间模型.

令

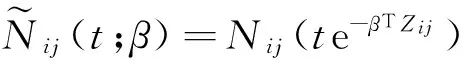
Yij(t;β)=I(Cij≥te-βTZij).

定义

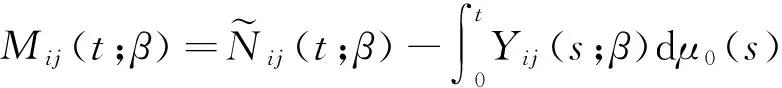
易知

故

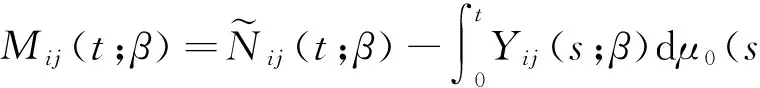
又由方程(2)知,Mij(t;β0)是均值为零的随机过程.因此,给定β,μ0(t)的合理估计值是下列方程的解,

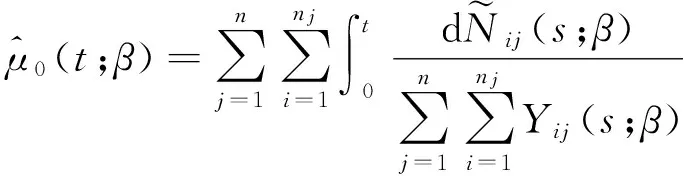
为了估计β0,由比例强度泊松过程模型[8]中的偏似然得分函数和模型(3)中的权重秩估计函数,提出β0的估计函数为:

其中,Q(t;β)是特定的权重函数,且

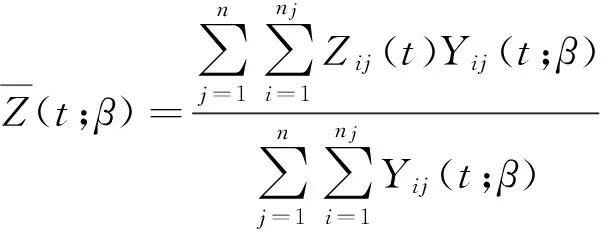
(4)

(5)

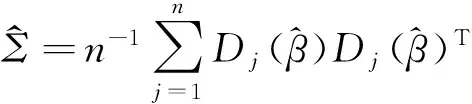
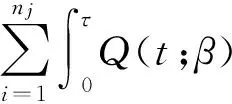
且

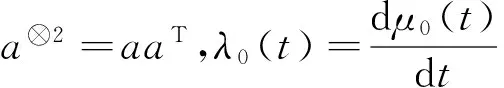
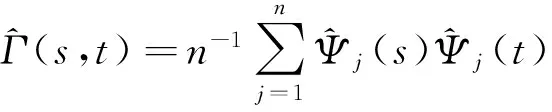
其中,

所以,与文献[9]一样,用V(t)的近似分布区推断μ0(t).

2拟合优度检验

和其他回归模型一样,模型(1)精确性的估计得拟合优度法是重要的. 与文献[13]类似,考虑下面残差和:

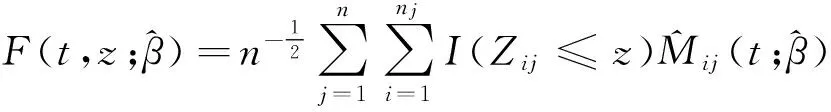
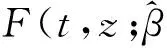
(6)

其中,

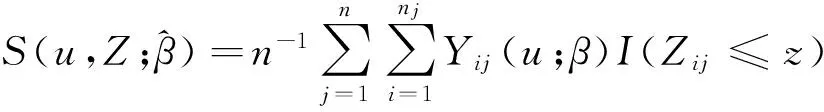
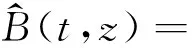
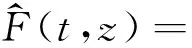
3渐近性质

现在来讨论模型(1)的函数估计值的渐近性质.首先,假定下列正则条件成立:

(C2)P(Yij(τ;β)=1)>0；

(C3)对j=1,…,n,i=1,…，nj,Nij(t)和Zij在[0,τ]上是有界的；

(C4)nj

(C5)Q有有界变差,并且几乎处处收敛到连续函数q；

(C6)Cij(β0)具有有界密度,且μ0(t)的二阶导数有界；

(C7)A是正定矩阵,其中,

证明主要采用文献[9]中的方法.首先,证明有限区间[0,τ]上的弱收敛性,其中,τ满足

令

定理2假设条件(C1)～(C7)成立,且对所有β∈N,除去β≠β0外,U(β)≠0,则有

1) 对任意εn→0,

=o(1)

(7)

几乎处处成立,其中,

证明

U(β)-U(β0)=

Yij(t;β)dμ0(te(β0-β)TZij)}-

(8)

μ0(te(β0-β)TZij)-μ0(t)=

故(8)右边的第二项为

o(n‖β-β0‖)=

-An(β-β0)+o(n‖β-β0‖)

几乎处处成立.将前面(8)右边的第一项和第二项的近似代入(8)式,可得对任意序列εn→0,

定理3在条件(C1)～(C7)下,V(t)弱收敛到均值为零的高斯过程,其在(s,t)处的协方差函数为Γ(s,t)=E{Ψj(s)Ψj(t)},其中,

证明为了得到V(t)的渐近正态性,首先注意到

由定理1的证明可知

在t∈[0,τ]上一致成立.又

在t∈[0,τ]上一致成立.由文献[9]中的定理1容易得到

因此

(9)

证明主要采用文献[7]中的证明方法.记

(10)

运用文献[6]和文献[9]中的证明方法,可以得到(10)右边的第一项对任意的t和z一致为ο(1).与(9)相似,(10)右边的第二项等价于

其中,

对(10)式的右边的第三项进行Taylor展开,它等价于

其中,

b*(t,z)=

所以,对任意t和z一致的有

[1] Schaubel D E, Cai J W. Analysis of clustered recurrent event data with application to hospitalization rates among renal failure patients[J]. Biostatistics, 2005,6:404-419.

[2] Schaubel D E, Cai J W. Semiparametric methods for clustered recurrent event data[J]. Lifetime Data Analysis, 2005,11:405-425.

[3] Lin D Y, Wei L J, Ying Z. Accelerated failure time models for counting processes[J]. Biometrika, 1998,85:609-618.

[4] Tsiatis A A. Estimating regression parameters using linear rank tests for censored data[J]. Ann Statist, 1990,18:354-372.

[5] Lai T L, Ying Z L. Estimating a distribution function with truncated and censored data[J]. Ann Statist,1991,19(1):417-442.

[6] Ying Z. A Large Sample Study Of Rank Estimation For Censored Regression Data[J]. Ann Statist, 1993,21:76-99.

[7] Sun L Q, Su B. A Class of accelerated means regression models for recurrent event data[J]. Lifetime Data Analysis, 2008,14:357-375.

[8] Andersen P K, Gill R D. Cox’s regression model for counting processes: a large sample study [J]. Ann Statist, 1982, 10:1100-1120.

[9] Lin D Y, Wei L J, Ying Z. Accelerated failure time models for counting processes[J]. Biometrika, 1998,85:609-618.

[10] Chen Y Q, Jewell N P. On a general class of hazards regression models[J]. Biometrika, 2001,88:687-702.

[11] Lin D Y, Geyer C J. Computational methods for semiparametric linear regression with censored data[J]. J Comput Graph Statist,1992, 1(1):77-90.

[12] Parzen M I, Wei L J, Ying Z. A resampling method based on pivotal estimation functions[J]. Biometrika,1994, 81:341-350.

[13] Lin D Y, Wei L J, Yang I,et al. Semiparametric regression for the mean and rate function for of recurrent events[J]. J R Statist, Soc B, 2000,69:711-730.

[14] Pollard D. Empirical processes: theory and applications[M]. Hayward: Institute of Mathematical Statistics,1990.

[15] Bilias Y,Gu M, Ying Z. Towards a general asymptotic theory for cox model with staggered entry [J]. Ann Statist, 1997, 25:668-682.

[16] Schorack G R, Wellner J A. Empirical Processes with Applications to Statistics[M]. New York: Wilery,1986.

Accelerated failure time models for clustered recurrent event data

WANG Fen1, HE Sui2

(1.College of Mathematics and Statistics, Hubei University of Education, Wuhan 430205;2.School of Mathematics and Statistics, Huazhong Normal University, Wuhan 430079)

In this paper， we present a natural extension of accelerated failure time model for survival data to formulate the effects of covariates on the mean function of the counting process for Clustered Recurrent event data. Making use of the theory of estimating equation， the unknown parameter in the model is estimated. Based on modern empirical process theory， the consistency and asymptotic normality of the proposed estimators are proved．

accelerated failure time models; clustered recurrent event; estimating equation

2013-11-21.

国家科技部国际合作重点专项基金项目(2010DFA31790);湖北省教育厅科学技术研究基金项目(B2014006).

1000-1190(2014)04-0468-06

O212.7

A

*E-mail: 55421810@qq.com.