基于最小二乘与粒子群算法的压力传感器动态补偿方法

轩春青,轩志伟,陈保立

(1.郑州成功财经学院信息工程系,河南 巩义 451200;2郑州大学信息工程系,郑州 450001; 3.中北大学电子测试技术国防重点实验室,太原 030051;4.武汉高德红外股份有限公司,武汉 430070)



基于最小二乘与粒子群算法的压力传感器动态补偿方法

轩春青1,2*,轩志伟3,4,陈保立3

(1.郑州成功财经学院信息工程系,河南 巩义 451200;2郑州大学信息工程系,郑州 450001; 3.中北大学电子测试技术国防重点实验室,太原 030051;4.武汉高德红外股份有限公司,武汉 430070)

为了降低运用简化传感器模型对动态测试结果进行修正时带来的误差,提出一种基于最小二乘(LSM)与粒子群优化算法(PSO)的动态补偿器设计方法。采用最小二乘法识别传感器的最佳阶次,作为补偿器的阶次,克服简化模型对补偿器设计的影响,结合粒子群算法对传感器进行逆建模得到补偿器,并分析补偿前后传感器的时域与频域特性。实验表明,该方法能有效的降低传感器的动态测量误差。

动态误差补偿;阶次识别;最小二乘与粒子群优化算法;频带拓展

爆炸冲击波是一个高速变化的过程,具有很宽的频谱,测压传感器应具有足够高的频率响应,以便可靠地反映压力的变化过程[1]。现有的传感器受制作工艺等条件的限制,工作频带窄于信号的频谱,动态性能不能满足测量的要求。在冲击波信号的激励下,传感器输出的信号将在谐振点处发生震荡,引入动态误差,无法准确判别出压力的真值。为了使测试结果更加精确,必须对传感器的动态特性进行补偿,提高传感器的响应速度、抑制超调量、扩展其频带范围以满足动态测量需要[2]。

采用数字滤波器对传感器输出进行动态补偿时,只需要辨识出滤波器的阶次和参数,具有补偿效果好,便于硬件实现等优点。常用的动态补偿方法有零极点方法、最小二乘法以及神经网络算法补偿等。使用零极点方法补偿时,需要确定传感器的数学模型,其物理实现难度较大;神经网络算法的全局搜索能力差、收敛速度慢,对滤波器参数进行最优求解时,易陷入局部极值[3-4]。PSO算法是一种全局最优算法,具有实现容易、精度高、收敛快等优点,但寻优结果受传感器阶次的影响较大。为此,本文提出一种基于最小二乘法判别传感器阶次模型与微粒群优化算法的压力传感器动态补偿方法。根据传感器对输入激励的响应,通过最小二乘法识别出最接近传感器模型的阶次作为动态补偿器的阶次。然后根据动态标定的激励和得到的响应通过粒子群优化算法求解出补偿器的参数。整个补偿过程简单,显著提高了传感器的动态响应特性。

1 传感器动态模型确定与补偿原理

1.1 压力传感器的动态模型

压力传感器一般等效为二阶系统,在数据处理中为了获取好的补偿效果,大多将传感器看做具有较高阶次的系统。但是阶次过高,会加大求解补偿器时计算的工作量而对补偿效果改善极小。因此需要对传感器的阶次做必要的验证,精确确定其模型结构。本文利用传感器在阶跃信号激励下的响应数据,根据最小二乘法通过残差的方差来判定系统阶次。

假设动态补偿环节满足如下模型

A(z-1)z(k)=B(z-1)u(k)+v(k)

(1)

(2)

其中n为模型阶次。

模型的最小二乘格式可写成

(3)

式中,数据向量和参数向量定义为

(4)

运用最小二乘原理,可获得模型参数θn的最小二乘估计为

(5)

式中,数据矩阵和输出向量定义为

其中,L为数据长度。模型阶次为n时,输出残差向量可写成

(6)

式中

(7)

残差的方差为

(8)

激波管产生的压力信号可以看成是阶跃信号,压力传感器的输出作为对阶跃信号的响应。为了辨识计算的方便,对传感器的输出进行了归一化处理。利用阶跃信号与传感器输出,采用残差方差的方法进行阶次辨识,得到的不同阶次估计时残差的方差的值如图2所示。

图1 某压力阶跃响应

图2 不同阶次残差的方差值

从图2可以看出,残差的方差在n=2时,显著下降,然后开始略微有些下降,由于系统的一些噪声以及传感器结构等,用一个高阶的系统来描述该压力传感器系统会更准确,构建相应阶次的补偿器对其传感器输出进行补偿时可以得到更好的补偿效果。但是补偿器阶数越高,其硬件实现难度越大,不易于嵌入到测试系统中。权衡补偿效果和滤波器的硬件实现的难度,文中补偿滤波器的阶次选为八阶。

1.2 传感器动态误差修正方法

图3 传感器动态误差修正原理图

目前对压力传感器动态补偿的方法是在其后串接一个补偿环节[2],该补偿环节的传递函数为压力传感器系统传递函数的逆函数。通过串接补偿环节扩展传感器的通频带,提高其响应速度等。图3给出了基于PSO算法的传感器动态误差修正的一般原理,其中y(k)为传感器输出,r(k)为参考模型输出,z(k)为补偿输出,m为补偿器的阶数[4]。通过对传感器经行动态标定获得其对阶跃信号的响应。以传感器的输出作为输入,阶跃信号作为输出,利用粒子群算法采用逆建模的方式,对补偿滤波器的参数进行辨识。使用获取的滤波器参数构造出补偿滤波器,并串联于传感器之后,使得等效的传感器系统满足不失真的测量条件[5],即可实现传感器动态误差的修正。

2 基于粒子群算法的压力传感器动态补偿器的设计

通常根据传感器系统受到的激励和输出响应来建立方程来求取动态补偿滤波器的参数。动态补偿滤波器参数的求解可等效为一个在2n维空间中的优化求解的问题,通过寻优得到全局最优解,本文选用粒子群算法进行求解。

2.1 粒子群算法原理

粒子群优化算法(PSO)具有高度的并行性、稳定性和全局搜索能力,比遗传算法更加简单、高效,很适合解决求最优解问题。基本思想是在解空间里初始化一群随机粒子,然后按照一定规则迭代,最终收敛找到最优解。在每一次迭代中,粒子通过跟踪个体极值最优解pbest和全局极值最优解gbest,利用下面两个公式来更新自己的速度和位置[6]。

V=wV+c1r(·)(pbest-p)+c2r(·)(gbest-p)

(9)

p=p+V

(10)

式中:V为粒子的速度;p为粒子的当前位置;pbest与gbest分别为个体极值和全局极值;c1,c2是学习因子;r(·)为(0,1)之间的随机数;w为加权因子。为了在搜索速度和搜索精度之间达到平衡,本文采用线性递减惯性权值策略[7-8](LDIW),w按照式(11)进行自更新;即在迭代的初期,w选取较大的值,以保证较快的搜索速度,在迭代后期选取较小的值,保证算法收敛达到一定的精度。

(11)

式中N为最大迭代次数,k为当前迭代次数。

本文适应度函数采用均方误差,定义如下:

(12)

动态补偿滤波器传递函数可以表示成如下形式:

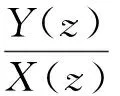
(13)

由于bi和ai成比例,故bi和ai可以归一化到一个以0为中心的对称的实数空间里,在该范围内能够找到系数的最优解。

2.2 动态补偿滤波器参数的辨识

由前面阶次识别可知,用一个八阶的线性系统来表示传感器系统,补偿器的参数为a=(a0,a1,a2,a3,a4,a5,a6,a7,a8);b=(b0,b1,b2,b3,b4,b5,b6,b7,b8)。为了获取传感器对激励信号的动态响应,必须对传感器进行动态标定。用于冲击波测试系统校准的激励源,其带宽至少要达到100 kHz。激波管作为“理想”阶跃压力函数发生器在压力传感器的动态校准中得到广泛应用。激波管可产生一个上升时间极短(10-8s～10-9s),并具有一定持续时间的阶跃压力,它的激励可以看作是一个阶跃压力信号。选用激波管对传感器进行激励,能充分获得传感器的动态特性,获取传感器的实际输出。由于传感器输出数据噪声很少,可以直接用做粒子群优化算法的输入,来辨识动态补偿滤波器的参数。

3 压力传感器的动态补偿结果

将压力传感器固定在激波管末端,进行动态标定试验。使用采集卡记录激励信号x(t)以及传感器的响应输出y(t)。图4所示是压力传感器受激波管激励后经归一化处理的响应数据。由图4可见,压力传感器在谐振频率处被充分激励起来,超调量超过100%,输出信号严重失真。

将激波管激励看成一个阶跃压力信号,可以直接以传感器的输出y(t)为输入,阶跃信号x(t)为输出,使用粒子群算法对补偿器进行参数识别,针对每个传感器进行多次寻优求解,并将获取的结果代入到系统中进行补偿,通过对补偿结果进行对比选取效果最好的补偿器,其参数为:

a=[-1.9889,-1.7778,-1.0057,-0.8320,0.5203,0.8155,0.7526,0.8635,0.6670];

b=[-0.6244,-0.4206,-0.0007,-0.2421,-0.5055,0.0980,-0.3741,-0.4330,0.5180];

可得到该补偿滤波器的传递函数为:

H(z)=(-0.6244-0.4206z-1-0.0007z-2-0.2421z-3-0.5055z-4+0.098z-5-0.3741z-6-0.433z-7+0.518z-8)/(-1.9889-1.7778z-1-1.0057z-2-0.832z-3+0.5203z-4+0.8155z-5+0.7526z-6+0.8635z-7+0.667z-8)

采用获取的动态补偿滤波器在计算机上对传感器的输出y(t)进行离线动态补偿,结果如图6所示,补偿后其上升时间为15 μs,超调量为3%,有效带宽由70 kHz扩展到300 kHz。接入补偿器后在一定程度上消除了传感器谐振频率的影响,有效频带得到扩展,动态特性明显改善,减小了测试的动态误差。根据获取的滤波器参数,可以在相应的微处理器中通过软件编程构建出相应的滤波器。将该滤波器固化到采集系统中,就能通过实现对获取数据的实时处理。

图5 压力传感器的幅频特性曲线

图6 激波管压力测试信号和补偿结果

理论上讲采用动态补偿技术可以任意展宽系统的工作频带。因为无限展宽频带会导致高频噪声放大,甚至淹没有用信号,使得测量无法进行。频带展宽范围为传感器带宽的2～10为佳[9]。由于补偿器扩展了测量系统的频带,使得传感器输出信号中的高频噪声,在经过补偿器后被加重,影响到测量精度,为此,可以采用低通滤波的方法消除高频噪声的干扰[10-12]。

4 结论

在压力传感器输出端串联一个动态补偿滤波器,可以有效的展宽传感器的频带,提高其动态响应速度,在一定程度上减小传感器的带宽较窄引起的测量误差,但一般动态补偿环节的方法都对传感器模型进行等效和简化,将其视为一个二阶系统,从而引入新的误差。

为了更好地对压力传感器动态特性进行补偿,本文提出一种基于最小二乘与粒子群优化算法相结合求解补偿滤波器的方法。首先,对传感器进行动态标定,获取其对阶跃输入信号的响应。利用传感器的输入输出使用最小二乘法对传感器阶次进行识别,考虑到补偿精度和硬件实现难易的问题,对补偿滤波器的阶数进行确定;然后使用阶跃输入和传感器对激励的响应进行逆建模,使用粒子群算法寻优求解,得到补偿器的参数。因能辨识出传感器的模型阶次,避免了简化建模带来的误差,补偿结果更加精准、动态特性得到很大提升。因补偿器的参数已知,硬件实现起来比较容易,精度更高。实验证明,该算法收敛性好、补偿精度高,且易于硬件实现。

[1] 张远平,池家春,龚晏,等. 爆炸冲击波压力测试技术及其复杂信号的处理方法[J]. 仪器仪表学报,2007,28(8):325-327.

[2]刘清,曹国华. 基于微粒群算法优化的微硅加速度传感器动态补偿研究[J]. 仪器仪表学报,2006,27(10):1707-1710.

[3]俞阿龙. 基于传神经网络的加速度传感器动态建模方法[J]. 仪器仪表学报,2006,27(3):325-327.

[4]吴健,张志杰,王文廉. 传感器动态误差高速并行修正方法及其FPGA实现术[J]. 传感技术学报,2012,25(1):67～71.

[5]孙海波,孔德仁,何瑛等. 传感器动态误差修正方法探讨[J]. 南京理工大学学报,2000,24(8):330-333.

[6]Fang Wei,Sun Jun,Xu Wenbo. A New Mutated Quantum-Behaved Particle Swarm Optimizer for Digital IIR Filter design[J]. EURASIP Journal on Advances in Signal Processing,2009,10(2):1-7.

[7]张媛媛,徐科军,许耀华. 改进PSO算法结合FLANN在传感器动态建模中的应用[J]. 振动与冲击,2009,28(1):1-4.

[8]陈贵敏,贾建援,韩琪. 粒子群优化算法的惯性权值递减策略研究[J]. 西安交通大学学报,2006,40(1):53-56.

[9]禹东川. 压力传感器动态性能分析与动态补偿[J]. 中国仪器仪表,2003(7):9-11.

[10]刘清,曹国华. 模型参考和误差白化的传感器动态补偿算法[J]. 控制理论与应用,2009(26):256-260.

[11]刘一江,孟立凡,张志杰. 基于遗传算法的传感器动态特性改善方法[J]. 传感技术学报,2013,26(9):1248-1253.

[12]刘一江,孟立凡,张志杰. 基于改进RLS的传感器动态特性校正方法[J]. 传感技术学报,2013,26(6):857-860.

轩春青(1982-),女,河南周口人,硕士,现任郑州成功财经学院讲师,主要从事数据采集、嵌入式系统设计等的研究,完成省部级课题4项,在国内刊物发表论文17篇,Zhangxuanchunqing@163.com;

轩志伟(1989-)男,河南周口人,硕士,主要从事动态测试与嵌入式系统等方面的研究,在国内刊物发表论文10篇,shine071201@163.com;

陈保立(1985-),男,汉族,硕士,主要从事动态测试与数字信号处理的研究。

DynamicCompensationMethodBasedonLeastSquaresAlgorithmandParticleSwarmOptimizationforPressureSensor

XUANChunqing1,2*,XUANZhiwei3,4,CHENBaoli3

(1.Department of Information Engineering,Zhengzhou Chenggong University of Finance and Economics,Gongyi He’nan 451200,China;2.Department of Information Engineering,Zhengzhou University,Zhengzhou 450001,China;3.National Key laboratory for Electronic Measurement Technology,North University of China,Taiyuan 030051,China;4.Wuhan Gold Infrared Co.,LTD,Wuhan 430070,China)

In order to correct the error caused by dynamic characteristics of sensor by using simplified model,a design method of dynamic compensator based on least square method(LSM)& particle swarm optimization(PSO)algorithm is presented. Using the least square method to identify the optimal order of the sensor,which used as the order of the compensator,an analysis about the dynamic characteristics of the sensor is made in the time domain and frequency domain. Experimental results show that this method can effectively reduce the dynamic measurement error of the sensor.

dynamic error compensation;order identification;least square method & PSO algorithm;band expansion

2014-05-10修改日期:2014-08-27

10.3969/j.issn.1004-1699.2014.10.011

TP212.6

:A

:1004-1699(2014)10-1363-05