一种用于磁流体陀螺微弱信号检测的小波降噪方法研究*

王丽萍,李醒飞*,吴腾飞,纪 越,徐梦洁,陈 诚

(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072;2.天津商业大学机械工程学院,天津 300134)



一种用于磁流体陀螺微弱信号检测的小波降噪方法研究*

王丽萍1,李醒飞1*,吴腾飞1,纪 越1,徐梦洁1,陈 诚2

(1.天津大学精密测试技术及仪器国家重点实验室,天津 300072;2.天津商业大学机械工程学院,天津 300134)

新型磁流体陀螺可以同时满足卫星微角颤振在轨测量的亚微弧度测量精度及千赫兹带宽的技术要求,优于当前卫星系统中所用陀螺,是用于卫星微角颤振测量的理想传感器。但是其输出信号极其微弱并且淹没在大量噪声中导致无法有效地实现检测角速度的功能。提出了一种基于自相关的小波阈值去噪算法提取微弱信号。该方法通过计算小波分解各层细节分量的自相关系数,自动确定最优小波分解层数,并通过该自相关系数选择最优去噪阈值。对传统阈值去噪算法与所提出的改进小波算法进行了对比实验,实验结果表明该方法能将输出信号信噪比提高7 dB～10 dB,适用于所设计的磁流体陀螺微弱信号的检测提取。

磁流体陀螺;微弱信号;小波去噪;自相关;自适应阈值

随着高分辨率对地观测、高精度指向等卫星平台与应用技术发展,卫星平台及其有效载荷对于微角颤振的高精度测量和控制需求迫切。然而,当前卫星姿态控制系统中所采用的机电式陀螺仪、光学陀螺仪等均不能满足对测量精度和带宽的要求,上述陀螺仪低噪声和宽带宽的性能是相矛盾的,即在带宽较大时,精度会降低,在其综合性能的提升方面存在极大困难;磁流体陀螺作为一种新型角速度传感器,可以同时满足卫星微角颤振在轨测量的亚微弧度测量精度及千赫兹带宽的技术要求[1]。磁流体陀螺特别适用于空间工程应用,已应用于美国中继卫星反射镜试验RME[2]、日本先进陆地观测卫星ALOS[3]、美国静止轨道环境卫星GOES-N[4]等高精度航天器,是目前卫星微角颤振测量仪器的主要技术发展方向[5]。

与基于其他原理的陀螺仪相似,作为一种高精度的惯性传感器件,磁流体陀螺同样面临着微弱信号提取与检测的问题,其所探测的微弱宽频信号往往湮没在大量噪声中。目前,国内针对磁流体陀螺的研究较为落后,国外关于磁流体陀螺微弱信号提取与检测方法的研究也鲜有报道。美国休斯飞机公司(Hughes Aircraft Company)的Charles Pinney和Mark A Hawes介绍了磁流体角速度传感器本底噪声的测量方法,以及利用本底噪声预测传感器漂移误差的方法[6]。河北工业大学的孙景峰等人设计了一种磁流体加速度传感器,并设计了一套包括放大、滤波的预处理电路和数据显示电路[7]。天津大学于翔等人进行了单流体环磁流体陀螺仪的角振动跟踪实验。其所研究的磁流体陀螺输出经过前置放大和带通滤波后在单一频率下显示了良好的角振动信号跟踪性能[8]。

磁流体陀螺所检测的航天器微角振动幅值一般在sub-μrad至几百μrad之间,振动频率在1 kHz以内,且其工作于环境恶劣的宇宙环境中,前级传感器输出信号达到nV级,极其微弱,因此研究其微弱信号的检测方法是研发磁流体陀螺的关键技术之一。微弱信号检测最常见的方法主要包括相关检测、取样积分、锁相放大和双路消噪法等。但是这些方法或限制输入信号为单频信号或精度低、噪声大等原因并不适合所设计的磁流体陀螺的信号检测[9-11]。近年来兴起的小波变换具有多分辨率特性[12],能更有效地处理信噪比极低的信号,并且很好地保存有用信号中的尖峰部分和突变部分[13]。然而传统的小波阈值去噪算法基本是基于大量实验确定固定的分解层数及阈值,计算量大且针对不同信号的适应性差,特别是当陀螺输入信号并不确定时,会使去噪效果不明显或过度去噪而使有用信号失真。

针对这些问题,本文提出了一种基于自相关的小波去噪算法,通过计算小波分解各层细节分量的自相关系数,确定最佳分解层数,并通过该自相关系数确定自适应的收缩阈值,该方法极大地提高了磁流体陀螺输出信号的信噪比。文章第1部分陈述了磁流体陀螺的工作原理及机械结构,第2部分对经过预处理的输出信号进行了分析,第3部分提出基于自相关的小波去噪算法,第4部分进行实验验证并给出实验结果。

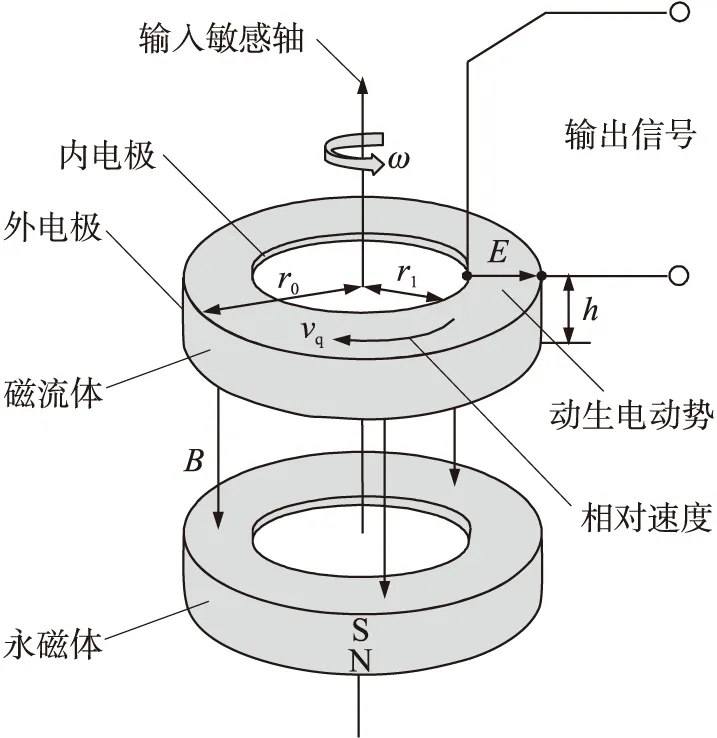
图1 磁流体陀螺工作原理示意图

1 磁流体陀螺工作原理及机械结构

磁流体陀螺工作原理基于磁流体动力学效应(MHD),即导电流体速度场与磁场的耦合效应。如图1所示,下层环为永磁体,提供强外磁场。上层环为流体通道,内部装满磁流体。当外界在磁流体陀螺的敏感轴方向有角速度ω输入时,永磁体及流体通道相对惯性空间产生角位移,而磁流体惯性较大,相对于惯性空间几乎静止,因此在磁流体和磁场间产生一个相对速度νq。磁流体切割磁感线,从而在金属外壳和芯柱之间产生与ω成线性关系的动生电动势E[14]:

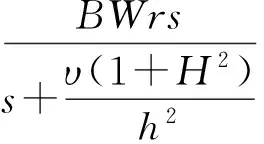
(1)

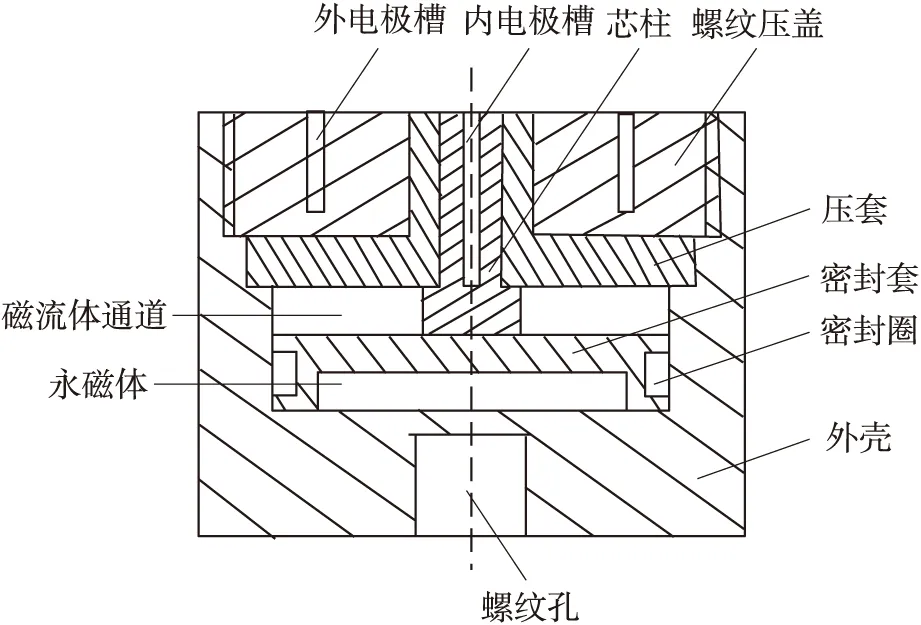
图2 磁流体陀螺机械装配图

基于上述原理,设计的磁流体陀螺结构如图2所示,圆柱体外壳选用高磁导率的软磁材料,为永磁体形成闭合磁回路,同时构成流体通道的外壁。外壳内底部放置圆片状永磁体,上面用绝缘的密封套卡住,密封套构成流体通道下表面。密封套侧面用密封圈密封,防止磁流体流入缝隙与永磁体接触;芯柱采用导电材料并构成流体通道内壁;压套压在芯柱的轴肩与外壳下孔肩上,作为流体通道的上壁;螺纹压盖紧压在压套上,与外壳螺纹配合,压套与外壳接触面涂抹环氧树脂胶,以防止磁流体溢出流体通道。螺纹压盖与芯柱分别钻有电极槽,安装电极,方便信号处理电路采集流体通道内、外壁电位信号。

2 输出信号分析

当外界输入角振动幅值达到μrad级别时,磁流体陀螺前级传感器的输出只有几十nV,对于磁流体陀螺微弱信号的提取,应首先将电压信号经过预处理电路进行放大并初步去噪。放大电路至少要提供1 000倍放大,并且要保证1 kHz的带宽,因此放大电路采用两级级联电路放大的形式,根据实验中传感器输出信号大小,将电路放大倍数设置为2000。对于级联电路而言,要降低预处理电路系统的噪声系数,可以通过提高第1级的增益和减小第1级的噪声来实现[15]。信号经过放大后,大量噪声也相应被放大,因此预处理电路中在每级放大器后进行了二阶低通滤波滤除高频噪声,截止频率为1kHz。

当输入角速度信号为频率1 Hz、幅值1 V的正弦波时,实验测得的电路输出信号及其频谱如图3所示。

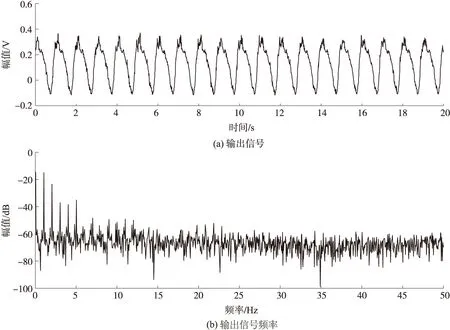
图3 磁流体陀螺输出信号及频谱

预处理电路中的滤波电路是基于频域的处理方法,这种方法要在信号频谱和噪声频谱没有重叠的前提下,才能把信号和噪声完全分开。实际中有用信号的频谱和噪声频谱往往是重叠的,信号经过低通滤波滤除了高频噪声,但是通带内的机械本体噪声,转台机械噪声,普通放大器1/f噪声、外界干扰噪声与白噪声等大量噪声经过预处理电路后相应地被放大,造成部分有用信号被噪声所湮没。由图3可以看出,电路输出信号仍然含有许多倍频信号及白噪声,导致有用信号部分湮没在噪声中,难以较好地检测角速度信息。

在实际中,陀螺要检测的信号可能包含许多尖峰或突变部分,并且噪声也不是平稳的白噪声。对这种信号的降噪处理,用传统的傅立叶变换分析,显得无能为力。而小波分析能将信号中各种不同的频率成分分解到互不重叠的频带上,并且可以根据信号特点,灵活的选择分解尺度、阈值及阈值函数,因此根据输出信号的特点,本文提出了一种基于自相关的小波改进去噪算法,旨在有效分离磁流体陀螺的有用信号和噪声,提高信噪比。

3 基于自相关的小波阈值去噪

相对来说,小波变换后,信号的小波系数值必然大于那些能量分散且幅值较小的噪声的小波系数值[16]。因此,小波阈值去噪的基本思路是将含噪信号在各尺度上进行小波分解,对细节分量设定一个阈值,幅值低于该阈值时,将其置零,高于该阈值时对其做相应的收缩处理,最后重构出有效信号。本文针对所设计的磁流体陀螺输出信号的特点,提出了基于自相关的小波阈值去噪算法,其基本流程如图4所示。首先将含噪信号进行一层小波分解,计算该层细节分量的自相关系数,判断其大小,若未显著增大,说明细节分量中包含的主要是噪声,则有必要再进行一层分解,然后重复上述过程,否则将该层设置为最优分解层数停止分解,然后根据各层细节分量的自相关系数确定各层自适应的去噪阈值,根据该阈值对各层细节分量作收缩处理,最后根据处理后的细节分量和近似分量重构出有效信号。

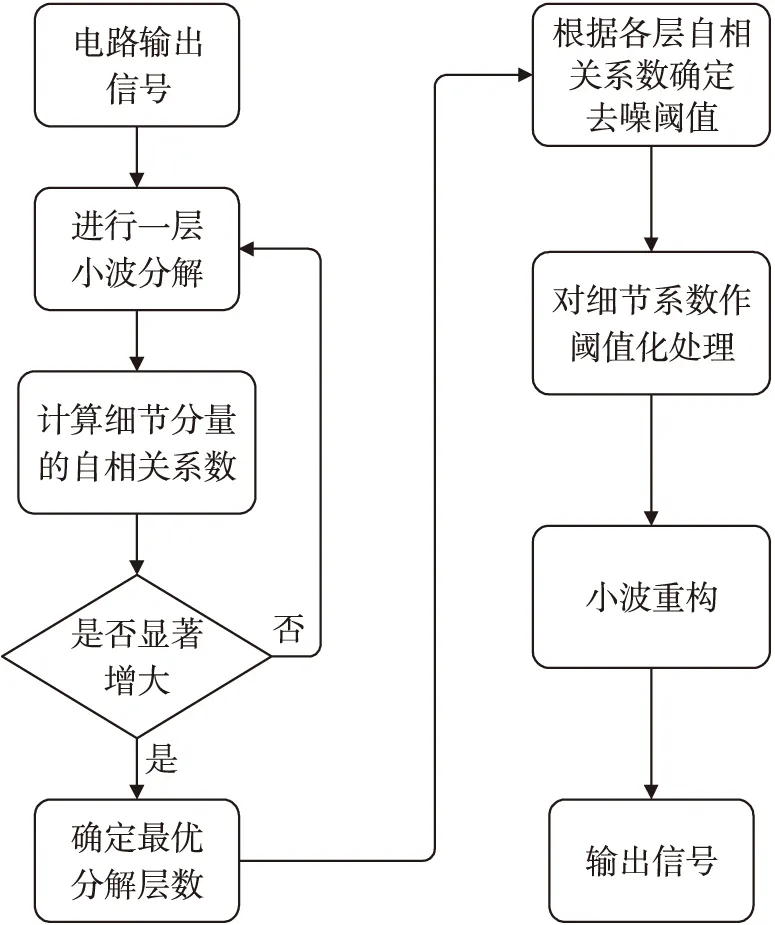
图4 改进小波去噪算法流程图

3.1 最优分解层数的改进选取方法

在实际应用中,根据不同研究对象,最优分解层数也不尽相同。若分解层数过多,可能会丢失信号的奇异性;而分解层数过少,则可能导致残留噪声较多[17]。在小波分解层数的问题上并没有严格的指标和依据法则,所以传统小波去噪方法只能通过大量的实验才能知道适合的分解层数,工作量大而效率低,实时性差。

根据小波去噪的原理可知,在信号分解的细节分量中,随着分解尺度的增大,有用信号幅度逐渐增加,而噪声不能在尺度间传递。由于信号只与信号本身相关,与噪声不相关,而噪声一般也是不相关的,那么可以通过计算细节分量的自相关系数αj来决定是否继续进行分解运算,如果自相关性系数αj非常小,则说明细节分量中包含的主要是噪声,则有必要再进行一层分解;如果自相关系数αj较大,则说明细节分量中包含了相当多的有用信号,那么便可以终止小波分解。从而确定最优小波分解层数k。

3.2 根据自相关系数求解各层阈值

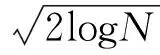
由于各层细节分量的自相关系数αj反映了其中所含信号及噪声比重的大小,因此可以将它作为区分信号和噪声的标准。实验发现,随着分解尺度的增加,细节分量的自相关系数αj迅速增大,之后趋于稳定,说明噪声分量开始较大,随着分解尺度的增加迅速减小,在较高分解尺度上,噪声引起的小波系数幅值很小,这就需要小波阈值在较小分解尺度上取较大值,从而尽可能多地去除噪声,随分解尺度增加阈值应该迅速减小并趋于稳定,从而保留更多的有用信号。指数函数符合这一变化趋势,因此利用指数函数对传统固定阈值进行改进,构造了符合上述变化趋势的函数,如式(2)所示,其中,a,b,c为调节因子。

(2)

试验发现,就本文所设计的磁流体陀螺的输出信号而言,当a=20,b=20,c=2时,去噪效果较好。

3.3 对小波分量进行阈值量化

传统阈值函数分为硬阈值和软阈值两种。硬阈值函数处理得到的估计小波系数连续性差,因此重构信号可能会产生振荡;而软阈值方法估计的小波系数虽然连续性好,但是当小波系数较大时,估计系数与真实系数间总存在恒定的偏差,这将直接影响重构信号与真实信号的逼近程度。本文采用了西北工业大学赵玉珍等人提出的改进阈值函数进行处理。阈值函数[20]为:

(3)

由该方法估计出来的数据ωj,k的大小是介于软、硬阈值方法之间的。当|ωj,k|≥λ时,ωj,k为非线性函数,且当|ωj,k|不断增大时,ωj,k越来越接近于ωj,k。

最后,根据小波分解的第k层的近似分量和经过阈值量化处理后的第l层到第k层的细节分量ωj,k进行一维信号的小波重构。

4 小波降噪实验

图5 磁流体陀螺测试平台示意图

实验平台如图5所示。将磁流体陀螺样机固定于速率转台上,用信号发生器向转台控制端输入单一频率正弦信号模拟待测角振动信号,角速度可以根据转台测速电机反馈电压信号计算得到。在示波器上观测磁流体陀螺预处理电路输出信号及转台测速电机反馈电压信号。利用Labview采集卡分别采集不同情况下系统输入信号及磁流体陀螺输出信号数据,传输到计算机后利用MATLAB进行小波处理。本实验分别采集了不同频率、不同输入幅值时的输出数据及相应的理想信号进行处理分析。

图6 输出信号6层小波分解系数

以1 Hz频率下,磁流体陀螺输出信号幅值为100 μV时的信号处理实验为例,由于实验所用输入信号为正弦信号,根据自相似原则及大量实验,选取了sym6作为小波基函数。利用sym6小波基对1 Hz电路输出信号进行6层小波分解,得到每一层的近似系数和细节系数如图6所示。

通过自相关式(4)可以计算出第j层细节系数cdj的自相关系数。

(4)

其中,k为延迟项,取k=9。计算可得|α1|=7.12×10-6,|α2|=2.03×10-5,|α3|=2.32×10-5,|α4|=3.3×10-3,|α5|=0.0288,|α6|=0.7305。一般认为:相关系数在0.00～±0.30之间,表示微相关;在±0.30～±0.50之间,表示实相关;在±0.50～±0.80之间,表示显著相关;在±0.80～±1.00之间,表示高度相关。由此可知,第1层到第5层的自相关系数值很小,说明其细节分量主要由噪声引起,需要对该层分量做较强的消噪处理,第6层的自相关系数值有了显著的增大,显示高度相关,说明该层细节分量已经出现了大量的有用信号,要尽可能地保留该层分量。因此噪声信号主要集中在前5层的细节分量中,则最优分解层数为5层。根据本文提出的改进阈值算法式(2),可以求得第1层到第5层的阈值分别为λ1=0.1520,λ2=0.1520,λ3=0.1520,λ4=0.1497,λ5=0.1306。

利用前述的阈值函数结合各层阈值对细节系数做阈值量化处理,然后对信号进行一维小波重构,可以得到小波去噪后的信号如图7所示。

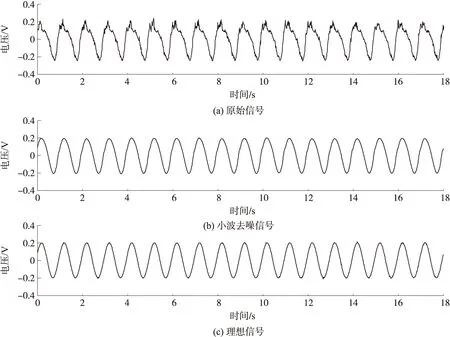
图7 原始信号、小波去噪信号和理想信号波形

图8 小波去噪结果与理想信号波形对比

分别利用传统小波去噪方法和本文提出的改进小波去噪方法对传感器输出信号进行对比处理,得到处理后的波形与理想波形如图8所示,图8(a)为应用传统小波去噪方法处理1 Hz信号后得到的对比波形,图8(b)为应用本文提出的改进小波去噪方法处理1 Hz信号后得到的对比波形。

利用式(5)分别计算不同频率下、不同幅值的信号经过处理后与理想信号之间的标准差,它可以衡量处理后的信号与理想信号的接近程度,计算结果如表1和表2所示,表1中数据为不同频率下幅值为100 μV的陀螺输出信号经过小波处理后与理想信号的标准差,表2为1 Hz频率下不同幅值的陀螺输出信号经过小波处理后与理想信号的标准差。

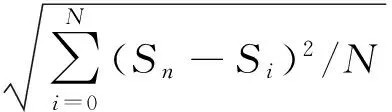
(5)

其中,Si为理想信号,本实验中将传感器输入信号作为理想信号,Sn为预处理电路输出信号。

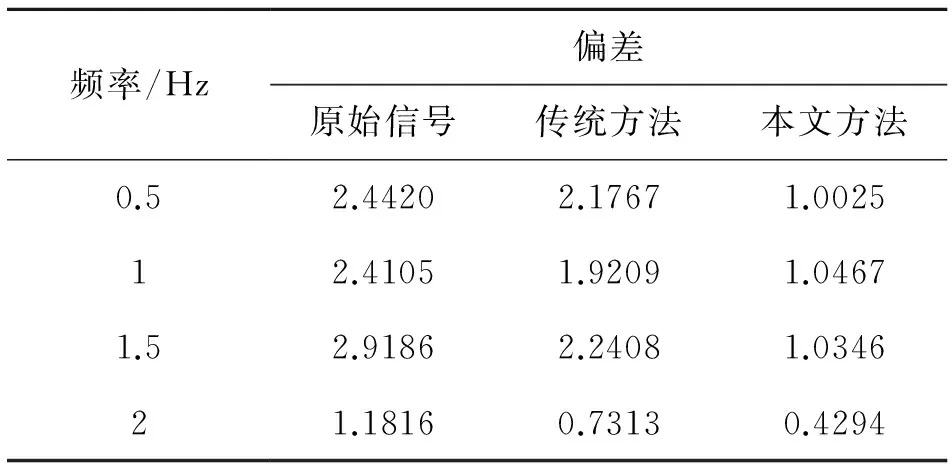
表1 不同频率下100 μV信号小波处理的标准差

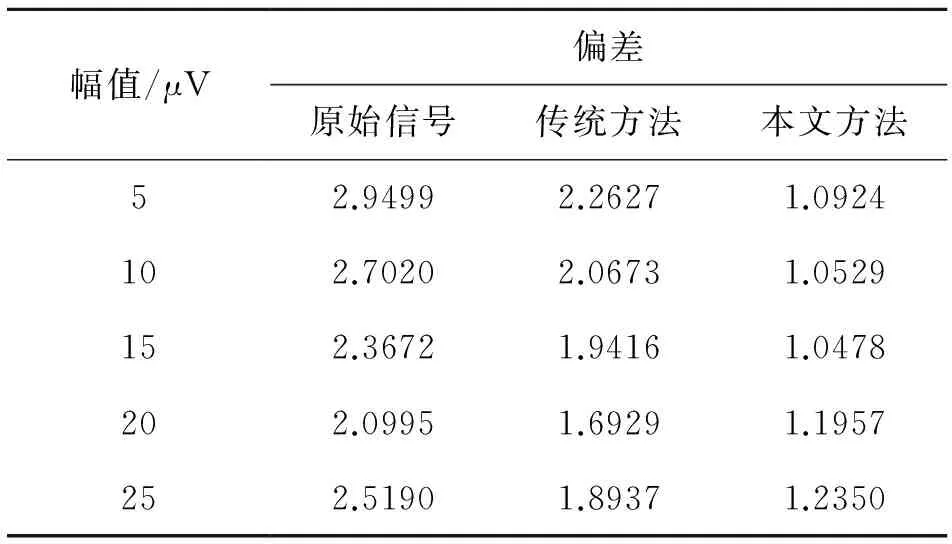
表2 1 Hz频率下不同幅值信号小波处理的标准差

由图8、表1和表2中数据可知,本文提出的小波改进去噪算法可以显著的改善输出信号的波形,降低输出信号与理想信号间的标准差,信号去噪效果良好。

信噪比可以衡量一个信号受噪声干扰的水平,信噪比计算公式[21]如下:

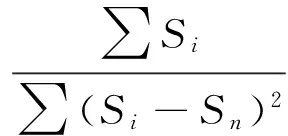
(6)

利用传统方法和改进方法对采集数据进行处理,利用式(6)对两种方法处理后得到的信号进行信噪比计算,结果如表3和表4所示,表3为不同频率下幅值为100 μV的陀螺输出信号经过小波处理后的信噪比,表4为1 Hz频率下不同幅值的陀螺输出信号经过小波处理后的信噪比,其中,信噪比提升为小波处理后的信号的信噪比减去原始信号的信噪比得到的差值。

表3 不同频率下100 μV信号处理的信噪比

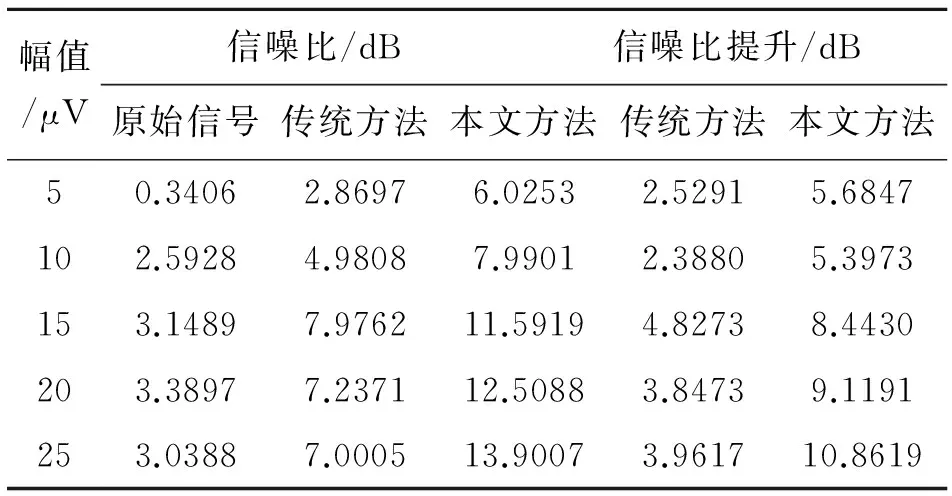
表4 1 Hz频率下不同幅值信号处理的信噪比

由表3和表4中的数据可以看出,将本文提出的小波改进去噪算法应用于所设计的磁流体陀螺微弱信号的提取与处理中,可以显著地提高信噪比。其中表4中信号的信噪比明显低于表3中信号的信噪比,这是因为信噪比计算公式中用到的理想信号为输入传感器的正弦信号,而实验所用转台在输入幅值较小时响应较差,其运动与输入正弦信号存在一定偏差,且幅值越小偏差越大,该偏差被磁流体陀螺感应输出后造成信号信噪比降低。同时有用信号幅值减小也会造成信号信噪比降低,但是从表中数据仍然可以看出,相对于传统小波去噪方法而言,本文提出的小波改进去噪算法去噪效果较为显著,适合于所设计的磁流体陀螺微弱信号的提取。

5 结论

本文针对所设计的磁流体陀螺传感器,设计了其信号预处理电路,并对电路输出信号的特点进行了分析,提出了一种改进的小波阈值去噪方法。本方法主要基于小波去噪理论以及信号相关性算法。首先,对磁流体陀螺输出信号进行小波分解,其最优分解层数可通过各层细节分量的自相关系数确定,然后对各层细节分量作阈值处理,所选阈值可由上述自相关系数来估计,最后根据处理后的细节分量重构回原信号。通过实验研究与计算分析,结果说明将改进的小波去噪方法应用于所设计的磁流体陀螺微弱信号的提取与处理中,可以极大地提高传感器输出信号的信噪比,降低输出信号与理想信号之间的标准差,从而有效地实现磁流体陀螺检测角速度的功能,进一步提高磁流体陀螺的分辨率及测量精度。

[1] 霍红庆,马勉军,李云鹏,等. 卫星微角颤振高精度测量技术[J]. 传感器与微系统,2011,30(3):4-6.

[2]Anspach J E,Sydney P F,Hendry G. Effects of Base Motion on Space-Based Precision Laser Tracking in the Relay Mirror Experiment[C]//International Society for Optics and Photonics,1991:170-181.

[3]Iwata T,Kawahara T,Muranaka N,et al. High-Bandwidth Attitude Determination Using Jitter Measurements and Optimal Filtering[C]//AIAA Guidance,Navigation,and Control Conference. 2009:7349-7369.

[4]GOES-N. Data Book[M]. Boeing Satellite Development Center,2006. 78-87.

[5]Laughlin D R,Hawes M A,Blackburn J P,et al. A Low-Cost Alternative to Gyroscopes for Tracking System Stabilization[C]//International Society for Optics and Photonics,1990:2-13.

[6]Pinney C,Hawes M A,Blackburn J. A Cost-Effective Inertial Motion Sensor for Short-Duration Autonomous Navigation[C]//Position Location and Navigation Symposium,1994,IEEE. IEEE,1994:591-597.

[7]孙景峰,杨庆新,张闯,等. 磁流体加速度传感器外围电路的研究与设计[C]//电工理论与新技术学术年会论文集,2005. 50-53.

[8]于翔,李醒飞,徐梦洁,等. 一种磁流体陀螺的设计研究[J]. 传感技术学报,2013,(11):1483-1487.

[9]Wang J,Yang L,Gao L,et al. Current Progress on Weak Signal Detection[C]//Quality,Reliability,Risk,Maintenance,and Safety Engineering(QR2MSE),2013 International Conference on. IEEE,2013:1812-1818.

[10]曹文晖. 基于Duffing振子和小波变换的微弱信号检测方法[D]. 中南大学,2011:2-4.

[11]Chunyan N,Zhuwen W. Application of Chaos in Weak Signal Detection[C]//Measuring Technology and Mechatronics Automation(ICMTMA),2011 Third International Conference on. IEEE,2011,1:528-531.

[12]Fan Z,Cai M,Wang H. An Improved Denoising Algorithm Based on Wavelet Transform Modulus Maxima for Non-Intrusive Measurement Signals[J]. Measurement Science and Technology,2012,23(4):045007.

[13]Mallat S,Hwang W L. Singularity Detection and Processing with Wavelets[J]. Information Theory,IEEE Transactions on,1992,38(2):617-643.

[14]Laughlin D R,Sebesta H R,Eckelkamp-Baker D. A Dual Function Magnetohydrodynamic(MHD)Device for Angular Motion Measurement and Control[J]. Advances in the Astronautical Sciences,2002,111:335-347.

[15]史文俊. L波段低噪声放大器的设计与实现[D]. 天津:南开大学,2009.

[16]Mallat S,Hwang W L. Singularity Detection and Processing with Wavelets[J]. Information Theory,IEEE Transactions on,1992,38(2):617-643.

[17]方琳,申冲,陈熙源. 基于小波多尺度变换的光纤陀螺振动误差分析与补偿[J]. 传感技术学报,2012,25(7):902-906.

[18]Donoho D L,Johnstone I M. Ideal Spatial Adaption Via Wavelet Shrinkage[J]. Biometrika,1994,81:425-455.

[19]Jiang J,Guo J,Fan W,et al. An Improved Adaptive Wavelet Denoising Method Based on Neighboring Coefficients[C]//Intelligent Control and Automation(WCICA),2010 8th World Congress on. IEEE,2010:2894-2898.

[20]赵瑞珍,王红. 小波系数阈值估计的改进模型[J]. 西北工业大学学报,2001,19(4):625-628.

[21]Baili J,Lahouar S,Hergli M,et al. GPR Signal Denoising by Discrete Wavelet Transform[J]. NDT and E International,2009,42(8):696-703.

王丽萍(1990-),女,天津大学硕士研究生,主要研究方向为惯性器件制造与测试系统,wliping@tju.edu.cn;

李醒飞(1966-),男,天津大学精密仪器与光电子工程学院副院长,天津大学空间仪器与技术研究所所长,教授,博士生导师,主要研究方向为多传感器融合技术、机电惯性器件与系统以及海洋环境监测技术。现兼任中国机械工程学会高级会员,中国仪器仪表学会精密机械分会常务理事,lixf@tju.edu.cn。

ResearchoftheWaveletDenoisingAppliedtotheWeakSignalDetectionoftheMagnetofluidGyroscope*

WANGLiping1,LIXingfei1*,WUTengfei1,JIYue1,XUMengjie1,CHENCheng2

(1.State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China;2.College of Mechanical Engineering,Tianjin University of Commerce,Tianjin 300134,China)

New magnetofluid gyroscope which is superior to the gyroscope used in the current satellite system can meet the technical requirements of the submicron measurement accuracy and the kHz bandwidth in the In-orbit measurement of the satellite micro angle vibration,It’s an ideal sensor widely used in measurement of satellite micro angle vibration. But its output signal which is drowned into a lot of noise is so weak that the angular velocity can’t be detected effectively.A wavelet denoising method is proposed using self-correlation to extract the weak signal. This method can choose the optimal wavelet decomposition level and denoising threshold based on the self-correlation coefficient of the detail components. A comparative experiment was made between the traditional wavelet denoising method and the method proposed in this paper. The results show that the SNR of the output signal could be improved by 7 dB～10 dB and it is suitable for the weak signal detection of the magnetofluid gyroscope.

magnetofluid gyroscope;weak signal;wavelet denoising;self-correlation;Adaptive Threshold

项目来源:国家自然科学基金项目(61304243)

2014-05-29修改日期:2014-09-01

10.3969/j.issn.1004-1699.2014.10.010

TH73;TN911.23

:A

:1004-1699(2014)10-1355-08