线性最小二乘法的RSSI定位精确计算方法*

袁 鑫,吴晓平,2*,王国英,2

(1.浙江农林大学信息工程学院,浙江 临安 311300;2.浙江省林业智能监测与信息技术研究重点实验室,浙江 临安 311300)



线性最小二乘法的RSSI定位精确计算方法*

袁 鑫1,吴晓平1,2*,王国英1,2

(1.浙江农林大学信息工程学院,浙江 临安 311300;2.浙江省林业智能监测与信息技术研究重点实验室,浙江 临安 311300)

基于接收信号强度指示(RSSI)定位模型,提出了一种目标节点位置的精确计算方法。将RSSI定位问题所描述的非线性优化函数转化为线性最小二乘法估计问题,将定位结果直接用代数解表示。分别提出了目标节点信号发射强度已知和未知下的非约束线性最小二乘(ULLS)定位方法。同时对非约束线性最小二乘法下的参数进一步优化,提出了约束线性最小二乘法以提高定位精度。仿真验证了该定位计算方法的有效性,测试了不同信号强度噪声对定位误差的影响。结果同时表明,约束线性最小二乘法比非约束线性最小二乘法的定位误差更小,非常接近于定位结果的克拉美罗下界值(CRLB)。

无线传感器网络;定位;无线信号强度;线性最小二乘法

无线传感器网络(WSNs)是通过将大量具有传感器单元、数据处理单元及通信模块的微小智能节点密集地散布在感知区域,节点间以自组织方式构成的无线通信网络。无线传感器网络能够实时监测、感知和采集网络分布区域内的各种环境或监测对象的信息,并对这些信息进行处理,从而为远程用户提供详尽而准确的信息[1]。采用无线传感器网络进行信息收集和处理,这些数据必须和位置信息相结合才有意义,甚至有时需要传感器节点发回单纯的位置信息[2-4]。无线传感器网络以其廉价的无线通信组网而区别于其他无线通讯技术。从应用角度来讲,节点定位是无线传感器网络中最为重要和传统的问题,研究具有低成本、高精度的无线传感器网络定位系统是该领域的主要问题之一。传统的测距定位方法,如到达时间(TOA)[5-6]、到达时间差(TDOA)[7]、到达角度(AOA)[8]等能获取较高的定位精度,但需要额外的测距硬件设施,增加了定位成本,且节点间的测距易受环境、节点硬件、网络攻击等各种因素的干扰。以节点的连通性、网络拓扑为基础的非测距定位方法[9]亦能定位节点坐标,但定位精度不高,限制了其使用范围。

数据感知与信号传输是无线传感器网络节点的基本内容,节点间以电磁波的形式进行相互通信,无线信号强度随传输路径的延长而衰减。在无线传感器网络领域,接受信号强度指示(RSSI)距离测量被认为是一种具有较高性价比的方法。RSSI定位方法无需额外硬件,实现简单,具备低功耗、低成本等特点,应用十分广泛[10-11]。最大可能(ML)估计方法能达到定位结果的克拉美罗下界(CRLB),文献[12]将ML估计方法应用于能量定位模型,并提出了相应的多目标定位实现方法。为改进强噪声对定位结果的严重干扰,根据RSSI定位模型Wang等[13]提出了半正定(SDP)放松的方法以精确定位目标位置,但由于SDP方法进行了约束放松,定位精度没能达到CRLB,且SDP定位方法的计算复杂度较高。亦有文献将定位模型所描述的非线性优化函数转化为其他数学模型问题,如Ho等[14]将非线性过程转化为线性方程,提出了一种线性代数解法亦能精确目标节点位置,但该计算方法未考虑目标节点发射强度未知下的最优估计结果。虽然ML方法的定位精度较高,但计算复杂度较大,基于自校正RSSI测距模型Coluccia[15]提出了一种低复杂度的ML定位方法。

ML估计方法的数值解法有可能产生局部最优解,导致定位结果不稳定。本文针对无线信号强度RSSI的定位模型,提出了目标节点信号发射强度已知和未知两种情况下的目标节点位置的精确代数计算方法。该定位计算方法以ML估计方法所描述的非线性优化函数为出发点,将非线性优化函数转化为线性最小二乘估计问题,并将定位结果直接用代数解表示,以提高定位结果的稳定性。在建立的非约束线性最小二乘(ULLS)法的求解基础上,利用向量元素间的相互约束关系,推导了约束线性最小二乘(CLLS)的计算方法,提高了定位精度。

本文第1部分首先介绍了RSSI定位模型;第2部分推导了RSSI模型定位结果CRLB下界值;第3部分推导了目标节点信号发射强度已知和未知两种情况下的ULLS和CLLS定位计算方法;第4部分为仿真与分析;最后部分为结论。

1 RSSI定位模型

假设在二维坐标平面上分布着N个信标节点,信标节点i位置坐标为xi=[xiyi]T(i=1,2,…,N)。设x=[xy]T表示被定位目标节点坐标,目标节点与信标节点i间的无线接收信号强度为pi。假设节点间的RSSI测距服从对数衰减模型,则节点间RSSI信号强度pi与相对距离的有关系式

pi=p0-10βlgdi+εi

(1)

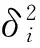
(2)

式(2)所描述的非线性最小平方问题可以采用数值计算方法求解,如高斯牛顿迭代法或Levenberg-Marquardt(LM)算法迭代求解。采用数值计算方法时,可能会陷入局部最优,使定位结果发散。为此将式(2)描述的非线性优化函数转化为线性最小二乘估计问题,其定位结果采用代数解表示,提高定位结果的可靠性。

2 定位结果CRLB

CRLB为模型待估目标位置x的无偏估计提供了误差方差的下界,x满足cov(x)≥F-1,这里F为待估参数x的FIM(Fisher Information Matrix)的表示。以对数衰减模型描述的信号强度与节点间距离关系,与待定位节点的发射信号强度p0有关。下面分别根据发射信号强度p0已知和未知两种不同情况下的定位结果CRLB进行分析。

2.1 已知发射信号强度p0

当p0已知时,则矩阵F可以表示为

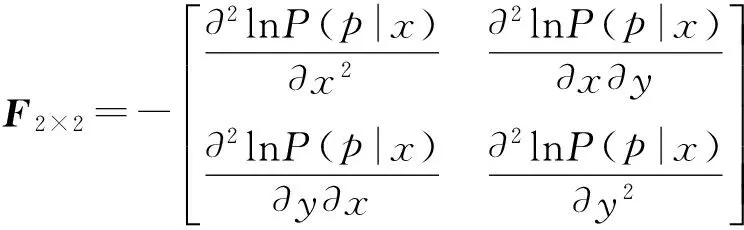
(3)

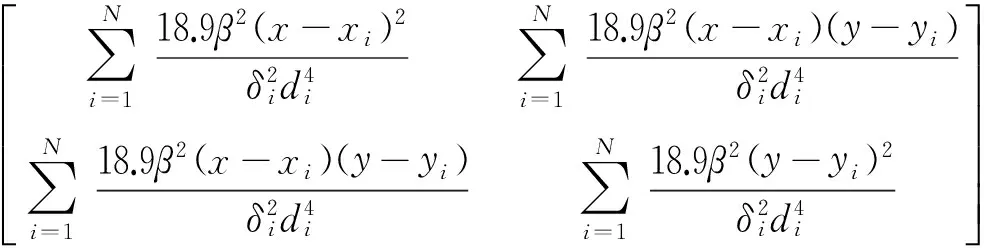
(4)

则根据CRLB无偏估计下界理论有

(5)

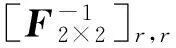
2.2 未知发射信号强度p0

由于发射信号强度p0未知,矩阵F可以表示为

(6)

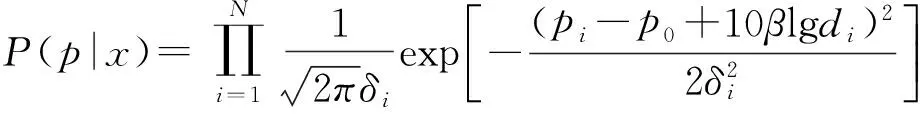
(7)

3 线性最小二乘法定位

下面分别根据发射信号强度p0已知和未知两种不同情况下采用线性最小二乘法计算目标节点坐标x。

3.1 已知发射信号强度p0

对式(1)进行变换,改写为

(8)

式(8)中,i=1,2,…,N。对式(8)右边采用泰勒级数展开,忽略高阶项,将式(8)再变换为

(9)

(10)

式(10)中,i=1,2,…,N。令z=[xyx2+y2]T,可将式(10)写成线性矩阵形式

Az=b+α

(11)

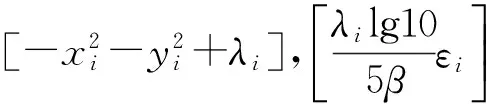
根据线性最小二乘平方原理,参数z的无偏估计值为

z=(ATWαA)-1ATWαb

(12)

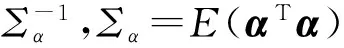
(13)

式(13)中,i,j=1,2,…N。

假设参数z的估计误差为Δz,其值为

Δz=(ATWαA)-1ATWαα

(14)

估计误差Δz的方差为

cov(Δz)=(ATWαA)-1

(15)

从参数z提取出z(1:2)即为被定位目标节点坐标。上述求解过程并未考虑向量z=[xyx2+y2]T中各元素的相互约束关系,把该计算方法称为已知发射信号强度p0下RSSI定位问题的非约束线性最小二乘(ULLS)方法。式(7)得到了被定位目标节点坐标的近似估计值,可利用向量z=[xyx2+y2]T元素间的相互约束关系计算其目标节点位置坐标精确值。被定位目标节点坐标的真实值假设为xo=[xoyo]T,则有以下关系式

(16)

式(16)中z(k)、Δz(k)表示了向量z、Δz的第k个元素,k=1,2,3。将式(16)表示为线性矩阵形式

Guo=h+β

(17)

根据线性最小二乘平方原理,向量uo的无偏估计为
u=(GTWβG)-1GTWβh

(18)

式(18)中维度为3×3的矩阵Wβ值为Wβ=E(βTβ)-1=[LTcov(Δz)L]-1=L-1ATWαAL-1

(19)

由于uo=[xo2yo2]T,则被定位目标节点坐标的精确估计值x为

(20)

将以式(20)表示的计算过程考虑了参数z中元素间的相互约束关系,进一步优化了定位结果,将此过程称为已知发射信号强度p0下RSSI定位问题的约束线性最小二乘(CLLS)方法。

3.2 未知发射信号强度p0

发射信号强度p0因节点的电池和天线增益不同而有所区别。下面就发射信号强度p0未知情况下的线性计算问题进行改进。

将式(9)变换为

(21)

Czρ=d+α

(22)

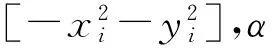
同样根据线性最小二乘平方原理,参数zρ的无偏估计值为

zρ=(CTWαC)-1CTWαd

(23)

式(23)中维度为N×N的矩阵Wα为最小平方权重系数,其值计算同式(13)。由于在计算权重系数Wα时,需要发射信号强度p0。可预先设置Wα为单位矩阵,近似地求解发射信号强度p0,然后以p0近似值计算Wα,再以式(23)精确计算参数zρ。同样从参数zρ提取出zρ(1:2)即为被定位目标节点坐标。此计算过程为未知发射信号强度p0下RSSI定位问题的非约束线性最小二乘(ULLS)方法。

同样地可利用向量z=[xyx2+y2]T元素间的相互约束关系计算目标节点坐标的精确值,具体计算过程可参考式(14)～式(20),此计算过程称为未知发射信号强度p0下RSSI定位问题的约束线性最小二乘(CLLS)方法。

4 仿真分析

根据发射信号强度p0已知和未知两种不同情况下的线性最小二乘ULLS和CLLS定位计算方法,采用MATLAB软件进行了算法仿真实现。假设被定位目标节点与每个信标节点间的信号强度噪声都服从均值为0,方差为δ2的高斯分布,仿真测试了不同计算方法下的定位结果。为评价文中不同算法下的定位效果,目标节点的定位精度采用均方误差(MSE)定位误差判断。

4.1 已知发射信号强度p0下的定位结果

无线传感器网络节点部署在100 m×100 m区域内,在该区域内将5个信标节点位置坐标预先设置在(20,30),(15,80),(40,15),(70,10),(15,90),将被定位目标节点坐标预先设置在(50,50)点。同时预先设置p0=-45 dB,路径衰减指数β=2。调整信号强度噪声,即调整参数δ2从0.12到12之间变化,即调整10lg(δ2)从-20 dB到0 dB之间变化,仿真测试了不同计算方法下的MSE定位误差。对每种定位算法下的MSE定位误差仿真运行1 000次,采用1 000次运行结果的平均MSE定位误差评价定位算法的定位精度,图1(a)绘出了ULLS和CLLS两种不同算法下的定位误差随噪声变化关系。从图1(a)可见,随着20lg(δ2)的增加,即信号强度噪声的增大,平均MSE定位误差也随之增大,20lg(MSE)定位误差与信号强度噪声20lg(δ2)之间有近似线性关系。当信号强度噪声等于-20 dB时,ULLS方法的定位误差20lg(MSE)为-3.9 dB,而CLLS方法的定位误差10lg(MSE)为-14.1 dB。相比于ULLS方法,CLLS方法的定位误差有较大减少,非常接近于定位结果的CRLB下界值。

图1 已知发射信号强度p0下的定位结果

设定信号强度噪声δ2为0.12,图1(b)绘出了1 000次随机测试下两种不同计算方法下定位结果的累积分布函数曲线(CDF)。显然ULLS方法的定位误差较大,而CLLS方法能有效改进定位误差。ULLS方法下90%定位结果MSE小于1.6 m2,而对于CLLS方法下90%的定位结果平方误差小于0.5 m2。

4.2 未知发射信号强度p0下的定位结果

无线传感器网络节点部署在100 m×100 m区域内,在该区域内将6个信标节点位置坐标预先设置在(20,30),(15,80),(40,15),(70,10),(15,90),(80,20),将被定位目标节点坐标预先设置在(50,50)点。同样地预先设置p0=-45 dB(计算过程中假设p0为未知数),路径衰减指数β=2。调整信号强度噪声,即调整参数δ2从0.12到12之间变化,即调整10lg(δ2)从-20 dB到 0dB之间变化,仿真测试了两种不同计算方法下的MSE定位误差。对每种定位算法下的MSE定位误差仿真运行1 000次,采用1 000次运行结果的平均MSE定位误差评价定位算法的定位精度,图2(a)绘出了ULLS和CLLS两种不同算法下的定位误差随噪声变化关系。从图2(a)可见,随着20lg(δ2)的增加,即信号强度噪声的增大,平均MSE定位误差也随之增大,20lg(MSE)定位误差与信号强度噪声20lg(δ2)之间有近似线性关系。当信号强度噪声等于-20 dB时,ULLS方法的定位误差20lg(MSE)为4.5 dB,而CLLS方法的定位误差10lg(MSE)为-12.4 dB。相比于ULLS方法,CLLS方法的定位误差有较大减少,非常接近于定位结果的CRLB下界值。

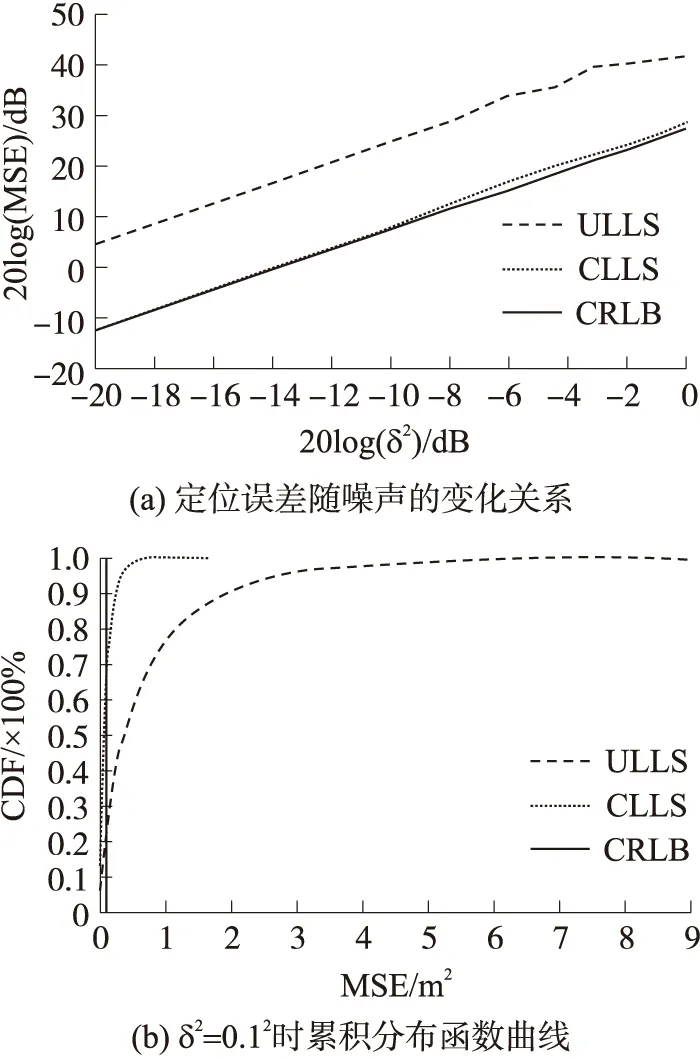
图2 未知发射信号强度p0下的定位结果

设定δ2为0.12,图2(b)绘出了1 000次随机测试下两种不同计算方法下定位结果的累积分布函数曲线(CDF)。显然ULLS方法的定位误差较大,而CLLS方法能有效改进定位误差。ULLS方法下90%定位结果MSE小于4.3 m2,而对于CLLS方法下90%的定位结果平方误差小于0.6 m2。

4.3 不同定位算法下的定位结果比较

以优化函数描述的最大可能性(ML)估计方法可以采用数值计算方法求解,但易于陷入局部最优,导致定位结果发生严重偏差。以LM数值算法计算式(2)所描述的优化函数,将此方法称为ML-LM定位方法。在100 m×100 m区域内随机生成将6个信标节点,将被定位目标节点坐标预先设置在(50,50)点。仿真运行1 000次,采用1 000次运行结果的平均MSE定位误差评价定位算法的定位精度。调整参数δ2从0.12到12之间变化,图3绘出了在3种不同计算方法下MSE的比较结果。由该图可见,ML-LM计算方法的平均MSE较大,而ULLS和CLLS方法的定位结果较稳定。通过观察ML-LM计算方法下的定位结果,发现有部分结果严重偏离(50,50)点,归结其原因是由于定位计算过程中陷入了局部最优。相比于ULLS方法,CLLS方法的定位误差都有所减少。

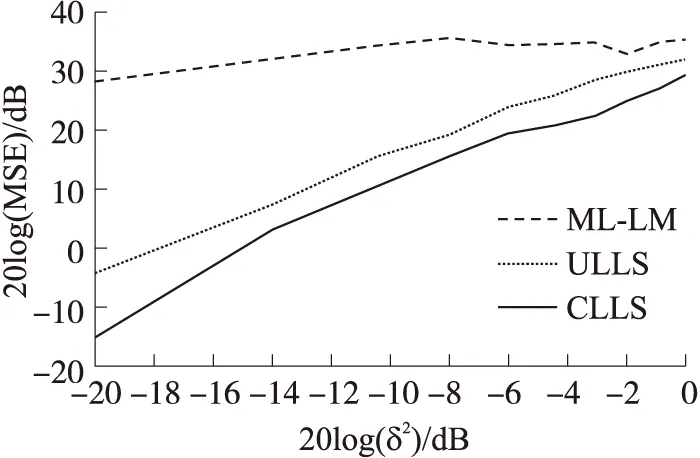
图3 不同定位算法下的定位结果比较

5 结论

本文介绍了RSSI定位模型下的目标节点位置精确定位方法,该方法以信号强度RSSI的对数衰减模型为基础。提出了发射信号强度p0已知和未知两种不同情况下的线性最小二乘ULLS和CLLS计算方法,以代数计算方法表示了目标节点的精确位置坐标。相比于ML-LM数值计算方法,ULLS和CLLS方法避免了数值解法中的局部最优问题,其代数计算方法的定位结果更加稳定,具有较好的定位精度。CLLS方法利用了向量间的相互约束关系,其定位结果非常接近于CRLB下界值。

[1] Mo Lufeng,He Yuan,Liu Yunhao,et al. Canopy Closure Estimates with GreenOrbs:Sustainable Sensing in the Forest[C]//Proceedings of the 7th International Conference on Embedded Networked Sensor Systems,SenSys 2009:99-112.

[2]Yang Zheng,Liu Yunhao. Understanding Node Localizability of Wireless Ad Hoc and Sensor Networks[J]. IEEE Transactions on Parallel and Distributed Systems,2012,11:1249-1260.

[3]蔡绍滨,高振国,潘海为,等. 带有罚函数的无线传感器网络粒子群定位算法[J]. 计算机研究与发展,2012,49(6):1228-1234.

[4]Zhao Jizhong,Xi Wei,He Yuan,et al. Localization of Wireless Sensor Networks in the Wild:Pursuit of Ranging Quality[J]. IEEE Transactions on Networking. 2013,12(1):311-323.

[5]Ismail Guvenc,Chia-Chin Chong. A Survey on TOA Based Wireless Localization and NLOS Mitigation Techniques[J]. IEEE Communications Surveys and Tutorials. 2009,11(3):107-124.

[6]Junyang Shen,Andreas F Molisch,Jussi Salmi. Accurate Passive Location Estimation Using TOA Measurements[J]. IEEE Transactions on Wireless Communications. 2012,11(6):2182-2192.

[7]Ho K C,Xu Wenwei. An Accurate Algebraic Solution for Moving SourceLocation Using TDOA and FDOA Measurements[J]. IEEE Transactions on Signal Processing. 2004,52(9):2453-2463.

[8]Dragos Niculescu,Badri Nath. Ad Hoc Positioning System(APS)Using AoA[C]//Proceeding of the IEEE Infocom. 2003,3:1734-1743.

[9]Zhang Shigeng,Cao Jiannong,Chen Lijun,etc. Accurate and Energy-Efficient Range-Free Localization for Mobile Sensor Networks[J]. IEEE Transactions on Mobile Computing. 2010,9(6):897-910.

[10]吴晓平,陆炳斌,沈浩. 基于RSSI定位模型的非视距关系识别方法[J]. 传感技术学报,2013,26(11):1584-1589.

[11]Robin Wentao Ouyang,Albert Kai-Sun Wong,Chin-Tau Lea. Received Signal Strength-Based Wireless Localization via Semidefinite Programming:Noncooperative and Cooperative Schemes[J]. IEEE Transactions on Vehicular Technology,2010,59(3):1307-1318.

[12]Sheng Xiaohong,Hu Yuhen. Maximum Likelihood Multiple-Source Localization Using Acoustic Energy Measurements with Wireless Sensor Networks[J]. IEEE Transactions on Signal Processing,2005:53(1):44-53.

[13]Wang Gang,Yang Kehu. A New Approach to Sensor Node Localization Using RSS Measurements in Wireless Sensor Networks[J]. IEEE Transactions on Wireless Communications,2011,10(5):1389-1395.

[14]So H C,Lin L. Linear Least Squares Approach for Accurate Received Signal Strength Based Source Localization[J]. IEEE Transactions on Signal Processing,2011,59(8):4035-4040.

[15]Angelo Coluccia. Reduced-Bias ML-Based Estimators with Low Complexity for Self-Calibrating RSS Ranging[J]. IEEE Transactions on Wireless Communications. 2013,12(3):1220-1230.

吴晓平(1977-),男,浙江金华人,博士,研究方向为无线传感器网络与分布式计算。作为主要技术骨干完成2项国家自然科学基金,1项国家973课题。在国内外重要会议及期刊上发表论文十多篇,其中SCI收录3篇,wuxipu@gmail.com。

AccurateComputationApproachofRSSI-BasedLocalizationwithLinearLeastSquareMethod*

YUANXin1,WUXiaoping1,2*,WANGGuoying1,2

(1.School of Information Engineering,Zhejiang A&F University,Lin’an Zhejiang 311300,China; 2.Zhejiang Provincial Key Laboratory of Forestry Intelligent Monitoring and Information Technology,Lin’an Zhejiang 311300,China)

Based on the localization model with received signal strength indication(RSSI),an accurate localization computation approach of target node position is proposed. Transforming the nonlinear optimization function depicted by RSSI localization model as the estimation problem of linear least square method,the localization results are directly represented as algebraic solutions. The localization approaches of unconstrained linear least square(ULLS)method are proposed with known and unknown transmission power of target node. The parameters of ULLS method are further optimized,then the constrained linear least square(CLLS)method is put forward to improve the localization accuracy. The simulations demonstrate the validity of the localization computation method and test the impacts of signal strength noises on localization error. The results also show that the localization error of CLLS method is less than that of ULLS method and very close to the Cramer-Rao low bound(CRLB)of localization error.

wireless sensor networks;localization;received signal strength indication;linear least square

项目来源:国家自然科学基金重大项目(61190114);国家自然科学青年基金项目(61303236);浙江省教育厅科研项目(Y201328700);浙江农林大学科研发展基金人才启动项目(2013FR086)

2014-05-23修改日期:2014-08-29

10.3969/j.issn.1004-1699.2014.10.020

TP393.0

:A

:1004-1699(2014)10-1412-06