移动锚节点凸规划定位算法研究及改进

任克强,庄放望

(江西理工大学信息工程学院,江西 赣州 341000)



移动锚节点凸规划定位算法研究及改进

任克强*,庄放望

(江西理工大学信息工程学院,江西 赣州 341000)

为了提高无线传感器网络的节点定位精度,对相关文献进行了研究,提出了一种改进的移动锚节点凸规划定位算法。该算法对原算法作了以下改进:利用正半定松弛方法扩大求解问题的可行域,以降低求解优化问题的计算复杂度;采用局部梯度下降法进行迭代优化来逼近最优估计,以提高优化问题的求解精度。实验结果表明,改进算法比原算法具有更高的定位精度,并可以更好地适应不同的网络规模。

无线传感器网络;定位算法;凸规划;梯度下降法;移动锚节点

在无线传感器网络WSN(Wireless Sensor Network)中,对于大部分的感知任务,例如路由协议效率、定位与跟踪、节点分簇等,获取传感器节点的位置信息极其重要[1]。节点定位是无线传感器网络的关键技术之一,根据定位过程中是否需要距离信息,可将定位算法分为测距相关与测距无关两大类[2]。典型的测距相关定位算法有基于到达时间TOA(Time of arrival)定位、基于到达时间差TDOA(Time Difference of Arrival)定位、基于到达角度AOA(Angle of Arrival)定位和基于接收信号强度指示RSSI(Received Signal Strength Indicator)定位等算法[3-4],典型的测距无关定位算法有质心定位,距离向量-跳段DV-hop(Distance Vector-hop)定位,凸规划定位、基于多维定标MDS(Multidimensional Scaling)定位等算法[5-6]。

近年来,通过优化方法来解决节点定位问题成为研究的热点之一,许多基于规划的定位方法逐渐被提出[7-8]。文献[9]提出Convex定位算法,该算法将传感器网络中的未知节点和锚节点能否进行通信作为约束条件,通过多个邻接锚节点的通信约束构造凸规划问题,但通过节点通信区域交集的外接矩形面积近似通信区域交集,降低了定位精确度。文献[10]提出了一种基于二阶锥规划松弛的分布式定位算法,尽管在凸包内的未知节点可获得较好的定位精度,但在凸包外的未知节点定位性能较差。文献[11]对二阶锥规划问题进行了改进,用半定松弛的方法把非凸规划问题转化为凸规划问题,从而根据距离约束采用极大似然准则计算节点的位置,但定位过程中需测量未知节点与锚节点的距离。文献[12]提出一种新的半定规划松弛方法将最大似然估计最小二乘问题转化为凸规划问题,但定位过程需使用RSS测距模型。文献[13]提出Co-SRL的凸规划节点定位算法,以多个移动锚节点进行协作定位,并采用凸规划方法计算节点的位置。文献[14]提出一种高斯噪声下基于最大分散度的半定规划定位算法,该算法利用半定规划,并用梯度下降法进行求精,取得了较好的定位精度。文献[15]利用移动锚节点以不同的功率发射信标信号,将未知节点接收到的信标信息转化为二次不等式约束组,再利用凸规划方法计算节点的位置,取得了较高的定位精度,但定位精度还可进一步提升。因此,本文对文献[15]的方法进行了改进,提出了一种改进的移动锚节点凸规划定位算法,以提高节点定位的精度。

1 凸规划定位算法

WSN中的锚节点与未知节点之间相互通信必须满足欧几里德距离的约束关系:

‖x-a‖≤R

(1)

其中,x为未知节点的位置,a为锚节点的位置,R为锚节点的最大传输半径。

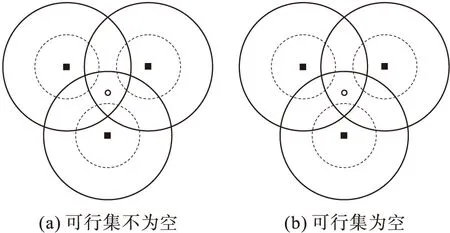
图1 两种定位情形

如果锚节点在不同位置以多种功率发射信标信号,则每个未知节点可获得与自身位置x有关的不等式约束组:

rk<‖x-ak‖≤Rkk=1,2,…,n

(2)

其中,ak为k时刻锚节点的位置,rk(可能为零)和Rk为k时刻的有效约束半径。

在多功率移动锚节点的WSN中,每个未知节点的定位问题可以转化为二次不等式组的求解问题。但网络环境因素的复杂性可能导致未知节点与锚节点之间不满足通信的条件,信号的干扰、衰减等因素也会对节点定位过程造成严重影响。因此,可能导致两种节点定位的情形,如图1所示。图1中的黑色方块表示锚节点位置,空心圆圈表示未知节点位置;图1(a)的可行集不为空,图1(b)的可行集为空。

文献[15]提出一种移动锚节点辅助的凸规划定位算法,该算法可适用于上述两种定位的情形,也可推广应用于测距相关的定位系统。

根据通信约束关系,每个未知节点可以得到一组关于自身位置的约束,并通过最小化得到最优位置的逼近。

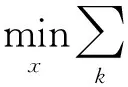
(3)

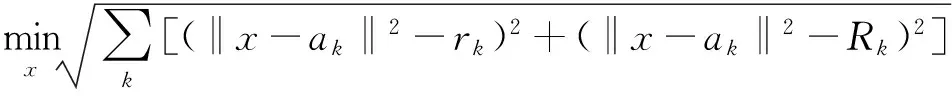
(4)

2 改进的凸规划定位算法

文献[15]利用凸松弛方法将式(4)的非凸规划问题转化为凸规划问题,但采用这种优化方法将会增加计算复杂度,并且导致求解结果出现非最优解或可行解,这无疑降低了规划问题求解的精度。本文对文献[15]的方法进行了改进,利用正半定松弛方法,扩大求解问题的可行域并降低求解优化问题的计算复杂度,采用局部梯度下降法提高优化问题的求解精度。

将式(3)展开得到:

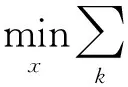
(5)

由于锚节点的有效半径可根据其发射功率计算得到,即rk和Rk已知,故:

(6)

由于式(6)为非凸规划问题,但可利用凸松弛方法将式(6)转化为凸规划问题。

令X=[x1,x2,…,xn]∈R2×n,Y=XTX,

μxa=‖x-ak‖2,vxa=‖x-ak‖

则式(6)中的范数部分为:

‖x-ak‖2=(ak;ei)T[I2;X]T[I2;X](ak;ei)

(7)

从而,式(6)可表示为:

(8)

其中,I2为2维单位矩阵,ei为第i个元素为1的n维单位向量,(ak;ei)为(2+n)维列向量。

根据非凸优化理论,可以通过半定松弛方法,将非凸规划问题转化为凸规划问题:

(9)

因此,可以得到式(9)凸规划问题的一般形式:

(10)

由于半定规划内点法产生的解具有高秩性,其松弛解可能不是最优解,甚至不是可行解。因此,通过局部梯度下降法来逼近最优解。

(11)

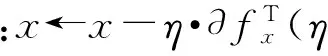
令精度为ε(ε>0),迭代次数为m(m的初值为1),则局部梯度下降法的步骤如下:

S1 以半定规划松弛解xi(i=1,2,…,n)为初始点开始迭代;

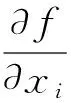
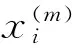
本文改进方法的计算复杂度和求解精度分析如下:

求解凸规划问题,一般情况下,采用内点法解决n个未知节点定位问题的计算复杂度与约束条件个数有关,如果约束条件的个数在O(n)范围内,其计算复杂度为O(n3)[16]。文献[15]模型引入松弛后,约束条件的个数在O(n2)范围内,故求解文献[15]规划问题的计算复杂度为O(n6)。而本文模型进一步松弛,式(10)中的(2+n)维矩阵锥Z可以被分解成小矩阵锥,分解后的约束条件个数在O(n)范围内,故求解本文凸规划问题的计算复杂度为O(n3)。因此,本文模型比文献[15]模型运算更加快速,计算复杂度更低。

由于局部梯度下降法利用负梯度作为每次迭代的搜索方向,每次以松弛解为起点,沿着目标函数在起点处的负梯度方向改善松弛解,使之接近最优解,从而提高定位精度。因此,局部梯度下降法可以有效改善求解问题的松弛解,提高定位精度。

3 实验结果与分析

为了验证算法的性能,将本文算法与文献[15]的算法进行比较实验。实验平台:Windows XP SP3+MATLAB 2009a。实验场景:2-D平面内L×L的区域随机分布100个未知节点。实验参数:一个移动锚节点按文献[15]的移动路径在网络中移动并以两级发射功率发送信标信号,如图2所示,锚节点两级发射功率对应的最大传输半径分别为r和R,r=0.15L,R=2r,锚节点移动步长s=0.1L;ε=0.01,η=0.005L。

采用归一化平均定位误差来评估算法的性能:

(12)

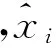
3.1 理想传输模型的定位

本实验主要比较两种方法在理想传输模型下的性能。

在实验场景中随机部署100个未知节点,分别用文献[15]的方法和本文方法进行定位,定位结果如图3所示,图中星号表示实际坐标,圆圈表示估计坐标,两者之间的连线表示定位误差。表1为实验场景随机部署100次并分别用两种方法进行定位的归一化定位误差。

图3 理想传输模型的定位结果

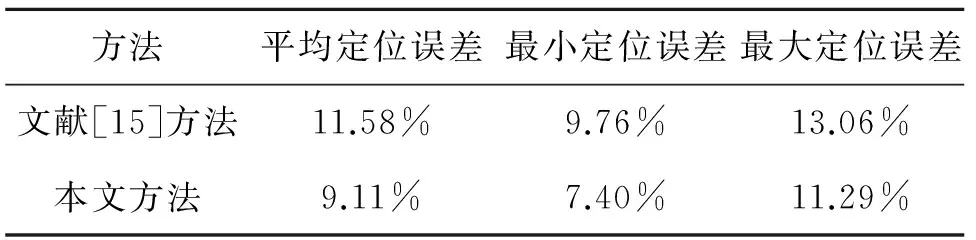
表1 理想传输模型的归一化定位误差

从图3和表1可以看出,在理想传输模型下,文献[15]取得了较高的定位精度,但由于文献[15]只利用松弛方法对凸规划问题进行求解,并没有考虑松弛解的因素;而本文采用松弛方法使得凸规划问题的可行域更大,能有效减少松弛解的数目,并且采用局部梯度下降法提高松弛解的精度,可以更有效地逼近全局最优解。因此,本文方法的定位精度比文献[15]有了一定的提高。

3.2 非理想传输模型的定位

在实际环境中,由于网络环境的复杂性及信号传播媒介等原因,锚节点传输过程的通信范围并不满足固定的无线电射程。本实验主要比较两种方法在非理想传输模型下的性能。通过不规则信号模型来模拟实际环境,利用不规则度DOI(Degree of Irregular)来表征锚节点传播信号在传输过程中受到的影响。通常,DOI为0时表示锚节点通信范围为理想的圆形区域,DOI为0.2表示节点的有效传输半径在[0.8r,1.2r]的范围内变化,DOI越大,锚节点的通信范围变化越大且越不规则。

在实验场景中随机部署100个未知节点,并在DOI=0.2时分别用文献[15]的方法和本文方法进行定位,定位结果如图4所示。

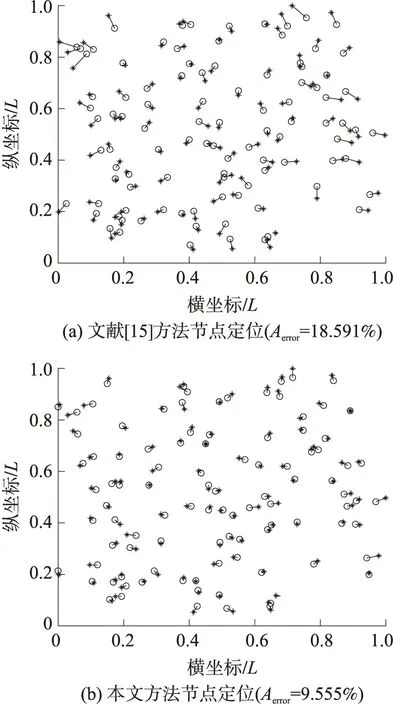
图4 非理想传输模型的定位结果(DOI=0.2)

图5 非理想传输模型的平均定位性能

由图4可知,在DOI为0.2时,本文的归一化平均误差比文献[15]提高了9.036%。

图5为实验场景随机部署100次并在不同DOI取值时,分别用两种方法进行定位的归一化定位误差。

从图5可以看出,DOI值越小,平均定位性能越接近理想传输模型的平均定位性能,但是随着DOI值的增大,定位误差也随之增长。由于本文方法在求解凸规划问题的基础上,对松弛解采用局部梯度下降法进行迭代逼近最优解,可以更好地适应实际的网络环境,故在相同的条件下,本文的平均定位性能优于文献[15]的定位性能。

3.3 不同锚节点传输半径的定位

本实验主要比较两种方法在锚节点移动步长s=0.1L的条件下,锚节点最大传输半径r分别取0.10L、0.15L、0.20L、0.25L、0.30L和0.35L时的性能。实验结果如图6所示。

图6 不同锚节点传输半径的定位性能

从图6可以看出,在锚节点移动步长相同、锚节点最大传输半径取不同值时,本文方法通过局部梯度下降法,可有效改善松弛解,其平均定位性能优于文献[15]的定位性能。

3.4 未知节点密度对定位性能的影响

本实验主要比较未知节点密度对两种方法性能的影响。在实验场景中分别随机部署25、50、75、100、125、150、175、200、225、250、275和300个未知节点,分别用文献[15]的方法和本文方法进行定位,实验结果如图7所示。

从图7可以看出,两种方法在不同未知节点密度的定位性能均较平稳,但本文方法在不同未知节点密度下的定位性能均优于文献[15],因此,本文方法可以更好地适应于不同的网络规模。

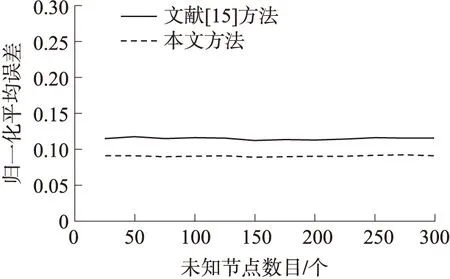
图7 不同未知节点密度的定位性能

4 结束语

针对移动锚节点凸规划定位算法的不足,提出了一种改进的移动锚节点凸规划定位算法。改进算法从求解优化问题的计算复杂度和求解精度两个方面对原算法作了改进,并在理想传输模型、非理想传输模型、不同锚节点传输半径以及未知节点密度的实验场景中进行了算法性能比较实验。实验结果表明,改进算法的定位精度和网络适应性均优于原算法,从而验证了改进措施的有效性。

[1] Akyildiz I F,Su W,Sankarasubramaniam Y,et al. Wireless Sensor Networks:A Survey[J]. Computer Networks,2002,38(4):393-422.

[2]王福豹,史龙,任丰原. 无线传感器网络中的自身定位系统和算法[J]. 软件学报,2005,16(5):857-868.

[3]Park J W,Park D H,Lee C. Angle and Ranging Based Localization Method for Ad Hoc Network[J]. The Journal of Supercomputing,2013,64(2):507-521.

[4]梅举,陈涤,辛玲. 基于蒙特卡洛方法的移动传感网节点定位优化算法[J]. 传感技术学报,2013,26(5):689-694.

[5]Ma D,Er M J,Wang B,et al. Range-Free Wireless Sensor Networks Localization Based on Hop-Count Quantization[J]. Telecommunication Systems,2012,50(3):199-213.

[6]黄亮,王福豹,段渭军,等. 基于距离重构的无线传感器网络多维定标定位算法[J]. 传感技术学报,2013,26(9):1284-1287.

[7]Chiu W Y,Chen B S,Yang C Y. Robust Relative Location Estimation in Wireless Sensor Networks with Inexact Position Problems[J]. IEEE Transactions on Mobile Computing,2012,11(6):935-946.

[8]Ji S,Sze K F,Zhou Z,et al. Beyond Convex Relaxation:a Polynomial-Time Non-Convex Optimization Approach to Network Localization[C]//Proceedings of IEEE International Conference on Computer Communications(INFOCOM),Turin,Italy:IEEE,2013:2499-2507.

[9]Doherty L,El Ghaoui L. Convex Position Estimation in Wireless Sensor Networks[C]//Proceedings of IEEE International Conference on Computer Communications(INFOCOM). Anchorage USA:IEEE. 2001,3:1655-1663.

[10]Srirangarajan S,Tewfik A H,Luo Z Q. Distributed Sensor Network Localization Using SOCP Relaxation[J]. IEEE Transactions on Wireless Communications,2008,7(12):4886-4895.

[11]Xie S,Wang J,Hu A,et al. Localization Algorithm Based on Positive Semi-Definite Programming in Wireless Sensor Networks[J]. International Journal of Signal Processing,Image Processing and Pattern Recognition,2013,6(1):1-12.

[12]Vaghefi R M,Gholami M R,Buehrer R M,et al. Cooperative Received Signal Strength-Based Sensor Localization with Unknown Transmit Powers[J]. IEEE Transactions on Signal Processing 2013,61(6):1389-1403.

[13]Liu W,Sun D,Ren P,et al. Co-SRL:A Convex Optimization Algorithm for Anchor Localization in Wireless Sensor Networks[C]//Proceedings of 2013 AASRI Conference on Parallel and Distributed Computing and Systems,Singapore,2013,5:62-66.

[14]何国钢,邓平. 一种高斯噪声下基于最大分散度的WSN半定规划定位算法[J]. 传感技术学报,2012,25(8):1116-1120.

[15]史清江,何晨. 多功率移动锚节点辅助的分布式节点定位方法[J]. 通信学报,2009,30(10):8-13.

[16]Biswas P,Ye Y. Semidefinite Programming for Ad Hoc Wireless Sensor Network Localization[C]//Proceedings of the 3rd International Symposium on Information Processing in Sensor Networks. ACM,2004:46-54.

任克强(1959-),男,教授,硕士研究生导师,主要研究方向为嵌入式系统、无线传感器网络等,jxrenkeqiang@163.com;

庄放望(1988-),男,硕士研究生,主要研究方向为无线传感器网络。

ResearchandImprovementofMobileAnchorNodeLocalizationAlgorithmBasedonConvexProgramming

RENKeqiang*,ZHUANGFangwang

(School of Information Engineering,Jiangxi University of Science and Technology,Ganzhou Jiangxi 341000,China)

In order to enhance the node localization accuracy in wireless sensor networks,this article had studied the related references,and proposed an improved convex programming localization algorithm of mobile anchor node. The algorithm made some improvements on the original algorithm to reduce the computational complexity of solving optimization problems,positive semidefinite relaxation method was utilized for enlarging the feasible region of solving problems to improve the accuracy of solving optimization problems and local gradient descent method was used to approximate the optimal estimate. The experimental results show that the algorithm has higher positioning accuracy than the original algorithm,and can better adapt to the different network scale.

wireless sensor network;localization algorithm;convex optimization;gradient descent method;mobile anchor node

2014-06-28修改日期:2014-08-26

10.3969/j.issn.1004-1699.2014.10.019

TP393

:A

:1004-1699(2014)10-1406-06