基于带电直导线周围磁场的磁传感器动静态特性标定方法

赖正喜,张晓明,2*,杨国欢,赵代弟

(1.中北大学仪器与电子学院,太原 030051;2.中北大学电子测试技术重点实验室,太原 030051)



基于带电直导线周围磁场的磁传感器动静态特性标定方法

赖正喜1,张晓明1,2*,杨国欢1,赵代弟1

(1.中北大学仪器与电子学院,太原 030051;2.中北大学电子测试技术重点实验室,太原 030051)

目前磁传感器多用于对静态或准静态磁场环境的测试,当被测磁场矢量快速变化时,磁传感器的动态特性成为影响其测量精度的关键因素。针对测试现场环境中难于产生标准的高频交变激励磁场源致使磁传感器动态特性无法准确快速标定的难题,提出一种基于带电直导线周围磁场的磁传感器动静态特性现场快速标定方法。首先提出并构建了一种基于带电直导线的标准宽频带磁场发生器,采用毕奥-萨伐尔定律分析了带电直导线周围磁场分布规律;其次通过在长直导线中加载典型交变激励电流,产生典型交变磁场,采用系统辨识方法实现对磁传感器动态特性标定;最后对某矢量磁传感器测量系统进行了时域、频域动态模型标定。实验表明所提出的磁传感器动态模型标定方法具有简便、快速、高效、准确的优点,便于工业现场对各类磁传感器进行动静态特性标定。

磁传感器;高频标准磁场源;动态特性;标定方法

在高频磁场的探测领域中,磁传感器的动态特性决定了探测精度,而准确标定磁传感器的动态特性是关键问题。例如,文献[1]提出基于磁矢量的高旋弹姿态解算是在磁传感器动态响应范围内进行高精度转速提取算法研究。文献[2-4]中提出的基于椭球约束的最小二乘法拟合是在静态或者准静态的条件下标定磁传感器的特性,它对器件所处的标定位置、旋转方式要求较高,且不能用于动态特性的标定。文献[5]借助地磁场为激励的条件下对三轴磁阻传感器参数进行了高效的标定,但它用于低速、低频的导航系统中。文献[6]新颖地采用机械臂自动标定加速度计、磁传感器的灵敏度、零点等参数,整体上提高了标定效率,但仍属于静态范畴的标定。

动态标定的目的是确定其动态指标,主要是时间常数、固有频率、动态灵敏度和阻尼比等。目前采用通电线圈标定装置的方法不能产生高频交变激励源进而不能准确的标定磁传感器的动态特性。本文首先提出一种基于带电长直导线周围产生的磁场、磁屏蔽筒等组成的标定装置产生具有宽频带高频特性的激励磁场的方法;其次,分析了动态标定的阶跃响应法、正弦响应法的原理;最后以矢量磁阻磁传感器为实验对象从时域、频域两方面动态建模对比,模型的重合度高。结果表明,本文提出的宽频带高频磁场产生方法具有设备简单、操作容易、能够保证磁传感器动态特性建模数据的可靠性等优点。

1 高频磁场产生方法

为了标定磁传感器的动态特性需要获得宽频带、高频率的输入激励磁场和输出响应数据。现有的方案是将待标定的磁传感器置于带电线圈内,通过电磁感应产生磁传感器输入所需的激励磁场,但随着电流信号频率增加,线圈电感特性将按照非线性特性明显增强,使致线圈内电流迅速减小,最终电流产生的感应磁场强度将减小,所以此方案只能标定磁传感器的静态或准静态特性,而无法满足动态特性标定的要求。为了获得频带宽、幅值恒定的高频标准激励磁场源,完成对磁传感器的动静态特性准确标定。本文设计如图1所示的高频磁场产生装置。

此高频磁场产生装置是将长直导线置于能够屏蔽地磁场、仪器设备磁场等干扰场的磁屏蔽筒内中心轴上。磁屏蔽筒是由坡莫合金、镍铁合金等具有高磁导率的多层封闭壳体材料嵌套而成。长直导线与限流电阻R串联后连接到信号源产生设备。其中,r为待标定的磁传感器与载流长直导线的垂直距离,I(t)为长直导线电流。本装置不会出现因电感特性带来的磁场衰减现象。最后通过改变电流I(t)的类型就能改变磁屏蔽筒内磁场的类型。

选取磁屏蔽筒长度L的1/2处为坐标原点,筒轴向为X轴,筒半径方向为Y轴,建立如图2所示的空间坐标系,由于磁屏蔽筒是关于坐标系轴对称,因此任意半径方向建立的Y轴不会影响对空间磁感应强度的分析。

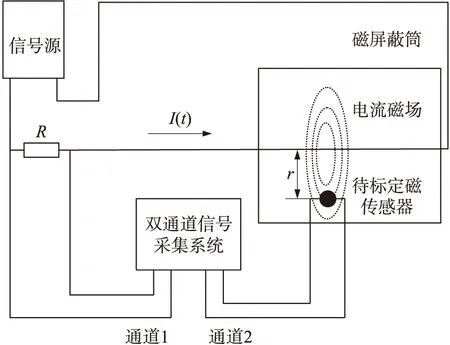
图1 高频磁场产生装置

图2 磁屏蔽筒空间坐标系

由毕奥-萨伐尔定律得载流长直导线在空间中的磁感应强度:

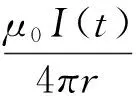
(1)

式中:真空磁导率μ0=4π×10-7N/A-2;I(t)表示长直导线的负载电流;r表示磁传感器与载流长直导线的垂直距离;θ1、θ2分别表示磁传感器与磁屏蔽筒中心轴之间的夹角,且满足如下关系:

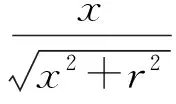
(2)

式中:L表示磁屏蔽筒的长度;x表示筒中心轴线上任意位置距离坐标原点的距离。理论分析,当L、x、r已知,电流I(t)与磁感应强度B(t)呈线性关系,可知此高频磁场产生装置能够产生磁传感器输入激励所需的宽频带高频标准磁场。

根据式(1)、式(2)得磁屏蔽筒内任意空间位置的磁感应强度:

(3)

由式(3)设高频磁场产生装置的磁屏蔽筒长L=0.5 m、半径R=0.2 m、长直导线负载电流I(t)=0.1 A。则x、r、B(t)为二元函数关系B(t)=f(x,r)。绘制磁屏蔽筒内空间位置的三维磁感应强度分布如图3所示。

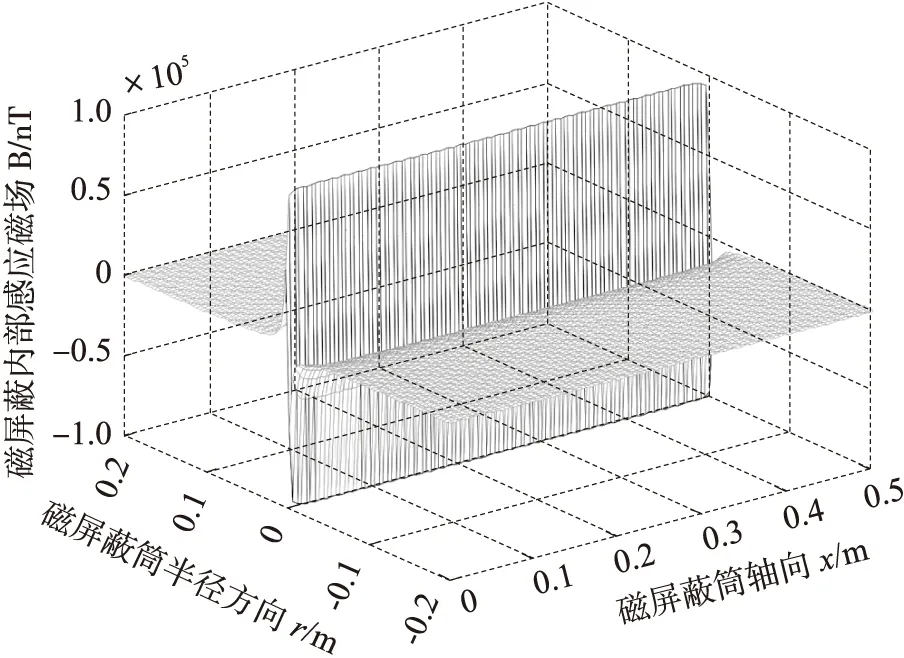
图3 三维空间磁感应强度示意图

根据上图磁场在空间中的分布规律得出:磁屏蔽筒中央(L/2)、且越靠近长直导线(r→0)处的感应磁场强度越强。此装置在高频电流信号的条件下不会出现载流长直导线电感特性带来的磁感应强度减弱现象。为了避免磁屏蔽筒对其内部磁场的聚磁效应,磁传感器与长直导线的垂直距离尽可能小于磁屏蔽筒直径的0.1倍。最后通过改变电流I(t)类型,比如,阶跃电信号、正弦电信号、随机电信号和脉冲电信号,能高效准确的获得同类型具有宽频带高频特性的激励磁场源。

2 静动态标定原理

2.1 静态标定

式(3)中,常数μ0已知,I(t)、L、x均可直接测量得到,而磁传感器与载流长直导线的垂直距离r,实则指磁传感器的矢量敏感单元与长直导线之间距离。它是无法通过外部仪器直接测量,可采用静态电流测试法,即给长直导线加载已知直流电流信号,即I(t)为常数。磁传感器输出即为长直导线r处的磁场所对应的电压信号,对式(3)反解,即可求得r。

根据磁传感器量程改变电流I(t)大小,记录已知距离r测试点处的输入磁感应强度B(t)、待标定磁传感器的输出电压y(t);按照上述过程进行多次反复测试,将得到输入输出测试数据。对输入输出数据线性或非线性拟合得出:灵敏度、零位和线性度等静态参数。

2.2 动态时域标定

磁传感器的动态特性[7]可以通过器件的传递函数来反应。由信号与系统理论,系统冲击响应的拉普拉斯变换即为系统传递函数,而实际应用中无法直接获得冲击信号[8]。时域分析中,阶跃响应为冲击响应与阶跃信号的卷积:

y(t)=h(t)*u(t)

(4)

对式(4)Laplace变换得:

Y(s)=H(s)*U(s)

(5)

待标定的磁传感器系统动态方程为:

(6)

其中,f(t)、y(t)分别表示系统输入的阶跃激励和输出的阶跃响应;n表示系统的阶次,一般n≥m。为了简化计算对动态方程式(6)两边Laplace变换:

(7)

系统输出量的Laplace变换Y(s)与输入量的Laplace变换F(s)之比为传递函数H(s)。

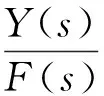
(8)

设待标定的磁传感器近似为典型二阶系统,则式(8)传递函数化为:

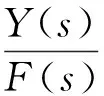
(9)

式中:ωn表示系统固有频率;ξ表示系统阻尼比;K表示静态灵敏度。阶跃信号的Laplace变换为:

U(s)=m/s

(10)

其中m表示阶跃激励磁场的幅值。根据式(5)、式(9)、式(10)联立得系统阶跃响应为:

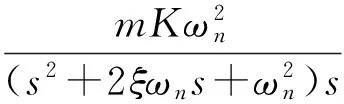
(11)

式(11)进行拉氏反变换得时域阶跃响应输出模型为:

y(t)=L-1[Y(s)]

(12)

根据阻尼比ξ的不同二阶系统阶跃响应模型y(t)不同。可对实际响应曲线用不同的模型进行系统辨识[9-11]来获得表征动态特性的参数,例如,上升时间tr,响应时间ts,超调量σp,衰减度φ等。最终确定式(9)传递函数。

2.3 动态频域标定

上述标定原理是基于时域中的阶跃响应法得出系统传递函数。为了验证标定的正确性,采用频域标定中的正弦响应法进行动态标定。

由式(9)可知,稳定状态下系统输入的正弦扫频激励与系统输出响应之间的关系即能表征系统的动态特性。

(13)

式(13)正弦扫频激励下系统的输出幅值与扫频幅值之比为|H(jω)|与角频率ω的关系即为系统的幅频特性;正弦扫频激励下系统的输出相位与扫频相位之差为φ(ω)与角频率ω的关系即为系统的相频特性。采用系统辨识理论[12-14],拟合特性曲线参数,获得系统的阻尼比、固有频率,最终确定其对被测磁信号幅值衰减、相位滞后程度。

3 实验验证

在图1高频磁场产生装置原理基础上,实验中使用函数发生器作为信号源设备、双通道示波器作为双通道信号采集系统、限流电阻R=100 Ω、选用某矢量磁阻传感器与调理电路集成系统作为待标定矢量磁传感器,如图4所示。

图4 某矢量磁阻传感器与调理电路

信号源提供5 V直流电压,采用静态电流测试法,矢量磁传感器矢量敏感单元与长直导线之间距离为r=0.51 cm。

3.1 时域建模实验

实验中采用方波电压源在长直导线中的电流产生的感应磁场作为阶跃信号,其幅值5 V、频率为500 Hz。

使用双通道示波器分别采集图1中限流电阻R两端阶跃电压信号、矢量磁传感器的X轴阶跃响应电压,如图5。将限流电阻R两端阶跃电压值补偿成磁场值,由式(3)可计算得阶跃激励磁场的幅值m=8×103nT。

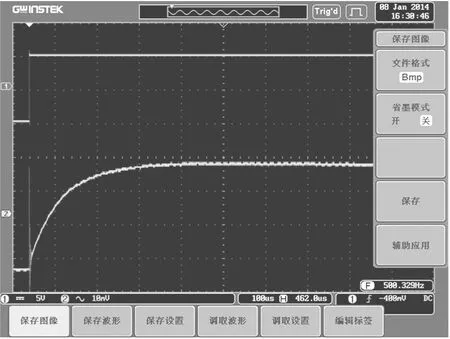
图5 矢量磁传感器阶跃响应曲线

由上图可将矢量磁传感器近似为典型一阶系统,由式(8)设其传递函数:

H(s)=K/(Ts+1)

(14)

其中,K表示静态灵敏度、T表示时间常数。系统的输出为:

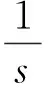
(15)

即系统的阶跃响应输出为:

Y(t)=L-1[Y(s)]=K(1-e-t/T)

(16)

其中K、T为待求参数。对式(16)采用最小二乘系统辨识法获取阶跃响应曲线,完成求解模型参数K、T。拟合出阶跃响应模型如图6所示。

图6 时域曲线拟合

拟合参数T=7.805×10-5s、K=26.28 mV/nT,其置信区间分别为(7.794×10-5,7.816×10-5)、(26.27,26.28)。由式(5)得传递函数为:

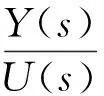
(17)

待标定磁传感器的时间常数T=7.805×10-5s、静态增益K=3.285×10-3mV/nT。

3.2 频域建模实验

对矢量磁传感器施加正弦激励x(t)=A0sin(ωt),当输出达到稳定后,双通道示波器存储输入电压、输出电压,并逐点改变电压源信号的频率,对实验数据预处理后如表1所示。

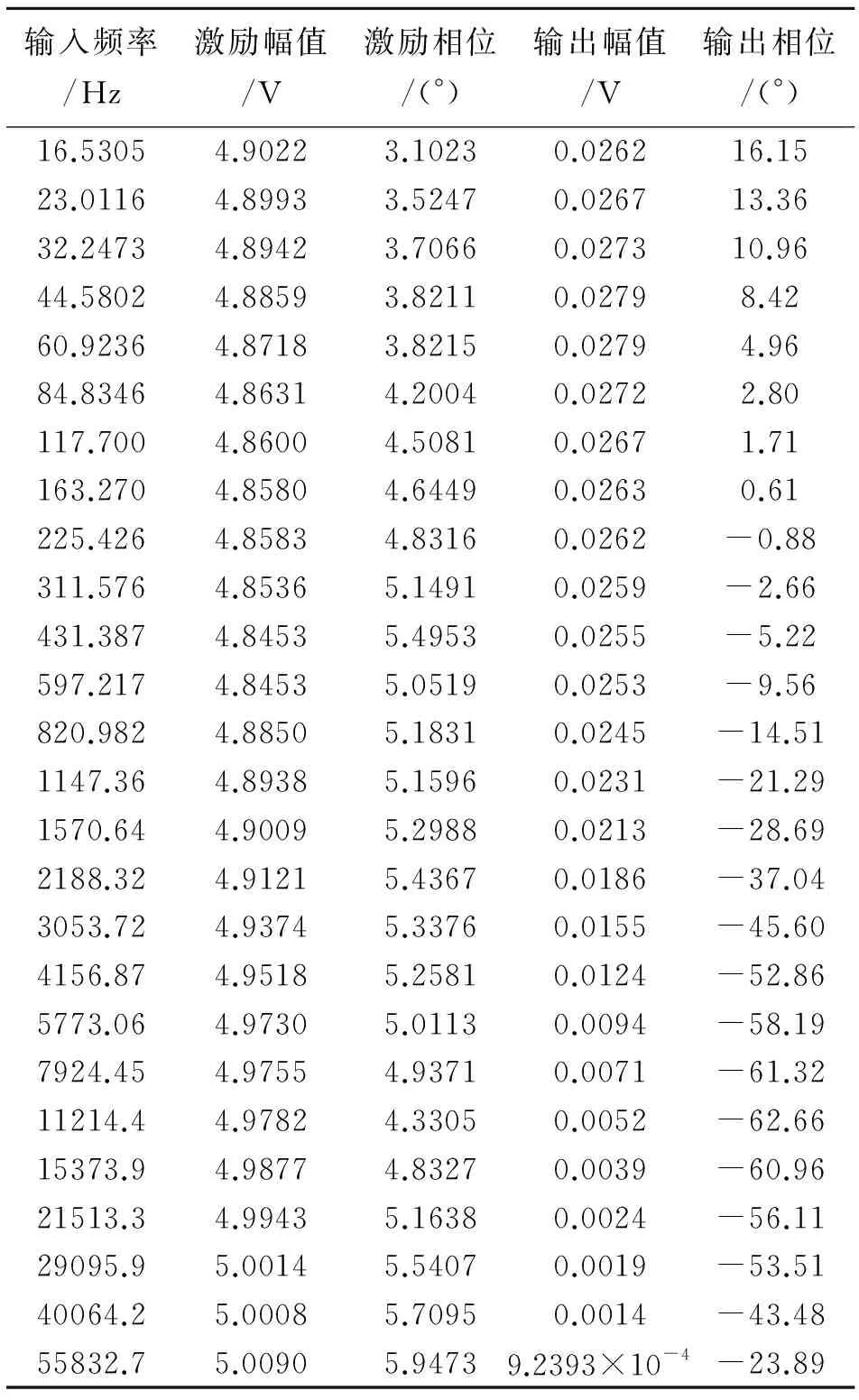
表1 输入输出数据

将输入电压数据补偿成磁场。按照频域标定理论,对实测数据预处理后,采用描点法绘制如图7中点线幅频、相频特性曲线。

由图7可知矢量磁传感器近似为典型一阶系统,由式(8)设其传递函数为:

H(s)=k/(τs+1)

(18)

其中,k表示静态灵敏度、τ表示时间常数。系统的频率特性为:

H(jω)=k/(τjω+1)

(19)

即系统的幅频、相频特性分别为:

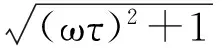
(20)

φ(ω)=arctan(-ωτ)

(21)

其中k、τ为待求参数。对式(20)采用最小二乘系统辨识法拟合参数静态增益k=3.462×10-3mV/nT、τ=7.736×10-5s,其置信区间分别为(0.003389,0.003534)、(7.463×10-5,8.009×10-5),拟合结果如图8所示。

图7 幅频与相频特性曲

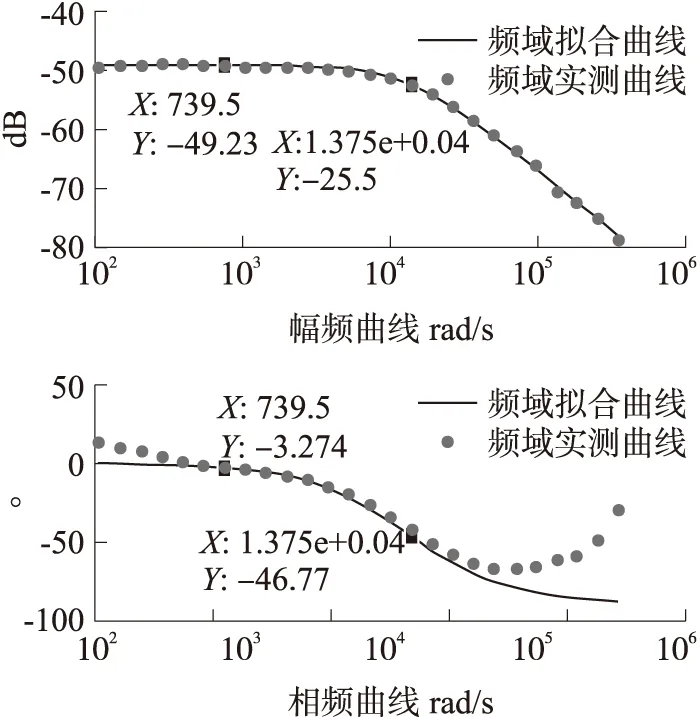
图8 频域曲线拟合

由图8可得出采用时域建模标定和频域建模标定两种手段获得的时间常数和静态灵敏度重复性高,矢量磁阻传感器与调理电路集成系统的时间常数近似为7.463×10-5s(亦即带宽约为13kHz)、静态增益为3.389×10-3mV/nT、在其带宽内相位延迟最大46.77°。

4 结论

通过一系列的实验验证:本文提出的高频磁场产生装置能够完成对矢量磁传感器的动静态标定,且标定操作具有高效、简易的特点。此高频激励磁场产生装置不仅可以用于一阶特性矢量磁传感器的动态特性研究,对于更高阶的矢量磁传感器,可通过改变激励信号类型、不同的系统辨识方法标定其动静态特性。

[1] 尚剑宇,张晓明,黄建林,等. 常规弹药转速测量时频分析方法研究[J]. 传感技术学报,2012,25(7):951-956.

[2]Bonnet S,Bassompierre C,Godin C,et al. Calibration Methods for Inertial and Magnetic Sensors[J]. Sensors and Actuators A:Physical,2009,156(2):302-311.

[3]陈国彬. 弹载三轴磁测系统设计与误差标定补偿技术研究[D]. 中北大学,2012.

[4]范玉宝,李杰,张晓明,等. 基于椭球拟合的微惯性测量组合现场快速标定方法[J]. 传感技术学报,2012,24(11):1547-1550.

[6]Renk E L,Rizzo M,Collins W,et al. Calibrating a Triaxial Accelerometer-Magnetometer-Using Robotic Actuation for Sensor Reorientation during Data Collection[J]. Control Systems,IEEE,2005,25(6):86-95.

[7]赵微微. 传感器动态特性研究[D]. 南京:南京信息工程大学,2012.

[8]程山英. 传感器动态建模算法的仿真研究[J]. 计算机仿真,2012,29(10):140-142.

[9]张文娜,叶湘滨. 基于MATLAB的传感器动态数学模型辨识系统[J]. 自动化与仪表,2002,17(5):50-52.

[10]郑剑翔. 一阶惯性延时系统的免分析建模法——MATLAB在大林算法建模仿真中的应用[J]. 福州大学学报(自然科学版),2007,35(1):64-69.

[11]强明辉,张京娥. 基于MATLAB的递推最小二乘法辨识与仿真[J]. 自动化与仪器仪表,2008(6):4-5.

[12]吕秋霞,李继容. MATLAB在系统辨识中的应用[J]. 仪器仪表用户,2008,15(1):60-61.

[13]Rupnik K,Kutin J,Bajsi I. Identification and Prediction of the Dynamic Properties of Resistance Temperature Sensors[J]. Sensors and Actuators A:Physical,2013,197:69-75.

[14]贾小勇,徐传胜,白欣. 最小二乘法的创立及其思想方法[J]. 西北大学学报(自然科学版),2006,36(3):507-511.

赖正喜(1988-),男,汉族,四川三台人,中北大学硕士研究生,主要研究方向为组合导航技术与电路系统设计,523411674@qq.com;

张晓明(1976-),男,汉族,山西新绛人,副教授,硕士生导师,现在中北大学仪器科学与动态测试教育部重点实验室工作,主要研究方向为动态测试及组合导航,zxm_auto@nuc.edu.cn。

CalibrationMethodBasedontheMagneticFieldAroundtheWireElectricStraightStaticandDynamicPropertiesofMagneticSensors

LAIZhengxi1,ZHANGXiaoming1,2*,YANGGuohuan1,ZHAODaidi1

(1.Instruments and Electronic Engineering,North University,Taiyuan 030051,China;2.Key Laboratory for Electronic Measurement Technology,North University,Taiyuan 030051,China)

Currently magnetic sensors used for static or quasi-static magnetic field of environmental measuring,when rapid changes in the measured magnetic field vector,the dynamic characteristics of the magnetic sensor is a key factor affecting the measurement accuracy. For the test site environment is difficult to generate a standard high-frequency alternating magnetic field excitation source causing the dynamic characteristics of the magnetic sensor calibration problem can not be quickly and accurately,this paper presents a magnetic sensor based on the magnetic field around a straight wire electrified static and dynamic characteristics of rapid field calibration method. The article first proposed and constructed a standards based wideband charged straight wire magnetic field generator,using the Biot-Savart law analysis of the distribution of the magnetic field around a charged straight wire;followed by loading the typical alternating excitation current in long straight wire,typical alternating magnetic field was produced. The dynamic characteristics of the magnetic sensor was calibrated by using system identification methods;Finally,a vector magnetic sensor measurement system in time domain,frequency domain dynamic model calibration. Experimental results show that the proposed dynamic model of the magnetic sensor calibration method is simple,rapid,efficient and accurate advantages of various types of industrial site to facilitate static and dynamic characteristics of the magnetic sensor calibration.

magnetic sensor;high frequency standard magnetic field source;dynamic characteristic;calibration method

2014-06-09修改日期:2014-08-27

10.3969/j.issn.1004-1699.2014.10.008

V241.61.1

:A

:1004-1699(2014)10-1343-06