重型卡车驾驶室结构噪声预测与板件声学贡献度分析

张志勇，张义波，刘 鑫，谢小平

(1. 长沙理工大学 汽车与机械工程学院，长沙 410004；2. 湖南大学 汽车车身先进设计制造国家重点实验室，长沙 410082)

随着现代汽车工业技术的飞速发展，人们对乘坐的舒适性要求越来越高，特别是声学舒适性要求。汽车车内噪声不但增加驾驶员和乘客的疲劳程度，而且影响汽车的行驶安全性。因此，驾驶室声学舒适性已成为汽车乘坐舒适性的重要评价指标之一，日益受到人们的重视[1]。

车内噪声分为空气噪声和结构噪声，其中结构噪声是噪声源或振动源作用于驾驶室壁板引起振动而辐射的噪声。结构噪声以20～200 Hz的中低频噪声为主，该频段噪声给人的主观感觉是“booming”声，它能造成车内乘员的强烈不适感。因此，如何降低驾驶室结构噪声，成为汽车设计中的一项重要挑战性任务[2]。由于重型卡车工作环境复杂多变，路面条件恶劣，行驶过程中车身结构，尤其是驾驶室在各种振动源的激励下会产生强烈振动和噪声，严重影响了驾驶员的 乘坐舒适性，极易导致驾驶疲劳和身体不适，造成错误的判断而引发事故。因此，降低重型卡车驾驶室的NVH性能具有重要的意义[3]。

以减振降噪为目的的驾驶室板件结构优化方法，通过优化板件厚和合理布置加强筋等措施改善板件的振动特性，降低振动幅值而改善驾驶室的声学舒适性。然而，驾驶室各板件对于驾驶室内任意位置的声压贡献并非一致。因此，在结构优化之前有必要进行板件声学贡献度分析，以确定对驾驶室内噪声影响最大的结构板件，从而实现有针对性的结构优化，这是进行驾驶室低噪声结构优化设计的重要环节和有效手段[4]。

本文首先建立了重型卡车驾驶室白车身有限元模型，分别进行了计算模态和试验模态对比分析，不仅获得了驾驶室主要板件的动态特性，而且验证了有限元模型的准确性；然后通过声-固耦合系统的模态分析和驾驶员耳旁噪声预测，获得结构与声腔的耦合关系，并进一步验证了有限元模型的准确性；最后基于声-固耦合模型进行板件贡献度分析，找到了对驾驶室内峰值声压贡献最大的板件和主要的结构参与模态，并通过对比分析板件厚度优化前后的噪声声压，验证了分析结果的正确性。

1 驾驶室声-耦合系统建模与分析

1.1 驾驶室有限元建模与精度验证

以国内某重型卡车驾驶室为研究对象，利用UG软件建立包含146个部件的驾驶室三维模型。采用壳单元建立驾驶室有限元模型，设置网格大小为10 mm，材料密度为7.8 g·cm-3，弹性模量为2.1×105MPa，泊松比为0.3，得到含有331 741个四边形单元、13 604个三角形单元和10 917个焊点单元的白车身有限元模型，如图1(a)所示。在MSC.Nastran软件中采用Lanczos法精确计算白车身结构的自由模态。经计算得到的驾驶室前8阶自由模态的频率和振型描述如表1所示。

图1 驾驶室分析有限元模型

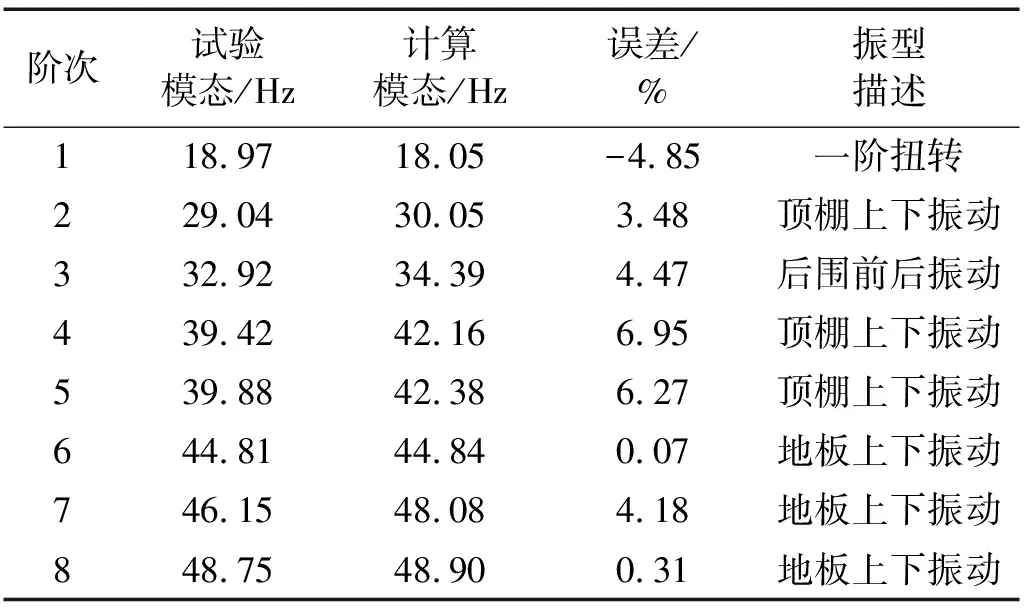
表1 计算模态与试验模态对比

为了确保有限元模型能准确反映实际对象的振动特性，常通过对比分析计算模态和试验模态来验证有限元模型的精度和分析结构振动与噪声声压的关系[5]。在进行白车身试验模态时，将重型卡车的驾驶室白车身用弹性软垫支撑，近似模拟自由状态；然后通过电磁激振器产生激励信号，采用单点激振多点拾振的方法进行试验，同时通过动态信号采集系统采集激励和响应信号；最后经过后处理提取前8阶固有频率和模态振型。

计算模态和试验模态的结果对比如表1所示。由表可知，计算模态与试验模态的固有频率误差均在10%以内，并且模态振型描述一致，因此验证了驾驶室白车身有限元模型的精度，说明本文建立的白车身有限元模型能准确反映实际结构的振动特性，可用于后续计算和分析。

1.2 声-固耦合系统建模

在驾驶室白车身有限元模型的基础上，首先建立驾驶室左右门和前后挡风玻璃，并通过适当的连接方式连接门窗系统、前后挡风玻璃等部件构成完整的车身模型；然后利用相应的工具对模型的小孔和缝隙等进行适当的填补，形成一个封闭的结构有限元模型；最后抽取驾驶室内部空腔。考虑到计算的精度和规模，采用单元长度为50 mm标准划分空腔，得到包含83 467个四面体单元的声腔有限元模型，如图1(b)所示。

驾驶室结构的振动和声腔空气的振动相耦合，会使整个驾驶室的声学特性发生改变。声学系统的声学特性和结构系统的力学特性共同决定耦合系统的声压分布。在有限元耦合算法中，通过联立结构有限元方程和声腔有限元方程建立声-固耦合系统的有限元模型。利用直接积分法或模态叠加法即可求得结构单元的位移和声腔单元的声压[6]。其中声腔声学有限元方程可表示为：

(1)

式中:Ma、Ca和Ka分别为声腔的质量矩阵、阻尼矩阵和刚度矩阵，A为结构声场耦合矩阵，Pa为空气单元节点声压向量，u为节点位移向量，ρ是空气密度。

考虑与声场耦合时，结构有限元方程为：

(2)

式中:Ms、Cs和Ks分别为结构的质量矩阵、阻尼矩阵和刚度矩阵，Fs是结构所受的外载荷向量。

联立声腔有限元方程和结构有限元方程，可得到如下的声-固耦合系统的有限元方程。

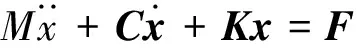
(3)

式中:

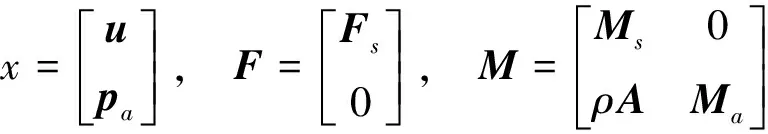
当不考虑阻尼的作用，上式可简化为：

(4)

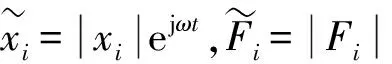
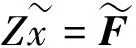
(5)

式中:Z为耦合系统的阻抗矩阵，可表示为

本文利用式(5)表示的耦合关系分析驾驶室板件振动对车内声场特性的影响，计算声-固耦合系统的模态和驾驶室内声场的声压分布，进而进行驾驶室板件声学贡献分析，确定出对场点声压影响最大的板件。

1.3 声-固耦合模态分析

在MSC.Nastran中，由声腔边界上的节点自动搜索结构节点来实现声腔和结构的耦合作用。采用复模态特征值提取法，对声-固耦合系统进行模态分析，识别耦合系统的模态频率和振型。在前100 Hz内共有43阶模态频率，前8阶模态如表2所示。

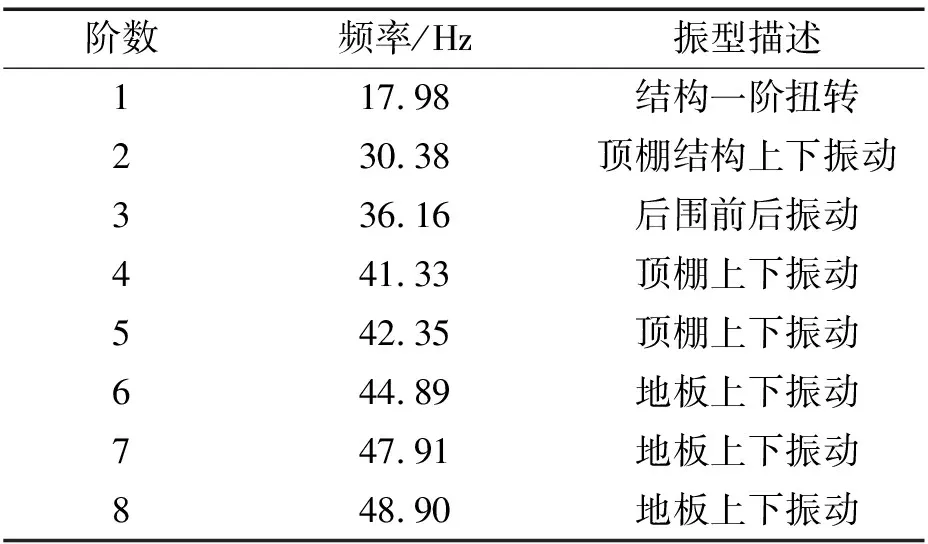
表2 耦合系统前8阶模态频率和振型描述

通过对比分析结构模态和耦合模态的计算结果，两者的模态频率基本吻合，说明耦合模态主要是由结构模态激发出来的。但由于耦合的作用，耦合模态频率稍有改变，模态阶次更为密集。另外，从模态频率上看，耦合系统的模态频率比相对应的结构模态频率要略小一些，这主要是由于驾驶室内空气的阻尼作用使得结构的模态频率减小；而且在空气流动条件下的振动模态频率，一般比自由模态的频率小。从振型描述中可以看出，结构模型和耦合模型的振型完全一致，说明本文所研究的驾驶室结构与其中的空气流体耦合作用较弱，两者的相互作用没有激发新的振动模式，简单的结构优化可能对车内噪声控制作用明显。另外，从模态振型描述可知，主要变形部位都集中在顶棚和后围上，两者应作为驾驶室低噪声结构优化对象。

2 驾驶室结构噪声预测与分析

2.1 工况试验

为了获得驾驶振动激励信号，进而对驾驶室进行噪声预测和精度检验，本文进行了重型卡车实车工况试验，采集了驾驶室4个悬置处的振动加速度和驾驶员耳旁噪声声压。试验场地选择B级柏油路面，天气良好无风，环境噪声小于被测车辆工作噪声10 dB以上。测试时被测卡车的门窗、通风进出口都关闭，刮水器、通风扇、空调均未运行。采样频率取2 000 Hz，记录时间为30 s，重复次数为3次。

试验中传感器布置如图2所示。其中振动信号采集驾驶室4个悬置点的Z方向加速度，驾驶员耳旁噪声测试方法参照文献[7]的规定进行。实车工况为空载下的60 km/h匀速工况。加速度和声压信号利用NI PXI 4472动态测数据采集卡，在LabVIEW编写的程序控制下同步采集。

图2 振动与噪声测试

2.2 驾驶室结构噪声预测与分析

由于在Virtual.lab中进行声场响应分析时，所加载的外部激励必须是力信号，因此需要将加速度载荷转换成力载荷。其中的大质量法被证明存在较大的分析误差[8]，而传递函数法需要通过试验确定悬置的传递函数，比较费时费力[9]。在本文中，利用Nastran的结构求解器加载加速度激励进行频率响应分析，直接求解悬置点节点的约束力，并作为声场响应分析的激励力信号。另外，采用直接积分法计算驾驶室内的声学响应，其中分析频率范围为20～200 Hz，步长为1 Hz。驾驶员耳旁噪声预测值和试验值对比如图3所示。

由图3可知，噪声预测值和试验值非常接近，只是在某些频率上，两者幅值存在一定的误差。其原因可能是外部的噪声干扰，或驾驶室结构模型的参数不确定性造成的。但预测值和试验值误差仍在允许的范围之内，说明本文建立的重型卡车驾驶室噪声预测模型有较高精度。另外，由图3还可观察到在35～40 Hz出现较大的声压峰值，这主要是由于发动机的二阶激振引起的；其次在100～130 Hz和160～180 Hz频段均出现了较大的声压峰值，这些频段与声腔的横向一阶、纵向一阶、横向二阶和纵向二阶振动密切相关，引起声腔共鸣而导致声压出现峰值。

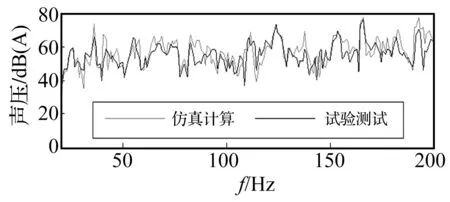
图3 驾驶室噪声预测

3 驾驶室板件贡献度分析

3.1 驾驶室板件声学贡献量分析

由噪声的产生机理可知，驾驶室内某点的声压是各个板件振动所生成的声压叠加而成。因此，可以通过板件结构优化来降低其振动幅值，从而达到降低驾驶室结构噪声的目的。然而，由于每个板件对驾驶室内的场点声压在每个频段内的贡献并非一致，因此需要通过板件声学贡献量分析，评价并确定对主要声压峰值贡献大的板件，进而对其进行结构优化，达到改善驾驶室声学舒适性的目的[4]。

如前所述，驾驶室某场点处的声压为各板件产生声压的叠加，即：

(6)

式中:p为场点总声压响应，Ai(ω)为声传递矢量，N为单元总数，ω为角频率，ve,i(ω)为单元 的法线速度。

如果第j板件共有m个单元，则由于该板件振动而在该场点处产生的声压pj表示为：

(7)

第j板件对场点总声压的声学贡献量Dj定义为该板件振动所产生的声压pj在场点总声压p上的投影，表示为：

(8)

式中:p*为p的共轭复数，Re(·)为复数的实部。

在进行板件声学贡献量分析之前，将声腔包络面按主要组成板件分成16个板块，分别为：顶棚中部1、顶棚前端2、顶棚后端3、后围4、前挡风玻璃5、仪表板6、左地板7、右地板8、地板中部9、地板后部10、左侧围上部11、左侧围12、左车门13、右侧围上部14、右侧围15、右车门16。基于已建立的声-固耦合模型，利用声腔边界表面振动速度作为板件贡献量分析的速度边界条件，提取最大和次大声压峰值下的板件贡献量，乘以归一化系数，得到如图4所示的板件声学贡献系数。

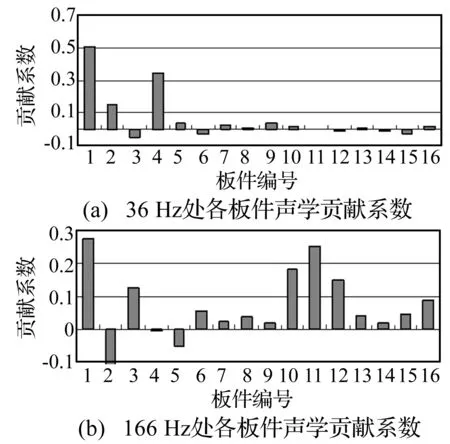
图4 16块板件对驾驶员耳旁噪声的声学贡献系数

由图4可知，对36 Hz声压峰值贡献较大的板件为顶棚中部1、顶棚前端2和后围4。对166 Hz声压峰值贡献较大的板件是顶棚中部1、顶棚后端3、地板后部10、左侧围上部11和左侧围12。值得注意的是，顶棚前端2对36 Hz声压峰值频率为正贡献，而对166 Hz声压峰值频率为负贡献，且贡献系数基本相当，因此对它的结构优化需要权衡。但是，其他板件对这两个声压峰值频率都为正贡献，在进行驾驶室结构低噪声优化时，应重点考虑这这些板件。

3.2 结构模态参与因子分析

结构模态参与因子是指每一阶结构模态对耦合系统声学响应的参与量。通过结构模态参与因子分析可以找到对耦合系统声学响应最敏感的结构模态，从而有针对性的改善驾驶室声学性能[6]。在获得结构节点振动位移和声腔节点声压的基础上，可表示为模态参与因子的函数，如：

(9)

式中:Φs和Φa分别为独立系统无阻尼时的结构模态和声腔模态，ξs和ξa分别为对应的模态参与因子。

利用式(9)可将式(3)的有限元模型转换到模态空间，从而求得结构和声腔的模态参与因子。由于高阶模态参与因子很小，在计算最大声压峰值频率166 Hz处的结构模态参与因子时，只列出前200阶模态参与因子，如图5所示。

从结构模态参与因子图中可以看出，较大的参与因子均集中在120～140阶之间。结构模态参与因子最大的两阶模态分别为130阶和126阶模态。通过查看130阶和126阶模态振型可知，这两阶模态的主要振动产生于顶棚、后围等部位。通过结构模态参与因子再次证明顶棚和后围对驾驶室的峰值噪声有较大的贡献，应作为驾驶室低噪声结构优化的对象。

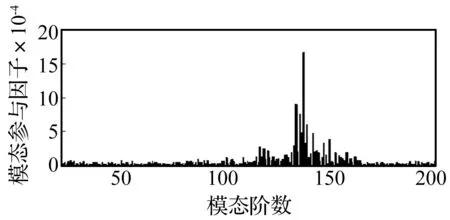
图5 166 Hz处的结构模态参与因子

3.3 分析结果验证

从板件贡献度分析结果可以看出，顶棚对驾驶员耳旁噪声声压的正贡献最大，其次是后围。从降低驾驶室噪声的角度需要对这两块板件结构进行优化。在本文中，为了验证板件贡献度分析结果的准确性，将顶棚板件厚度由1 mm增加到1.2 mm，将后围板件厚度由0.8 mm增加到1 mm。通过耦合声学有限元法计算，可得到板厚优化前后的声压曲线对比，如图6所示。从图中可以看出，进行简单的顶棚和后围结构优化后，166 Hz处出现的最大声压峰值由77.32 dB下降到了69.07 dB，降低了8.25 dB，起到了良好的降噪效果，同时也证明了板件贡献度分析的有效性。

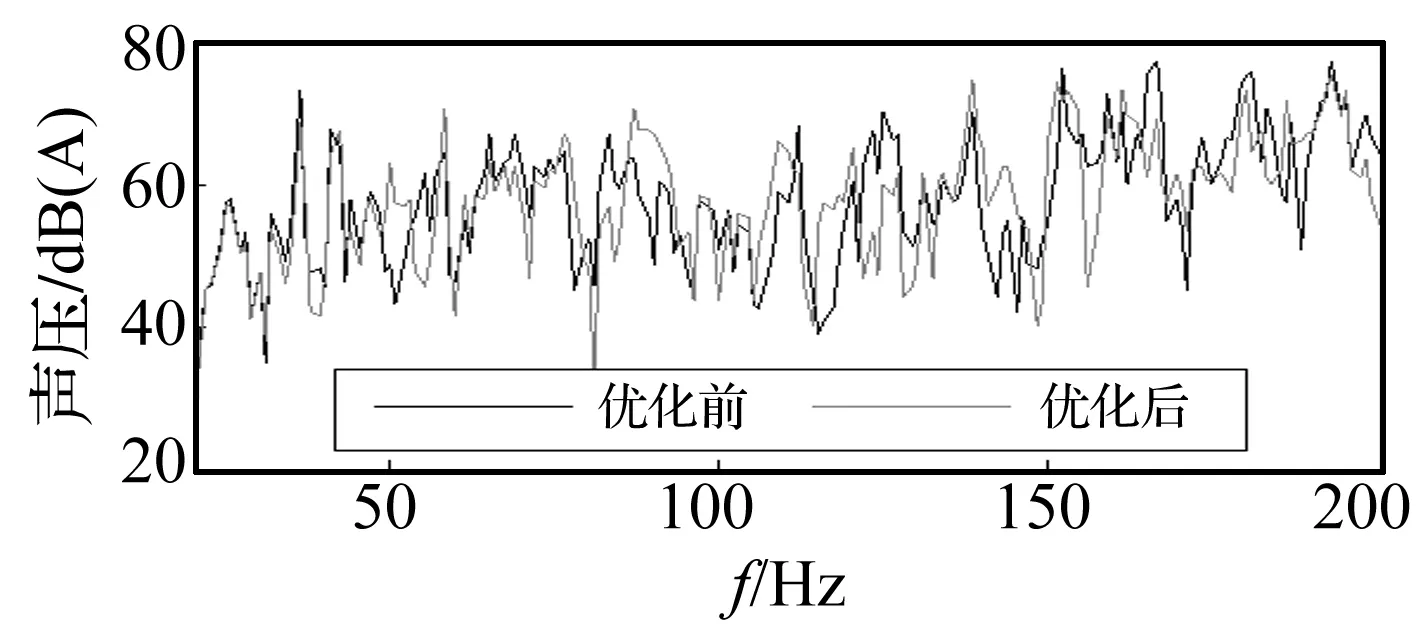
图6 优化前后驾驶员耳旁噪声声压对比

4 结 论

本文首先建立了重型卡车白车身有限元模型，通过计算模态和试验模态的对比分析，验证了有限元模型的有效性；在此基础上建立了驾驶室声-固耦合模型，对比分析了耦合模态和结构模态，确定耦合模态主要是由结构模态激发所致，且主要变形部位集中于驾驶室的顶棚和后围；利用实车工况试验所测的驾驶室悬置加速度，作为耦合系统的外部激励对驾驶员耳旁噪声进行预测。通过与试验测试噪声进行对比，进一步验证了耦合模型的精度；最后计算驾驶室16个板件对驾驶员耳旁噪声的声学贡献量，以及进行了结构模态参与因子分析，确定了驾驶室的顶棚和后围对驾驶员耳旁噪声影响最大。通过对比分析板件厚度优化前后的噪声声压，证明了该结论的正确性。

[1] 邬广铭, 史文库, 刘伟, 等. 基于模态灵敏度分析的客车车身优化[J]. 振动与冲击, 2013, 32(3): 41-45.

WU Guong-ming, SHI Wen-ku, LIU Wei, et al. Structural optimization of a light bus body-in-white based on modal sensitivity analysis[J]. Journal of Vibration and Shock, 2013, 32(3): 41-45.

[2] Han X, Guo Y J, Zhao Y E, et al. The application of power-based transfer path analysis to passenger car structure-borne noise[J]. Proceedings of the Institution of Mechanical Engineers, Part D: Journal of Automobile Engineering, 2008, 222(11): 2011-2023.

[3] Chen S, Wang D, Song J, et al. Interior noise prediction and analysis of heavy commercial vehicle cab[C]. SAE Paper: 2011-01-2241.

[4] 赵静, 周鋐, 梁映珍, 等. 车身板件振动声学贡献分析与优化[J]. 机械工程学报, 2010, 46(24): 96-100.

ZHAO Jing, ZHOU Hong, LIANG Ying-zhen, et al. Vehicle body panel acoustic contribution analysis and optimization[J]. Journal of Mechanical Engineering, 2010, 46(24): 96-100.

[5] 高云凯, 冯海星, 马芳武, 等. 基于PolyMAX的声固耦合模态试验研究[J]. 振动与冲击, 2013, 32(2): 158-163.

GAO Yun-kai, FENG Hai-xing, MA Fang-wu, et al. Acoustic-structure coupled modal test based on PolyMAX[J]. Journal of Vibration and Shock, 2013, 32(2): 158-163.

[6] 吴光强, 盛云, 方园. 基于声学灵敏度的汽车噪声声-固耦合有限元分析[J]. 机械工程学报, 2009, 45(3): 222-228.

WU Guang-qiang, SHENG Yun, FANG Yuen.Coupled acoustic-structural finite element analysis of vehicle interior noise based on acoustic sensitivity[J]. Journal of Mechanical Engineering, 2009, 45(3): 222-228.

[7] QC/T57-1993. 汽车匀速行驶车内噪声测量方法[S]. 北京: 中国汽车工业总公司, 1993.

[8] 周国良, 李小军, 刘必灯,等. 大质量法在多点激励分析中的应用误差分析与改进[J]. 工程力学, 2011, 28(1): 48-54.

ZHOU Guo-liang, LI Xiao-jun, LIU Bi-deng, et al. Error analysis and improvements of large mass method used in multi-support seismic excitation analysis[J]. Engineering Mechanics, 2011, 28(1): 48-54.

[9] Guo R, Zhang L J, Zhao J, et al. Interior structure-borne noise reduction by controlling the automotive body panel vibration[J]. Journal of Automobile Engineering, 2012, 226(7): 943-956.