均匀热环境下四边固支矩形PCB薄板的自由振动
2014-09-07黄再兴
高 军,黄再兴
(南京航空航天大学 机械结构力学及控制国家重点实验室,南京 210016)
表面贴装技术(SMT)以其成本低、集成度高、电子组件重量轻、易于自动化等优点广泛应用于微电子电路[1-2]。影响表面贴装电子产品可靠性的主要环境因素是热和振动冲击,特别是在环境振动和热载荷的复杂环境下,两类载荷共同影响贴装形式元器件的内力情况,导致振动产生的动态应力和热疲劳应力相互叠加引起封装的失效,从而影响整个封装形式可靠性与寿命。同时,这两种载荷相互间产生耦合,并非仅仅只表现为两种载荷作用的简单叠加。目前,已发现大型的工作站随工作温度升高到一定程度会产生共振,从而会影响其正常工作。明显地,这是由热环境温度的变化导致封装结构固有频率改变带来的问题。该问题涉及封装结构固有频率与环境温度的相互耦合,但目前还缺乏定量的研究。
已有学者分别对振动和热环境下表面贴装形式电子元器件的结构和可靠性进行了一些研究[3-6]。但是,由于与热循环载荷相比,振动载荷具有高频特性,两者的周期相差较远,在处理这两种载荷同时作用时具有较大的困难,所以综合考虑环境振动和热载荷共同作用下电子封装可靠性以及寿命预测的研究较少。如朱继元[7]等利用ANSYS软件,通过考虑材料参数随温度变化的因素对振动的影响来分析热和振动耦合的问题。Barker 等[8-9]提出线性叠加的方法考虑热和振动耦合载荷对可靠性的影响,分别计算振动载荷和热载荷引起的损伤,然后将两者线性叠加。邓定宇等[10]考虑温度产生的平均应力对振动损伤计算的影响,采用递增损伤累积方法计算疲劳寿命。从目前研究现状来看,并未从根本物理机制上去确定热和振动耦合作用对电子封装结构的影响。
因表面贴装的封装结构中PCB板为镶嵌于上一级封装结构,或者沿边界完全固定于其他装置中[3-6],其中PCB薄板可以认为是四边固支的矩形薄板。为此本文忽略表面贴装形式中PCB板上其他元件,将PCB板简化为四边固支矩形薄板,通过对热载下薄板自由振动的分析来确定表面贴装结构中PCB薄板的热和振动载荷的相互影响。文中基于刚性板的小挠度理论,推导了热载下矩形PCB薄板的自由振动微分方程,进而利用虚位移理论得出了四边固支矩形薄板基本频率和自由振动挠度值的计算方法。并讨论了薄板的几何尺寸、温度等对PCB薄板自由振动固有频率的影响。
1 热载下PCB薄板振动微分方程
在目前的研究中,PCB板可考虑为连续、均匀的各向同性弹性薄板,同时PCB板的变形和内力状态均认为不影响结构的热传导过程和温度场的变化。现取一尺寸为a×b×h的PCB矩形薄板进行分析,坐标如图1所示。

图1 PCB薄板模型
根据刚性板和小挠度理论的基本假设[11-12],有
u=-zw,xv=-zw,y
(1)
式中,u,v和w分别为沿x,y和z轴方向的位移。
所以薄板的几何方程为:
(2)
因不计应力分量σz引起的应变,所以热环境下薄板物理方程可写为:
(3)
式中α为材料的线膨胀系数,E为材料的弹性模量,μ为材料的泊松比,T=T(x,y,z)是薄板中任意一点的变温。由式(2)和式(3)求解应力分量得:
(4)
薄板单位宽度上的内力和内力矩可以用应力沿厚度方向积分得到:
(5)
将式(4)代入(5)得:
(6)

根据经典薄板的小挠度理论,其动力平衡方程为[13-14]:
(7)
式(7)中前两式是独立的,将式(6)代入式(7)的第三式得:
D4w+(φ,xx+φ,yy)-
N(w,xx+w,yy)+ρhw,tt=0
(8)
式中:
由于温度在面内均匀变化,则
φ,xx+φ,yy=0
(9)
将式(9)代入式(8)得:
D4w-N(w,xx+w,yy)+ρhw,tt=0
(10)
式(10)即为PCB薄板在热载作用下基于小挠度理论的自由振动微分方程。从微分方程中可以看出,热载下的薄板振动等效于面内受均布张力N的薄板振动。
2 PCB薄板热载下温度场分析
为了分析温度作用下PCB薄板的振动规律,必须确定薄板温度场的分布。PCB板表面正常工作中的电子芯片产生热量,使得薄板一侧温度升高。为简单起见认为电子芯片的热量均匀传到所在一侧的表面,表面各处的温度均相等。薄板热量从高温面传向低温面,温度仅沿厚度方向均匀线性变化。设薄板各点初始温度均相同,则热环境下薄板各点温度可表示为:
(11)
式中,T1表示上表面的变温值,T2表示下表面的变温值。
将式(11)代入式(6)第一式得,
(12)
薄板内力N表达式中负号表示当薄板温度增加时,薄板内产生压应力;当温度降低时,薄板内产生拉应力。
将式(12)代入式(10)得热载下PCB薄板自由振动微分方程:
当由于电子封装结构的工作环境整体温度升高,引起PCB薄板温度变化时,薄板上下表面变温相等,即T1=T2,此时:
N=-EαhT1
(14)
此时自由振动微分方程为:
D4w+EαhT1(w,xx+w,yy)+ρhw,tt=0
(15)
3 PCB薄板热载下自由振动
按照结构力学的方法,四边固支的薄板等效于四边为简支的基本系统,同时四条边上作用着连续分布的弯矩[15]。热载下四边固支的PCB薄板如图2(a)可等效为图2(b)所示四边简支基本系统,同时作用着均布张力和连续分布的弯矩。在y=0,y=b这两条边上作用着随各点位置x而变化的弯矩M(x),在x=0,x=a这两条边上作用着随各点位置y而变化的弯矩M(y)。
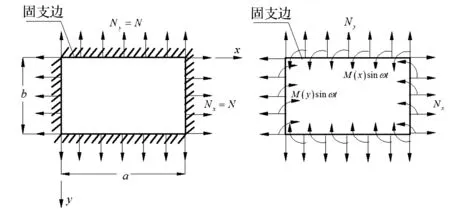
图2 四边固支PCB薄板简化模型
设薄板等效基本系统在振动时瞬时挠度[16]为:
(16)
式中,ω为薄板的自振频率,系数amn可用虚位移原理来计算。当板作对称形式的振动时,其固定边上所作用的弯矩各为M(x)sin(ωt),M(y)sin(ωt)。根据虚位移原理,当amn增为amn+δamn时,惯性力所做的功为:
(17)
沿板边界上作用的弯矩所作的功为:
(18)
式中Em和Fn分别为将弯矩M(x)和M(y)展成正弦级数时的系数,即
(19)
于是当虚位移进行时,外力所作的功为:
(20)
薄板内变形能的增量为:
sin2ωtamnδamn
(21)
由虚位移原理δU=δT得:
(22)
将式(22)代入式(16)得薄板的振动挠度为:
(23)
当薄板为正方形板时a=b,并且Nx=Ny=N,则弯矩沿四边的分布相同,于是Fn=En,则式(23)变为:
(24)
由于薄板的四边固定,有:
(25)
将式(24)代入式(25)的第一式得:
(26)
于是:
(27)

利用文献(15)附录中式(28),
(28)
方程(27)可写作,
(29)
式中,
(30)
方程(29)为一组无穷联立方程,且方程系数与薄板频率ω有关,利用齐次方程组有非零解的条件,使它的系数矩阵等于零,就可得到无穷个根,其中最小的一个根就是振动的基本频率。其中方程的个数在实际的计算中根据精度要求取有限项。将计算得到的基本频率代回方程(29)解联立方程可得Em,从而可由式(19)得到分布在固定边上的弯矩值。将Em以及基本频率代入式(24)即可计算振动中各点挠度值。
4 PCB薄板振动的影响分析
为了具体分析温度以及其他因素对热载下PCB板自由振动固有频率的影响,取文献[17]中PCB板材料以及尺寸数据进行数值计算,参数如表1所示。其中PCB板为高度1 mm边长10 mm的正方形板。

表1 PCB板材料参数

图3 薄板频率随温度变化曲线
假定电子封装结构的工作环境整体温度从室温25℃升高到125℃,即薄板变温T从0℃到100℃。通过式(14)即可计算薄板在不同的变温下引起的内力N,内力值此时为负值表示温度升高薄板内产生压应力。取方程组(29)的前四项,将内力N的值代入方程,并取这四阶系数矩阵等于零,即可得到四边固支PCB薄板在不同温度下自由振动的基本频率ω,如图3所示。
从图中可以看出,随着温度的上升,薄板基本频率近似呈线性下降。薄板内的压应力降低了薄板的抗弯能力,进而降低了薄板的固有频率。反之当温度降低时,薄板内拉应力可使得薄板的抗弯能力提高,进而提高薄板的固有频率。
通过计算薄板边长从10 mm到100 mm变化时的基本频率值,分析PCB薄板的尺寸对热载下薄板固有频率的影响。假定PCB薄板的温度从室温25℃升高到45℃,即薄板的变温T为20℃。图5所示为薄板在不同边长情况下的基本频率变化曲线。从图中可以看出,薄板的边长对基频影响很大,边长从10 mm到20 mm之间急剧下降,之后趋于平缓变化。
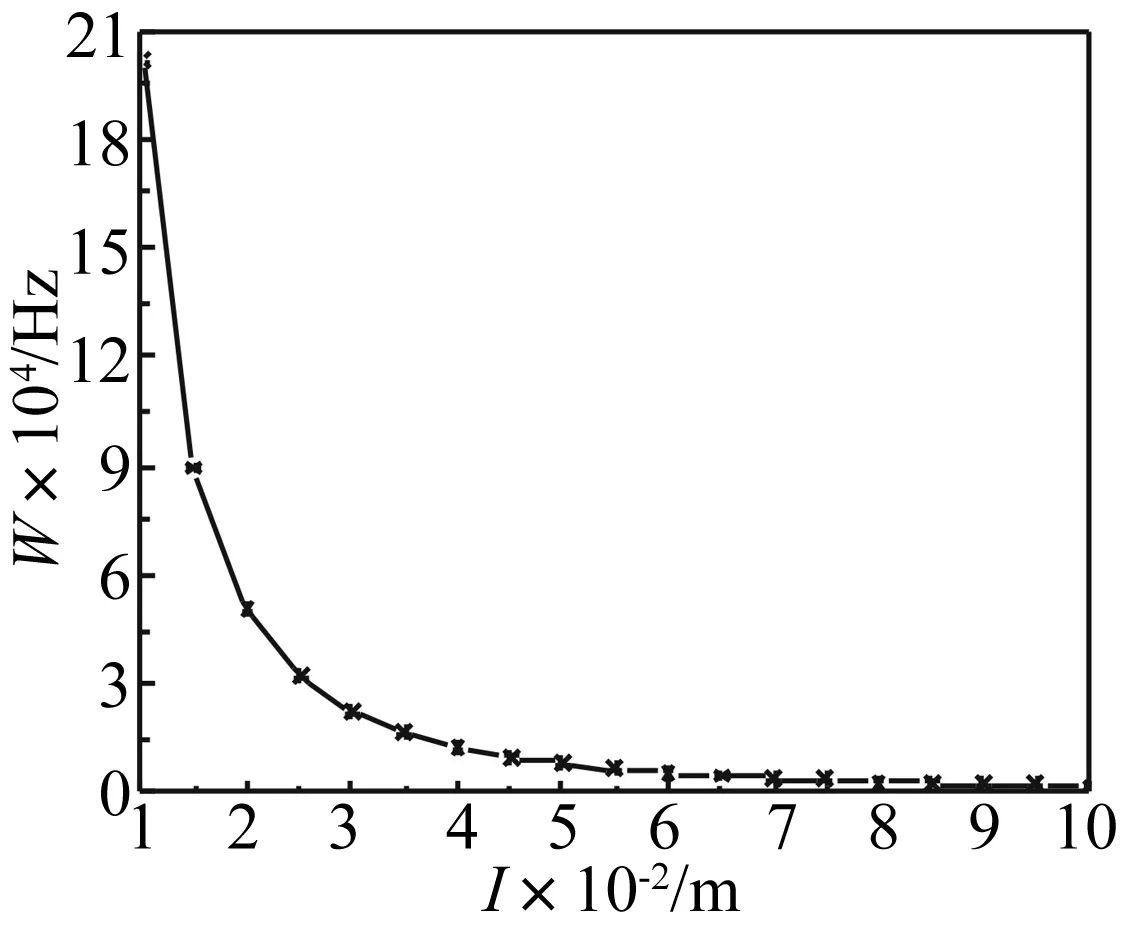
图4 薄板频率随边长变化曲线
5 结 论
本文将PCB板简化为四边固支的矩形薄板,推导了热环境下四边固支矩形薄板的自由振动微分方程,将热载下四边固支薄板振动问题转换为受面内均布张力固支薄板振动问题。通过虚位移原理,得出了计算热载下四边固支PCB薄板自由振动固有频率和挠度值的方法。
利用固有频率计算方法,讨论了热载下温度、薄板的几何尺寸对PCB矩形薄板自由振动固有频率的影响。随薄板温度升高基本频率近似呈线性降低,温度降低频率则近似线性升高。正方形薄板固有频率随薄板的边长增大而下降,在边长到达某一值时,频率变化趋于平缓。本文结果可为电子封装结构中矩形PCB板在热载下的振动分析以及固有频率的计算提供参考。
[1] Xu Z,Carlson K,Kurschner R,et al.An integrated methodology for surface mount PCB configuration[J].Computers & industrial engineering,1998,35(1): 53-56.
[2] 傅岳鹏,谭凯,田民波.电子封装技术的最新进展[J].半导体技术,2009,34(2): 113-118.
FU Yue-peng,TAN Kai,TIAN Min-bo.Recent development of electronic packaging technology [J].Semiconductor Technology,2009,34(2): 113-118.
[3] 刘芳,孟光,王文.球栅阵列无铅焊点随机振动失效研究[J].振动与冲击,2011,30(6): 269-271.
LIU Fang,MENG Guang,WANG Wen.Failure of BGA lead-free solder joints under random vibration loading[J].Journal of Vibration and Shock,2011,30(6): 269-271.
[4] Chai F,Osterman M.BGA solder life prediction under combined power and temperature cycling condition[C].45th Annual International Symposium on Microelectronics,2012: 531-534.
[5] Liu X,Sooklal V K,Verges M A,et al.Experimental study and life prediction on high cycle vibration fatigue in BGA packages [J].Microelectronics Reliability,2006,46(7):1128-1138.
[6] Wong S F,Malatkar P,Pick C,et al.Vibration testing and analysis of ball grid array package solder joints[C].Electronic Components and Technology Conference,57th.2007:373-380.
[7] 朱继元,周德俭.板级电路热振动耦合特性分析与研究[J].电子机械工程,2007,23(6): 4-7.
ZHU Ji-yuan,ZHOU De-jian.Study and analysis of thermal vibration coupling characteristics of board level circuit modules [J].Electro-mechanical engineering,2007,23(6): 4-7.
[8] Barker D,Vodzak J,Dasgupta A,et al.Combined vibrational and thermal solder joint fatigue: A generalized strain versus life approach [J].Journal of Electronic Packaging,1990,112: 129.
[9] Basaran C,Chandaroy R.Thermomechanical analysis of solder joints under thermal and vibrational loading [J].Transactions-American Society of Mechanical Engineers Journal of Electronic Packaging,2002,124(1): 60-66.
[10] 邓定宇.热与振动联合作用下塑料球栅阵列封装中焊点可靠性分析[D].南京: 南京航空航天大学,2011.
[11] 韩强,黄小清,宁建国.高等板壳理论[M].北京: 科学出版社,2002.
[12] 严宗达,王洪礼.热应力[M].北京: 高等教育出版社,1993.
[13] 程选生,杜永峰,李慧.热载下钢筋混凝土矩形简支薄板的自由振动[J].哈尔滨工业大学学报,2009(6): 174-178.
CHENG Xuan-sheng,DU Yong-feng,LI Hui.Vibration of reinforced concrete rectangular plate subjected to thermal loading condition with simply supported boundary conditions [J].Journal of Harbin Institute of Technology,2009 (6): 174-178.
[14] 程选生,杜永峰,李慧.热环境下混凝土矩形薄板在弹性地基上的振动[J].振动与冲击,2007,26(2): 43-47.
CHENG Xuan-sheng,DU Yong-feng,LI Hui.Vibration of concrete rectangular thin plate subjected to thermal environment with simply supported edges on elastic foundation [J].Journal of Vibration Shock,2007,26(2): 43-47.
[15] 张福范.弹性薄板(第二版) [M].北京: 科学出版社,1984.
[16] 曹国雄.弹性矩形薄板振动[M].北京:中国建筑工业出版社,1983.
[17] 李彦辉.PBGA无铅焊球热疲劳可靠性有限元分析[D].南京: 南京航空航天大学,2010.
