滚动轴承-偏置转子系统涡摆耦合动力学特性研究
2014-09-07梁明轩袁惠群蔡颖颖
梁明轩,袁惠群,,蔡颖颖
(1.东北大学 机械工程与自动化学院,沈阳 110819;2.东北大学 理学院,沈阳 110819)
旋转机械的广泛应用使得滚动轴承-转子系统动力学研究和振动分析显得越来越重要,为了满足滚动轴承-转子系统高转速与高精度设计要求,转子偏置位置、圆盘摆振以及轴承游隙变化逐渐成为不可忽视的影响因素。
滚动轴承-转子系统动力学建模过程中最基础的一步在于对轴承非线性分析模型的建立。Yamamoto等[1-2]研究了滚动轴承VC振动,将对称刚性转子简化为受旋转载荷作用的滚动轴承,对轴承径向游隙引起非线性振动进行了研究;Harris[3]完善并发展了滚动轴承的拟动力学分析理论,成为目前绝大多数滚动轴承非线性分析模型的首选;Jedrzejewski等[4]亦在Harris的基础上,着重分析了离心力和陀螺效应对角接触球轴承刚度及变形的影响规律。张耀强等[5]利用滚动轴承-Jeffcott刚性转子模型研究了转子系统的非线性响应;陈果[6-7]重点研究了含多故障的滚动轴承-转子系统动力学特性;邓四二等[8]建立了航空发动机双转子-滚动轴承耦合动力学模型,考虑了低压转子与高压转子之间的中介轴承游隙以及支承轴承参数,运用Newmark有限元法求解了系统响应。然而,这些研究主要侧重于轴承VC振动以及转子非线性响应,忽略了转子偏置和圆盘摆振的影响。在转子系统耦合振动方面,沈松等[9]考虑圆盘摆振的影响,研究了非稳态油膜力支承下的非对称转子系统随转速的分岔规律;李永强等[10]研究了滑动轴承支承下的碰摩转子弯扭摆耦合非线性振动,但未考虑转子偏置引起的系统刚度变化;袁惠群等[11]通过对磁悬浮轴承非线性力的线性化,建立了磁悬浮轴承弹性转子系统动力学非线性电流控制模型。然而这些转子模型中虽然计入了圆盘摆振因素,但没有深入分析不同圆盘偏置位置对系统涡摆耦合振动的影响规律,且大多为滑动轴承支承或者对轴承非线性力做线性化处理,有的则直接采用刚性支承模型。
基于上述原因,本文通过引入转子偏置量和圆盘摆振,推导了滚动轴承-偏置转子系统运动微分方程,基于滚动轴承非线性赫兹接触力模型,对不同偏置量下系统动力学响应进行数值计算与比较,结合非线性理论,详细讨论了转子偏置、圆盘摆振和滚动轴承游隙之间的相互影响规律。该研究可为滚动轴承-偏置转子系统高转速与高精度设计提供参考依据。
1 滚动轴承-偏置转子动力学建模
考虑转子圆盘偏置引起的陀螺效应和滚动轴承非线性力,基于Jeffcott转子建立滚动轴承-偏置转子系统动力学模型如图1所示,忽略轴的质量,轴长为l,直径为d,偏置刚性薄圆盘距左轴承A的距离为a,设a为转子偏置量,圆盘质量、极转动惯量和直径转动惯量分别为md、Jp和Jd,质量偏心距为e,所受重力为W,两端滚动轴承A和B的集中质量分别为mA和mB。

图1 滚动轴承-偏置转子系统动力学模型
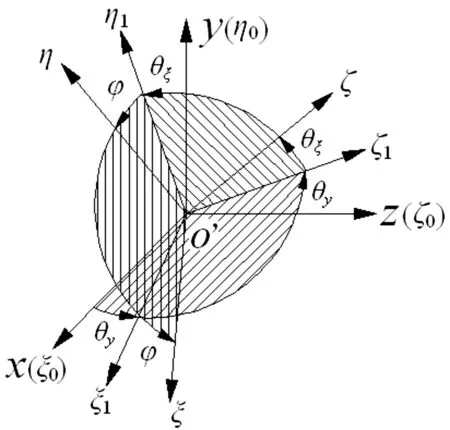
图2 欧拉角示意图
以转子左侧支承的静平衡位置为原点建立坐标系Oxyz,转子轴向方向为Oz轴,垂直方向为Oy轴,水平方向为Ox轴。在转子运动的任意瞬时,两支承中心坐标分别为(xA,yA)和(xB,yB),圆盘形心坐标为O’(x,y),质心为O’e,当转轴变形后,圆盘轴线与支点AB连线的夹角为ψ,圆盘绕x,y轴的偏摆角分别为β和α,设转子的自转角速度为ω,涡动角速度为Ω,则圆盘的陀螺力矩为[12]:
Mg=JpωΩsinψ
(1)
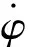
(2)
(3)
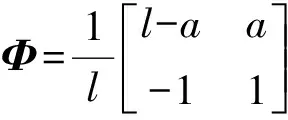
(4)
式中,E为转轴弹性模量,I为转轴截面惯性矩,则Kc=a-1。
设圆盘各方向阻尼互不耦合,大小为c,滚动轴承在x和y方向的阻尼为cb,圆盘与两端支承总耗散能为
(5)

稳态涡动时滚动轴承-偏置转子系统具有8个自由度,由Lagrange方程得转子系统非线性有阻尼涡摆耦合运动微分方程
(6)

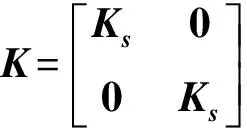
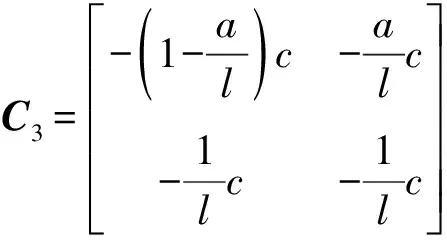
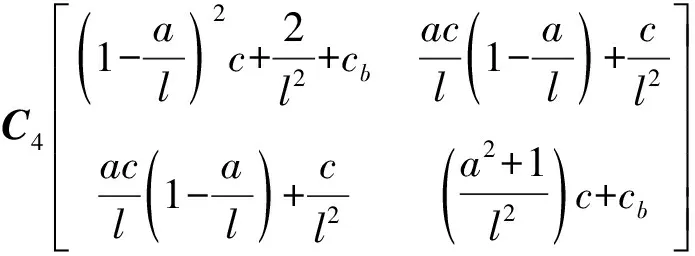
Q为转子不平衡力向量,F为轴承非线性赫兹接触力向量,W为重力场向量。
2 滚动轴承非线性赫兹接触力模型
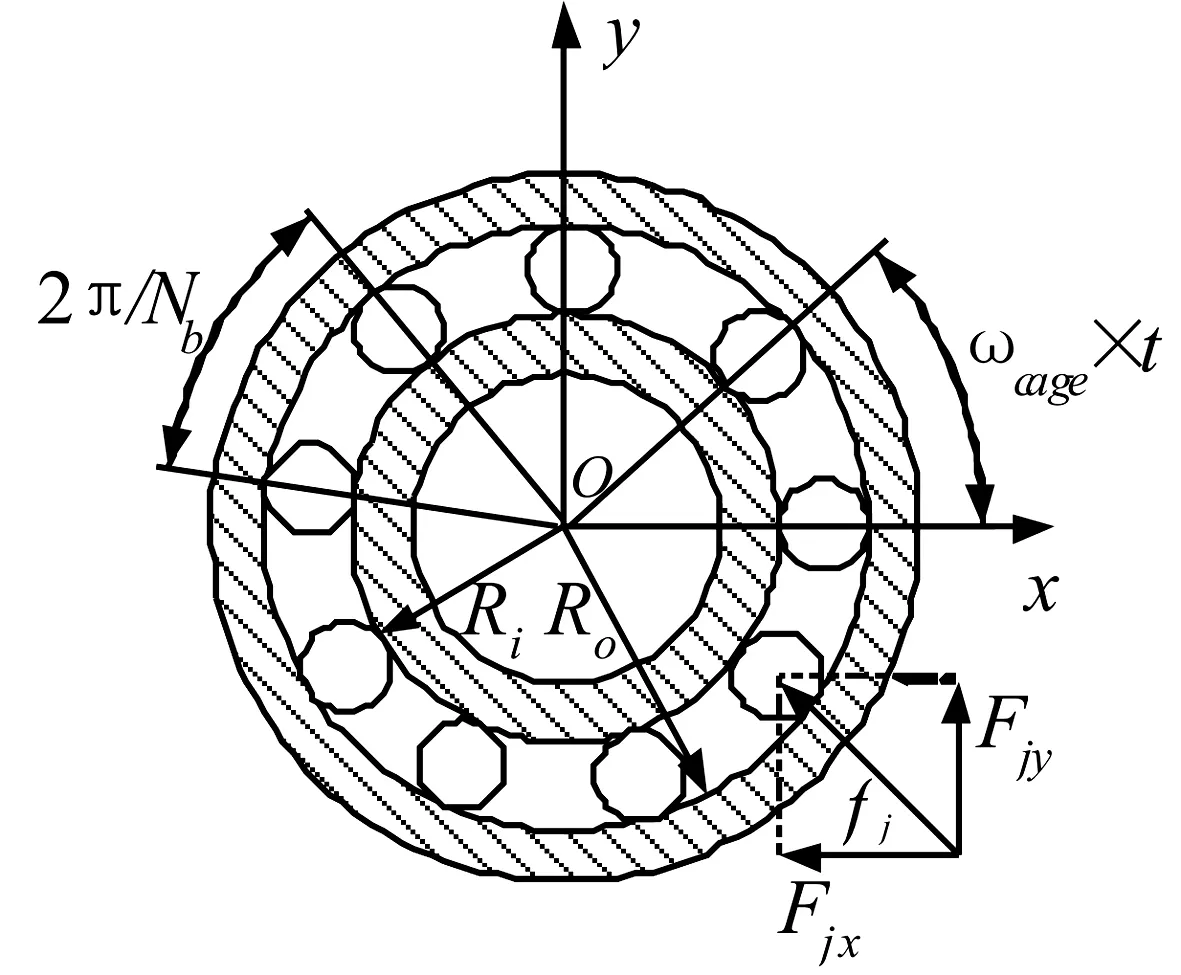
图3 滚动球轴承动力学模型
滚动球轴承动力学模型如图3所示,假设轴承滚动体等距排列且做纯滚动,外圈滚道半径为Ro,内圈滚道半径为Ri,轴承游隙为μ0,滚动体数目为Nb,外圈角速度为ωout,内圈角速度为ωin,保持架角速度为ωcage。由轴承的运动关系得ωout=0,ωin=ω,则
(7)
设φj为任意t时刻第j个滚动体角位置
(8)
式中,j=1,2,3…Nb,φ0为滚动体初始角位置,取φ0=0。滚动体的接触变形量可表示为
δj=xAcosφj+yAsinφj-μ0
(9)
根据滚动轴承非线性赫兹接触理论[3],滚动体与滚道发生接触时产生的非线性接触力为
(10)
式中,kb为滚动体与滚道之间的赫兹接触刚度,λ为滚动体与滚道接触类型相关的系数,点接触λ取3/2,线接触λ取10/9。考虑到接触力的非负性,当δj≤0时,表示无接触力产生,当δj>0时表示有接触力产生。轴承A非线性赫兹接触力表示为
(11)
式中,H(·)表示亥维塞函数
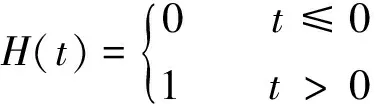
3 滚动轴承-转子系统涡摆耦合振动特性分析
参数选取:md=34.6 kg,mA=mB=2 kg,e=30 μm,Jp=0.7 kg·m2,Jd=0.35 kg·m2,l=0.5 m,d=40 mm,E=2.09×105MPa,c=2 100 N·s/m,cb=1 050 N·s/m。滚动球轴承的参数选取参考了文献[2,7],具体参数如表1所示。

表1 滚动轴承主要参数
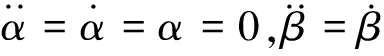
3.1 转子偏置对系统响应的影响
图4为转子偏置量a=l/3,a=l/5和a=l/7时未考虑圆盘摆振和考虑圆盘摆振情况下圆盘x方向位移随转速ω的分岔图。
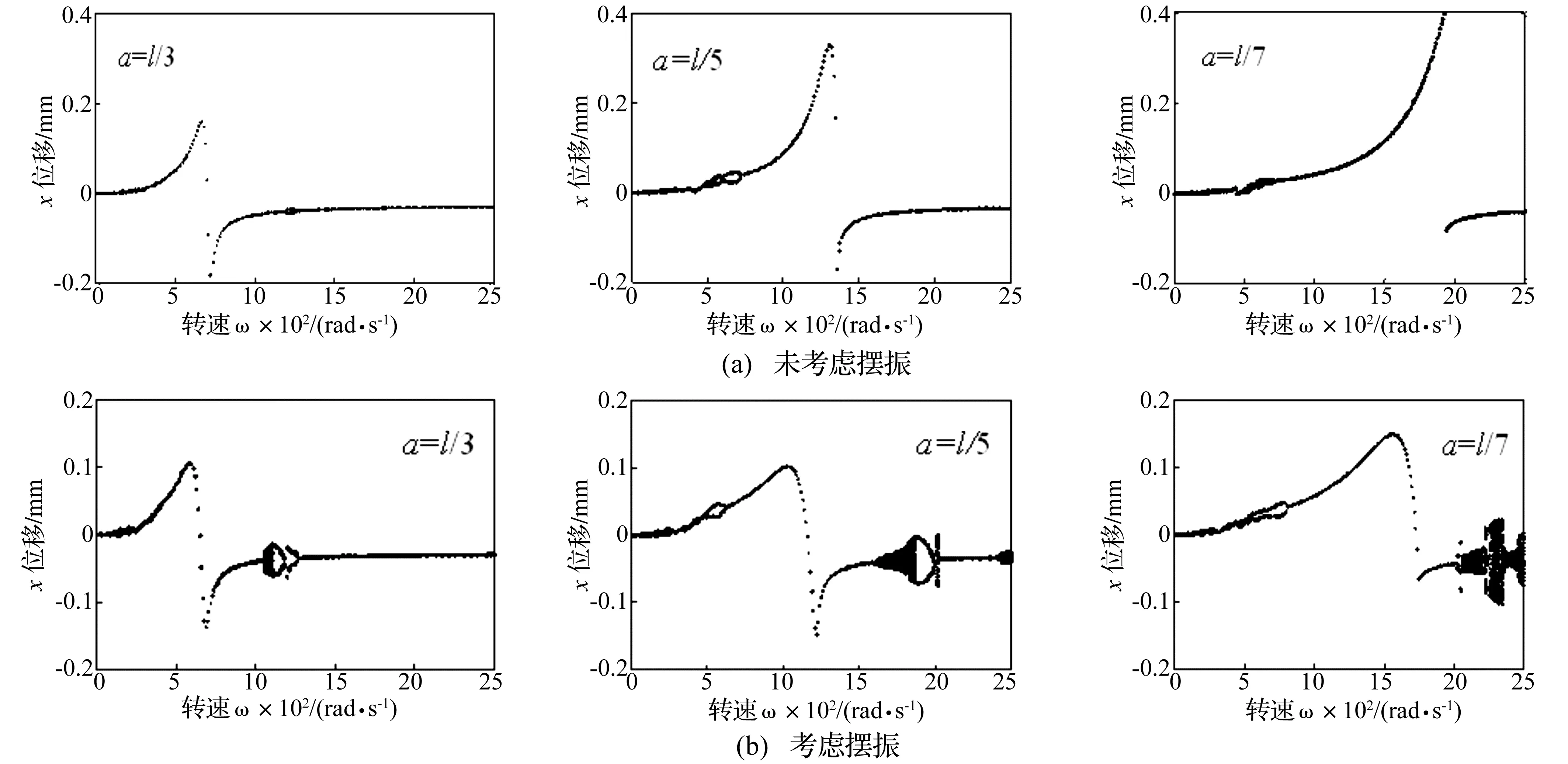
图4 转子系统分岔图
从图4中各响应图可以看出,转子在某一转速附近都有位移响应值突然增大的现象,此时对应着转子系统的临界转速与共振峰值;通过对比发现,考虑圆盘摆振时系统的非线性动力学特征明显增强,且转子偏置程度越大(即a越小),系统高转速下的非线性特征越明显。
表2为a=l/7时未考虑圆盘摆振和考虑圆盘偏摆情况下转子系统响应状态。
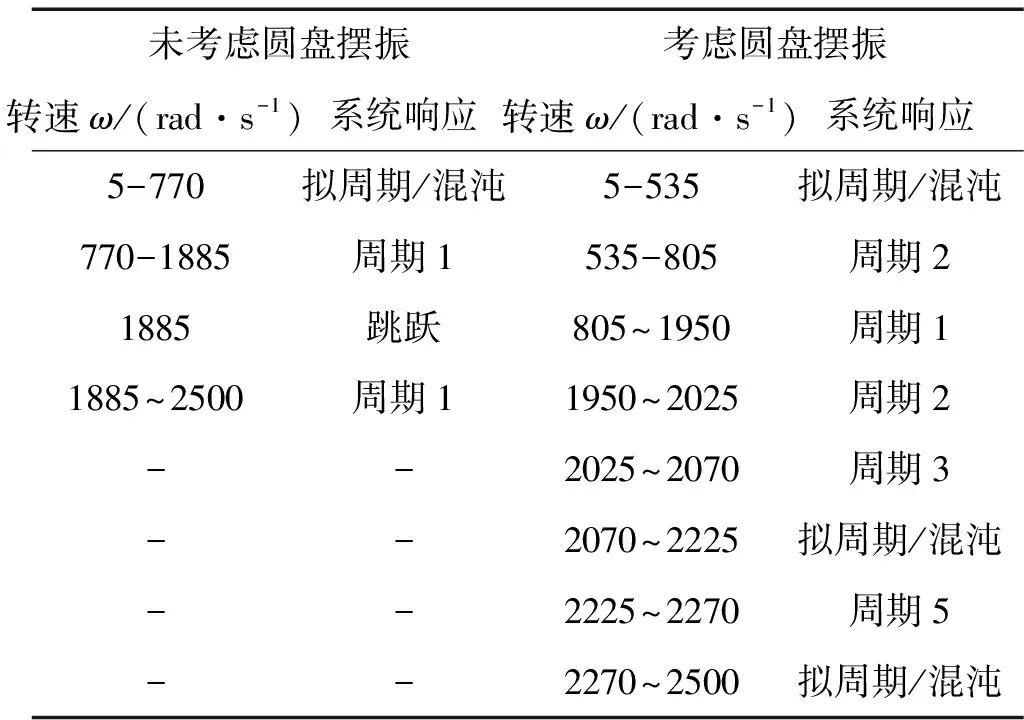
表2 转子系统响应状态
图5为转子偏置量a=l/2和a=l/7时圆盘偏摆角α随转速ω响应图,可以看出转子对称放置(a=l/2)时受支承两端不同非线性轴承力的影响,圆盘亦会产生小幅摆振;圆盘偏摆角随转速的响应规律与圆盘位移的响应规律相似。
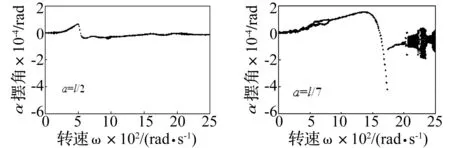
图5 圆盘偏摆角α分岔图
图6(a)、(b)和(c)为偏置量a=l/7情况下,转速ω=780 rad/s,ω=2 200 rad/s和ω=2 255 rad/s的相图与Poincaré图,可以看出三种转速下系统分别处于周期2、拟周期和周期5运动状态。
3.2 转子偏置对系统频率的影响
转子系统中包含两个不同基本频率成分,一个是转子的转动频率,可表示为
(12)
另一个是滚动轴承VC振动频率,这是由于滚动体通过载荷区,轴承径向刚度不相等造成的,可表示为
(13)
式中,BN为滚动轴承VC振动参数,可由轴承结构参数求出,本文中BN=3.47。
图7为偏置量a=l/7,ω=30 rad/s时转子x方向响应图。可以看出由于转速较低,转子不平衡引起的转轴弯曲程度很小,在频谱图中对应的转动频率幅值很小,此时系统频率成分主要表现为轴承VC振动频率及其2倍频。
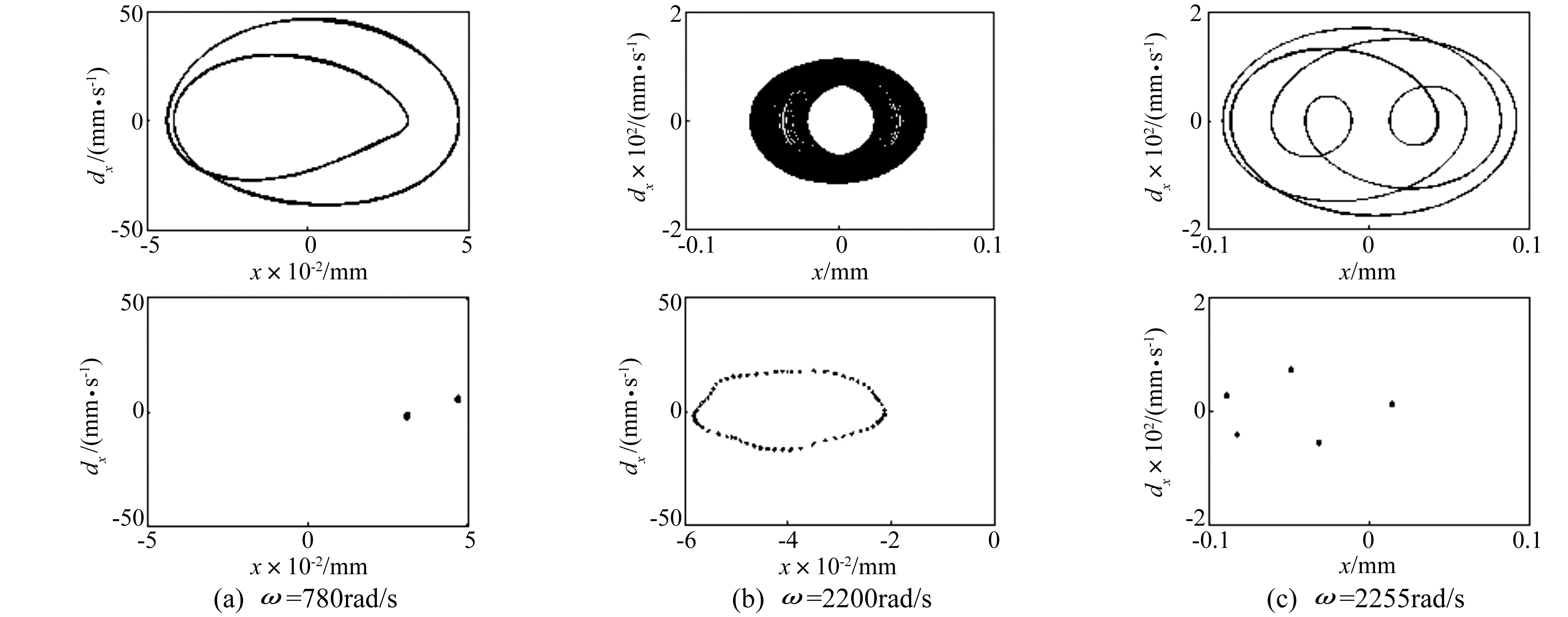
图6 相图和Poincaré图
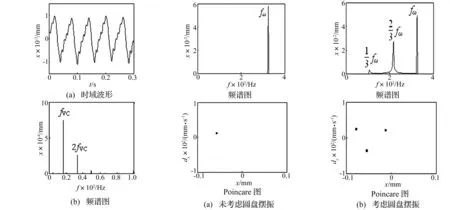
图7 转子响应图
图8(a)和(b)为a=l/7,ω=2 040 rad/s时未考虑圆盘偏摆和考虑偏摆情况下转子响应图,此时转子转速较高,轴承VC振动相对于转轴弯曲振动小很多,系统频率主要为转动频率;但考虑圆盘摆振时系统出现了转动频率的分频成分,可见此时系统的周期3运动主要是由于圆盘偏摆造成的。
为了分析转子偏置程度对系统中各频率成分的影响,选取ω=150 rad/s,该转速不同频率成分在各偏置量的转子系统中均有体现。图9为ω=150 rad/s,偏置量分别为a=l/2,a=l/3,a=l/5,a=l/7和a=l/9情况下转子系统频谱图。
从图9可以看出该转速下不同偏置量的转子系统中同时存在转动频率fω和轴承VC频率fVC以及它们和或者差的组合频率;通过对比可以发现,随着偏置程度的增大,转动频率幅值逐渐减小,VC频率与转动频率的差频率逐渐消失,而两者的和频率逐渐出现;当a=l/9时,系统中又出现了2倍VC频率与转动频率的和频率。
3.3 轴承游隙对系统涡摆耦合振动的影响
取轴承游隙μ0在-10-40 μm内变化,分析轴承游隙对转子系统涡摆耦合振动的影响规律。图10为不同偏置量下转子系统的临界转速ωn随轴承游隙μ0的变化情况。
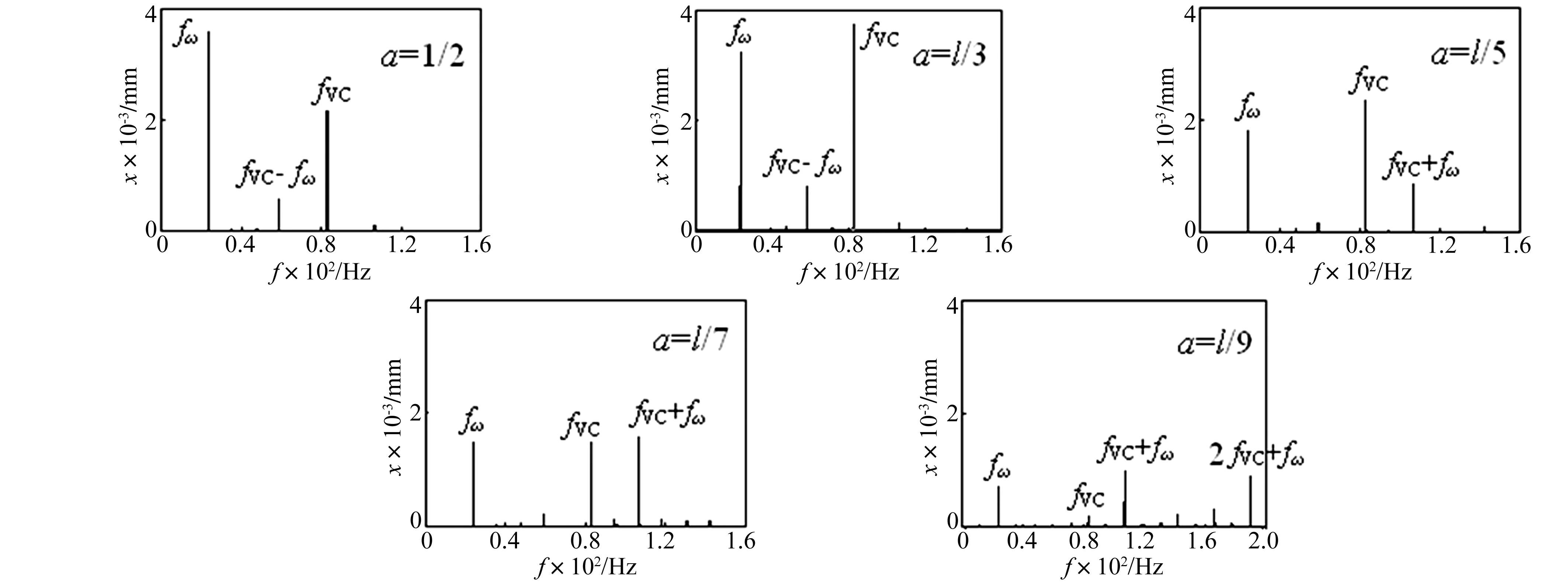
图9 不同偏置量下频谱图

图10 临界转速随轴承游隙变化情况
从图10可以看出,随滚动轴承游隙的增加,转子系统临界转速呈递减趋势,且接近线性递减。通过图10可知不同偏置量下系统临界转速随轴承游隙的递减速率,如表3所示。
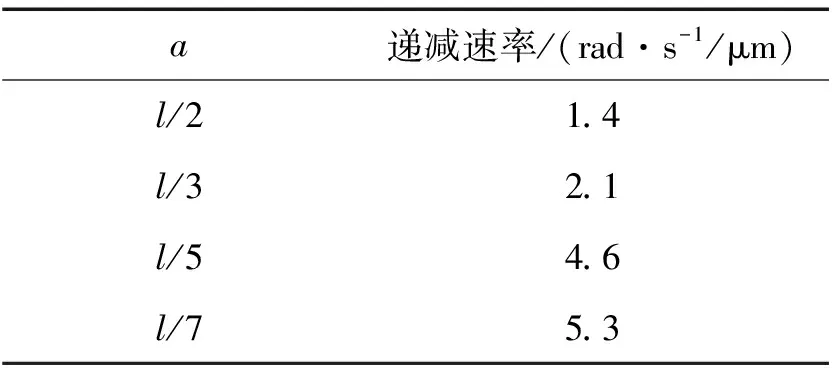
表3 临界转速随轴承游隙递减速率
从表3可知,转子偏置程度越大,系统临界转速随轴承游隙增加而递减速率越大,表明临界转速对轴承游隙变化的敏感度越高,主要是由于增加轴承游隙相当于减小了转子的支承刚度,且圆盘偏置量越大,系统临界转速受支承刚度的影响越大。图11为不同偏置量下系统共振峰值X与圆盘最大偏摆角αmax随滚动轴承游隙μ0变化情况。
从图11可以看出,随滚动轴承游隙的增加,对称转子系统 (a=l/2) 的共振峰值X并非单调变化,而是先增大后减小,圆盘最大偏摆角αmax呈增大趋势;偏置转子系统(a=l/3,a=l/5,a=l/7) 的共振峰值X接近线性递增,圆盘最大偏摆角αmax则先增大后减小。
4 结 论
为了分析转子偏置,圆盘摆振以及轴承游隙等对滚动轴承-偏置转子系统动力学特性的影响,建立了滚动轴承支承下转子系统涡摆耦合运动微分方程,通过对一定参数范围内转子系统动力学特性的对比分析,得出如下主要结论:
(1) 转子偏置引起的圆盘摆振使系统的非线性动力学特性显著增强,且偏置程度越大,圆盘摆振对系统非线性响应的影响越明显。
(2) 一定转速下,不同偏置量下的转子系统中存在不同的频率成分。随着偏置程度的增大,转动频率幅值会相对减小,轴承VC频率与转动频率的差频率逐渐消失,两者的和频率逐渐出现。
(3) 轴承游隙变化对不同偏置量的转子涡摆耦合振动规律的影响不同。转子偏置程度越大,系统临界转速对轴承游隙的敏感度越高;随着轴承游隙的增加,对称转子系统共振峰值呈非单调性变化,而偏置转子系统共振峰值接近线性递增。
[1] Yamamoto T.On the vibration of a shaft supported by bearing having radial clearance [J].Transactions of the Japanese Society of Mechanical Engineering,1955,21(103):182-192.
[2] Sunnersjo C S.Varying compliance vibrations of rolling bearings[J].Journal of Sound and Vibration,1978,58(3):363-373.
[3] Harris T A.Rolling bearing analysis[M].New York: John Wiley & Sons,2000.
[4] Jedrzejewski J,Kwasny W.Modelling of angular contact ball bearings and axial displacements for high-speed spindles[J].CIRP Annals-Manufacturing Technology,2010,59: 377-382.
[5] 张耀强,陈建军,唐六丁等.滚动轴承-JEFFCOTT转子系统非线性动力响应分析[J].振动与冲击,2008,27(5):56-59.
ZHANG Yao-qiang,CHEN Jian-jun,TANG Liu-ding,et al.Analysis of nonlinear dynamic response of a rolling bearing-JEFFCOTT rotor system [J].Journal of Vibration and Shock,2008,27(5): 56-59.
[6] 陈果.具有不平衡-碰摩耦合故障的转子-滚动轴承系统非线性动力学研究[J].振动与冲击,2008,27(4):43-48.
CHEN Guo.Nonlinear dynamic study on a rotor-ball bearing system with unbalance-rubbing coupling faults[J].Journal of Vibration and Shock,2008,27(4):43-48.
[7] 陈果.含碰摩故障的新型转子-滚动轴承-机匣耦合动力学模型[J].振动工程学报,2009,22(5):538-545.
CHEN Guo.A dynamic model for rotor-ball bearing-stator coupling system with rubbing faults[J].Journal of Vibration Engineering,2009,22(5):538-545.
[8] 邓四二,贺凤祥,杨海生,等.航空发动机双转子-滚动轴承耦合系统的动力特性分析[J].航空动力学报,2010,25(10):2386-2395.
DENG Si-er,HE Feng-xiang,YANG Hai-sheng,et al.Analysis on dynamic characteristics of a dual rotor-rolling bearing coupling system for aero-engine[J].Journal of Aerospace Power,2010,25(10):2386-2395.
[9] 沈松,郑兆昌,应怀樵.非稳态油膜力作用下非对称转子分叉特性[J].振动工程学报,2002,15(4):410-414.
SHEN Song,ZHENG Zhao-chang,YING Huai-qiao.Bifurcation characteristics of unsymmetrical rotor systems under unsteady nonlinear oil-film forces [J].Journal of Vibration Engineering,2002,15(4):410-414.
[10] 李永强,刘杰,刘宇,等.碰摩转子弯扭摆耦合振动非线性动力学特性[J].机械工程学报,2007,43(2):44-49.
LI Yong-qiang,LIU Jie,LIU Yu,et al.Nonlinear dynamics characteristics of rubbing rotor with bending-torsional-pendular coupling vibration [J].Chinese Journal of Mechanical Engineering,2007,43(2): 44-49.
[11] 袁惠群,李莹,李东等.磁悬浮轴承弹性转子非线性系统的建模与控制[J].兵工学报,2011,32(2):247-251.
YUAN Hui-qun,LI Ying,LI Dong,et al.The nonlinear model and control of magnetic suspension bearing flexile rotor[J].Journal of China Ordnance,2011,32(2):247-251.
[12] 钟一谔,何衍宗,王正等.转子动力学[M].北京: 清华大学出版社,1984.
