基于变尺度法的进给系统结构参数辨识方法研究
2014-09-07吴子英刘宏昭刘丽兰姚美倩
吴子英,刘宏昭,王 胜,刘丽兰,姚美倩
(西安理工大学 机械与精密仪器工程学院,西安 710048)
进给伺服系统是数控机床的核心组成部分,是一种精密的位置跟踪与定位系统。一般由控制单元、伺服电机、机械传动部件、执行元件和检测反馈环节等组成。其中,机械传动部件是指将电机的旋转运动变为工作台的直线运动的整个机械传动链,包括丝杠螺母副、齿轮装置等中间传动机构。在进行进给系统动力学研究过程中,其结构参数的准确与否对系统动力学建模与动态特性分析均有着重要的影响。因此,准确合理地识别出系统结构参数是实现系统动态分析与控制的一个关键问题。
目前机械结构的参数辨识多依靠系统的输入输出信息,而且往往需要系统输入是斜坡或简谐等规则信号,然而对于大多数工况运行机器而言,尤其是闭环控制下的进给系统,其输入信息的准确获得具有一定难度。
本文针对数控机床进给系统提出了一种简单有效的结构参数辨识方法。该方法将进给系统简化为单自由度系统模型,建立了进给系统临界爬行速度与其结构参数间的非线性函数关系,并结合优化理论,提出了利用临界爬行速度和BFGS变尺度法辨识进给系统结构参数的新思路。该方法不依赖于系统输入信息,仅需要工作台临界爬行速度数据就可以辨识出相关的结构参数,方法简单易于实施。
1 进给系统结构描述
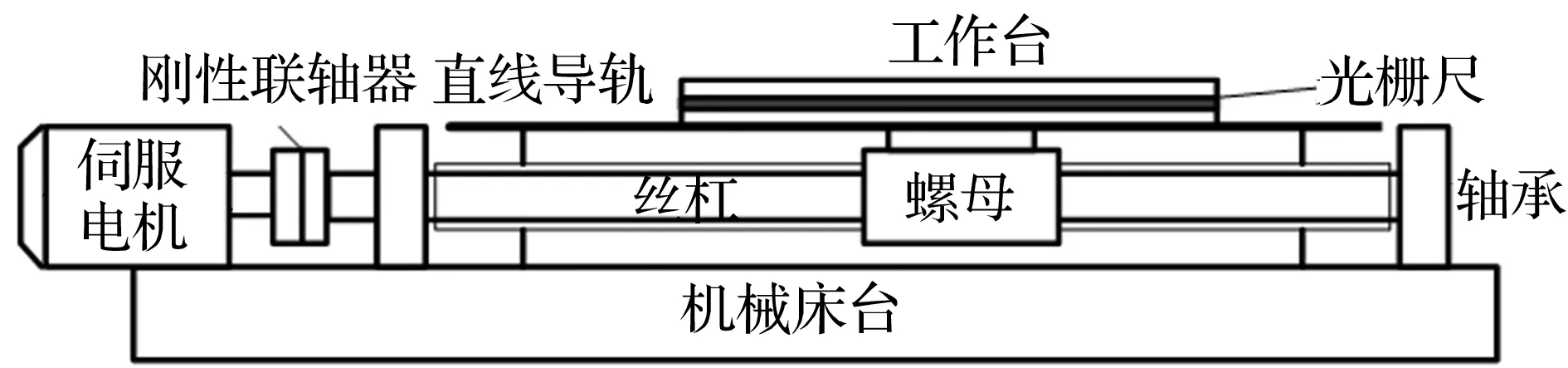
进给系统的一般结构如图1所示,主要由伺服电机、齿轮箱、滚珠丝杠、螺母副、支撑轴承、工作台和导轨等组成。丝杠通过螺母带动工作台,将伺服电机的旋转运动转换成工作台的直线运动。目前,随着伺服电机技术的发展,在负载不大的情况下通常取消了齿轮箱,采用电机和滚珠丝杠直连的方式,缩短了机械传动链,提高了控制精度。而对于重型数控车床来说,该齿轮箱为减速箱,用于提高传动轴的转矩。
2 进给系统力学建模
对于图1所示的进给系统进行建模时作如下两点假设:①螺母的质量相对于工作台的质量忽略不计;②电机轴与轴1之间的联轴器多采用挠性联轴器,在锥套充分锁紧情况下,忽略其变形影响,假设为刚性连接。基于本文目的和所提出的分析方法,需将整个进给系统等效为一个单自由度系统,如图2所示。
在图2中,Me为等效质量,Ke为等效刚度,Ce为等效粘性阻尼,Ff为导轨滑动摩擦力,v为等效质量的驱动速度,x为等效质量的位移。在假设驱动速度为常数的情况下,根据文献[4]可得到质量块Mc发生临界爬行运动时的驱动速度的表达式为
(1)
式中,μs为静摩擦系数,μc为动摩擦系数,ξ为阻尼比。
2.1 等效质量计算
针对图1所示进给系统,根据动能等效原则,将电机转子、中间各轴及轴上齿轮、丝杠轴及丝杠轴上齿轮的转动惯量都向工作台等效,得到系统的等效质量为
(2)
式中,Jm为电机转子转动惯量,J1为轴1转动惯量,J2为轴2转动惯量,Jbs为丝杠轴转动惯量,Jgi为轴上各齿轮转动惯量(i=1,2,3,4),M′为工作台质量,λ为丝杠的导程,r为旋转运动与线性运动的转换系数[7]r=λ/2πm/rad;i1,i2为各级啮合齿轮的传动比。
2.2 等效刚度计算
在图1所示的进给系统中,主要存在传动轴扭转刚度、齿轮啮合刚度、丝杠的扭转刚度和轴向刚度、丝杠螺母副轴向接触刚度及丝杠支承轴承的轴向支承刚度。通常情况下,丝杠支承轴承的轴向刚度都较其他刚度要大得多,可按刚性支承来处理。在图2的等效单自由度力学模型中,为了获得系统等效刚度Ke,首先需要计算出传动链中的各子环节刚度。
(1)轴的扭转刚度
根据材料力学中轴的扭转刚度计算公式,传动轴扭转刚度Kθ及丝杠轴的扭转刚度Kθbs可按下式计算
(3)
(4)
式中,G为剪切弹性模量;d为齿轮轴轴径;dbs为丝杠直径;l为轴长或者丝杠跨距。
(2)丝杠的轴向刚度
对于两端止推支承的丝杠,其轴向刚度为[4]
(5)
式中,a为工作台位置到丝杠左端支承点的距离;E为弹性模量。
(3)齿轮啮合刚度
虽然齿轮在啮合过程中存在双齿啮合区和单齿啮合区,其啮合刚度在运行过程中有时变特征,但为了简化齿轮啮合刚度计算,根据国家标准[5],每一对齿轮的啮合刚度可按下式计算
Ki=(0.75εa+0.25)c′ (i=1,2,…,p)
(6)
且有
(7)

(4)综合扭转刚度
综合扭转刚度Kefθ主要由两部分组成,一部分是由各轴的扭转刚度等效后的扭转刚度Kefθ1,另一部分是由各对啮合齿轮的啮合刚度等效后的扭转刚度Kefθ2。即
(8)
各轴的等效扭转刚度Kefθ1的计算是将各个轴的扭转刚度向丝杠轴等效,即
(9)
式中,Kθi为各轴的扭转刚度(i=1,2)。
同理,各级齿轮啮合刚度的等效扭转刚度Kefθ2为
(10)
式中,mni(i=1,2)为各级啮合斜齿轮的法面模数。
(5)丝杆螺母副轴向接触刚度
根据Hertz理论,可推导出滚珠丝杠螺母副的轴向刚度Knut计算公式[6]
Knut=Nz/δB
(11)
式中,Nz为工作载荷;δB为工作载荷沿轴向位移;
为了简化计算,丝杠螺母副的轴向刚度通常按照定常值处理,其值可由出厂厂家提供。
综上,在上述各刚度计算的基础上,等效刚度Ke由丝杠螺母副的轴向接触刚度、丝杠扭转刚度、丝杠轴向刚度和综合扭转刚度组成,即:
(12)
3 结构参数辨识
3.1 误差函数
将式(2)-式(12)代入式(1)可得到理论上临界爬行速度vc是各齿轮的模数mn、螺旋角β、轴的等效直径di、丝杠直径dbs、丝杠跨度l以及丝杠导程λ等诸多系统结构参数的非线性函数,即
vc=vc(mn,β,di,dbs,l,λ,x)
(13)
通过对进给系统进行测试实验,可以得到工作台不同进给位置下的临界爬行速度的测试数据,即Vcs。这样可以建立理论计算量vc和测试量Vcs的误差函数e,即
(14)
从而根据误差最小原理,利用公式(14),再借助无约束优化方法可将系统结构参数辨识出来。在诸多优化方法中,变尺度法是一种应用较为广泛且易于实现的方法,本文采用了BFGS变尺度法进行最小寻优。
3.2 变尺度法
变尺度法[8]是在克服了梯度法收敛速度慢和牛顿法计算量大的缺点的基础上发展起来的。其基本思想是:利用牛顿法的迭代形式,然而并不直接计算Hessian矩阵[H(x(k))]-1,而是用一个对称正定矩阵A(k)近似的代替[H(x(k))]-1,在迭代过程中,不断改进,最后逼近[H(x(k))]-1。
变尺度法最初的几步迭代与梯度法类似,函数值的下降是最快的,而在最后的几步迭代,变尺度法与牛顿法相近,可较快地收敛到极小点。同时变尺度法避免了计算Hessian矩阵及其逆矩阵,从而克服了牛顿法计算量大的缺点,但保留了较快的收敛速度。因而在目标函数的梯度容易计算的情况下,变尺度法是一种很有效的方法。
BFGS变尺度法迭代公式为
A(k+1)=A(k)+ΔA(k)
(15)
修正矩阵ΔA(k)的形式为
(16)
其中,Δg(k)=f(x(k+1))-f(x(k)),Δx(k)=x(k+1)-x(k)。
BFGS变尺度法具体迭代步骤如下:
步骤1:选定初始点x0,并给定控制精度;
步骤2:置k=0,A(k)=A(0)=I(单位矩阵),从而得到搜索方向为:s(k)=-A(k)f(x(k))=-A(k)g(k);
步骤4:计算g(k+1)=f(x(k+1)),如果,则x(k+1)为极小点,停止迭代,否则转步骤5;
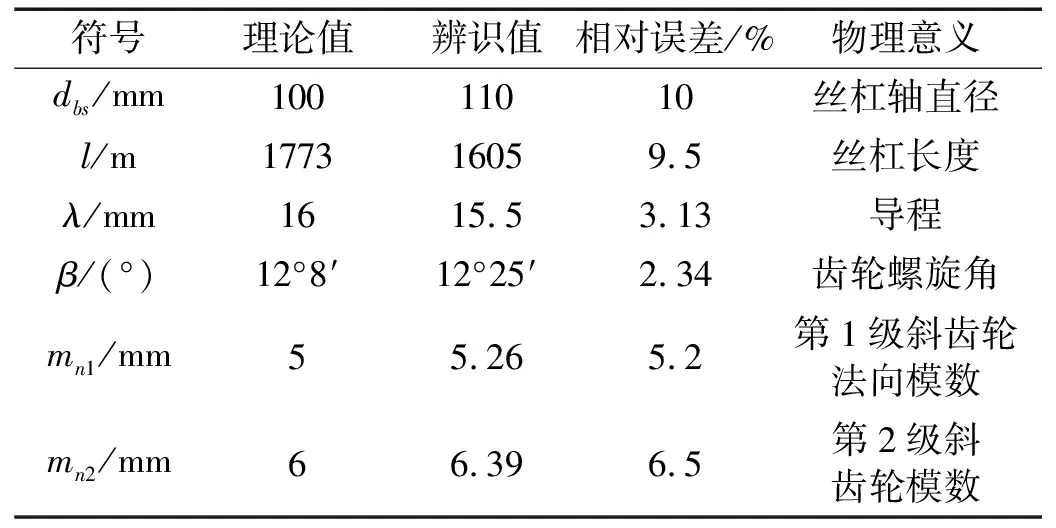
步骤5:检查迭代次数,若k=n,则令x(0)⟸x(k+1),转步骤2,若k 步骤6:计算g(k+1)、Δg(k)=g(k+1)-g(k),Δx(k)=x(k+1)-x(k)及A(k+1)=A(k)+ΔA(k), 步骤7:构造新的搜索方向:s(k+1)=-A(k+1)f(x(k))=-A(k+1)g(k),然后令k⟸k+1,并转向步骤3。 本节以图3所示的直连式进给系统为例进行数值仿真实验,验证所提辨识方法的可行性。该系统无齿轮箱减速环节,工作台两支撑点间的跨距为1 m,理论结构参数由表1给出。 图3 直联式进给系统结构简图 表1 进给系统理论结构参数 基于图2所示的力学建模思想,将该系统简化为单自由度系统,其动力学方程为 (16) 采用四阶龙格库塔法进行数值仿真,得到工作台处在不同位置时的临界爬行速度点,如图4所示。为了增加优化分析的数据量,采用曲线拟合方法对离散的速度点进行拟合,通过比较发现四次多项式拟合的曲线与理论点吻合较好,因此将对四次多项式拟合出的曲线上的数据进行分析。 根据数值仿真实验得到的数据,采用变尺度法辨识出直连式进给系统的结构参数如表2所示。 图4 仿真的临界爬行速度点及其拟合曲线 表2 辨识结果及相对误差 从表2的相对误差值可以看出,变尺度法能够通过优化辨识出系统结构参数且具有较高的辨识精度。仿真中丝杠直径的辨识精度最高,相对而言,丝杠的导程辨识精度略差,相对误差达到3.5%。 以图5所示的某重型数控车床横向进给系统为实验对象,结构简图如图1所示。该系统为全闭环控制,含有二级斜齿轮减速机构,工作台装有光栅尺,可直接测量工作台的直线位移,将信号反馈给伺服电机。 图5 重型数控车床横向进给系统及测量装置 测试装置如图5所示,实验中所使用的仪器有:英国Renishaw XL激光干涉系统测试软件一套;XL-80激光器;三脚架;XC-80环境补偿装置;线性测量镜组;用于将镜组安装到待测平台上的安装组件;笔记本电脑一台。 测试过程中令机床主轴停止转动,横向进给系统空载运行。由于所测试的横向进给系统的行程为1 000 mm,为了测量工作台在不同位置处的临界爬行速度,本次测试共取了8个测点,如图6所示。 利用图5中的实验测量装置,通过反复多次测量取平均值,得到了在各个测点处工作台发生临界爬行运动时的速度值,具体数据列于表3中。并且图7给出了工作台位置与临界爬行速度的关系曲线。 图6 测点布置图 表3 临界爬行速度测量数据 图7 临界爬行速度测点及其拟合曲线 根据图7中的四次拟合曲线的数据,采用变尺度法辨识得到图5中进给系统的丝杠直径、导程及斜齿轮法向模数等结构参数如表4所示。表中理论值为厂家提供。 表4 辨识结果及相对误差 从表4中可以看出,丝杠轴和丝杠长度的辨识精度最低,误差分别达到10%和9.5%。其原因可能在于:①图5所示的结构较为复杂,力学模型建立过程中存在简化,导致辨识精度变低。②由于实验条件限制,该进给系统临界爬行速度点测量较少,经四次曲线拟合后,一定程度上引入数据误差;③多参数优化问题在一定程度上也受到初值的影响,初值的合理选取待进一步研究。 但总体来看,该方法对于其它结构参数的辨识可以给出较为满意的辨识结果,其中斜齿轮的螺旋角辨识精度最高。 本文针对伺服电机驱动滚珠丝杠的进给系统,将其简化为单自由度系统力学模型,借助临界爬行速度计算公式,建立了进给系统临界爬行速度与其结构参数间的非线性函数关系,结合无约束优化理论中的变尺度法,提出了利用临界爬行速度辨识进给系统结构参数辨识的理论及算法。通过对直联式进给系统的数值仿真及某重型数控车床的横向进给系统的工况试验,结果均验证了该方法的可行性和准确性。本文工作为进给系统结构参数辨识及优化的相关研究提供了理论和实验参考。 [1] Brian Armstrong-Hélouvry.Control of Machines with Friction [M].New York: Kluwer,1991. [2] 吴子英,刘宏昭,刘丽兰.考虑摩擦影响的重型车床横向进给伺服系统建模与分析[J].机械工程学报,2012,48(7): 86-93. WU Zi-ying,LIU Hong-zhao,LIU Li-lan.Modeling and analysis of cross feed servo system of heavy duty lathe subjected to friction [J].Journal of Mechanical Engineerin,2012,48(7): 86-93. [3] Naso D,Cupertino F,Turchiano B.NPID and adaptive approximation control of motion systems with friction [J].IEEE Transactions on Control Systems Technology,2012,20(1): 214-222. [4] 戴曙.金属切削机床[M].北京:机械工业出版社,2000. [5] 《中国机械工业标准汇编/齿轮与齿轮传动卷(上)》[M].中国标准出版社,2005,北京. [6] 尹宜勇,祝莉平,贾志新,等.双丝杠与直线导轨结合部静刚度分析[J].农业机械学报,2012,43(6): 202-206. YIN Yi-yong,ZHU Li-ping,JIA Zhi-xin,et al.Static stiffness analysis of joint of double screw and linear guides[J].Transactions of the Chinese Society for Agricultural Machinery,2012,43(6): 202-206. [7] Varanasi K K,Nayfeh S A.The dynamics of lead-screw drives: low-order modeling and experiments[J].Transactions of ASME Journal of Dynamic Systems,Measurement,and control,2004,126(2): 388-395. [8] 丹尼斯(美).等著.无约束最优化与非线性方程的数值方法 [M].北京:科学出版社,2009.4 数值仿真

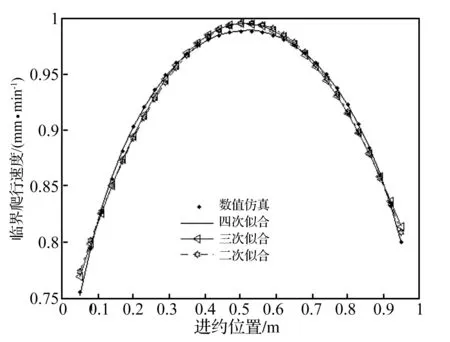

5 实验及结果分析
5.1 测试系统

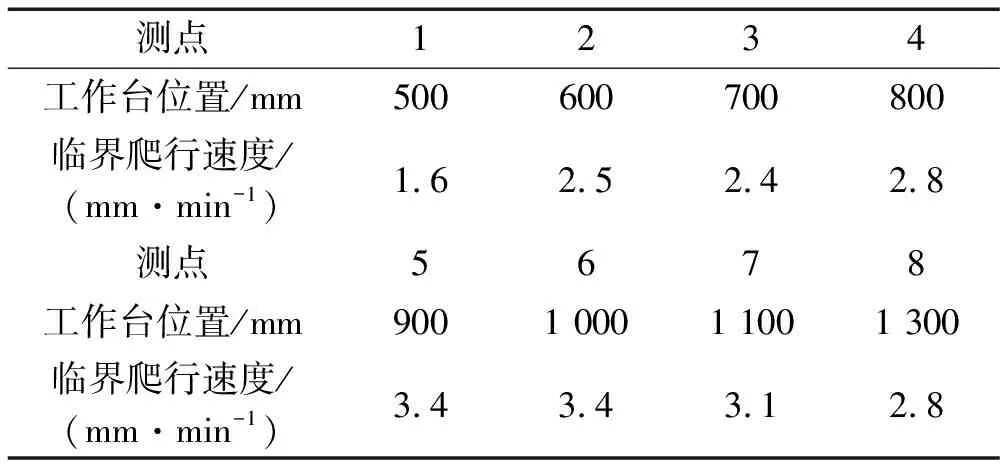
5.2 临界爬行速度测试结果

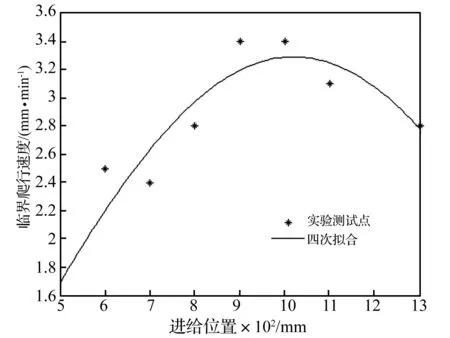
5.3 辨识结果及误差分析
6 结 论
