穿鞋带机械手的动力学分析与仿真

， ，，

(1.浙江纺织服装职业技术学院机电学院，浙江 宁波 315211；2.西安工程大学机电工程学院，陕西 西安 710048)

穿鞋带机械手的动力学分析与仿真

严楠1，2，陈罡1，高晓丁2，孟静2

(1.浙江纺织服装职业技术学院机电学院，浙江 宁波 315211；2.西安工程大学机电工程学院，陕西 西安 710048)

基于ADAMS软件，研究了新型穿鞋带机械手在变负载工作情况下，各驱动关节的力和力矩变化情况，并与空载运行状态进行比较，分析了机械手牵引鞋带翻转过程中对驱动机构的扰动，并对移动副进行了优化设计。分析结果为后续驱动电机选型、零件选择和振动分析提供重要依据，有利于提高机械手的运动控制及动态特性。

ADAMS；关节驱动；穿鞋带机械手；变负载

0 引言

非线性控制研究是工业机械手控制理论研究的重要方面，国内外学者已提出了多种非线性控制系统[1]。在这些非线性控制方法中，变结构控制对参数和负载不敏感，但控制中不可避免地存在抖振；计算力矩控制通过非线性前馈控制，根据给定轨迹实时调节输出力矩，提高了跟随精度[2]，这种控制是最简单、有效的；还有一种分析方法是通过虚功法[3]求解关节力矩，可对于任何自由度数的机械手进行求解，求解结果可用来选择合适的驱动器以及控制机器人的运动。

穿鞋带机械手对运动精度要求比较高，通常需要对结构尺寸、构件重量等方面加以设计与分析。通过测量和控制手部产生的接触力，为提高机械手臂的精度提供了一种有效的方法。此外，当中等刚度的零件相互作用时，相对位置的微小变化会产生较大的接触力。因此，了解并控制这些力可以提高有效位置精度。鞋带的不断伸缩导致张紧力不断变化，这种变负载外力会导致末端执行器发生扰动、振荡等一系列不利问题出现。此外，由于穿鞋带机械手在实际工作中，末端执行器会对机械手各个关节以及驱动装置造成冲击，并产生积累误差，不利于机械手的运动控制。为实现末端执行器牵引鞋带在变负载情况下沿规划路径平稳快速运动，需要实时准确地计算分析这种状态下对所有关节驱动所需的力和力矩，以便在机械手坐标系中提供合适的力和力矩。为提高机械手的精度，减少机械手运动过程中的冲击振动，需要对机械手的4个驱动关节驱动特性进行研究，为后续智能控制研究、电机选型提供参考[4]。

1 穿鞋带机械手组成

穿鞋带机械手是由3个旋转副和1个移动副组成的4自由度工业机械手(“RRPR型”)，其结构如图1所示。4自由度机械手相比6自由度机械手具有如下优点：可以满足大多数工业操作的需要，机构的复杂度和成本低，运动学和动力学模型较简单，控制较容易。穿鞋带机械手的旋转关节分别由各自电机驱动，移动关节由气缸控制。4个驱动关节通过协调控制，实现末端执行器沿着理想轨迹牵引鞋带运动，完成穿鞋带一系列工序。

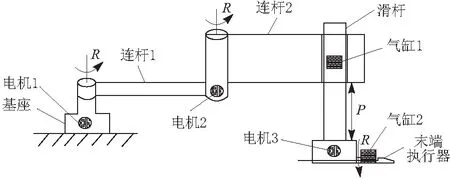
图1 机械手结构

2 机械手动力学数学模型

在此，通过虚功法和Newton-Euler迭代动力学算法来建立关节力学模型。虚功法着重强调力矩模型建立的机理，而Newton-Euler迭代动力学算法主要探究各连杆之间相互作用下的力学特性关系，后者是前者算法的深入求解，通过层进深入，使得机械手的力学数学模型的更完整、准确。

2.1 虚功法求解关节力矩

建立关节力和力矩与机械手坐标系产生的力和力矩之间的关系，根据虚功法[5]可得：

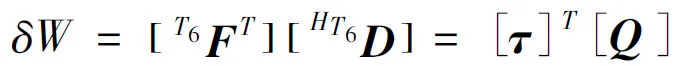
(1)

δW为虚功；F为关节力；D为虚功位移；τ为广义关节列矢量，对于旋转关节为力矩，对于平移关节为力；Q为关节虚拟位移列矢量，对于旋转关节为旋转δq，对于棱柱式关节为平移δd。

定义J为雅可比矩阵，根据雅可比的一般形式可知：

T6D=JQ

(2)

将式(2)代入式(1)可得：

δW=[T6FT]JQ=[τ]T[Q]

(3)

τ=JTT6F

(4)

由以上的运动分析，通过构建机械手的雅可比矩阵J，控制器可根据机械手坐标系中的期望值计算关节力和力矩，并对机械手进行控制。式(4)对于任何自由度数的机械手(欠自由度或冗余自由度系统除外)都是成立的，随着机械手构型的变化，雅可比矩阵也随之发生变化。因此，当机械手运动时，为了在机械手坐标系内持续施加同样的力和力矩，关节处的力矩也要随之变化，需要不断地计算所需的关节力矩。

2.2 Newton-Euler迭代动力学算法

在Newton-Euler迭代动力学算法中，外推内推迭代建立在坐标系之间的力和力矩变换的基础上，依据是单连杆的力平衡和力矩平衡，计算出各连杆运动学和动力学参数关于连杆参数的函数表达式，从而得出机械手的动力学模型。在求解关节力与力矩时进行内推迭代，即从i=4到i=1(从连杆4到连杆1)进行迭代运算，通过下式分别求出各相邻连杆间的相互作用力ifi、作用力矩ini以及各关节力矩τi。

(5)

(6)

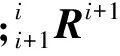
τi=inT(izi)

(7)

zi为关节i的方向矢量。

用笛卡尔空间动力学方程表示出等价的关节力矩为：

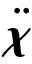
(8)

(9)

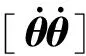
综合上述推导与分析，根据欧拉公式，可以得到封闭式的动力学模型公式为：

(10)

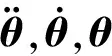
上述方程可用来分析驱动机械手的各个关节所需的动力，也可用来为机械手选择合适的驱动器。动力学数学模型虽然能在理论上展现变负载情况下的机械手关节力与力矩的动力学特性，但缺点是不能连续性地体现机械手动力学状态的变化过程，计算量较大，尤其是在变负载情况下外力输入时刻变化，使得机械手某一特定运动状态的计算更加烦琐，在求逆动力学过程时存在非线性高度耦合计算，又可能导致多解等问题。单纯地构建机械手的动力学数学模型，计算效率低，需要构建试验模型进行仿真以弥补理论计算的不足。

3 系统仿真试验

3.1 构建仿真模型

通过构建穿鞋带机械手的实际动力学模型，基于ADAMS软件，仿真实时反馈变化负载情况下各个驱动关节力和力矩的变化，体现了机械手的外界变负载输入与自身的动力学特性输出过程。

在SolidWorks建立三维模型，以parasolid．x_t格式导入到ADAMS软件，进行相应的重力设置、材料添加(铝)以及约束创建得到分析模型[6]。

穿鞋带机械手在实际工作过程中，机械手姿态以及鞋带张力均处在不同的变化状态，末端执行器受到的是变载荷。机械手末端执行器受到的反作用力fd与工作时间t之间的近似函数关系为：

fd=|sinπt|+2.5

(11)

fd作用方向随鞋带运动而随时变化。

3.2 系统仿真

由式(4)可知，机械手的位姿不同，其构建的自身的速度雅可比矩阵J也发生变化，进而导致机械手的实际运动特性也随之不同。根据建立的动力学模型式(10)可知，可用动力学方程来确定机械装置的运动，只要知道所受到的力和力矩就能确定机械装置运动情况，获取机械手连杆和关节运动的速度、加速度等变化情况，进而对机械手的运动进行仿真。

研究过程为：关节1，2均沿逆时针旋转45°，垂直面内不变，末端执行器牵引鞋带完成上下翻转动作(变向180°)，各关节约束添加如表1所示。设置仿真时间为1.5s，步长100，先后对末端执行器空载和牵引鞋带2种状态分别进行仿真，得到了各关节受到空间力与空间力矩变化情况如图2～图5所示。

表1 各关节驱动函数 (°)/s

驱动关节1关节2关节3关节4运动方式平面旋转平面旋转上下滑动平面旋转大小-30-300120

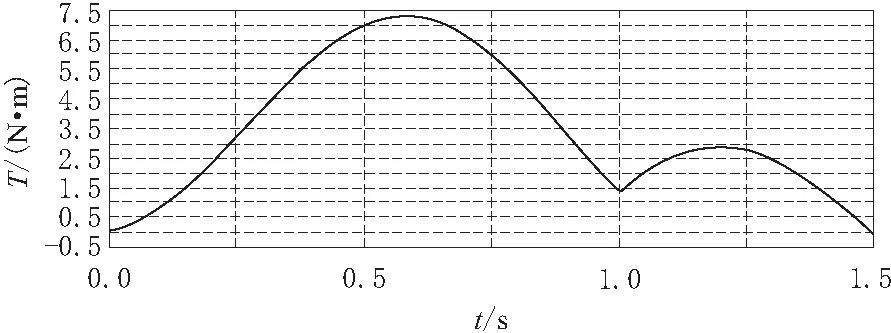
图2 关节1受到的空间力矩(变负载)

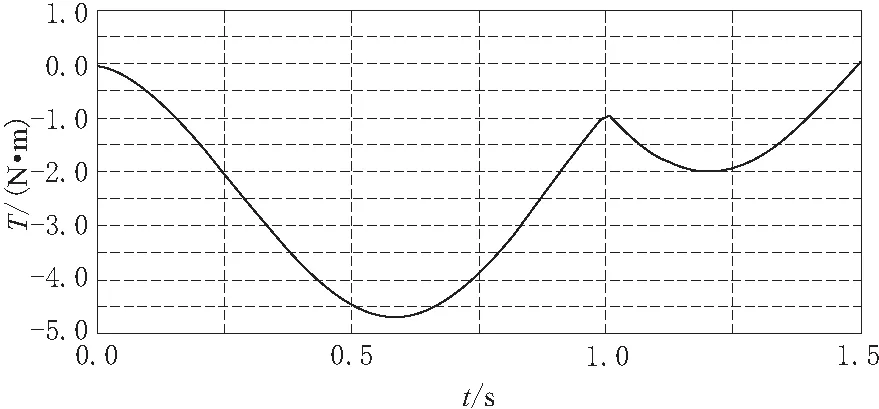
图3 关节2受到的空间力矩(变负载)

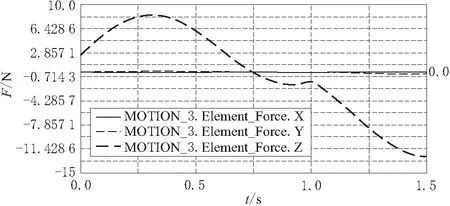
图4 关节3 受到的空间力(变负载)

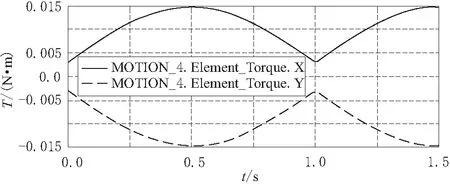
图5 关节4 受到的空间力矩(变负载)

3.3 仿真结果分析

根据仿真结果可知，在0．75s时关节3(移动副)在空间受力为0，这是由于此时刻关节4发生了90°偏转，末端执行器处于垂直状态所致。在1s时，关节1，2的力在竖直面内发生波动，关节4的力矩在水平面内发生波动，这是因为中间采用移动副(关节3)连接所致。在设计时，驱动关节1，2的电机要考虑垂直面的震荡，而关节4的电机要解决实际的力矩输出。旋转副1，2，3在受到外力扰动时，在平面易发生波动干扰，表明垂直面内刚度比水平面好。在机械手运动过程受外力的影响中，关节1处产生最大力矩，并且波动较大；最大空间力发生在关节3运动过程中，需要考虑其竖直方向的振动，同时需要增加其刚性。

3.4 变参数设计研究

“RRPR”型机械手存在一个移动副，直接影响末端执行器在垂直面内的运动，由于该关节的特殊性，应分析样机有关性能对设计变量变化的敏感程度。

在3.2节仿真结果的基础上，只选取移动副关节3的参数性能进行设计研究(其他关节研究类似)。定义末端执行器变负载DV_f为设计变量，将设计变量与滑动副驱动3相关联，定义末端执行器的位移、速度和加速度为测量值，在研究时选取加速度(最小值)为设计目标。根据优化数据分析可知，此状态下移动副加速度大小为0.056 m/s2，为设计变量的最佳取值。

由图6～图8可知，末端执行器在运动过程中位移、速度和加速度光滑平稳过渡，可沿规划轨迹平稳无冲击运动。

图6 末端执行器速度曲线

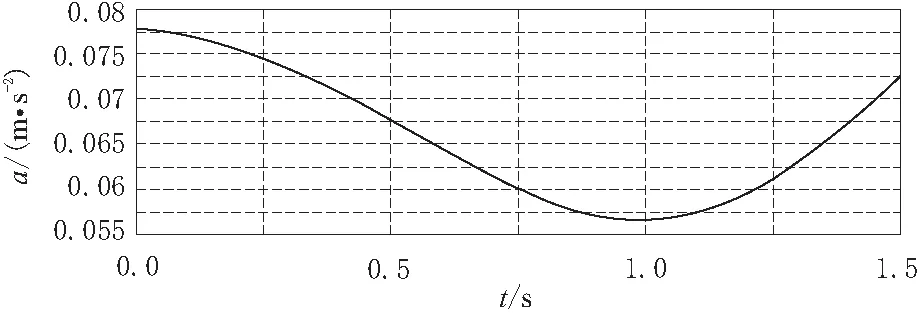
图7 末端执行器加速度曲线

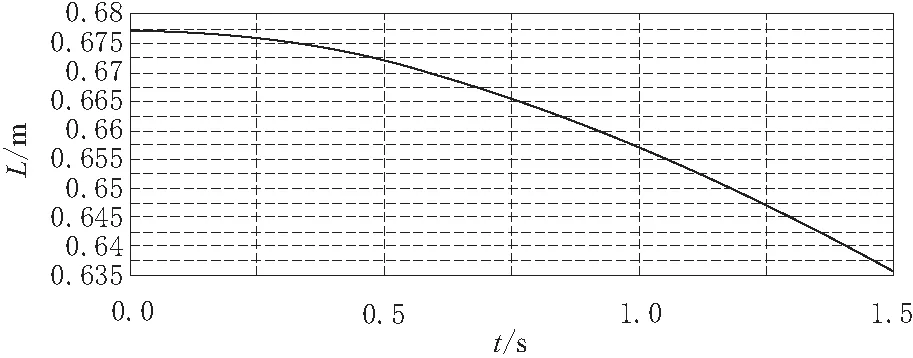
图8 末端执行器位移曲线

4 结束语

根据穿鞋带机械手在实际过程中末端执行器受力的特点，基于ADAMS软件进行动力学仿真，分析了驱动关节的驱动力与力矩的变化情况，对滑动关节的驱动进行了优化。综合以上分析可得以下几点结论:

a.基于ADAMS软件进行系统仿真实验，弥补了动力学理论计算效率低、计算烦琐以及计算过程不连续等缺陷，实现了机械手在运动过程中各关节空间力与力矩动态的连续输出，为后续控制器设计、电机选型、零件选择和力觉控制等提供了重要参考。

b.采用单一变量法，对移动关节进行了变参数优化研究。从移动关节的优化结果看，移动副以0.056 m/s2的加速度运动时，得出的末端执行器加速度、速度曲线平稳光滑，有利于提高机械手的精度和安全性。

c.移动关节3和旋转关节1受外负载变化影响明显，应该增大其刚性。

[1] Zerkaoui S，Badran S M．Stable adaptive neural control of a robot arm[J].Intelligent Control and Automation，2012，3(2)：140-145．

[2] 马 骁，杨志永，王攀峰，等.高速并联机械手动力学建模及计算力矩控制[J].机械设计，2006，23(2)：13-15．

[3] Andrew P，Kiusalaas J．Engineering Mechanics：Statics[M].2nd Edition.Pacific Grove：Brooks/Cole Publishing，1999．

[4] 付 铁，李金泉，杨向东，等．新型码垛机械手的动态载荷计算与选型[J].北京理工大学学报，2008，28(1)：24-26．

[5] 蔡自兴．机器人学[M].北京：清华大学出版社，2009.

[6] 危自强，王家序，肖 科，等．基于 ADAMS 的新型滤波传动件的动力学仿真研究[J].机械传动，2010，34(6)：1-4．

Dynamics Analysis and Simulation of Wearing Shoes Manipulator

YANNan1，2，CHENGang1，GAOXiaoding2，MENGJing2

(1.College of Mechanical and Electrical，Zhejiang Textile and Fashion College，Ningbo 315211，China；2.College of Mechanical and Electrical Engineering，Xi’an Polytechnic University，Xi’an 710048，China)

Change of the force and moment of each driving joint of new wearing shoes manipulator is researched，which is based on ADAMS software under variable load working condition. The disturbance for driving mechanism of manipulator traction shoelaces is analyzed in the process of its flipping，which is compared with the state of no-load running. And optimization design is carried out on the prismatic pair. Important basis is provided for subsequent drive motor selection，selection for material and vibration analysis based on above analysis results，which is also helpful to improve the motion control of manipulator and dynamic characteristics.

ADAMS；joint driving；wearing shoes manipulator；variable load

2014-07-18

产业技术创新及成果产业化重大项目(2013B10013，2013B10045)；浙江省科技厅项目(2013R40025)

TH113；TP241

A

1001-2257(2014)10-0071-04

严楠(1987-)，男，河北唐山人，硕士研究生，研究方向为机械信息测试和控制系统；陈罡(1974-)，男，浙江宁波人，副教授，博士，研究方向为机器人、机电智能控制等。