一对啮合齿轮模型离散成SPH粒子方法研究

·，·

(1.新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046；2.新疆大学机械工程学院, 新疆 乌鲁木齐 830047)

一对啮合齿轮模型离散成SPH粒子方法研究

热合买提江·依明1，买买提明·艾尼2

(1.新疆大学数学与系统科学学院, 新疆 乌鲁木齐 830046；2.新疆大学机械工程学院, 新疆 乌鲁木齐 830047)

利用连续体离散成均匀分布SPH粒子的思路，以渐开线直齿轮为例，通过其各部分曲线进行研究，确定齿轮齿根过渡曲线以及其他部分的参数方程，提出了三维齿轮和一对啮合齿轮模型离散成SPH粒子的方法和算法，编程实现了正确啮合一对齿轮模型离散成SPH粒子的SPH前处理程序。通过用SPH方法对齿轮传动中冲击、接触等问题进行计算和模拟，提供了一种较好的前处理平台。

SPH方法；齿轮过渡曲线；离散粒子；前处理

0 引言

在齿轮传动的研究中，准确绘制齿轮的三维模型是机械设计中的一项重要工作。其中，齿轮的三维模型造型中齿廓线的绘制是难点，主要原因是齿廓曲线较为复杂,尤其是齿根部分的过渡曲线与齿轮的加工方式有关,需要具体分析[1]。

两齿轮高速旋转啮合工作时,由于两齿轮轮齿的相互进入啮合和脱离啮合等因素，将会带来较大的冲击。这种冲击会造成齿轮接触强度或弯曲强度超出许用值，从而导致齿面点蚀或齿根断裂，严重影响机械结构正常运行，甚至会带来较大的事故。为此，对冲击问题的正确评价是至关重要的。冲击问题是一种比较复杂、求解难度大的非线性工程问题。用解析方法和简单的数值方法计算和仿真时，一般都会对问题做大量的简化，不能正确地反映实际情况[2]。基于网格方法分析时，用固定网格很难实时追踪齿轮传动过程。特别是，当面临大变形和裂纹扩散时，出现网格缠结和扭曲，在求解过程中需要实时进行跟踪和网格再划分，这样不仅计算费用昂贵、费时，而且会使计算精度受损[3-5]。近年来，光滑粒子流体动力学(SPH)方法被广泛应用在流体和固体力学领域。SPH方法的基本思想是将齿轮模型离散成有限多个有密度、体积、位置和速度等属性的粒子[6-7]，计算过程中粒子之间不需要网格连接，而通过核函数将它们联系起来，从而保证了物体的连续性，同时满足了能量、动量和质量的守恒性。由于无网格方法可以完全抛开网格并用拉格朗日方法来描述，因此，可直接对物体的实时运动和变形过程进行追踪和坐标更新，而且容易编程实现，从而避免网格奇异性带来的计算误差，保证动态变形和冲击破碎的计算精度。用SPH方法对齿轮传动过程进行数值计算和模拟时，对齿轮传动系统正确和合理离散成SPH粒子模型是非常重要的。

在此，根据连续体离散成均匀分布SPH粒子思路，以渐开线齿轮为例确定齿轮齿廓和轮齿过度曲线参数方程，从而确定齿轮上每一个离散粒子点的原始坐标，根据齿轮啮合原理，通过变换实现一对啮合齿轮离散成SPH粒子，建立了三维SPH离散粒子模型，用RasMol软件来显示所作的模型[8]，并通过所采集齿根、齿廓和齿顶上点的粒子坐标，将它们光滑连接，以检验模型的正确性。

1 连续体离散成SPH粒子的思路

将连续体离散成均匀分布的SPH粒子的基本思路是：当物体的形状为长方形时，相互距离为粒子间距的平面束，先将物体截成若干个矩形截面，然后计算出每个方向能容纳的粒子数，用粒子数、每个方向的长度和粒子间距来确定粒子的坐标(如图 1a 所示)。

当物体的形状为球形、圆柱形和锥形时，相互距离为粒子间距的平面束，先将物体截成若干个圆截面，然后将每个圆截面分解成以一个粒子为中心，半径相差粒子间距的一系列同心圆面，其次计算每个圆的周长和能容纳的粒子数,最后用粒子数、每个圆的周长和粒子间距确定粒子的坐标(如图 1b所示)。

对于齿轮而言，相互距离为粒子间距的平面束，先将齿轮沿着其厚度截成若干个齿轮截面，用齿廓曲线方程计算齿廓线上的点与其中心线上点的相应弧长，来确定每个粒子的坐标(如图 1c所示)，具体实现方法将在下面讨论。

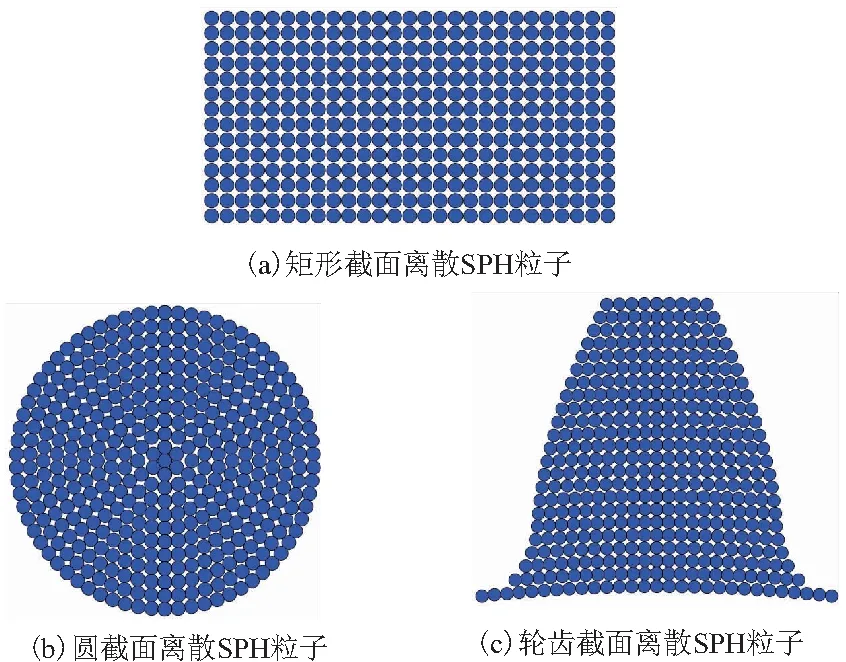
图1 连续体离散SPH粒子

2 齿廓曲线

2.1 齿廓曲线的渐开线方程

由渐开线的形成原理可知，用rb表示基圆半径，rk和θk分别表示渐开线上k点的极径和极角[9]

(1)

αk为k点的压力角。

2.2 齿根过渡曲线方程

用齿条型刀具加工齿轮时，齿条与齿轮的无间隙啮合，刀具的直线部分切除被加工的齿轮齿廓的渐开线部分，过渡曲线部分由刀具的圆角部分切除，加工过程中，刀具的加工节线与齿轮加工节圆发生纯滚动。

刀具齿廓的参数和齿根过渡曲线的参数方程[1]为：

(2)

rp为刀顶圆角半径；a为刀顶圆角圆心Cp距中线的距离；b为刀顶圆角圆心Cp距刀具齿槽中心线的距离；f为齿高系数；c为径向间隙系数。

(3)

2.3 齿轮渐开线与齿根过渡曲线的光滑连接

当极轴与横坐标、极点与原点重合时，由式(1)确定渐开线上的点，旋转θ2才能与由式(3)确定出的齿根过渡曲线，连接为一条完整的光滑齿廓曲线。旋转角度可由式(4)确定，即

(4)

z为齿数。

3 轮齿截面的离散化

离散化轮齿截面时，如图2所示，先对齿根过渡曲线与垂直方向之间的部分进行离散化，再对渐开线与垂直方向之间的部分进行离散化。处理此问题的关键，是要确定对应齿廓曲线上点的半径与垂直方向之间的夹角与弧长。

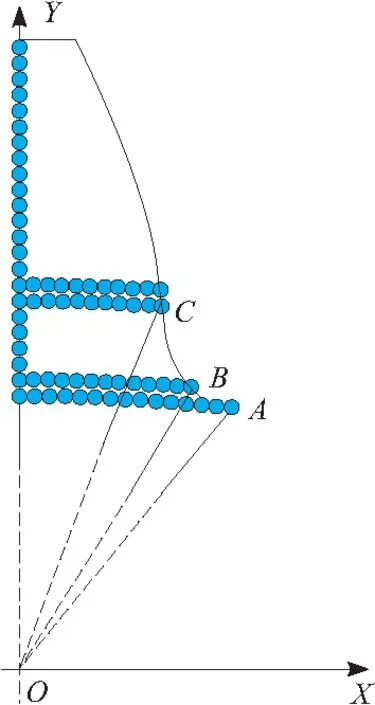
图2 轮齿截面的离散化过程

3.1 齿根过度曲线与轮齿中心线之间的离散化

根据齿根过渡曲线参数方程(3)，可得齿根过渡曲线上对应于α′的半径为：

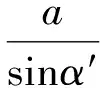
(5)

当α′=π/2时，R(α′)的值最小，记为Rmin;当α′=α时，R(α′)的值最大，记为Rmαx。

假设粒子之间的距离为d，则R(α′)从Rmin每一次增加d到Rmax时，每一个R(α′)对应的α′由式(5)来确定。此时式(5)变成一个非线性方程。本研究用牛顿迭代法求解此非线性方程[10]，确定α′近似数值，计算齿根过渡曲线上的点，然后计算此点与轮齿中心线之间的夹角和弧长。

3.2 渐开线与轮齿中心线之间的离散化

渐开线上的点对应的半径，从齿根过渡曲线最后一个粒子对应的半径Rlast开始，每一次增加d，直到齿顶圆半径Ra。当半径为Rd时，由式(1)可得对应这个半径的压力角αd为：

αd=arccos(rb/Rd)

(6)

由极坐标与直角坐标的关系，对应半径Rd渐开线上点的直角坐标为：

(7)

式(7)确定的点，逆时针旋转θ2后，可计算此点与轮齿中心线之间的夹角和弧长，具体流程如图3所示。

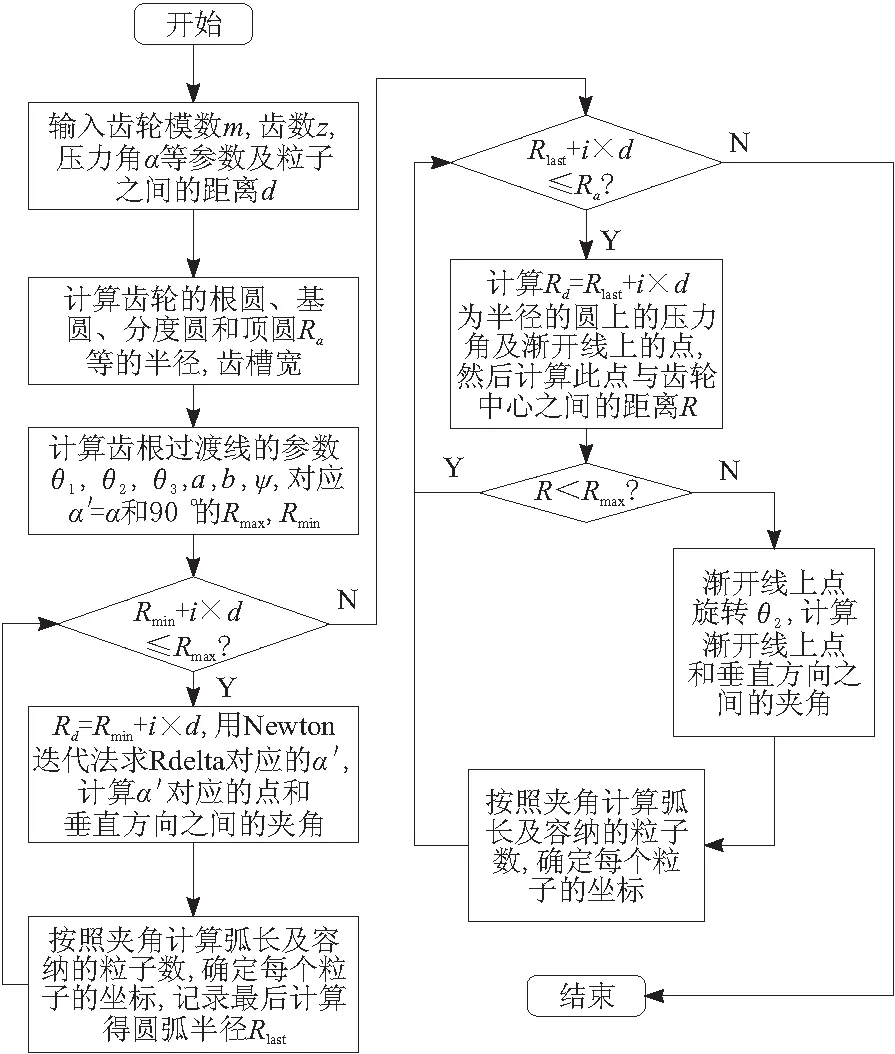
图3 轮齿离散化流程

4 一对啮合齿轮模型SPH离散粒子的建立

用以上所述的离散化思路，确定齿轮上每个SPH离散粒子点的原始坐标。要实现一对啮合齿轮的SPH离散粒子模型，有必要将两轮的每个SPH离散粒子点的坐标通过变换，平移和旋转到啮合位置。主动轮SPH离散粒子点的坐标变换方程为：

(8)

从动轮离散坐标的变换方程为：

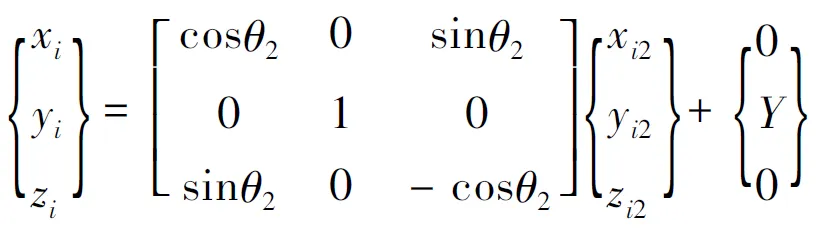
(9)

Y为2个啮合齿轮中心之间的距离；xi1,yi1,zi1为主动轮的SPH离散粒子点的原始坐标；xi2,yi2,zi2为从动轮的SPH离散粒子点的原始坐标；θ1=2π/(4z1)，θ2=2π/(4z2)，z1和z2分别为主动轮和从动轮的齿数。

在以上研究的基础上，编程实现一对啮合齿轮离散SPH粒子程序。在程序中输入齿轮的模数、齿数等参数及粒子间距，将生成RasMol能识别的有每个SPH离散粒子点的坐标信息文件，用RasMol打开此文件，就能看见如图4a所示的模型(模数为10mm，齿数分别为15，30，粒子间距为0.01m)。

将主动轮和从动轮的SPH离散粒子点粒子的坐标采集出来，将它们光滑连接，发现2个齿轮接触在基圆上，如图4b 所示。

图4 啮合齿轮模型

5 结束语

为了用SPH方法对齿轮传动过程进行计算和模拟，建立了一对啮合齿轮的SPH离散粒子模型，确定了齿根过渡曲线、齿廓曲线等的参数方程，编制了实现一对啮合齿轮离散粒子的SPH前处理程序。对模型进行离散的结果显示，此研究可以将一对啮合齿轮正确离散成SPH粒子，并保证离散后正确啮合。为今后用SPH方法分析齿轮传动中冲击、接触等问题，提供了一种较好的前处理平台，具体计算和分析方面的研究将在后续的文章中给出。

[1] 吴继泽,王 统.齿根过渡曲线与齿根应力[M].北京:国防工业出版社, 1989.

[2] 陈 霞,夏巨谌,胡国安,等.直齿圆锥齿轮啮合过程数值模拟[J].机械设计, 2006, 23(4): 21-23.

[3] 贾光辉, 黄 海,胡震东.超高速撞击数值模拟仿真结果分析[J].爆炸与冲击, 2005,25(1): 47-54.

[4] Hwang S C, Lee J H,Lee D H,et al. Contact stress analysis for a pair of mating gears[J].Mathematical and Computer Modeling,2013, 57(1/2):40-49.

[5] 唐进元,刘 欣,戴 进.基于ANSYS/LS-DYNA的齿轮传动线外啮合冲击研究[J].振动与冲击, 2007,26(9):40-44.

[6] Liu M B, Liu G R.Smoothed particle hydrodynamics (SPH):an overview and recent developments[J].Archives of Computational Methods in Engineering, 2010,17(1):25-76.

[7] Kikuchi M, Miyamoto M.Numerical simulation of impact crush/buckling of circular tube using SPH method[J].Key Engineering Materials, 2004, 261/263: 697-702.

[8] Bernstein H J. Manual of RasMol 2.7.5(molecular graphics visualization tool) [EB/OL]. [2014-06-15].http://www.openrasmol.org/doc/.

[9] 孙 恒，陈作模.机械原理[M].北京:高等教育出版社, 1999.

[10] Rahman K, Yimin R, Helil N.A fourth order iterative method for solving nonlinear equations[C]//IEEE International Conference on Computer Science and Information Technology, 2010, 8: 628-630.

Research on a Pair Meshing Gear Model Discrete into SPH Particle

RAHMATJANImin1,MAMTIMINGeni2

(1.College of Mathematics and System Science, Xinjiang University, Urumqi 830046, China；2.School of Mechanical Engineering, Xinjiang University, Urumqi 830047, China)

In this paper,` based on continuums discrete into SPH particles idea ,take involute spur gear as an example, the parameter equations of the transition curve of gear root and the other parts of gear are decided by studied every part curve of gear, provide a algorithm of discrete into SPH particles for 3D gear model and a pair of meshing gear model, programmed pre-processor program for correct meshing a pair of gear, to calculate and simulate impact ad contact in gear transmission to provide a good pre-processor platform.

SPH method;gear transition-curve; discrete particles; pre-processor

2014-06-30

国家自然科学基金资助项目(51075346)

TH112;TH132.4

A

1001-2257(2014)10-0008-04

热合买提江·依明(1974-)，男，新疆伊犁人，讲师，研究方向为机械优化设计与数值模拟研究；买买提明·艾尼(1958-)，男，新疆乌鲁木齐人，教授，博士，博士研究生导师，研究方向为机械设计及理论、计算力学。