Calorific values and ash contents of different parts of Masson pine trees in southern China

Wei-sheng ZENG · Shou-zheng TANG · Qian-hui XIAO

ORIGINAL PAPER

Calorific values and ash contents of different parts of Masson pine trees in southern China

Wei-sheng ZENG · Shou-zheng TANG · Qian-hui XIAO

Received: 2012-12-08; Accepted: 2013-05-25

© Northeast Forestry University and Springer-Verlag Berlin Heidelberg 2014

Calorific value of plants is an important parameter for evaluating and indexing material cycles and energy conversion in forest ecosystems. Based on mensuration data of 150 sample sets, we analyzed the calorific value (CV) and ash content (AC) of different parts of Masson pine (Pinus massoniana) trees in southern China using hypothesis testing and regression analysis. CV and AC of different tree parts were almost significantly different (P＜0.05). In descending order, ash-free calorific value (AFCV) ranked as foliage ＞ branch ＞ stem bark ＞ root ＞ stem wood, and AC ranked as foliage ＞ stem bark ＞ root ＞ branch ＞ stem wood. CV and AC of stem wood from the top, middle and lower sections of trees differed significantly. CV increased from the top to the lower sections of the trunk while AC decreased. Mean gross calorific value (GCV) and AFCV of aboveground parts were significantly higher than those of belowground parts (roots). The mean GCV, AFCV and AC of a whole tree of Masson pine were 21.54 kJ/g, 21.74 kJ/g and 0.90%, respectively. CV and AC of different tree parts were, to some extent, correlated with tree diameter, height and origin.

ash-free calorific value, ash content, gross calorific value, hypothesis testing, regression analysis, Pinus massoniana

Introduction

Calorific value of plants is defined as the amount of heat energy released during combustion of plant tissue. Calorific value (CV) is an important parameter of plants that reflects capacity to fix solar radiation during photosynthesis. CV is also an important index for evaluating material cycles and energy conversion in forest ecosystems. CV is classified into two types: gross calorific value (GCV) or caloric value on oven-dry weight basis, and ash-free calorific value (AFCV) (Bao et al. 2006). Ash is the total amount of mineral content of a plant, which is determined by combusting a given quantity of plant tissue under prescribed conditions and measuring the residue. Ash content can lead to understanding of the material absorption by plants, and reflect the differences of physiological function among various plants or different plants in different regions. Thus, when studying calorific value of plants, GCV and AFCV are usually considered together to estimate the amount of heat energy stored in plants.

Studies abroad on calorific values of plants started in the 1930s. After vigorous development from the 1960s to the 1970s, few studies assessed plant CV (Guan et al. 2005; He et al. 2007). Since the 1980s, the following studies have been reported: Abe (1986) determined CV for 19 coniferous species in Japan, and calculated mean, standard deviation and coefficient of variation as 4972 cal/g, 161 cal/g (1 cal=4.186 J) and 3.2%, respectively. Senelwa and Sims (1999) analyzed the fuel characteristics of biomass from 12 tree species grown under a short rotation forestry regime in New Zealand, where the higher heating value (or gross calorific value) ranged between 19.6−20.5 kJ/g for wood, 17.4−20.6 kJ/g for bark, and 19.5−24.1 kJ/g for leaves. Bhatt and Tomar (2002) analyzed the firewood properties of 26 indigenous mountain tree and shrub species of the northeastern Himalayan region in India, where GCV ranged between 17.90±0.15 −22.94±0.04 kJ/g, AFCV between 18.68±0.31−23.62±0.11 kJ/g, and AC between 1.21%±0.10%−5.43%±0.26%. Kumar et al.(2009) quantified CV, AC, wood density and elemental composition of seven commonly used fuel woods, and reported CV ranged between 19.70−23.40 kJ/g and AC between 1.4%−2.8%. Other reports provided worthwhile references (Wotowicz and Szaniawska 1986; Goel and Behl 1996; Kataki and Konwer 2001; Lemenih and Bekele 2004; Kumar et al. 2010, 2011).

The study of plant CV in China started later and few reports were published before the end of the 1970s (Guan et al. 2005). Since then, plant CV has been reported many times in China (Liu et al. 1990, 1992; Ren et al. 1999; Lin et al. 1999, 2000; Guo 2003; Liao et al. 2004; Fang et al. 2005; Kuang et al. 2005; Chen et al. 2006; Lin et al. 2007; Han et al. 2007). He et al. (2007) compiled reports of GCV of vascular plants in China that covered 129 families, 460 genera, and 1110 species, plus 8 bryophytes studied by the authors themselves. From statistical analysis and hypothesis testing, they presented plant GCV as follows: (1) for different plant parts, mean GCV in descending order was propagule ＞ leaf ＞ branch ＞ bark ＞ stem ＞ root; (2) for different levels of plant communities, GCV ranked as arbor ＞ shrub ＞litter ＞ herbage ＞ bryophyte; (3) for different species groups, GCV ranked as evergreen plants ＞ deciduous plants, coniferous species ＞ broadleaved species. With the development of forestry, bioenergy has attracted research attention in recent years in China. Studies of plant CV have increased in number, and the literature is increasing abundantly (Hao et al. 2008; Wang et al. 2008, 2009; Chen et al. 2008, 2009; Zeng et al. 2009; Kong et al. 2009; Lu et al. 2009; Yang et al. 2010; Zhang et al. 2010a, 2010b; Li et al. 2010; Liu et al. 2010; Jiang et al. 2010; Zhang et al. 2011).

Studies of plant CV were often based on small sample sizes, which hindered representation of average bioenergy levels over large regions. In this study, we used the sample data of 150 trees for Masson pine (Pinus massoniana) in southern China to quantify and compare GCV and AFCV and AC by plant part. We then correlated CV and AC with tree size (diameter, height) and origin. Finally, we compared CV and AC with results reported from related studies, and presented our discussion and conclusions.

Materials and methods

Sample collection

The data used in this study were real measurements of calorific value and ash content which came from the National Biomass Modeling Program in Continuous Forest Inventory (NBMP-CFI) funded by the State Forestry Administration of China. Here only the data of Masson pine (Pinus massoniana) in southern China were utilized, including 150 sample trees obtained from destructive sampling in 2009 (Zeng et al. 2011). The sample trees were located in Jiangsu, Zhejiang, Anhui, Fujian, Jiangxi, Hunan, Guangdong and Guizhou provinces and Guangxi autonomous region (about 20º−35º N, 102º−123º E). Sample trees were selected approximately according to the proportional stocking volume of Masson pine forests in the nine provinces and one autonomous region, and the tree origins were also taken into account. Among the 150 sample trees, 76 were from natural forests and 74 were from plantations. Sample trees were distributed evenly across 10 diameter classes of 2, 4, 6, 8, 12, 16, 20, 26, 32, and ≥38 cm. In addition, the sample trees in each diameter class were distributed by 3−5 height classes as evenly as possible. Thus, the sample trees selected for this study were representative of the large-scale region.

Diameter at breast height and crown diameter of each sample tree were measured in the field. After a sample tree was felled, the total height of the tree (tree height) and the length of live crown were also measured. The fresh mass of stem was summed by three sections (top, middle and bottom), and subsamples of stem wood and stem bark were selected on the trunk at the points of 7/10, 3.5/10 and 1/10 of tree height. The fresh mass of branches was summed by three layers (top, middle and lower), and subsamples of branches without leaves were selected for three layers while a mixed subsample of foliage was selected from all removed leaves of the sample branches. All subsamples were weighed in the field. Among the 150 sample trees, 54 (about 1/3) were selected for measurement of roots. Whole roots of the trees were excavated, and sorted into root stump, large roots (≥10 mm diameter), and small roots (2−10 mm, not including fine roots less than 2 mm). After the total fresh masses of root stump, large and small roots had been weighed, three types of root subsamples were selected and weighed respectively.

Calorific value and ash content determination

Subsamples were oven-dried at 85°C until a constant mass was reached. According to the ratio of dry mass to fresh mass, each component biomass was computed and the aboveground biomass of the tree was obtained by summation. Based on the measurement of dry mass of each subsample, the gross calorific value (GCV) was measured with an oxygen bomb calorimeter at about 20°C. Three repetitions were measured for each subsample, and the arithmetic average was regarded as the mean GCV. The ash content was determined according to dry ashing method. Samples were weighed before they were placed in a furnace at 550°C for 5 hours. Subsequently, the ash was weighed and the ash content was calculated by: ash content = ash mass / total oven-dried mass×100%. Also, the arithmetic average of three repetitions was taken as the ash content (AC). Finally, the ash-free calorific value was calculated as: AFCV = GCV / (1- AC).

Data analysis

Mean GCV, AFCV and AC of stem wood were calculated from the values of three sections (top, middle and bottom) of stem wood through weighting their biomass. Similarly, mean GCV, AFCV and AC of stem were calculated from two values of stem wood and stem bark, and those of aboveground part were calculated from four values of wood, bark, branches and foliage. Consequently, mean GCV, AFCV and AC of belowground part were calculated from three values of root stump, large and small roots through weighting their biomass, and those of a whole tree were calculated from two values of above- and below-groundparts.

The analysis of CV and AC of tree parts included: (1) comparison of mean CV and mean AC of stem wood at three tree heights (top, middle and bottom); (2) comparison of mean CV and mean AC of root stump, large root and small root; (3) ranking and comparing mean CV and mean AC of stem wood, stem bark, branch, foliage and root; (4) correlating mean CV and AC of tree parts with tree diameter, height and origin. Data were analyzed using linear regression.

Hypothesis test

We tested hypotheses by comparing two means. CV and AC for parts of the same tree were not independent of each other, so we used statistical tests for paired data. The t statistic was calculated as follows (Gao 2001):

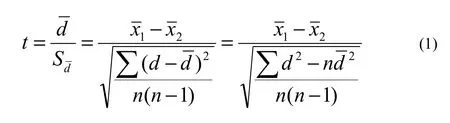
where t is the statistic index, d is the difference of CV or AC from the paired data,d is the mean difference,Sdis the standard error of the difference,x1and x2are the averages of CV or AC of the two data sets, and n is the number of sample trees. The absolute value of t from equation (1) was compared with the critical value of tα(α=0.05) with degrees of freedom df=n-1. When t ＞ tα, the null hypothesis was rejected.

Regression analysis

We used multivariate linear regression analysis (Tang et al. 2008) to correlate CV and AC of plant parts with tree diameter, height and origin. We assumed the calorific value or ash content y and diameter x1, height x2, origin x3(0-planted, 1-natural) were related according to the following linear equation: where ε is the error term, and coefficients a0, a1, a2, and a3can be estimated by the ordinary least squares (OLS) method.

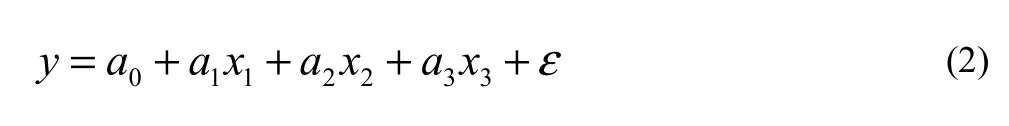
Significance test of the regression: The variation of calorific values or ash contents were classified into two parts, the first was caused by the variation of tree diameter, height and origin which could be explained by equation (2); and the second was caused by other factors and errors. From regression analysis of the data set of observed values for n sample trees, we calculated the F statistic value and significance probability P. When F exceeded the critical value F(fm, fe) where fm and fe were degrees of freedom of the regression and errors, respectively, or P ＜ α, the regression was statistically significant.

Significance test of the coefficients: If the regression model (2) was statistically significant, then the coefficients a1, a2and a3were not all equal to zero. If any one of the coefficients was significantly different from zero, then the corresponding variable was related significantly with CV or AC. We calculated the t statistic and its probability p value for coefficients in the regression.

The fitting results through multivariate linear regression analysis are generally not sound because of the auto-correlation between tree diameter and height. We used principal component regression analysis to avoid the influence on parameter estimation (Gao 2001).

Results

Mean GCV, AC and AFCV for components of 150 Masson pine sample trees are listed in Table 1.

Table 1: Mean calorific values and ash contents for components of Masson pine trees

Calorific values and ash contents of stem woods at different heights

Mean GCVs of stem wood at three tree heights (top, middle and bottom) were 21.09 kJ/g, 21.22 kJ/g, and 21.40 kJ/g, respectively. Mean AFCVs from top to bottom were 21.19 kJ/g, 21.30 kJ/g and 21.44 kJ/g. Mean ACs were 0.47%, 0.40% and 0.21%, respectively. The t statistics for differences between mean values for top, middle and bottom stem wood for GCV, AFCV and AC are listed in Table 2.

Table 2: Calculated t statistics for calorific values and ash contents of stem wood at three heights

It is showed in Table 2 that the GCVs, AFCVs and ACs of stem wood at different heights (top, middle and bottom) were significantly different. CV increased from top to bottom while AC decreased.

Calorific value and ash content of roots by diameter class

GCVs of root stump, large root and small root were 21.30 kJ/g, 21.04 kJ/g and 20.99 kJ/g, respectively. AFCVs were 21.52 kJ/g, 21.46 kJ/g and 21.68 kJ/g, respectively, and AC values were 0.99%, 1.98% and 3.20%, respectively. The t values and their significance for comparison of roots by size class are listed in Table 3.

Mean GCVs, AFCVs and ACs of root stump, large and small roots were significantly different, except for the difference of AFCV between root stump and large root.

Table 3: Calculated t statistics for calorific value and ash content of roots by three size classes

Calorific value and ash content by tree components

Mean GCVs of stem wood, stem bark, branches and foliage were 21.28 kJ/g, 21.40 kJ/g, 22.00 kJ/g and 23.00 kJ/g, respectively. Mean AFCVs were 21.35 kJ/g, 21.71 kJ/g, 22.25 kJ/g and 23.25 kJ/g. Mean ACs were 0.33%, 1.44%, 1.08% and 2.35%, respectively. The t statistics for differences between means for wood, bark, branches and foliage for GCV, AFCV and AC are listed in Table 4.

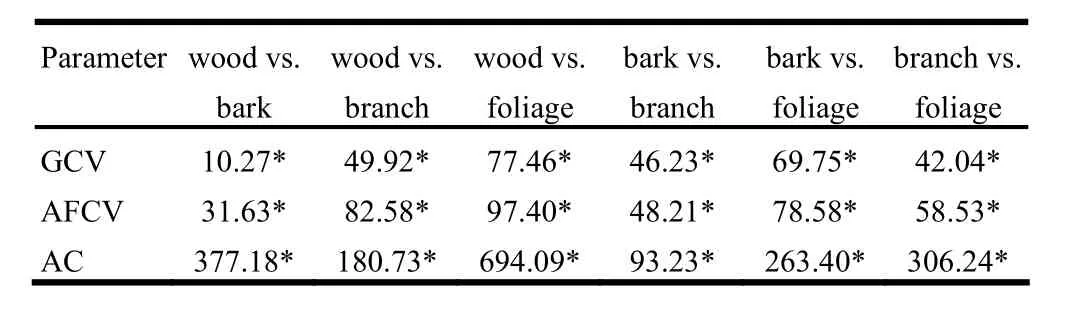
Table 4: Calculated t statistics for mean calorific values and ash contents of aboveground tree components

Correlation analysis of calorific value and ash content of tree components

The F values and P values of regressions (equation 2) and t values and p values of the coefficients for GCVs, AFCVs and ACs of different tree components are listed in Table 5.

All mean GCVs, AFCVs and ACs for different tree components differed significantly. The descending rank orders of mean GCV and mean AFCV were the same, i.e., foliage ＞ branch ＞bark ＞ wood. Mean GCV and mean AFCV of aboveground parts were all higher than means of belowground parts (roots), while mean AC of aboveground parts was lower than that of belowground parts. All differences in means were statistically significant. The comparison between GCVs and AFCVs of whole trees and the different components is shown in Fig.1.

Fig. 1: Comparison between GCVs and AFCVs of different components

Regressions of GCVs and AFCVs on foliage, aboveground part and whole tree and those of ACs on wood, aboveground part and whole tree were statistically significant at the level a=0.05 (Table 5). CVs of aboveground parts and whole tree were positively correlated with tree diameter but negatively correlated with tree height. Also, the ash content of aboveground parts and whole tree were positively correlated with tree diameter and negatively correlated with tree height. By using principal component regression analysis, the F values and determination coefficients R2of regressions (equation 2) and the parameter estimates for GCVs, AFCVs and ACs of aboveground part and whole tree were recalculated (Table 6).

All regressions were statistically significant. From the parameter estimates, it was indicated that calorific values of aboveground part and whole tree were negatively correlated with tree diameter and height. Also, the ash content of whole tree was negatively correlated with tree diameter and height, but that of aboveground part was positively correlated with tree origin. Thismeans the ash content of the aboveground part of a natural tree was higher than that of a planted tree.

Table 5: Hypothesis testing results of regressions for calorific values and ash contents of different tree components

Table 6: The results of principal component regressions for calorific values and ash contents

Discussions

In general, the calorific values of different tree components are ranked as foliage ＞ branch ＞ bark ＞ wood ＞ root (Guan et al. 2005; He et al. 2007). For calorific values of Masson pine, we used more than four studies for comparison. Ren et al. (1999) studied the calorific values of Masson pine in coniferous forest and mixed forest at Dinghushan Biosphere Reserve in Guangdong province, and concluded that the CV of foliage was highest and that of root was lowest. They ranked CVs of different tree components as foliage ＞ branch ＞ wood ＞ root. Guo (2003) analyzed the calorific values of Masson pine in a north suburb of Fuzhou (Fujian province). He reported GCVs and AFCVs ranked as foliage ＞ branch ＞ bark ＞ root ＞ wood. Fang et al. (2005) studied the calorific values of Masson pine at Dinghushan Biosphere Reserve in Guangdong province, and ranked them as bark＞ branch ＞ foliage ＞ wood ＞ root, but the differences between the first three CVs were very small. Zhang et al. (2011) analyzed the calorific values of the main tree species in Guangxi where the GCVs and AFCVs of Masson pine were both ranked as foliage ＞bark＞ branch ＞ wood. The GCVs of Masson pine in this study were ranked as foliage ＞ branch ＞ bark ＞ wood ＞ root, identical to the results of Guan et al. (2005) and He et al. (2007). AFCVs were ranked in this study as foliage ＞ branch ＞ bark ＞ root ＞wood. The little difference between the two ranks resulted fromthe large difference between the ACs of stem wood and root.

Guan et al. (2005) and He et al. (2007) reported that the rank order of calorific values for some plant species might have slight differences. Several studies on calorific value in recent years have proved this prediction. For examples, Zeng et al. (2009) analyzed the calorific values of tree species in five plantation communities on subtropical hilly lands in Heshan county, Guangdong province, and presented that the order of GCVs of different components was foliage ＞ branch ＞ wood ＞ bark ＞ root, and the order of AFCVs was foliage＞ bark＞ branches＞ root＞wood. Zhang et al. (2010) quantified the calorific values of Pinus koraiensis in broad-leaved Korean Pine forests on Changbai Mountain, and reported a rank order of branch ＞ foliage ＞ bark ＞wood ＞ root. Zhang et al. (2010) analyzed the calorific values of five dominant species in broad-leaved Korean Pine forests on Changbai Mountain, where four calorific values of branches were the highest, and three calorific values of foliage were the second. Zhang et al. (2011) reported the calorific values of different components of 12 tree species in Guangxi Zhang Autonomous Region where the rank order of CVs was foliage ＞ branch＞ bark ＞ stem, or foliage ＞ bark ＞ branch ＞ stem.

The calorific values of plants are firstly related to physiological characteristics. Based on the anatomy and physiology of plants, leaves are the most active organs and contain many high-energy compounds such as protein and fat. Leaves can also synthesize high-energy compounds. Thus, the calorific value of foliage is generally highest among plant components. Root, stem and branch are supporting parts in which there are more cellulosic fibers, so the calorific values are relatively low. Furthermore, roots are far from leaves and absorb mineral nutrition and water, thus the calorific value is normally lowest in roots (Guan et al. 2005). Besides the differences in nutritional roles of different plant components, some species have special physiological properties which can result in unusually high or low calorific values. For example, there are high levels of resin and turpentine in pine plants and their calorific values are relatively high (He et al. 2007). The calorific values of plants are not only affected by their composition, structure and function, but also by environmental factors such as illumination intensity, photoperiod, soil type and nutritional condition (Guan et al. 2005).

It is well known that caloric values vary by tree species and components. Bao et al. (2006) discussed the spatial-temporal variation of caloric values among and within plant species and groups, and reported that caloric values of some plants were significantly correlative to age. Qiao et al. (2007) studied caloric value allocation of dominant species in four secondary forests of different ages in Xishuangbanna National Nature Reserve, and concluded that the mean caloric value of dominant species increased with forest age. Kumar et al. (2011) investigated caloric values of three short rotation tree species and found a marginal increase with tree age in all species. The variation of caloric values of Masson pine in this study showed a different pattern, not increasing but decreasing with tree diameter and height, both of which are positively correlative with tree age. In an early study of three Eucalyptus species, Lemenih and Bekele (2004) reported a weak and negative correlation between calorific values and tree age. Additional study is needed to quantify variation patterns of caloric values by tree species and age or size.

The ash content of Masson pine in this study ranked in descending order as foliage ＞ bark ＞ root ＞ branch ＞ wood. This is similar to the results for Masson pine in Guangxi reported by Zhang et al. (2011), but differs from results reported by others. According to Ren et al. (1999), the ash content of root was the highest in Masson pine at Dinghushan in Guangdong province, and that of foliage ranked second. According to Guo (2003), the ash content of root was also highest of plant components of Masson pine in Fuzhou, and the rank order was root ＞ foliage ＞bark ＞ branch ＞ wood. Kataki and Konwer (2001) studied fuelwood characteristics of four indigenous woody species in northeast India and concluded that the ash contents of four species were all ordered as bark ＞ foliage ＞ branches ＞ wood. Zeng et al. (2009) analyzed the ash content of tree species in five plantation communities on the subtropical hilly lands in Heshan county of Guangdong province, and reported a rank of bark ＞ foliage ＞wood ＞ branch ＞ root. Zhang et al. (2010) analyzed the ash content of five dominant species in broad-leaved Korean pine forests on Changbai Mountain, where the ash contents of bark and leaves were highest, those of branches and roots were in the middle, and that of wood was lowest, but the rank orders differed. Liu et al. (2010) compared the ash contents of stem, branch and root of four poplar species, and reported that the ash contents of bark of all three parts were greater than those of wood, then concluded that it might be owing to higher content of mineral elements in bark than in wood. Ash content is the sum of mineral oxidizing materials in a plant and can reflect the function of enriching elements. Ash content varies by plant components and by plant species.

Conclusions

The caloric values and ash contents of tree components of Masson pine in southern China were analyzed in this study based on mensuration data of 150 sample trees. From highest to lowest, GCV ranked as foliage, branch, bark, wood and root; AFCV ranked as foliage, branch, bark, root and wood; and AC ranked as foliage, bark, root, branch and wood. It indicated that crown biomass would be better than stem biomass as fuels for heat energy.

The CV and AC of different plant components were mostly significantly different. Between the top, middle and bottom sections of stem wood, the differences in GCV, AFCV and AC were statistically significant, and CV increased from the top to the lower sections of the trunk while AC decreased. Between the root stump, large and small roots, the differences in GCV, AFCV and AC were significantly different, except for AFCV between root stump and large root, and CV decreased from root stump to large and small roots while AC increased. It meant that larger trunk and root would have better utilization potential of heat energy.

Mean GCV and AFCV of aboveground parts were both higher than those of belowground part (roots) while the mean AC ofaboveground parts was lower than that of belowground parts, and the differences were all statistically significant. It made clear that aboveground biomass would be better than belowground biomass for utilization of heat energy. In addition, the calorific values of aboveground part and whole tree were negatively correlated with tree diameter and height, that is, the smaller the trees, the greater the CV. Also, the ash content of the whole tree was negatively correlated with tree diameter and height.

Acknowledgement

We acknowledge the NBMP-CFI team of the Central South Forest Inventory and Planning Institute of SFA for data collection.

Abe F. 1986. Calorific value of Japanese coniferous wood. Forest Products Chemistry, 36: 91−100.

Bao YJ, Li ZH, Han XG, Song GB, Yang XH, Lü HY. 2006. Plant caloric value and its bio-ecological attributes. Chinese Journal of Ecology, 25(9): 1095−1103 (in Chinese).

Bhatt BP, Tomar JMS. 2002. Firewood properties of some Indian mountain tree and shrub species. Biomass and Bioenergy, 23: 257−260.

Chen B, Yang YC, Zhou Y. 2006. Caloric values of seven dominant species in Tiantong National Forest Park, Zhejiang Province, China. Journal of East China Normal University (Natural Science), (2): 105−111 (in Chinese).

Chen ML, Shangguan ZP. 2008. Characteristics of caloric value and nutrient content of four garden tree species. Chinese Journal of Applied Ecology, 19(4): 747−751 (in Chinese).

Chen ML, Shangguan ZP. 2009. Caloric value and nutrient characteristics of dominant plant species of six typical vegetation communities in Ziwuling Forest Area of the Loess Plateau. Scientia Silvae Sinicae, 45(3): 140−144 (in Chinese).

Fang YT, Mo JM, Li DJ, Cao YS. 2005. Dynamics of energy distribution and its production of a Pinus massoniana community in Dinghushan Biosphere Reserve. Guihaia, 25(1): 26−32 (in Chinese).

Gao HX. 2001. Practical statistical methods and SAS system. Beijing: Peking University Press, 406 pp (in Chinese).

Goel VL, Behl HM. 1996. Fuelwood quality of promising tree species for alkaline soil sites in relation to tree age. Biomass and Bioenergy, 10: 57−61.

Guan LL, Zhou XY, Luo Y. 2005. A review on the study of plant caloric value in China. Chinese Journal of Ecology, 24(4): 452−457 (in Chinese).

Guo JJ. 2003. The biomass and bioenergy of Schima superba and Pinus massoniana forests at north suburb in Fuzhou. China Forestry Science and Technology, 17(supp.): 51−54 (in Chinese).

Han GJ, Cong GL, Shen HL. 2007. Heating value and energy structure of Pinus sylvestris var. mongolica plantation (I): the biomass, heating value, energy pattern and distribution of trees and understory vegetations. Journal of Northeast Forestry University, 35(6): 21−24 (in Chinese).

Hao C, Li HY, Jiang C, Li D, Meng WQ. 2008. Caloric values of dominant plant species on fluvial wetlands of semiarid northern China. Chinese Journal of Ecology, 27(12): 2094−2098 (in Chinese).

He X, Bao WK, Gu B, Zheng WJ, Leng L. 2007. The characteristic of gross caloric values of higher plants in China. Ecology and Environment, 16(3): 973−981 (in Chinese).

Jiang LY, Peng ZD, He BH, Hou ZQ, Du Y. 2010. Caloric value and ash content of Quercus variabilis of six ages. Heilongjiang Agricultural Sciences, (11): 85−89 (in Chinese).

Kataki R, Konwer D. 2001. Fuelwood characteristics of some indigenous woody species of north-east India. Biomass and Bioenergy, 20: 17−23.

Kong WJ, Zhou BZ, Gu XP, An YF, Wen CH, Lu XQ. 2009. Analysis on the caloric values of Bambusa wenchouensis and Dendrocamopsis vario-striata. Scientia Silvae Sinicae, 45(8): 108−112 (in Chinese).

Kuang YW, Wen DZ, Zhou GY, Liu SZ, Zhang DQ. 2005. Caloric values of dominant species in the different layers of lower subtropical monsoon evergreen broadleaved forest at Dinghushan Mountain. Journal of Beijing Forestry University, 27(2): 6−12 (in Chinese).

Kumar JIN, Patel K, Kumar RN, Bhoi RK. 2009. An assessment of Indian fuelwood with regards to properties and environmental impact. Asian Journal on Energy and Environment, 10(2): 99−107.

Kumar R, Pandey KK, Chandrashekar N, Mohan S. 2010. Effect of tree-age on calorific value and other fuel properties of Eucalyptus hybrid. Journal of Forestry Research, 21(4): 514−516.

Kumar R, Pandey KK, Chandrashekar N, Mohan S. 2011. Study of age and height wise variability on calorific value and other fuel properties of Eucalyptus hybrid, Acacia auriculaeformis and Casuarina equisetifolia. Biomass and Bioenergy, 35: 1339−1344.

Lemenih M, Bekele T. 2004. Effect of age on calorific value and some mechanical properties of three Eucalyptus species grown in Ethiopia. Biomass and Bioenergy, 27: 223−232.

Li H, Hu JJ. 2010. Seasonal and annual dynamics of the gross caloric value of eleven poplar and willow clones. Forest Research, 23(3): 425−429 (in Chinese).

Liao CP, Wu CZ, Yan YJ, Huang HT. 2004. Chemical elemental characteristics of biomass fuels in China. Biomass and Bioenergy, 27: 119−130.

Lin H, Cao M, Zhang JH. 2007. Caloric values and energy allocation of a tropical seasonal rain forest and a montane evergreen broadleaved forest in southwest China. Journal of Plant Ecology, 31(6): 1103−1110 (in Chinese).

Lin YM, Lin P, Wang T. 2000. Caloric values and ash contents of some mangrove woods. Chinese Journal of Applied Ecology, 11(2): 181−184 (in Chinese).

Lin YM, Lin P. 1999. Caloric values of two edificators in the typical plant communities in Wuyi Mountains, Fujian. Wuyi Science Journal, 15: 118−123 (in Chinese).

Liu C, Li H. 2010. Comparison of caloric values and ash contents of in the four Populus L. species. Journal of Central South University of Forestry and Technology, 30(10): 24−28 (in Chinese).

Liu SR, Cai TJ, Chai YX, Ding BY. 1990. Energy accumulation, distribution, fixation and transformation in man-made larch forest communities. Journal of Ecology, 9(6): 7−10 (in Chinese).

Liu SR, Wang WZ, Wang MQ. 1992. The characteristics of energy in the formative process of net primary productivity of larch artificial forest ecosystem. Acta Phytoecologica Et Geobotanica Sinica, 16(3): 209−219 (in Chinese).

Lu SB, Rao W, Zhang YJ, Zhu D. 2009. A preliminary study on caloric values and biomass distribution of Phyllostachys edulis cv. Pachyloen. Journal of Bamboo Research, 28(3): 34−37 (in Chinese).

Qiao XJ, Cao M, Lin H. 2007. Caloric values allocation of dominant speciesin four secondary forests at different ages in Xishuangbanna, Southwest China. Journal of Plant Ecology (Chinese Version), 31(2): 326−332 (in Chinese).

Ren H, Peng SL, Liu HX, Cao HL, Huang ZL. 1999. The caloric value of main plant species at Dinghushan, Guangdong, China. Acta Phytoecologica Sinica, 23(2): 148−154 (in Chinese).

Senelwa K, Sims REH. 1999. Fuel characteristics of short rotation forest biomass. Biomass and Bioenergy, 17: 127−140.

Tang SZ, Lang KJ, Li HK. 2008. Statistics and computation of biomathematical models (ForStat course). Beijing: Science Press, 584 pp (in Chinese).

Wang LH, Sun ML. 2008. Caloric values and carbon contents of twelve species of shrubs in northeast China. Journal of Northeast Forestry University, 36(5): 45−46 (in Chinese).

Wang LH, Sun ML. 2009. Caloric values and carbon contents of dominant trees in Xiaoxing’anling forest region. Acta Ecologica Sinica, 29(2): 953−959 (in Chinese).

Wotowicz M, Szaniawska A. 1986. Calorific value, lipid content and radioactivity of common species from Hornsund, Southwest Spitsbergen. Polar Research, 4: 79−84.

Yang GP, Gong HD, Zheng Z, Zhang YP, Liu YH, Lu ZY. 2010. Caloric values and ash content of six dominant tree species in an evergreen broadleaved forest of Ailaoshan, Yunan Province. Journal of Zhejiang Forestry College, 27(2): 251−258 (in Chinese).

Zeng WS, Zhang HR, Tang SZ. 2011. Using the dummy variable model approach to construct compatible single-tree biomass equations at different scales— a case study for Masson pine (Pinus massoniana) in southern China. Canadian Journal of Forest Research, 41: 1547−1554.

Zeng XP, Cai XA, Zhao P, Rao XQ. 2009. Caloric value and ash content of dominant plants in plantation communities in Heshan of Guangdong, China. Chinese Journal of Applied Ecology, 20(3): 485−492 (in Chinese).

Zhang QC, Zhang YN, Qi QG. 2010. Caloric values of Pinus koraiensis in broadleaved Korean pine forests in Changbai Mountain. Scientia Silvae Sinicae, 46(8): 15−21 (in Chinese).

Zhang W, Cai HD, Nong SQ. 2011. The caloric values of main tree species in Guangxi. Central South Forest Inventory and Planning, 30(1): 50−53 (in Chinese).

Zhang YN, Zhang QC, Qi QG, Li JH. 2010. Caloric values and total standing crop of energy of five dominant species in broadleaved Korean pine forest in Changbai Mountains. Journal of Northeast Forestry University, 38(4): 3−5 (in Chinese).

DOI 10.1007/s11676-014-0525-3

Project funding: This work was initiated as part of the National Biomass Modeling Program in Continuous Forest Inventory (NBMP-CFI) funded by the State Forestry Administration of China.

The online version is available at http://www.springerlink.com

Academy of Forest Inventory and Planning，State Forestry Administration, #18 Hepingli East Street, Dongcheng District, Beijing 100714, China. E-mail address: zengweisheng@sohu.com.

Shou-zheng TANG

Research Institute of Forest Resources Information Techniques, Chinese Academy of Forestry, #1 Dongxiaofu, Xiangshan Street, Haidian District, Beijing 100091, China.

Qian-hui XIAO

Central South Forest Inventory and Planning Institute, State Forestry Administration, #143 Xiangzhang East Road, Yuhua District, Changsha, Hunan 410014, China.

Corresponding editor: Hu Yanbo