基于全变分自适应保真项去噪算法的数值实现
2014-09-06王宏志刘婉军
王宏志, 刘婉军, 韩 啸
(1.长春工业大学 计算机科学与工程学院, 长春 130012; 2.吉林大学 学报编辑部, 长春 130012)
基于全变分自适应保真项去噪算法的数值实现
王宏志1, 刘婉军1, 韩 啸2
(1.长春工业大学 计算机科学与工程学院, 长春 130012; 2.吉林大学 学报编辑部, 长春 130012)
基于全变差图像去噪经典算法, 提出一种自适应保真项的数值实现算法.该算法利用图像纹理区和光滑区中噪声的不同特点, 采用不同去噪强度避免传统方法的不足, 并以数值方法实现.在保持经典算法去噪效果的前提下, 解决了原有阶梯效应和过度平滑的问题, 尤其对精致的纹理和细节图像, 使其在去噪的同时, 不丢失图像特点.该方法处理相对简单, 可应用于以偏微分方程为基础的图像处理.
全变分; 梯度抑制; 自适应; 纹理保持
图像在获取、存储和传输过程中常因成像系统硬件设备和传输条件等因素影响而受噪声污染导致图像质量下降.图片的结构信息主要表现为边缘及纹理, 边缘和噪声又同属于高频信息, 因此在处理图像高频信息时, 应做到去噪的同时, 尽量不破坏图像的重要特征.
因为噪声属高频信息, 与图像的主要内容所属频段不同, 从而产生许多滤波方法, 如Gauss滤波、中值滤波和均值滤波等[1], 但这些滤波器的去噪效果也存在不足, 如边缘模糊、不能满足高迭代次数要求[2]等.Rudin等[3]提出了一种全新的全变分(total variation, TV)模型, 这种变分去噪方法基于L1范数, 本质上各向异性扩散, 在去噪的同时可更好地保存边缘信息, 但在平滑区域表现不佳, 会产生阶梯效应[4].目前, 关于全差分去噪主要有基于L2范数、正则项、曲率差分和自适应等算法[5].
为改善图像的阶梯效应, 同时继承全变分算法的保边性, 本文采用自适应保真项在纹理区和光滑区采用不同程度的去噪水平, 以得到更优的去噪效果, 结合图像空间像素点的梯度[6], 参考扩散不动点迭代方法保持算法收敛性, 并给出在笛卡尓网格上的简单数值实现.实验结果表明, 本文算法保存了图像更多的重要特征, 同时得到了更高的峰值信噪比.
1 自适应保真项的全变分模型
1.1经典全变分模型
令I为标准原图,I0为加噪图像, 加性噪声n为0均值、σ2方差, 则有
其中
由于噪声的存在, 使带噪图像的整体梯度比原图I大, 为了消除噪声, 同时又尽量多地保留图片的重要信息, 本文建立目标函数:
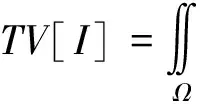
所添加噪声的特性(2)导致了目标函数的最小化约束[7].为了在最小约束情况下求解, 可引入λ(Lagrange乘子)定义一个新能量泛函:
其中: 右边第一项为正则项, 它在最小化过程中可抑制噪声; 右边第二项为逼近保真项, 可保持原图与带噪图片的相似度, 避免图像去噪后出现过大偏差[8];λ为引入的权重系数, 平衡噪声抑制与图像光滑, 是图像去噪的关键.
用最速下降法分析, 在式(4)两边对I求偏导, 得到Euler-Lagrange(E-L)方程为
-
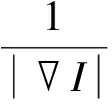
1.2λ的自适应问题
为了得到一个自适应方案, 本文提出一种通过施加空间变化功率约束的方法解决去噪问题.先定义一个局部功率:
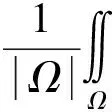
其中:
表示一个径向对称平滑窗, 并满足
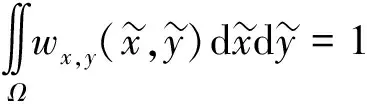
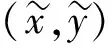
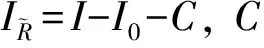
加入Lagrange乘子, 可将最小化问题转换为
对应的E-L方程为
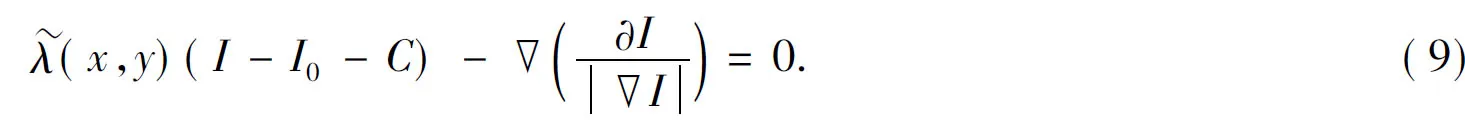
定义
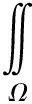
即
Q(x,y)=(I-I0-C)
式(10)成立的充分必要条件为

(11)
此外, 常数C通过∂cE=0可得
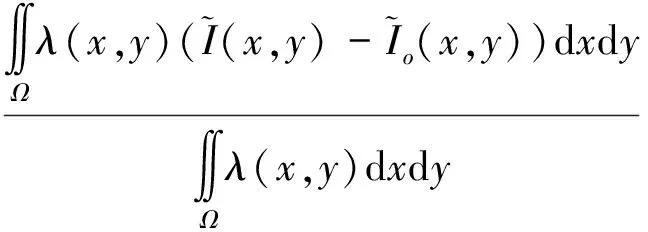
(12)
因此, 式(11)是规整后的保真项参数求解公式, 问题的重点也被缩减为求解S(x,y).
1.3S(x,y)分布的求取
传统图像去噪将图像的纹理区和光滑区一概而论, 得到的去噪结果并不理想[9].尤其对于精致的纹理和细节图像, 当减去大部分噪声后, 图像的大部分特点也被减去.因此, 对于图像的光滑区和纹理区应分开处理[10].图像光滑区域的局部噪声残留较少, 去噪能力可适当减弱,S(x,y)增大使λ值减小,

(13)
本文用图像金字塔模型表示图像Iorig, 对不同区域采用不同的去噪标准[11].卡通图像IC包括大部分轮廓信息, 非卡通图像INC由纹理及小尺度细节组成.于是可将原始清晰图像分为卡通区和非卡通区; 输入图像则包括卡通区、非卡通区和噪声; 大多数自然图像的纹理也包含在残留部分, 所以模型为
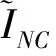

2 模型的数值实现
基于自适应保真项全变分模型, 结合像素梯度, 本文在笛卡尓网格上给出对应的数字实现方法, 并在实验中逐像素实现[12], 如图1所示.其中:A为待处理像素点;N,E,W,S为O的十字区域;Λ0={N,E,W,S};n,e,w,s为4个中间点(不能从图像中直接得到);Λ={n,e,w,s}.

图1 像素点分布Fig.1 Distribution of pixels
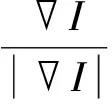
其中h表示像素步长, 通常h=1.然后在中间点上进一步逼近, 以中间点e为例:
同理可用于N,W,S这3个方向上.则
|Ie|=.
(19)
因此, 针对一个像素点的E-L方程可改写为
于是
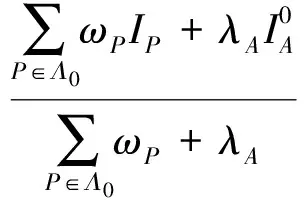
(21)
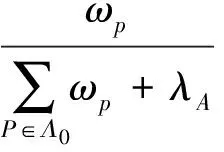
受滞后迭代不动点迭代算法的启发, 结合线性系统迭代格式, 得
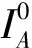
3 实验结果
为验证自适应保真项图像去噪数值计算的效果, 本文分别选取传统TV去噪和自适应保真项去噪与本文算法的实验结果做对比.设步长为0.2, 迭代次数为10次, 当迭代灰度变量小于0.1时终止迭代.实验图片选Lena,Barbara和Toys, 图片大小512×512, 选取101×96图像块进行比较.
输入同一图片, 分别采用全变分(TV)经典算法、自适应保真项TV算法和本文算法对图像进行去噪处理, 结果如图2所示.由图2可见, 传统的TV算法使图像原有的细节信息损失, 且存在块效应; 自适应保真项TV算法的块效应得到改善, 但细节部分信息仍未得到保留; 而本文算法可以保留图像的绝大部分细节特征, 具有更好的视觉效果.
图3为对多种图片的去噪效果比较, 本文算法在去除噪声的同时避免了阶梯效应, 在局部放大图中也看到了更多的细节纹理信息, 如Lena帽子上的羽毛、Barbarad脖子的围巾和小熊衣服格子的细节信息在本文算法下都保存较好.

图2 不同算法在Lena标准图片上的去噪效果Fig.2 Denoising effects of different algorithms on Lena image

图3 不同算法的去噪结果比较Fig.3 Denoising effects of different algorithms
表1列出了不同算法去噪结果的定量值比较.由表1可见, 本文算法可得到约1.1峰值信噪比的增加.

表1 标准测试图像上不同算法的去噪效果定量比较Table 1 Denoising effects via different algorithms on standard test images
综上所述, 本文通过对全变分图像去噪方法的研究, 在自适应保真项的基础上, 建立了自适应保真项TV去噪的数字实现方法.在随机噪声情况下, 能克服原有传统TV方法带来的阶梯效应, 避免边缘过度平滑的同时, 保留了更多图像的细节信息, 使处理的图片得到了更细腻的表现, 并保证在低迭代次数情况下得到更好的峰值信噪比和视觉效果.
[1]Aboshosha A, Hassan M, Ashour M, et al.Image Denoising Based on Spatial Filters, an Analytical Study [C]//The 2009 International Conference on Computer Engineering and Systems.[S.l.]: IEEE, 2009: 245-250.
[2]Russp F.New Method for Performance Evaluation of Grayscale Image Denoising Filters [J].IEEE Signal Processing Letters, 2010, 17(5): 417-420.
[3]Rudin L I, Osher S, Fatemi E.Nonlinear Total Variation Based Noise Removal Algorithms [J].Physica D, 1992, 60(1): 259-268.
[4]Alvarez L, Lions P L, Morel J M.Image Selective Smoothing and Edge Detection by Nonlinear Diffusion [J].SIAM Journal on Numerical Analysis, 1992, 29(3): 845-866.
[5]Blomgren P, Chan T F, Mulet P.Extensions to Total Variation Denoising [C]//Advanced Signal Processing: Algorithms, Architectures, and Implementations Ⅶ.San Diego: SPIE, 1997: 367-375.
[6]Perona P, Mali J.Scale-Space and Edge Detection Using Anisotropic Diffusion [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 1990, 12(7): 629-639.
[7]Chan T F, Esedoglu S.Aspects of Total Variation Regularized L1 Function Approximation [J].SIAM Journal on Applied Mathematics, 2005, 65(5): 1817-1837.
[8]左平, 王洋.一种基于全变差正则化与小波包变换的图像去噪算法 [J].吉林大学学报: 理学版, 2014, 52(1): 81-85.(ZUO Ping, WANG Yang.An Algorithm for Image Denoising Based on Total Variation Regularization Wavelet Packet Transform [J].Journal of Jilin University: Science Edition, 2014, 52(1): 81-85.)
[9]Gonzalez R C, Woods R E, Eddins S L.Digital Image Processing Using MATLAB [M].London: Pearson Higher Isia Education, 2004.
[10]Gilboa G, Zeevi Y Y, Sochen N.Texture Preserving Variational Denoising Using an Adaptive Fidelity Term [C]//Proceedings of Variational and Level Set Methods in Computer Vision.Nice: [s.n.], 2003: 137-144.
[11]Schultz R R, Stevenson R L.A Bayesian Approach to Image Expansion for Improved Definition [J].IEEE Transactions on Image Processing, 1994, 3(3): 233-242.
[12]张强, 王正林.精通MATLAB图像处理 [M].北京: 电子工业出版社, 2009: 199-223.(ZHANG Qiang, WANG Zhenglin.Proficient in MATLAB Image Processing [M].Beijing: Publishing House of Electronics Industry, 2009: 199-223.)
[13]Chan T F, Shen J H.Mathematical Models for Local Non-texture Inpainting [J].SIAM Journal on Applied Mathematics, 2002, 62(3): 1019-1043.
NumericalImplementationofAdaptiveFidelityTermDenoisingAlgorithmBasedonTotalVariation
WANG Hongzhi1, LIU Wanjun1, HAN Xiao2
(1.CollegeofComputerScienceandEngineering,ChangchunUniversityofTechnology,Changchun130012,China;
2.EditorialDepartmentofJournalofJilinUniversity,Changchun130012,China)
On the basis of the classical algorithm of the image denoising based on total variation, a numerical algorithm of total variation based on adaptive fidelity term was proposed.Different intensities of denoising were used to avoid the shortages of the traditional method and then numerical method was chosen so as to realize our algorithm.On the premise of the classical total variation, our method made up for the shortcomings of the original ladder and excessive smoothing effect, especially for the image denoising of fine texture and detail images, it made the remain of most of their image characteristics.Our treatment can be applied to a series of image processing based on partial differential equations simply.
total variation; gradient inhibition; adaptive; texture preserving
2014-03-10.
王宏志(1961—), 男, 汉族, 博士, 教授, 从事数字信号处理及应用、图像处理和通信中信号处理等的研究, E-mail: wanghongzhi@ccut.edu.cn.通信作者: 刘婉军(1989—), 女, 汉族, 硕士研究生, 从事信号与信息处理的研究, E-mail: liuwanjun03220042@126.com; 韩 啸(1981—), 男, 汉族, 博士研究生, 编辑, 从事信号处理与应用及网络协同的研究, E-mail: hanxiao@jlu.edu.cn.
教育部“春晖计划”科研项目(批准号: 403-004077003).
TP181
A
1671-5489(2014)06-1261-06
10.13413/j.cnki.jdxblxb.2014.06.29
韩 啸)
