曲面论基本方程的矩阵推导方法*

邢家省，高建全，罗秀华

(1.北京航空航天大学数学与系统科学学院，数学、信息与行为教育部重点实验室,北京 100191;2.平顶山教育学院，河南 平顶山 467000)

曲面论基本方程的矩阵推导方法*

邢家省1，高建全2，罗秀华2

(1.北京航空航天大学数学与系统科学学院，数学、信息与行为教育部重点实验室,北京 100191;2.平顶山教育学院，河南 平顶山 467000)

从曲面基本方程的矩阵方程表示出发，整体推导曲面的结构方程.此方法以矩阵乘法运算代替繁杂的张量符号变换,不仅使推导过程简化,而且使推导的整体思路更加清晰.

曲面的基本方程;曲面结构方程;矩阵乘法;高斯曲率

曲面论的基本方程和曲面的结构方程是经典微分几何学的重要内容，已构成完善的理论体系，产生了丰富深刻的结果.文献[1-4]采用黎曼张量的记号及求和表示法给出推导转换过程，该推导为后继的黎曼几何学做准备，但这种推导演算繁杂，不利于人们理解掌握.文献[5]中给出了采用曲面方程的矩阵表示及利用矩阵乘法来推导曲面结构方程的方法，此方法简单直接.笔者在综合已有推导转换方法的基础上，利用矩阵乘法给出可推导曲面结构方程的详细过程，实现文献[5-6]中的思想，并对文献[1-8]中的相关结果给出简化的证明方法，由此也能更清楚地看出文献[1-8]中推导方向转换过程的本质.

1 曲面基本方程的矩阵方程表示及其系数矩阵的确定

曲面论的基本问题是研究由曲面的第一、二基本形式如何确定曲面存在的问题，解决的方法是从曲面的基本方程出发，寻找存在可解曲面的充要条件[1-8].

给出C3类的正则曲面Σ:r=r(u1,u2),(u1,u2)∈Δ.按照文献[1-8]中的符号体系，给出如下一系列记号：

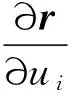
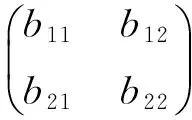
在曲面上选取活动标架[r;r1,r2,n].在曲面上的每一点处，rij表示为r1,r2,n的线性组合，ni表示为r1,r2的线性组合(因为ni与n正交，所以ni与r1,r2共面).令

(1)

(2)

将(1)，(2)式写成矩阵形式，则有

(3)

(4)

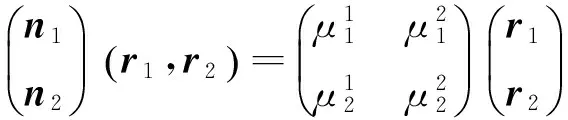
从而

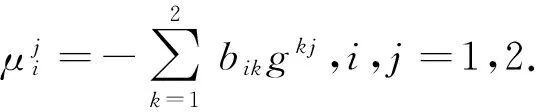
为确定λij,在(1)式的两边与n作内积,即得λij=bij，i,j=1,2；在(3)式两端乘以(r1,r2)，则得

于是，

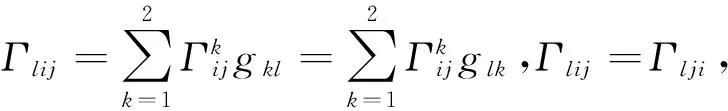
(5)

故有

在(5)式两端取转置，则有

于是，

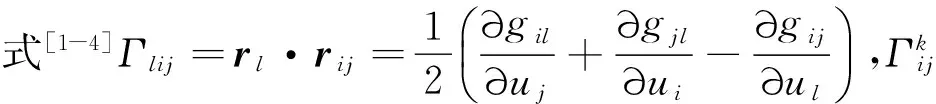
(1)式称为Gauss公式，(2)式称为Weingarten公式.至此得到曲面论的Gauss公式和Weingarten公式(也称为曲面的运动方程，或称为曲面的基本方程).

因为

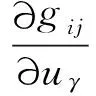
所以

(6)

2 曲面论的基本方程的矩阵方程表示形式

将曲面的基本公式改写成矩阵方程的形式为：

(7)

(8)

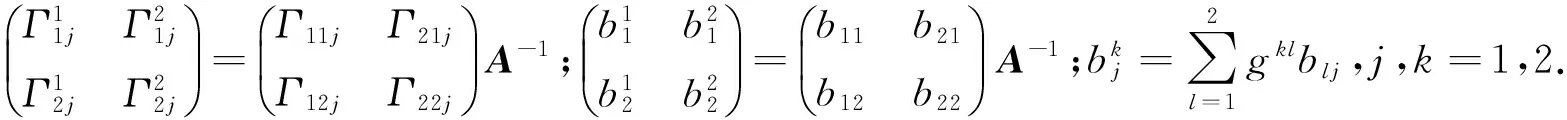
3 曲面基本方程中系数矩阵之间关系的矩阵推导方法

现利用曲面基本方程的矩阵方程表示来研究曲面第一、二基本形式系数之间的关系.

利用(7)式，存在可解曲面的充要条件是

(9)

比较左右两端的系数，可得

(10)

(11)

从而

(12)

(13)

于是(13)式成立.

由此可知(11)式与(12)式是等价的.

4 曲面论基本方程的Gauss方程的矩阵推导方法

现考察(10)式成立的充要条件.

(14)

(15)

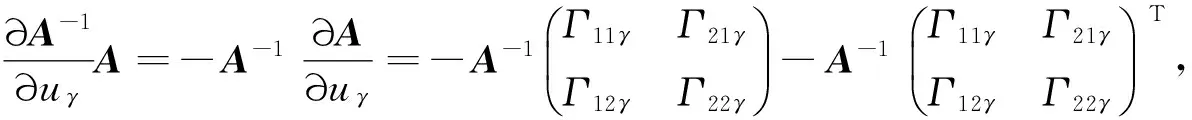
(16)

由(10)，(14)—(16)式，得

(17)

5 曲面的高斯曲率的内蕴计算公式

将(14)式代入(10)式，得

(18)

由(18)式两边矩阵中右上角的元素对应元素相等，得

于是高斯曲率有如下的内蕴计算公式[1-4，6-11]：

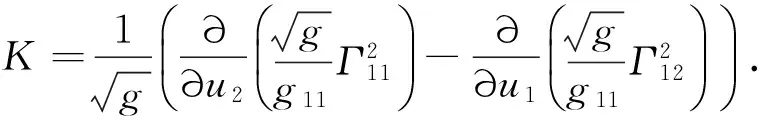
(19)

类似地，

(20)

将(19)和(20)式相加，得到

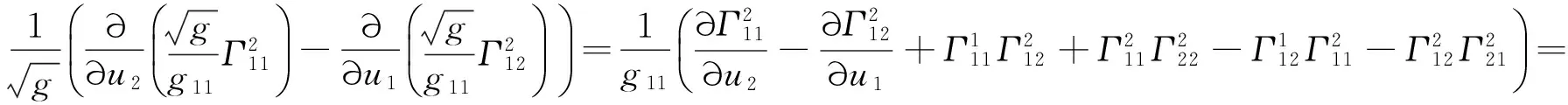
结果得证.

同理，由(18)式两边矩阵中左下角的元素对应元素相等，得

于是高斯曲率有如下的内蕴计算公式[1-4,6-11]：

利用(17)式可得

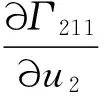
((Γ121g11+Γ221g21)Γ112+(Γ121g12+Γ221g22)Γ212)=

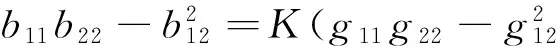
(21)

这里得到的(21)式与高斯曲率是内蕴量的Brioschi公式[1-2,4,7]完全一致.

在正交曲线坐标网下，可以求出系数矩阵，然后代入(21)式，就可给出高斯曲率的计算公式[1-4].利用曲面论的基本方程(1)式，可给出曲面上曲线的测地曲率[1-4,12]和测地挠率[2,4,12]的计算公式的推导.利用曲面论基本方程的矩阵方程表示(7)，(8)式，可以非常方便地给出求解曲面方程的矩阵方程方法[13].

[1] 梅向明,黄敬之.微分几何[M].第4版.北京:高等教育出版社,2008:87-105.

[2] 陈维桓.微分几何[M].北京:北京大学出版社,2006：193-228.

[3] 彭家贵，陈 卿.微分几何[M].北京：高等教育出版社，2002：74-85.

[4] 苏步青，华宣积，忻元龙.实用微分几何引论[M].北京：科学出版社，1986：86-91.

[5] 谢 琳,安 扬.一个利用矩阵整体推导曲面结构方程的方法[J].辽宁师范大学学报：自然科学版，2007,30(3)：262-264.[6] 华罗庚，著.高等数学引论(第2册)[M].王 元，校.北京:科学出版社,2009：315-322.

[7] 陈维桓.微分几何例题详解和习题汇编[M].北京:高等教育出版社,2010：171-219.

[8] 徐冠文.“曲面论的基本定理”教学注记[J].徐州师范学院学报：自然科学版，1989，7(2)：80-86.

[9] 曾宪祖.高斯曲率的一个计算公式的证明[J].云南师范大学学报，1991,11(4):52-53.

[10] 邢家省.法曲率最值的直接求法[J].吉首大学学报：自然科学版，2012，33(4)：11-15.

[11] 邢家省，王拥军.曲面上法曲率的最值和最值切方向的性质[J].吉首大学学报：自然科学版，2013，34(1)：6-10.

[12] 邢家省,张光照.曲面上曲线的测地曲率向量的注记[J].吉首大学学报：自然科学版，2013，34(4)：7-10.

[13] 邢家省，贺慧霞，高建全.求解指定第一和第二基本形式的曲面方程的方法[J].吉首大学学报：自然科学版,2013,34(6):4-8.

(责任编辑 向阳洁)

MatrixMethodofFundamentalEquationofCurvedSurface

XING Jiasheng1,GAO Jianquan2,LUO Xiuhua2

(1.Department of Mathematics,LMIB of the Ministry of Education,Beihang University,Beijing 100191，China;2.Pingdingshan Institute of Education,Pingdingshan 467000,He’nan China)

A method to deduce the curved surface structure equation from matrix equations is introduced.This method replaces complicated tensor mark relation with the matrix fundamental operation,so that the deducing process becomes easier and clearer.

fundamental equation of curved surface;curved surface structure equation;matrix multiplication;Gauss curvature

1007-2985(2014)03-0004-07

2013-07-20

国家自然科学基金资助项目(11201020)

邢家省(1964-)，男，河南泌阳人,北京航空航天大学数学与系统科学学院副教授,博士，主要从事偏微分方程、微分几何研究.

O186.1

A

10.3969/j.issn.1007-2985.2014.03.002