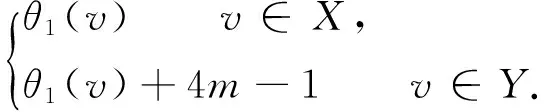非连通图C4m-1∪G的优美标号*

吴跃生

(华东交通大学基础科学学院,江西 南昌330013)

非连通图C4m-1∪G的优美标号*

吴跃生

(华东交通大学基础科学学院,江西 南昌330013)

讨论了非连通图C4m-1∪G的优美性，给出了非连通图C4m-1∪G是优美图的2个充分条件.

优美图;交错图；非连通图;优美标号

1 相关定义

文中所讨论的图均为无向简单图，V(G)和E(G)分别表示图G的顶点集和边集，记号[m,n]表示整数集合{m,m+1,…,n}，其中m和n均为非负整数，且满足0≤m

图的优美标号问题是组合数学中一个热门课题[1-11].

定义1[1]对于一个图G=(V,E)，若存在一个单射θ:V(G)→[ 0,|E(G)|]使得对所有边e=(u,v)∈E(G)，由θ′(e)=|θ(u)-θ(v)|导出的E(G)→[1,|E(G)|]是一个双射，则称G是优美图,θ是G的一组优美标号，称θ′为G的边上的由θ导出的诱导值.

定义2[1]设f为G的一个优美标号，若存在一个正整数k，使得对任意的uv∈E(G)有f(u)>k≥f(v)或f(u)≤k

显然，若f为G的平衡标号，则k是边导出标号为1的边的2个端点中标号较小的顶点的标号.

定义3[1]在平衡二分图G中，设其优美标号θ的特征为k，并且θ(u0)=k，θ(v0)=k+1，则称u0为G的二分点，v0为G的对偶二分点.

2 主要结果及其证明

定理1 对任意正整数m，若图G是特征为k且缺k+3m-1标号值的交错图(3m-1≤k+3m-1≤|E(G)|)，则非连通图C4m-1∪G存在缺标号值k+1的优美标号.

定义C4m-1∪G的顶点标号θ为：

θ(x2i)=4m-i+k,i=1,2,…,2m-1;θ(x2i-1)=i+k+1,i=1,2,…,m;

下面证明θ是非连通图C4m-1∪G的优美标号.

(ⅰ)θ:X→[0,k]是单射(或双射);θ:Y→[k+4m,q+4m-1]-{7m-2+k}是单射(或双射);θ:V(C4m-1)→[k+2,k+4m-1]∪{7m-2+k}是单射(或双射);θ:V(C4m-1∪G)→[0,q+4m-1]-{k+1}是单射.

(ⅱ)

θ′(x2m+2x2m+1)=4m-1；

θ′(x2mx2m+1)=4m-2；θ′(x4m-1x1)=2m-2.

θ′:E(C4m-1)→[1,4m-1]是双射；θ′:E(G)→[4m,q+4m-1]是双射.θ′：E(C4m-1∪G)→[1,q+4m-1]是一一对应.

由(ⅰ)和(ⅱ)可知，θ就是非连通图C4m-1∪G的缺k+1标号值的优美标号.证毕.

定理2 对任意正整数m，若图G是特征为k且缺k+m+1标号值的交错图(m+1≤k+m+1≤|E(G)|)，则非连通图C4m-1∪G存在缺标号值k+1,特征为2m+k+1的优美标号.

下面证明θ是非连通图C4m-1∪G的优美标号.

(ⅰ)θ:X→[0,k]，θ:Y→[k+4m,q+4m-1]-{k+5m}，θ:V(C4m-1)→[k+2,k+4m-1]∪{k+5m}均为单射(或双射);θ:V(C4m-1∪G)→[0,q+4m-1]-{k+1}为单射.

(ⅱ)

θ′(x2m-1x2m)=4m-1；

θ′(x2mx2m+1)=4m-2；θ′(x4m-1x1)=2m-1.

θ′:E(C4m-1)→[1,4m-1]，θ′:E(G)→[4m,q+4m-1]均为双射.θ′：E(C4m-1∪G)→[1,q+4m-1]是一一对应.

由(ⅰ)和(ⅱ)可知θ就是非连通图C4m-1∪G的缺k+1标号值的优美标号.证毕.

引理1 对任意正整数n，设C4n是有4n个顶点的圈，则C4n存在特征为2n-1且缺3n的交错标号.

容易验证，θ就是圈C4n的特征为2n-1且缺3n的交错标号.

注意到3n=(2n-1)+n+1，由定理1和引理1有以下结论：

推论1 对任意正整数m，非连通图C4m-1∪C12m-8存在缺标号值6m-4的优美标号.

例1 非连通图C7∪C16存在缺标号值8的优美标号为:非连通图C7∪C16中C7的优美标号为9,14,10,13,19,12,11,9;非连通图C7∪C16中C16的优美标号为0,23,1,22,2,21,3,20,4,18,5,17,6,16,7,15,0.

由定理2和引理1有以下结论：

推论2 对任意正整数m，非连通图C4m-1∪C4m存在缺2m标号值的优美标号.

例2 由推论2给出的非连通图C11∪C12的缺标号值6的优美标号为7,16,8,15,9,20,10,14,11,13,12,7;0,23,1,22,2,21,3,19,4,18,5,17,0.

[1] 马克杰.优美图[M].北京:北京大学出版社，1991.

[2] 杨显文.关于C4m蛇的优美性[J].工程数学学报，1995,12(4):108-112.

[3] 吴跃生.关于圈C4h的(r1,r2,…,r4h)-冠的优美性[J].华东交通大学学报,2011,28(1):77-80.

[4] 吴跃生,李咏秋.关于圈C4h+3的(r1,r2,…,r4h+3)-冠的优美性[J].吉首大学学报：自然科学版,2011,32(6):1-4.

[7] 吴跃生.图C7(r1,r2,r3,r4,r5,0,0)∪St(m)的优美性[J].吉首大学学报：自然科学版,2012,33(5):9-11.

[8] 吴跃生,王广富，徐保根.关于C4h+1⊙K1的(Gr1,Gr2,…,Gr4h+1,Gr4h+2)-冠的优美性[J].山东大学学报,2013，48(4)：25-27.

[9] 吴跃生.关于圈C4h+3的(Gr1,Gr2,…,Gr4h+3)-冠的优美性[J].吉首大学学报:自然科学版,2013,34(4):4-9.

[10] 吴跃生,王广富，徐保根.非连通图C2n+1∪Gn-1的优美性[J].华东交通大学学报,2012,29(6):26-29.

[11] GALLIAN J A.A Dynamic Survey of Graph Labeling[J].The Electronic Journal of Combinatorics，2013,16(DS6)：1-308.

(责任编辑 向阳洁)

GracefulLabelingoftheUnconnectedGraphC4m-1∪G

WU Yuesheng

(School of Basic Sciences,East China Jiaotong University,Nanchang 330013,China )

The gracefulness of the unconnected graphC4m-1∪Gis discussed.Two sufficient conditions are given for the gracefulness of unconnected graphC4m-1∪G.

graceful graph;balanced bipartite graph;unconnected graph;graceful labeling

1007-2985(2014)03-0001-03

2013-10-25

国家自然科学基金资助项目(11261019,11361024)；江西省自然科学基金资助项目(20114BAB201010)

吴跃生(1959-)，男，江西瑞金人，华东交通大学基础科学学院副教授，硕士，主要从事图论研究.

O157.5

A

10.3969/j.issn.1007-2985.2014.03.001