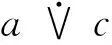上连续完备模格的半单性*

牛娟宁,黎奇升

(吉首大学,湖南 吉首 416000)

上连续完备模格的半单性*

牛娟宁,黎奇升

(吉首大学,湖南 吉首 416000)

对于上连续完备模格L,证明了L是局部原子格等价于1是原子的并,也等价于1是独立原子的并,并进一步给出了1可分解为有限个原子并的若干等价条件.

完备格;半单性;独立子集;紧生成;上连续

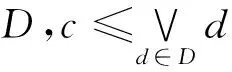
1 独立集的基本性质

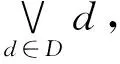
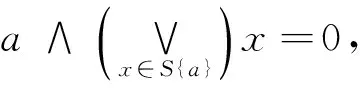
命题1 设L是上连续的完备模格，S⊆L{0}，则S是独立的当且仅当S是弱独立的.

证明必要性是显然的，下证充分性.

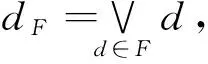
引理1 设L为完备模格，S⊆L{0}，则S是弱独立的当且仅当S的任意子集是弱独立的.

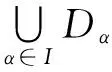
命题2 设L为上连续的完备模格，Ø≠S⊆L{0}，则S包含极大弱独立子集.

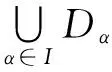
命题4 设L为完备模格,D为L的弱独立子集，则对任意彼此不同的元素ai,bj∈D(i=1,2，…，n;j=1,2，…，m),有

(1)

证明施数学归纳法于n.

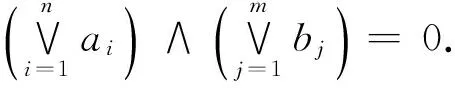
2 完备模格的直并分解

定义2 设L为完备格，若1为原子的并，则称L为半单格.

引理3[3]设L为上连续的完备格，则L的原子是紧的.

引理4[3]设L为模格，a,b∈L,则区间格[a∧b,a]与区间格[b,∨b]同构.

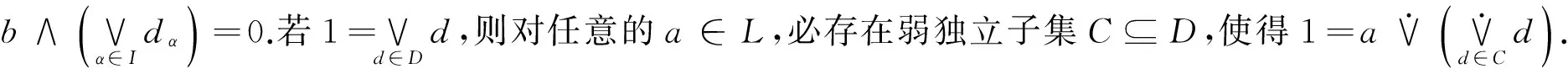
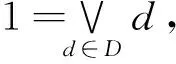
在命题5中令a=0即可得推论2.

推论3 设L为上连续的完备模格，若L为半单格，则L是可补的.

作为直接推论，立得如下结果：

推论4[3]设L为上连续的完备模格，若L为局部原子格，则L是可补的.

定理1 设L为上连续的完备模格，则有:(ⅰ)L是半单的当且仅当L是局部原子格；(ⅱ)若L是半单的，则L是紧生成的.

证明(ⅰ)充分性是显然的，下证必要性.

(ⅱ)因L是上连续的,由引理3知每一个原子是紧的,据(ⅰ)知L是紧生成的.

以下例子说明推论2去掉条件“上连续”后不再成立，定理1去掉“上连续”与“模格”2个条件中的一个后不再成立.

例1 设N为正整数集，令L=N∪{∞}.对∀m,n∈L,定义m≤n当且仅当n=∞，或m,n∈N并且m整除n,则有:(ⅰ)≤是L上的偏序关系;(ⅱ)L关于该偏序关系作成模格且最大元为∞,最小元为整数1;(ⅲ)L不是上连续的格；(ⅳ)n是L的原子当且仅当n是素数；(ⅴ)L是半单的但不是局部原子格;(ⅵ)L不是可补的.

例2 设L={1,2,4,3,12},对∀m,n∈L，m≤n当且仅当m整除n，则有:(ⅰ)≤是L上的偏序关系;(ⅱ)L关于该偏序关系作成上连续的格;(ⅲ)L不是模格;(ⅳ)L是半单的但不是局部原子格.

命题6 设L为可补的完备模格，0≠a∈L，若a是紧元素的并，则存在原子c0≤a.

设x∈L,且x

命题6的证明蕴含了如下结论：

推论5 设L为可补的完备模格，0≠a∈L为紧元素的并，则区间格[0,a]有极大元.

定理2 设L是完备模格,则以下几条等价：(ⅰ)L是上连续的半单格；(ⅱ)L是上连续的且1是独立原子集的并；(ⅲ)L是上连续的且L是局部原子格；(ⅳ)L是紧生成且可补的；(ⅴ)L是紧生成的局部原子格.

证明据推论2知(ⅰ)⟺(ⅱ).据定理1有(ⅰ)⟺(ⅲ)，且(ⅲ)⟹(ⅴ)成立.因紧生成的格是上连续的，据命题5知，(ⅴ)⟹(ⅳ)成立.

命题7 设L为完备模格，a∈L.(ⅰ)若a是紧的，则a是有限生成的；(ⅱ)若L是上连续的，a是有限生成的，则a是紧的.

(ⅱ)见文献[6]定理2.

命题8 设L为上连续的完备模格.若L是紧致的和可补的,则L是半单的,且1是有限个独立原子的并.

定理3 设L为上连续的完备模格,则以下几条等价：(ⅰ)1是有限个原子的并；(ⅱ)1是有限个独立原子的并；(ⅲ)L是紧致的并且是可补的;(ⅳ)L是可补的且1是有限生成的；(ⅴ)L是紧致的并且不含真的本质元；(ⅵ)L不含真的本质元且1是有限生成的；(ⅶ)L每一个非零元是有限个原子的并；(ⅷ)L每一个非零元是有限个独立原子的并.

证明由推论2知(ⅰ)⟹(ⅱ)成立.由命题7知(ⅲ)⟺(ⅳ)与(ⅴ)⟺(ⅵ).(ⅲ)⟹(ⅴ)显然成立.

(ⅲ)⟹(ⅰ).格L为紧致上连续有补的完备模格，根据命题8知L是半单的,且1是有限个原子的并.

仿定理1(ⅰ)的证明知(ⅱ)⟺(ⅷ).∀0≠a∈L，应用推论2于子格[0,a]可知，(ⅶ)⟺(ⅷ)成立.

由文献[3]，格L称为Noether的，如果L的任意非空子集有极大元.不难验证Noether格是上连续的且每个元素是有限生成的，于是有下面的推论：

推论6 设L为Noether完备模格，则以下几条等价：(ⅰ)1是有限个原子的并；(ⅱ)1是有限个独立原子的并；(ⅲ)L每一个非零元是有限个原子的并；(ⅳ)L每一个非零元是有限个独立原子的并；(ⅴ)L是可补的；(ⅵ)L不含真的本质元.

注2 因格L具有有限长度当且仅当L既是Neother的又是Artin的，故由推论6可立得文献[4]的主要结果.

[1] ANDERSON F W,FULLER K R.Rings and Categories of Modules[M].Berlin Heidelberg,New York:Springer Verlag,1974.

[2] 刘绍学.环与代数[M].北京：科学出版社，1982.

[3] BO STENST M.Rings of Quotients[M].Berlin Heidelberg,New York:Springer Verlag,1975.

[4] 张 霞,陈裕群.模格与半单代数[J].华南师范大学学报:自然科学版,2004(2):20-25.

[5] GRATZER G.General Lattice Theory[M]//Pure and Applied Math. Series.New York:Academic Press,1978.

[6] 庹 清,罗慧明.关于具有0,1元素的格[J].吉首大学学报:自然科学版,1999,20(1):34-36.

(责任编辑 向阳洁)

SemisimplicityforUpperContinuousandCompleteModularLattices

NIU Juanning,LI Qisheng

(College of Mathematics and Statics,Jishou University,Jishou 416000,Hunan China)

It is proved that for an upper continuous and complete modular latticeL,Lis locally atomic if and only if 1 is a join of atoms,and if and only if 1 is a join of independent atoms.Moreover,some conditions under which 1 can be expressed as a join of finite atoms are given.

complete lattice;semi-simplicity;independent set;compactly generated;upper continuous

1007-2985(2014)05-0013-05

2014-04-15

湖南省研究生创新科研基金资助项目(CX2014B434)；吉首大学校级课题资助项目(14JDY049)

牛娟宁(1987—),女,陕西宝鸡人,吉首大学基础数学专业硕士研究生，主要从事同调代数研究;黎奇升(1964-),男,湖南张家界人,吉首大学教授，博士,主要从事同调代数与K-理论研究.

O153.1

A

10.3969/j.issn.1007-2985.2014.05.004