测度链上次线性二阶Hamilton系统周期解的存在性*
2014-09-06张申贵
张申贵
(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)
测度链上次线性二阶Hamilton系统周期解的存在性*
张申贵
(西北民族大学数学与计算机科学学院,甘肃 兰州 730030)
研究测度链上非自治二阶Hamilton系统周期解的存在性问题.在非线性项次线性增长时,将这类系统的周期解转化为定义在一个适当空间上泛函的临界点,然后利用临界点理论建立了此类系统周期解的存在性结果.
测度链上系统;周期解;次线性;临界点理论
1 问题的提出
德国学者Hilger在其博士论文中提出了测度链分析理论,这种理论将连续分析和离散分析结合在一起,实现了数学理论方面的大突破.所谓测度链是指实数集R的任意非空子集,通常用“T”来表示,“T”可以是R、Z、R+、Cantor集、闭区间的并集等.
测度链上动力方程广泛地应用于生物系统、金融分析、疾病控制等领域中出现的数学模型.例如,美国学者Peterson和Thomas利用测度链上的动力方程弥合了西尼罗河病毒传播的差分方程模型和微分方程模型之间的空隙,并建立了更为全面和实用的数学模型.
测度链上动力方程的基础理论可参见文献[1-2].近年来,许多学者研究了测度链上边值问题解的存在性[3-8],所用的工具为锥上的不动点定理.从2009年开始,临界点理论被用来研究测度链上边值问题解的存在性.文献[9]研究了变号位势下测度链上二阶Hamilton系统周期解的存在性;当具有次二次或超二次位势时,文献[10-12]得到了测度链上二阶Hamilton系统周期解存在的充分条件.
考虑测度链上二阶Hamilton系统
(1)
周期解的存在性.其中:T>0;ρ(t)为后跳跃算子;H(t,u)=DuH(t,u);[0,T]T表示[0,T]∩T;H:[0,T]T×RN→R满足对每个x∈RN,H(t,x)关于t可测,对Δ-a.e.t∈[0,T]T,H(t,x)关于x连续可微,且存在a∈C(R+,R+),b∈L1([0,T]T;R+),使得|H(t,x)|≤a(|x|)b(t),|H(t,x)|≤a(|x|)b(t)对所有x∈RN和Δ-a.e.t∈[0,T]T成立.
若T=R,则系统(1)为二阶Hamilton系统:

若T=Z,T≥2,则系统(1)为二阶离散Hamilton系统:
其中Δu(t)=u(t-1)-u(t),Δ2u(t)=Δ(Δu(t)).
笔者将研究次线性条件下测度链上二阶Hamilton系统(1)的周期解,利用临界点理论中的鞍点定理建立系统(1)周期解存在性的新结果.
2 预备知识
定义1 称实数集R的任意非空子集为测度链(或时间标架),通常用“T”来表示.
定义2 对于t∈T,定义向前跳跃算子σ:T→T为σ(t)=inf{τ∈T:τ>t},定义向后跳跃算子ρ:T→T为ρ(t)=sup{τ∈T:τ
此外,若T有右稀的最小值m,则定义Tκ=T-{m},否则,Tκ=T.若T有左稀的最大值M,则定义Tκ=T-{M},否则,Tκ=T.
定义3 假设f:T→R,t∈Tκ.若存在一个实数θ,使得对于∀>0,存在t的一个开领域U,对于所有的s∈U,都有|f(o(t))-f(s)-θ(σ(t)-s)|≤|σ(t)-s|成立,则称f在t点是Δ-可微的,称θ为f在t点的Δ-导数,记为θ=fΔ(t).若对于所有的t∈Tκ,f在t点都是Δ-可微的,则称f在Tκ上是Δ-可微的.
若T=R,则fΔ(t)=f′(t);若T=Z,则fΔ(t)=Δf(t).

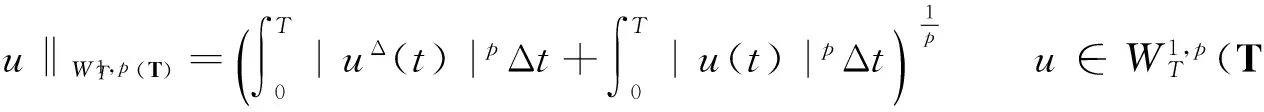
此外,设
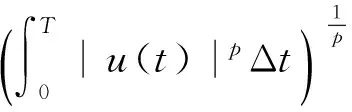
‖u‖∞≤C0‖u‖.
(2)
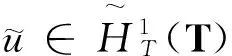
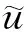
(3)
φ′(u),v=(uΔ(t),vΔ(t))Δt-(H(t,u(t)),v(t))Δt∀u,v∈(T).
定义5 设X为Banach空间,若泛函φ∈C1(X,R)满足对任何点列{un}⊂X,由{φ(un)}有界,φ′(un)→0蕴含{un}有收敛子列,则称泛函φ满足(PS)条件.

3 主要结果及其证明
定理1 设存在f,g∈L1([0,T]T;R+),0<α<1,使得
|H(t,x)|≤f(t)|x|α+g(t),
(4)
对所有x∈RN和Δ-a.e.t∈[0,T]T成立,且满足
(5)

注1 (4)式表明非线性项H(t,x)关于变量x是次线性增长的.当极限值为+∞时,(5)式为著名的Ahmad-Lazer-Paul型强制性条件.
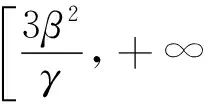
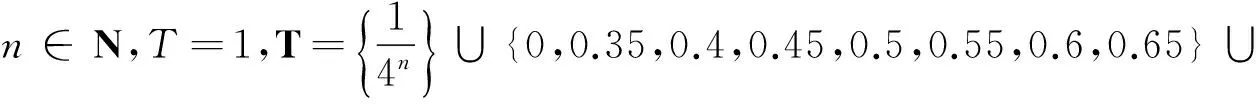


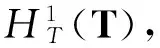
|φ(un)|≤cφ′(un)→0,n→∞
(6)


由(2),(4)式,有

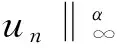
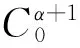
(7)
由(3),(6),(7)式,有
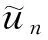

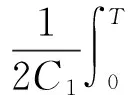

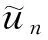
(8)
由(8)式可得
(9)
由(9)式,并注意到0<α<1,当n→∞时,有

(10)
由(7),(9)式,有



(11)
由(2),(4),(9)式,有
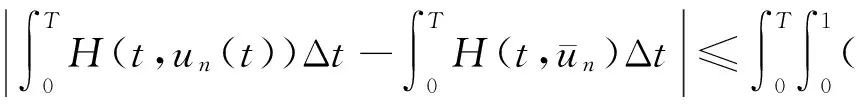





(12)

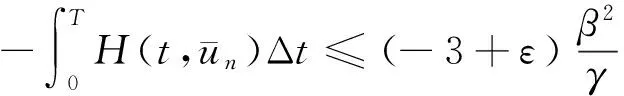
(13)
由(11),(12),(13)式,有



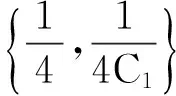
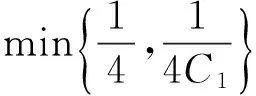
由0<α<1知,当‖u‖→+∞时,φ(u)→+∞.显然存在常数ω,使得φ(u)≥ω.令e=0,则引理1中(ⅰ)成立.
另一方面,对y∈E1=RN,由(5)式,对∀ε>0,当‖y‖充分大时,有

令ε充分小,当‖y‖→+∞时,φ(y)→-∞.因此存在正常数ρ,使得φ|∂Bρ∩E1≤ω-1=σ,则引理1中(ⅱ)成立.
[1] MARTIN BOHNER,ALLAN C PETERSON.Dynamic Equations on Time Scales:An Introduction with Applications[M].Boston:Birkhäuser,2001.
[2] MARTIN BOHNER,PETERSON A.Advances in Dynamic Equations on Time Scales[M].Boston:Birkhäuser,2003.
[3] LI Wantong,SUN Hongrui.Multiple Positive Solutions for Nonlinear Dynamic Systems on a Measure Chain[J].J. Comput. Appl. Math.,2004,162:421-430.
[4] SUN Jianping,LI Wantong.Positive Solution for System of Nonlinear First-Order PBVPs on Time Scales[J].Nonlinear Anal.,2005,62:131-139.
[5] SUN Jianping,LI Wantong.Existence of Positive Solutions to Semipositone Dirichlet BVPs on Time Scales[J].Dynammics Systems Applications,2007,16:571-578.
[6] SU Youhui,LI Wantong.Triple Positive Solutions ofm-Point BVPs forp-Laplacian Dynamic Equations on Time Scales[J].Nonlinear Anal.,2008,69:3 811-3 820.
[7] RYNNE B P.L2Spaces and Boundary Value Problems on Time-Scales[J].J. Math. Anal. Appl.,2007,328:1 217-1 236.[8] ZHANG Hongtao,LI Yongkun.Existence of Positive Periodic Solutions for Functional Differential Equations with Impulse Effects on Time Scales[J].Communications in Nonlinear Science and Numerical Simulation,2009,14(1):19-26.
[9] SU Youhui,LI Wantong.Periodic Solution of Second-Order Hamiltonian Systems with a Change Sign Potential on Time Scales[J].Discrete Dynamics in Nature and Society,2009,13:1-17.
[10] SU Youhui,LI Wantong.Periodic Solution for Non-Autonomous Second Order Hamiltonian Systems on Time Scales[J].Dynamic Systems and Applications,2009,18:621-636.
[11] SU Youhui,FENG Zhaosheng.A Nonautonomous Hamiltonian System on Time Scales[J].Nonlinear Anal.,2012,75(10):4 126-4 136.
[12] ZHOU Jianwen,LI Yongkun.Variational Approach to a Class of Second Order Hamiltonian Systems on Time Scales[J].Acta. Applicandae Mathematicae,2012,117(1):47-69.
[13] MAWHIN J,WILLEM M.Critical Point Theory and Hamiltonian Systems[M].New York:Springer-Verlag,1989.
[14] LI Yongkun,ZHOU Jianwen.Existence of Solutions for a Class of Damped Vibration Problems on Time Scales[J].Advances in Difference Equations,2010,27:1-27.
(责任编辑 向阳洁)
PeriodicSolutionforSublinearNon-AutonomousSecondOrderHamiltonianSystemsonTimeScales
ZHANG Shengui
(College of Mathematics and Computer Science,Northwest University for Nationalities,Lanzhou 730030,China)
The existence of periodic solutions for non-automous second order Hamiltonian systems on time scales with sublinear nonlinearity is investigated.The periodic solutions of the system are converted into the critical points of a functional defined on a proper space,and the existence of periodic solutions is proved by critical point theory.
Hamiltonian systems on time scales;periodic solution;sublinear;critical point theory
1007-2985(2014)05-0001-05
2014-03-18
国家自然科学基金资助项目(31260098);中央高校基本科研业务费专项资助项目(31920130004)
张申贵(1980—),男,甘肃兰州人,西北民族大学数学与计算机科学学院副教授,主要从事非线性泛函分析研究.
O175.12
A
10.3969/j.issn.1007-2985.2014.05.001
