Dynamical chiral symmetry breaking in QED3
2014-09-06ZhouYuqing
Zhou Yuqing
(Department of Physics, Southeast University, Nanjing 211189, China)
Dynamical chiral symmetry breaking in QED3
Zhou Yuqing
(Department of Physics, Southeast University, Nanjing 211189, China)
In order to examine how a propagator behaves in non-perturbative theories and how its behavior is influenced by the choice of a covariant gauge, a truncated Dyson-Schwinger equation is used to numerically investigate the properties of fermions and bosons in 3D quantum electrodynamics(QED), and a series of self-consistent solutions for the fermion propagator in the Nambu and Wigner phases are obtained. These numerical solutions show that the propagator behaves very differently in the Landau gauge domain and in the infrared energy region outside it. By using the propagators in the Nambu and Wigner phases under various gauges, it is further investigated how the fermion equivalent pressure difference and fermion condensation change with the gauge parameters. These results indicate that the phase transition described by the CJT equivalent potential and the chiral phase transition described by the chiral condensation are not completely identical.
propagator; covariant gauge; 3D quantum electrodynamics(QED); equivalent pressure difference; fermion condensation; chiral phase transition
Gauge fields play a basic role in particle physics. According to theoretical physics, all the physical results should be independent of the gauge parameter. The results show this to be true at every level of approximation in perturbation theory, while this has not been successfully demonstrated in general in the non-perturbative case. Within the framework of strong correlation, the system shows dynamical chiral symmetry breaking (DCSB), where the massless fermion gains a nonzero mass. In addition, all of the information about the system can be obtained from the propagators. Therefore, it is necessary to study the idiographic behavior of propagators and the influence of the covariant gauge on behavior in a non-perturbative theory.
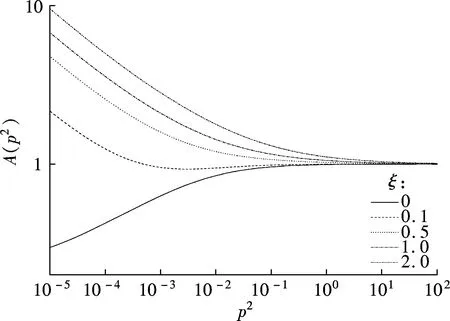
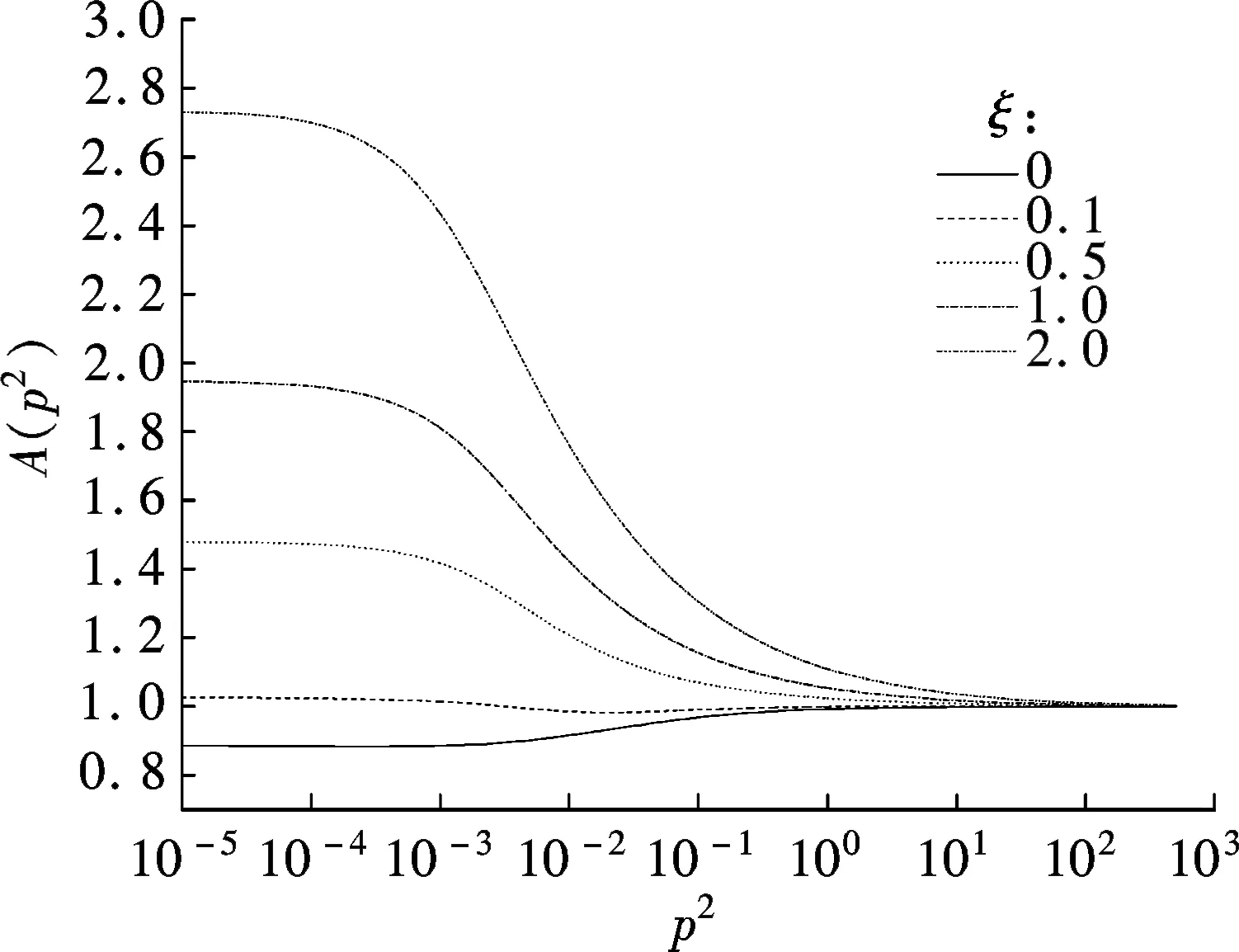
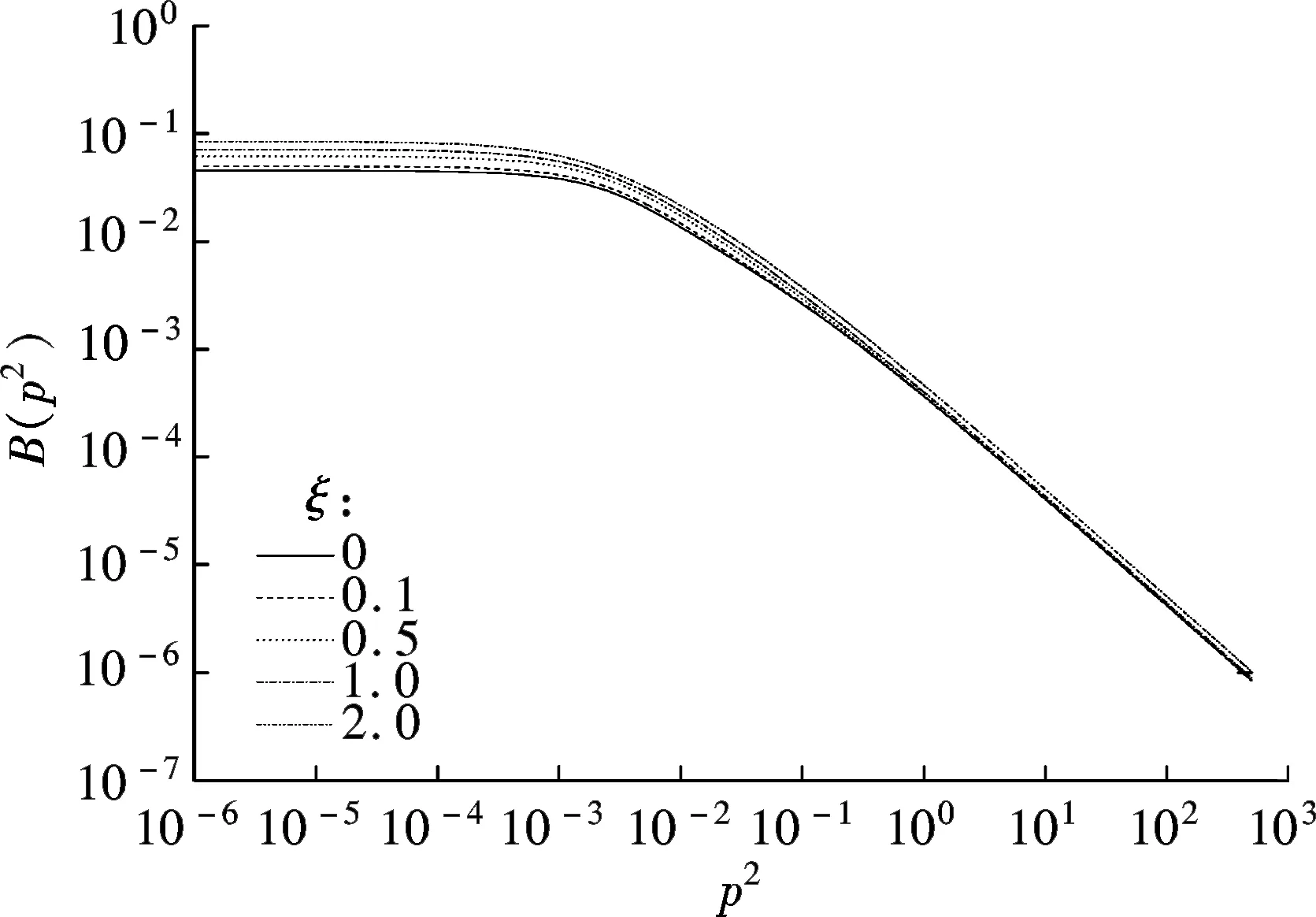
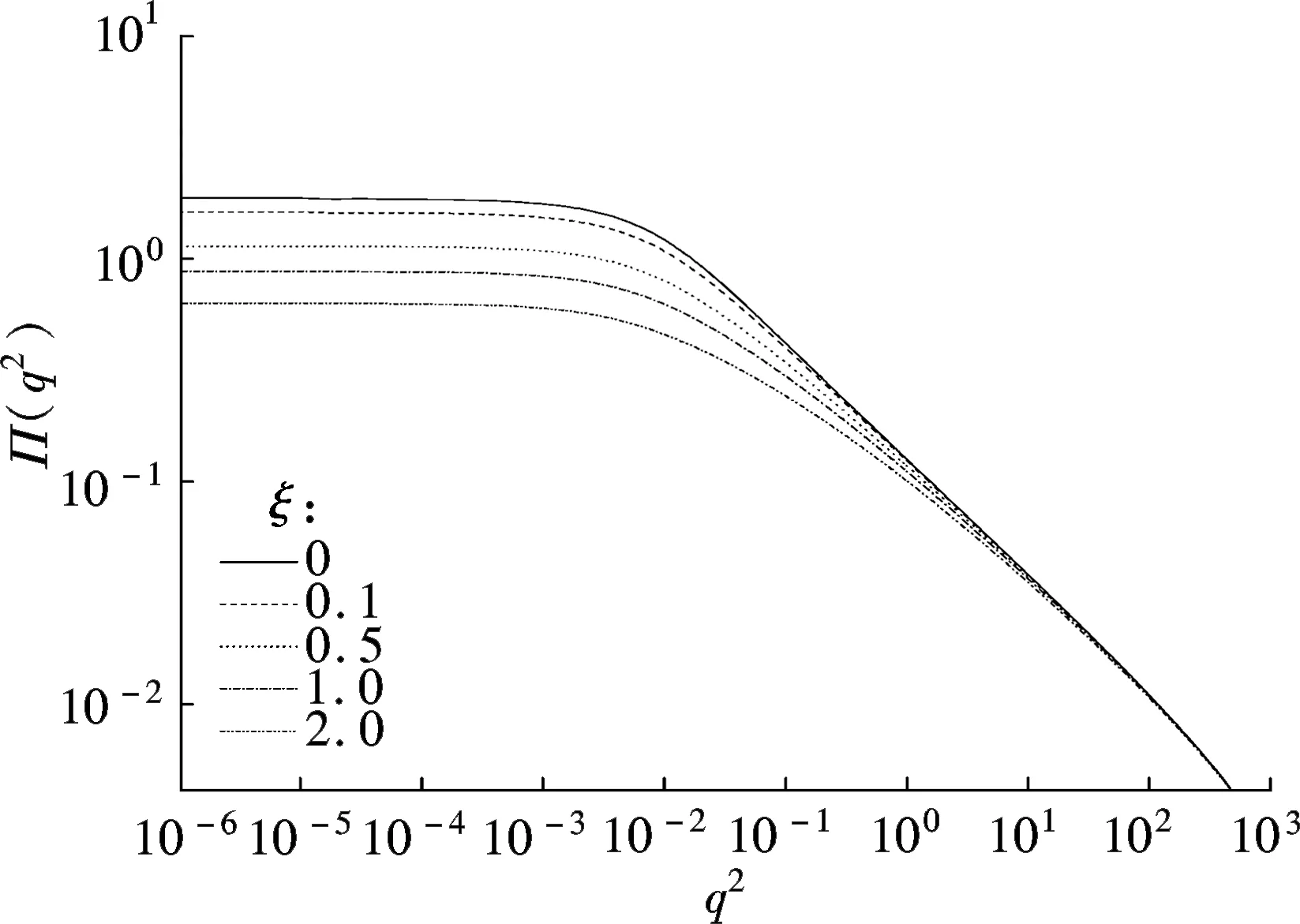
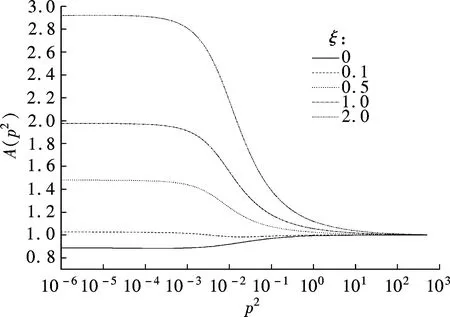
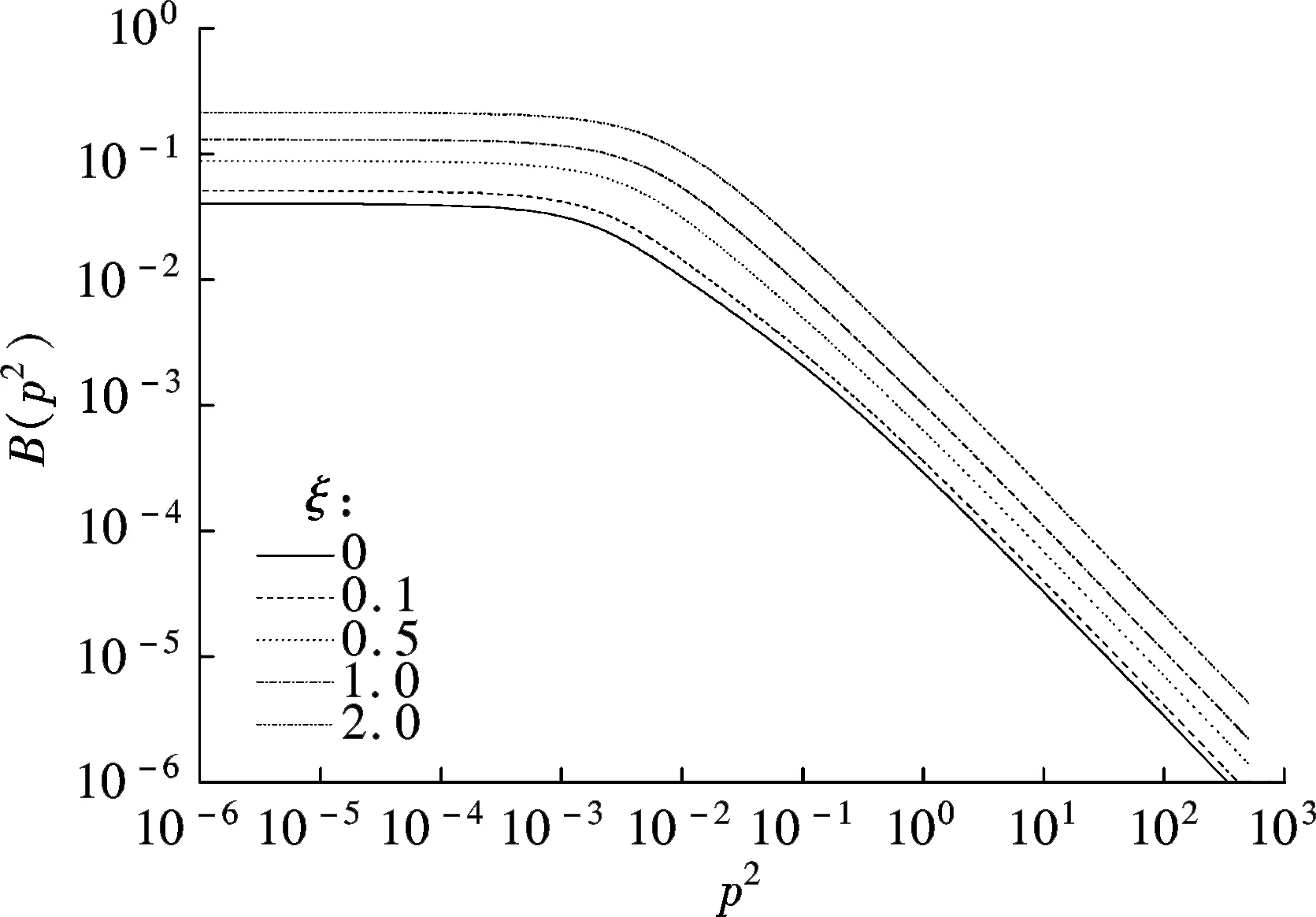
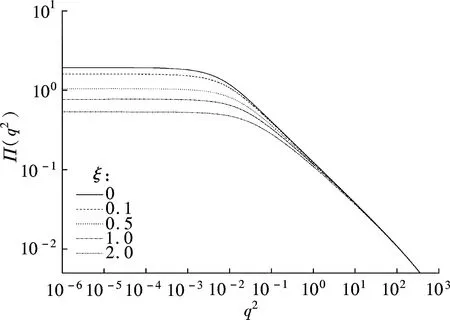
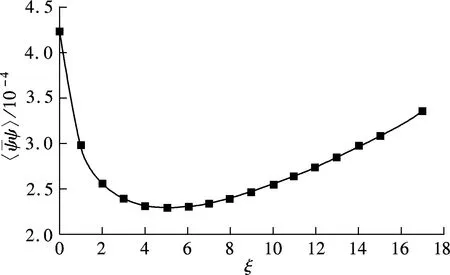
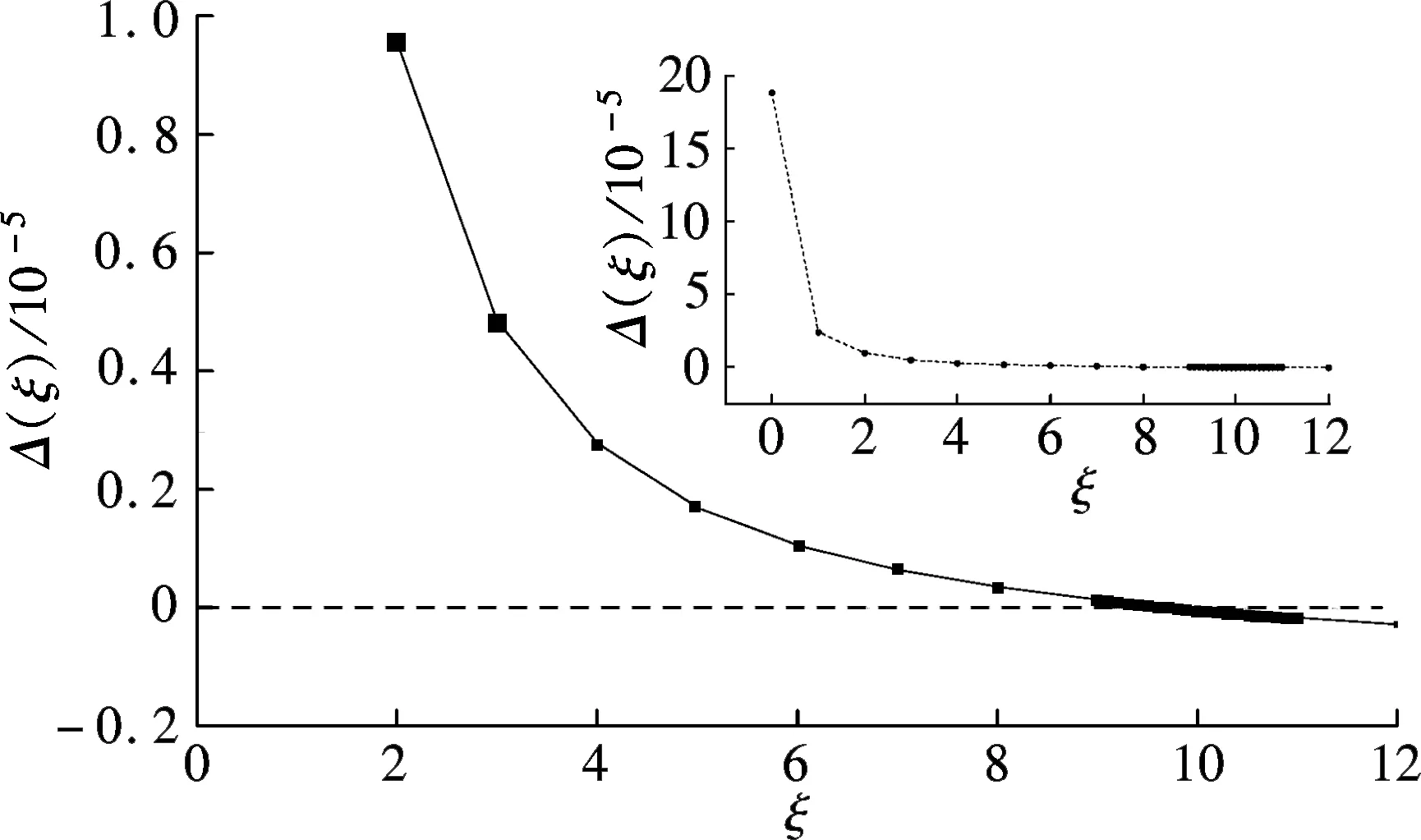
To understand the propagators, we invoke the Dyson-Schwinger (DS) equations for fermion and boson propagators. As is well known, there are two solutions for the DS equations for the fermion propagator, namely, the Nambu and Wigner solutions. In the chiral limit, the Nambu solution corresponds to the chirally broken phase while the Wigner solution corresponds to the chirally symmetric phase. We believe that the Nambu solution is the solution that is realized in the real world. Several studies[1-3]have shown that the Nambu solution occurs only with fermion flavorsNless than a critical valueNc, but none of them has shown the Wigner solution atN (1) whereξis the covariant gauge parameter. We use four-component spinors for the fermions, and accordingly, a four-dimensional representation for theγmatrices. QED3has many features similar to QCD in 3+1 dimensions. QED3is known to have a phase where the initial chiral symmetry of the theory is spontaneously broken, and it is also known that the fermions are confined to this phase. Moreover, QED3is super-renormalizable, and we can, therefore, avoid the ultraviolet divergences that are present in QED4. These are the basic reasons why QED3is regarded as an ideal toy model for non-perturbative theory. QED3is a possible candidate for the study of DCSB[1-13]and confinement[14-16]within a theory that is structurally much simpler than QCD, while sharing the same basic non-perturbative phenomena. Since the Dyson-Schwinger (DS) equations provide a powerful tool for resolving the propagators in non-perturbative theory, these coupled equations in QED3can be used to investigate our problem. From the Lagrangian (1) and DS equations for the fermion propagator, we derive (2) S-1(p)=iγ·pA(p2)+B(p2) (3) and obtain a function for wave-renormalizationA(p2), (4) and the fermion self-energyB(p2), (5) In addition, the DS equation satisfied by the polarization tensor for a photon is given by (6) The corresponding full photon propagator in a covariant gauge is (7) with the vacuum polarizationΠ(q2) defined by Πρν(q2)=(q2δρν-qρqν)Π(q2) (8) This vacuum polarization tensor has an ultraviolet divergence which is present only in the longitudinal component and can be removed by applying the projection operator (9) to project a finite value of vacuum polarization for it,Π(q2)[17]. In principle, we can obtain the fermion and boson propagators from these coupled equations. Nevertheless, it is too complex to solve the DS equations because the necessary full fermion-photon vertexΓν(p,k) is unknown. Although several studies have attempted to resolve this problem, none are completely satisfactory[4,7-10,18-22]. 1.1 The rainbow approximation The simplest scheme for truncating the DS equation is the rainbow approximation. This structure plays the most dominant role in the full vertex in the high energy region and the full fermion-boson vertex reduces to it in a large momentum limit. Due to the complexity of QCD, many works on hadron physics have adopted this ansatz to analyze low energy behavior. We make use of it, although the tensor destroys the Ward-Takahashi identity (WTI). The pivotal functions for the propagators can then be written as (10) (11) (12) wherep=q+kandξ′(q2)=ξ[1+Π(q2)]. 1.2 Beyond the bare vertex Therefore, we write the truncated DS equations for propagators in a covariant gauge as follows: (13) (14) (15) First, we work within the Landau gauge. From the above DS equations for the fermion propagator, we find that the self-energy function has one trivial solution, i.e., the Wigner solution (B(p2)≡0). In the corresponding phase, the fermion remains massless and chiral symmetry is restored. Setting the original value ofB(p2)=0 andA(p2)=1,Π(q2)=1 in the rainbow approximation, we iterate the coupled functions to find stable results, and show these in Fig.1. (a) (b) The line in Fig.1 shows that the vector function of the inverse fermion propagator diminishes asp2→0, while the polarization of the boson reaches infinity asq2→0. Nevertheless, settingA(p2)=1 andΠ(q2)=1 reduces the single-iteration results at large momenta. This is because QED3is asymptotically free andS(p)→S0(p) in the high energy region. In addition to the Landau gauge, we also give the behavior of the propagators at several values ofξin Fig.1. It is shown that the behaviors of both the fermion and boson propagators here are different from those in the Landau gauge, whereA(p2) is divergent in the infrared limit. Asξis increased,A(p2) increases more and more rapidly whenp2decreases. Correspondingly,Π(q2) gives the opposite trend forξand, for a particular value ofξ, is not divergent and remains almost constant in the infrared region. Moving beyond the rainbow approximation and following the above method, we obtainA(p2),Π(q2) and show them in Fig.2. It is shown that, compared with the bare approximation, the truncated scheme changes the value of solutions at a fixedp2in the infrared region, but apparently does not change the gauge dependence of the fermion or boson propagator behavior. (a) (b) We next consider the Nambu phase. Eqs.(11) and (14) have nontrivial solutions whenB(p2)≠0. The original fermion acquires dynamical mass through the non-perturbative effect. We solve the coupled equations numerically for Eqs.(10) to (15) at several values ofξ. Starting withA(p2)≡1,B(p2)≡1, andΠ(q2)≡1, we iterate the three coupled equations until all three functions converge to a stable solution. The typical behavior of the three functionsA,B, andΠin the Nambu phase are plotted in Fig.3 in the rainbow approximation and Fig.4 by application of theBC1vertex. For a value ofξ, it is apparent that all three functions are almost constant in the low energy region. (a) (b) (c) Within a range of values ofξ, the infrared value ofA(p2) increases with the increase inξ. Correspondingly, the numerical results show a reversed trend for the infrared value of fermion self-energy and boson polarization withξin each truncated scheme for the DS equation. Nevertheless, the behavior ofA(p2) orΠ(q2) is independent ofξin the high energy region. However, compared with the rainbow approximation,B(p2), which is given beyond the rainbow approximation, appears to depend onξ. Certainly, for any value ofξ, a different truncated scheme has similar behavior but dissimilar numerical values for the three functions in the infrared region. (a) (b) (c) Comparing the two phases, we also find thatA(0)<1 in the Nambu phase corresponds to its infrared zero value in the Wigner phase, whileA(0) diverges in the Wigner phase whenΠ(0) reaches a finite value in this covariant gauge theory. The fermion condensate is defined trivially as (16) In principle, this physical value is independent of the gauge parameter[25-27]. Adopting the above Nambu phase results for the rainbow approximation, we obtain the fermion condensate values and plot them in Fig.5. We find that the value appears to depend on the gauge parameter consequently. Fig.5 Gauge dependence of the condensate in the rainbow approximation It is easily proved that the rainbow approximation destroys the Ward-Takahashi identity. However, although the value in this figure depends onξ, we see that this condensate is always larger than zero and we learn that the chiral symmetry is broken. On the other hand, the Wigner solution gives zero fermion condensate and the chiral symmetry is restored. For anyξ, the Nambu and Wigner solutions are obtained from the same DS equations. The solution that is realized in the real world should be determined. We should compare the effective pressurePbetween the two phases, and the physical one will correspond to the largerPvalue. The effective pressure is given by[28] (17) Since theΓ2is known only in the rainbow approximation andΓ2=0, we adopt the first term in the last equation to study the phase transition. To indicate the real phase, we define the order parameterΔ=PN-PW. It is found that with the increase inξ,Δdecreases and becomes less than 0 whenξreaches the valueξp=9.8(see Fig.6). Based on the truncated DS equations applied to the fermion propagator, we have found solutions for both the fermion and boson propagators for several covariant gauges in the Nambu and Wigner phases. Numerical results show that the gauge parameter appears to affect the behavior of the fermion and boson propagators in the low energy region. Apart from the fermion self-energy, the other two functions are minimally affected in the high energy regions for both phases. Fig.6 Order parameter at different ξvalues In addition to the Landau gauge, the DS equations also provide the monotonic functions forA(p2) andΠ(q2) at several values ofξ. To the best of current knowledge, beyond the Landau gauge, the solutions for the fermion and boson propagators in the Wigner phase are presented in this paper for the first time. With the increase inξ, the infrared value ofAchanges from being zero to a divergent function, while the infrared value ofΠreduces to a constant that decreases withξbut does not completely diminish. We argue that there may be a value ofξfor which the infrared value ofAlies between zero and infinity. However, this value ofξhas not been found in the familiar gauge selected. In addition, the effective potential gives a different result around the chiral phase transition from the condensate, which implies that the two order parameters for the chiral phase transition might be self-inconsistent. [1]Appelquis T, Nash D, Wijewardhana L C R. Critical-behavior in (2+1)-dimensional QED[J].PhysicalReviewLetters, 1988, 60(25): 2575-2578. [2]Nash D. Higher-order corrections in (2+1)-dimensional QED[J].PhysicalReviewLetters, 1989, 62(26): 3024-3026. [3]Maris P. Influence of the full vertex and vacuum polarization on the fermion propagator in (2+1)-dimensional QED[J].PhysicalReviewD, 1996, 54(6): 4049-4058. [4]Burden C J, Roberts C D. Light-cone regular vertex in 3-dimensional quenched QED [J].PhysicalReviewD, 1991, 44(2): 540-550. [5]Pisarski R D. Chiral-symmetry breaking in 3-dimensional electrodynamics[J].PhysicalReviewD, 1984, 29(10): 2423-2426. [6]Appelquist T W, Bowick M, Karabali D, et al. Spontaneous chiral-symmetry breaking in 3-dimensional QED[J].PhysicalReviewD, 1986, 33(12): 3704-3713. [7]Atkinson D, Johnson P W, Maris P. Dynamic mass generation in 3-dimensional QED-improved vertex function[J].PhysicalReviewD, 1990, 42S(2): 602-609. [8]Curtis D C, Pennington M, Walsh D. Dynamics mass generation in QED3and the 1/Nexpansion[J].PhysicsLettersB, 1992, 295(3/4):313-319. [9]Kondo K, Nakatani H. Cutoff dependence of self-consistent solutions in unquenched QED3[J].ProgressofTheoreticalPhysics, 1992, 87(1):193-206. [10]Bashir A, Raya A. Landau-Khalatnikov-Fradkin transformations and the fermion propagator in quantum electrodynamics[J].PhysicalReviewD, 2002, 66(10):105005. [11]Bashir A. Non-perturbative fermion propagator for the massless quenched QED3[J].PhysicsLettersB, 2000, 491(3/4):280-284. [12]Liu G Z, Cheng G. Effect of gauge boson mass on chiral symmetry breaking in three-dimensional QED[J].PhysicalReviewD, 2003, 67(6), 065010. [13]Feng H T, Sun W M, Hu F, et al. The influence of the gauge boson mass on the critical number of the fermion flavors in QED(3)[J].InternationalJournalofModernPhysicsA, 2005, 20(13):2753-2762. [14]Burden C J, Praschifka J, Roberts C D. Photon polarization tensor and gauge dependence in 3-dimensional quantum electrodynamics[J].PhysicalReviewD, 1992, 46(6):2695-2702. [15]Maris P. Confinement and complex singularities in 3-dimensional QED[J].PhysicalReviewD, 1995, 52(10): 6087-6097. [16]Herbut I F, Seradjeh B H. Permanent confinement in the compact QED3with fermionic matter[J].PhysicalReviewLetters, 2003, 91(17):171601. [17]Burden C J, Praschifka J, Roberts C D. Photon polarization tensor and gauge dependence in 3-dimensional quantum electrodynamics[J].PhysicalReviewD, 1992, 46(6): 2695-2702. [18]Fischer C S, Alkofer R, Dahm T, et al. Dynamical chiral symmetry breaking in unquenched QED3[J].PhysicalReviewD, 2004, 70(7):073007. [19]Simmons E H. Useful gauges for studying dynamic fermion mass generation in arbitrary space-time dimension[J].PhysicalReviewD, 1990, 42(8): 2933-2935. [20]Kondo K I, Maris P. First-order phase-transition in 3-dimensional QFD with chern-simons term[J].PhysicalReviewLetters, 1995, 74(1):18-21. [21]Gusynin V P, Hams A H, Reenders M. (2+1)-dimensional QED with dynamically massive fermions in vacuum polarization[J].PhysicalReviewD, 1996, 53(4):2227-2235. [22]King J E. Transverse vertex and gauge technique in quantum electrodynamics[J].PhysicalReviewD, 1983, 27(8):1821-1829. [23]Curtis D C, Pennington M R. Truncating the Schwinger-Dyson equations: how multiplicative renormalizability and the ward identity restrict the 3-point vertex in QED[J].PhysicalReviewD, 1990, 42(12): 4165-4169. [24]Ball J S, Chiu T W. Analytic properties of the vertex function in gauge-theories.I [J].PhysicalReviewD, 1980, 22(10): 2542-2549. [25]Haymaker R W. Variational-methods for composite-operators[J].RivistadelNuovoCimento,1991, 14(8):1-89. [26]Burden C J, Roberts C D. Gauge covariance and the fermion-photon vertex in 3-dimensional and 4-dimensional, massless quantum electrodynamics[J].PhysicalReviewD, 1993, 47(12):5581-5588. [27]Stam K. Dynamical chiral symmetry-breaking[J].PhysicsLettersB, 1985, 152(3/4): 238-240. [28]Cornwall J M, Jackiw R, Tomboulis E. Effective action for composite operators[J].PhysicalReviewD, 1974, 10(8):2428-2445. 三维QED中的动力学手征对称破缺 周雨青 (东南大学物理系, 南京 211189) 为了研究非微扰理论中的传播子行为,以及协变规范对其行为的影响,以常用的截断方案下的Dyson-Schwinger方程为基础,采用数值联立求解的方法研究了三维量子电动力学(QED)中的费米子和玻色子的行为,并获得了一系列不同规范下费米传播子在Nambu和Wigner相中的自洽解.对这些数值解的分析表明,远离Landau规范的红外区处,传播子行为明显不同于Landau规范中的行为.基于Nambu和Wigner相中的不同规范下的传播子,进一步对等效压力差和费米凝聚随规范参数的变化做了比较,结果表明,采用CJT等效势描述的相变与手征凝聚描述的手征相变两者之间不完全自洽. 传播子; 协变规范; 三维QED; 等效压力差; 费米凝聚; 手征相变 O572.24;O413.2 Received 2014-06-21. Biography:Zhou Yuqing (1961—), male, doctor,professor,zhou-yuqing@263.net. s:The National Natural Science Foundation of China (No.10947127), the Science Foundation of Southeast University(No.11047005), :Zhou Yuqing.Dynamical chiral symmetry breaking in QED3[J].Journal of Southeast University (English Edition),2014,30(4):544-549. 10.3969/j.issn.1003-7985.2014.04.024 10.3969/j.issn.1003-7985.2014.04.024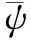
1 Truncated Dyson-Schwinger Equations for Propagators
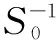
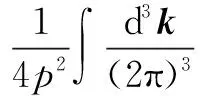
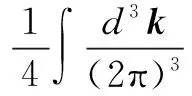
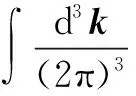
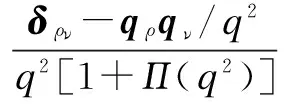
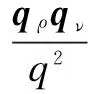
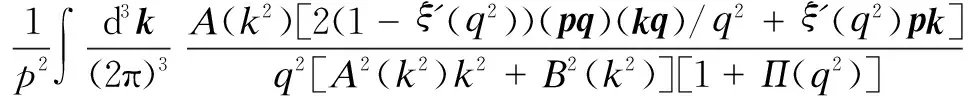
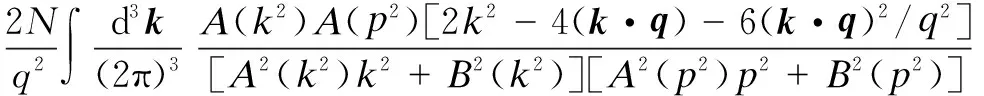

2 Numerical Results



3 Physical Phase

4 Conclusion
猜你喜欢
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Improved design of reconfigurable frequency response masking filters based on second-order cone programming
- Experimental study on thermal characteristicsof a double skin façade building
- Gene expression profile in H4IIE rat hepatoma cells exposed to an antifouling booster biocide Irgarol-1051 degradation product
- Synthesis and application of an environmentallyfriendly antiscalant in industrial cooling systems
- L(1,2)-edge-labeling for necklaces
- Design and implementation of multi-hop video transmission experiment system in VANET
