Improved design of reconfigurable frequency response masking filters based on second-order cone programming
2014-09-06WuChenXuXinzhouHuangChengweiZhaoLi
Wu Chen Xu Xinzhou Huang Chengwei Zhao Li
(1Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Physical Science and Technology, Soochow University, Suzhou 215006, China)
Improved design of reconfigurable frequency response masking filters based on second-order cone programming
Wu Chen1Xu Xinzhou1Huang Chengwei2Zhao Li1
(1Key Laboratory of Underwater Acoustic Signal Processing of Ministry of Education, Southeast University, Nanjing 210096, China)(2School of Physical Science and Technology, Soochow University, Suzhou 215006, China)
In order to improve the design results for the reconfigurable frequency response masking (FRM) filters, an improved design method based on second-order cone programming (SOCP) is proposed. Unlike traditional methods that separately design, the proposed method takes all the desired designing modes into consideration when designing all the subfilters. First, an initial solution is obtained by separately designing the subfilters, and then the initial solution is updated by iteratively solving a SOCP problem. The proposed method is evaluated on a design example, and simulation results demonstrate that jointly designing all the subfilters can obtain significantly lower minimax approximation errors compared to the conventional design method.
frequency response masking (FRM) filter; optimal design; reconfigurability; second-order cone programming (SOCP)
Recently, a new reconfigurable filter bank architecture based on frequency response masking (FRM) technique was proposed[1]. The FRM technique is well known for its low complexity in designing sharp transition-band finite impulse response (FIR) filters[2]. When incorporating reconfigurability into the FRM filters, low complexity and reconfigurability, which are the two key requirements of the filters used for multi-standard communication, can be satisfied. Hence, the reconfigurable FRM filters have been extensively used in software defined radio (SDR) channelization[1,3-4], cognitive radio handsets channel adaptation[5], and cognitive radio spectrum sensing[6].
Previous work on reconfigurable FRM filters mainly focused on its applications and implementations. Their designing procedure generally involves two steps: First, obtaining the specifications of all the subfilters, and secondly, designing all the subfilters with precalculated specifications using the Parks-McClellan algorithm[7]. However, designing all the subfilters separately is an indirect method, which produces suboptimal solutions.
For the optimal design of reconfigurable FRM filters, all the subfilters are expected to be designed directly according to the desired multi-mode. It has been demonstrated that, for the design of reconfigurable coefficient decimation FIR filters, taking all configuration modes into consideration can give better results[8]. However, as the cascade structure of the FRM filters, linear programming (LP) used in Ref.[8] will not be appropriate for the optimal design of reconfigurable FRM filters. In earlier work, the second-order cone programming (SOCP)[9]was employed for the optimal design of a basic single mode FRM filter[10-11]. So, in this paper, we propose an improved design method, which takes all the desired modes into consideration. The optimal design of reconfigurable FRM filters can be formulated as the SOCP problem. Given a reasonable initial design solution, an improved design can be obtained by iteratively solving the SOCP problem.
1 Review of Reconfigurable FRM Filters
1.1 Basic FRM filter
FRM filters have been widely used for the synthesis of sharp transition-band filters with low complexity. The basic FRM filter structure is illustrated in Fig.1, which includes a modal filterHa(z) upsampled byM, a pair of masking filtersHma(z) andHmc(z), and a delay line[2]. Since the desired sharp transition-band filter is composed of several wide transition-band subfilters, the overall complexity can be reduced. The transfer function of the entire basic FRM filter is given by
H(z)=Ha(zM)Hma(z)+[z-0.5M(Na-1)-Ha(zM)]Hmc(z)
(1)
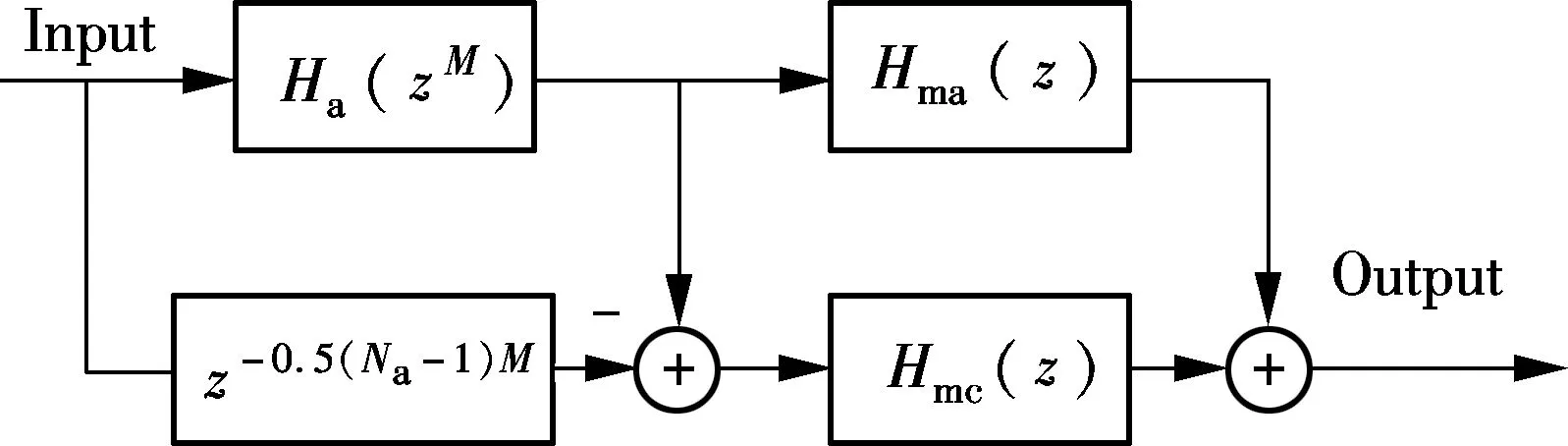
Fig.1 Basic FRM filter structure
where
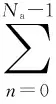
(2)
If the length of the two masking filters are both even or both odd and (Na-1)Mis even, the FRM filter will have a linear phase response. Without loss of generality, the FRM filter can be treated as a zero-phase FIR filter, which can be expressed as
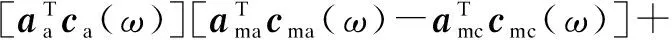
(3)
where
Given a up-sampling factorM, normalized passband edgeωpand stopband edgeωsof the desired filter, the passband and stopband edges of all the subfilters can be determined as follows[1-3]:

m=
(4a)
ωap=ωpM-2mπ,ωas=ωsM-2mπ
(4b)

(4c)
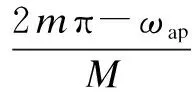
(4d)
wheremdenotes the largest integer less thanωpM/(2π);ωapandωasare the passband and stopband edges of the modal filterHa(z);ωmapandωmcpare the passband edges andωmasandωmcsare the stopband edges of the two masking filtersHma(z) andHmc(z), respectively.
The length of each of the subfilter can be obtained by
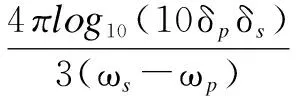
(5)
whereδpis the peak passband ripple;δsis the peak stopband ripple andωs-ωpis the normalized transition width[12].
1.2 Reconfigurable FRM filter
For reconfigurable FRM filters, reconfigurability is achieved by reusing the same coefficients of the modal filter with different up-sampling factors. When combining the FRM structure with reconfigurable architecture, low complexity and reconfigurability requirements can be satisfied simultaneously. Generally, there are two architectures of reconfigurable FRM filters, which are shown in Fig.2. The architecture shown in Fig.2(a) can realize a single filter at a given time with the model selector, which is mainly used in SDR handset applications[1,5]. Multiple output architecture is shown in Fig.2(b), which can simultaneously realize multiple channel filters for multimode communication applications[2,4,6]. However, the coefficients of all subfilters of the two architectures are calculated in the same way. The proposed method can be used for the design of both reconfigurable FRM filters.

(a)
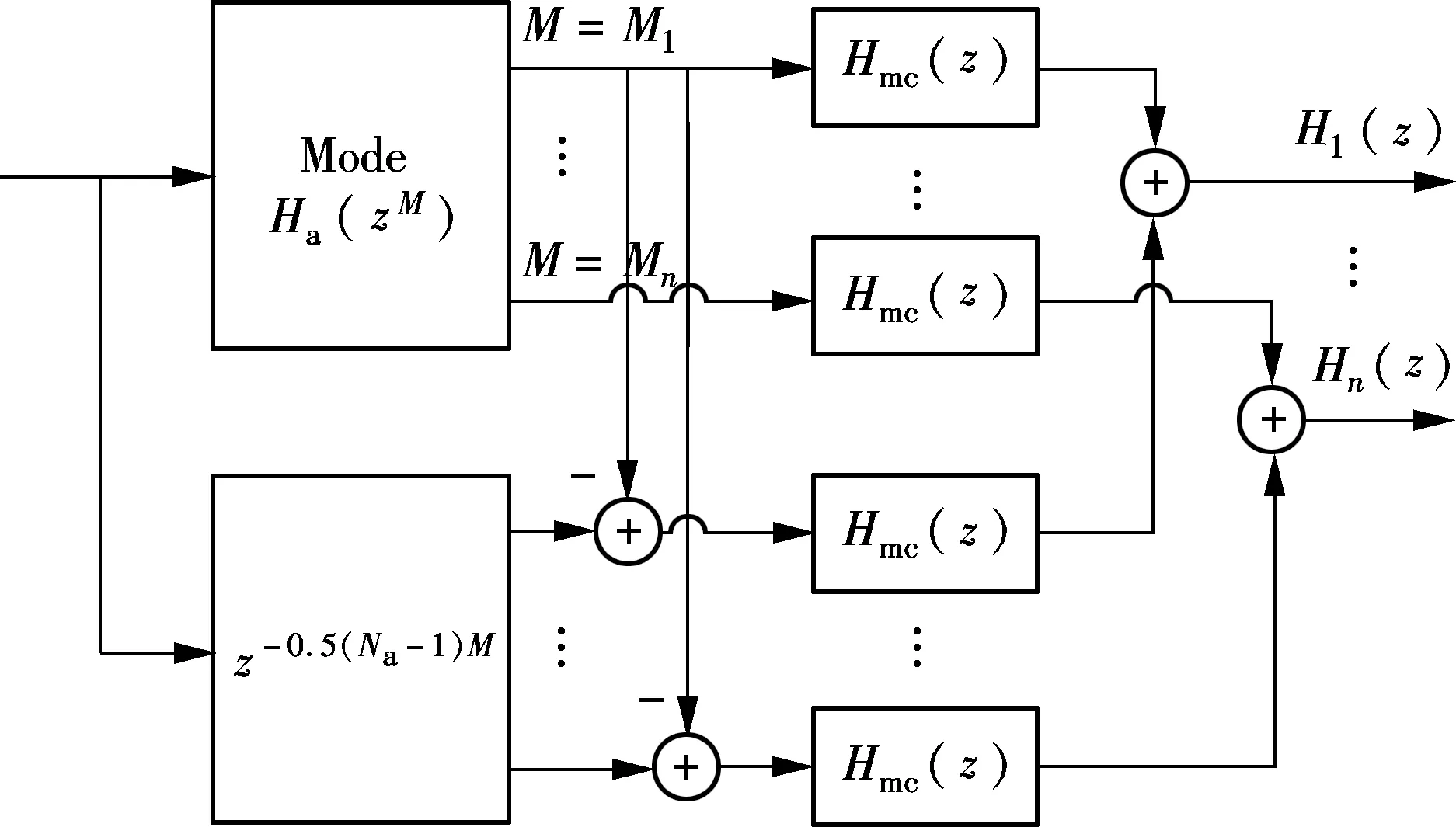
(b)
For reconfigurable FRM filters, the passband edgeωapand the stopband edgeωasof the modal filterHa(z) remain unchanged. Suppose that there arendesired output modes with passband edgesωp1,…,ωpnand stopband edgesωs1,…,ωsn, respectively. Then all the desired output modes can be achieved by using different up-sampling factorsMi, which can be obtained by
ωap=ωp1M1-2π
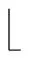
=…=ωpnMn-2π
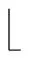
(6a)
ωas=ωs1M1-2π
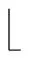
=…=ωsnMn-2π
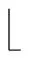
(6b)
After obtaining the different up-sampling factorsMiby sloving Eqs.(6), the complementary delays of different output modes can be obtained by (Na-1)Mi/2, and the passband and stopband edges of the two masking filters for different modes can be obtained using Eqs.(4c) and (4d). Then the length of all the subfilters can be calculated via Eq.(5). As all the subfilters involved in the reconfigurable FRM filters have a wide transition-band, the overall filter lengths can be short and consequently, the complexity can be reduced. Finally, the subfilters are designed using the conventional Parks-McClellan algorithm[7]after all their specifications have been obtained from previous work.
2 Proposed Method
Although previous designing methods can provide acceptable results in multi-mode communication applications[1-2,4-6], designing all the subfilters separately is an indirect method, which leads to the solutions being suboptimal[10]. We therefore consider improving the design results by directly taking all the desired output modes into account. This basic idea is motivated by Ref.[8] that taking all the desired modes into consideration can provide better results for the design of reconfigurable coefficient decimation FIR filters. However, due to the cascade structure of the FRM filters, the linear programming (LP) used in Ref.[8] will not be appropriate for the optimal design of reconfigurable FRM filters. Alternatively, we formulate the optimal design of reconfigurable FRM filters as a SOCP problem. Given a reasonable initial design solution, an improved design can be obtained by iteratively solving the SOCP problem.
The problem of optimal designing of reconfigurable FRM filters taking all desired output modes into consideration with the weighted minimax error criterion can be formulated as follows:
minη
(7a)
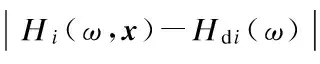
(7b)
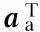
(8)
andWi(ω) is the weighting function defined as
(9)
For solving the problem (7), we use an iterative method with each iteration carried out by a SOCP solver. Suppose that there is a reasonable solutionx0to start, and we are now in thek-th iteration. For a smoothHi(ω,x) in a vicinity ofxk, we can write
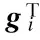
(10)
wheregi(ω,xk) is the gradient ofHi(ω,x)with respect toxafter evaluating atxkand it is defined as
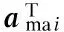
(11)
Hence, provided the ‖δ‖ is small and the filter is in linear phase, withx=xk+δwe obtain
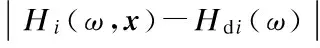
(12)
wheregik(ω)=Wi(ω)gi(ω,xk) andeik(ω)=Wi(ω)·[Hi(ω,xk)-Hdi(ω)].
From (10) and (12), it follows that an approximation solution of (7) in thek-th iteration can be obtained by solving the following SOCP problem:
mincTμ
(13a)
s.t. ‖Gik(ω)μ+eik(ω)‖≤cTμω∈Ωi,∀i
(13b)
‖Bμ‖≤b
(13c)


The general procedure of the proposed design method is listed as follows:
1) Choose an appropriate mode filter with specifications ofωapandωas.
2) Solve Eq.(6) to obtain the up-sampling factorMiof thei-th desired mode, and then obtain the specifications of each pair of masking filters using Eq.(4).
3) Obtain the length of all the subfilters using Eq.(5).
4) Design all the subfilters with precalculated specifications using the Parks-McClellan algorithm[7]for the initial solutionx0,k=0.

3 Design Example
The design example selected for this paper was adopted from Ref.[1], which is used for the SDR channelizer. The specifications of the modal filter areωap=0.4π,ωas=0.5π andNa=39. The specifications of all masking filters and the desired filters are shown in Tab.1. The weighting factors are selected as unity weights in both the passband and stopband. For each mode, 512 points in total are uniformly placed in the desired frequency bands of interest. The value of boundbin constraint (13c) should be proportional to the dimension of vectorx[10]. In this paper, we setbto be 0.5 and the tolerance value to be 0.000 5. We use the SeDuMi toolbox[13]to solve the SOCP problem (13).
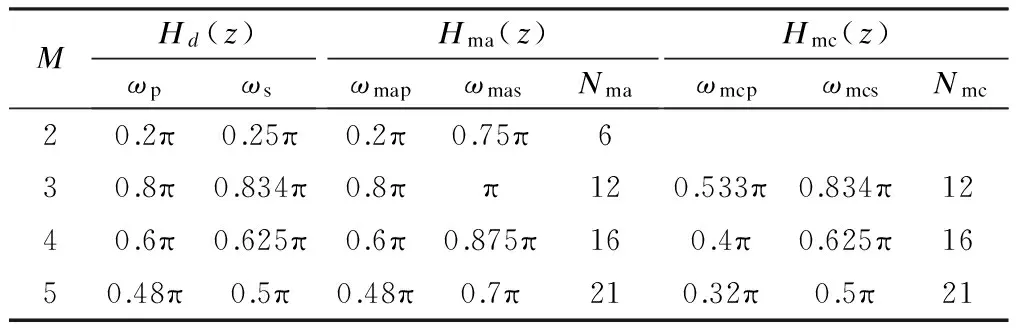
Tab.1 Specifications of subfilters and the desired filters
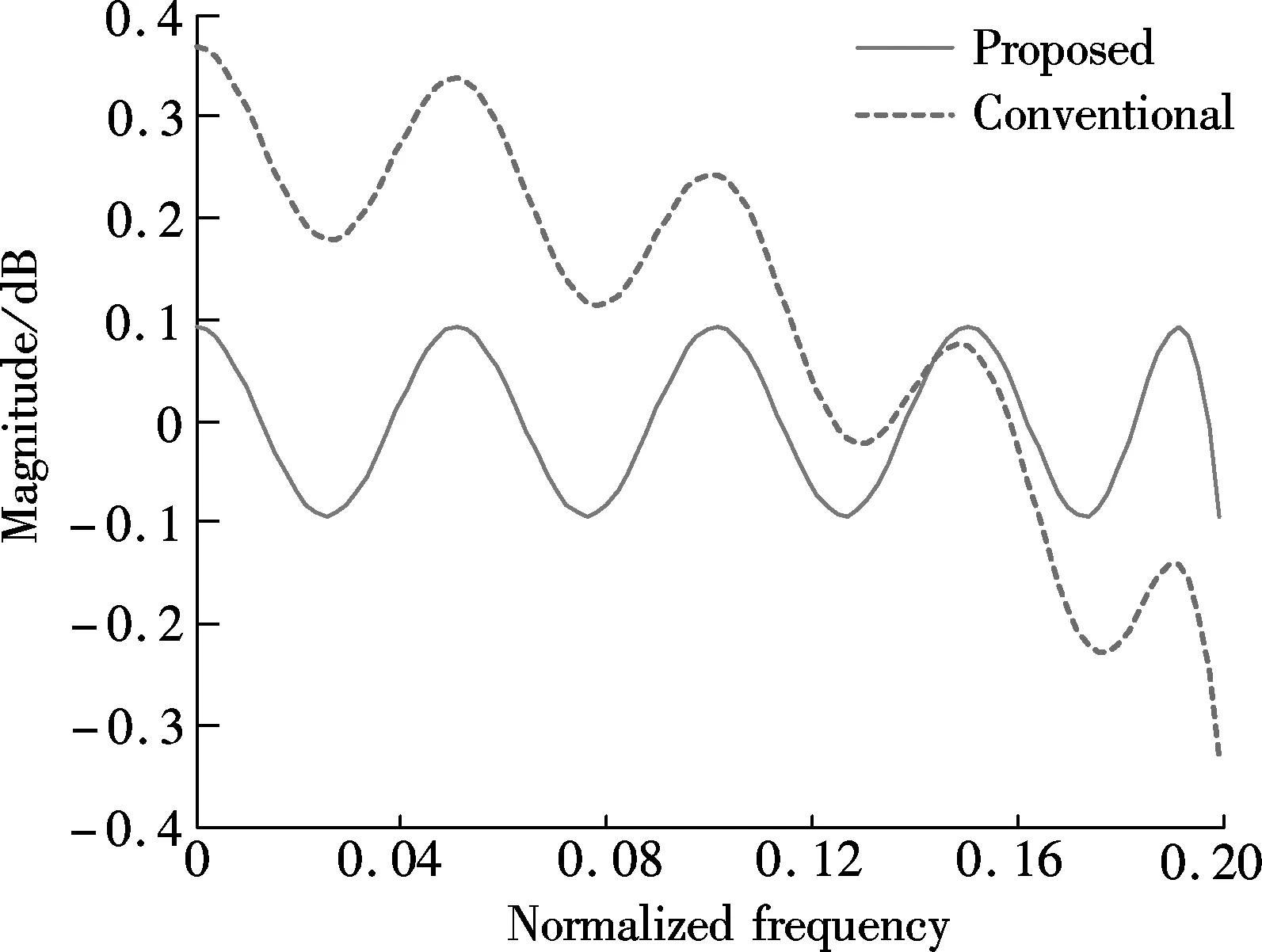
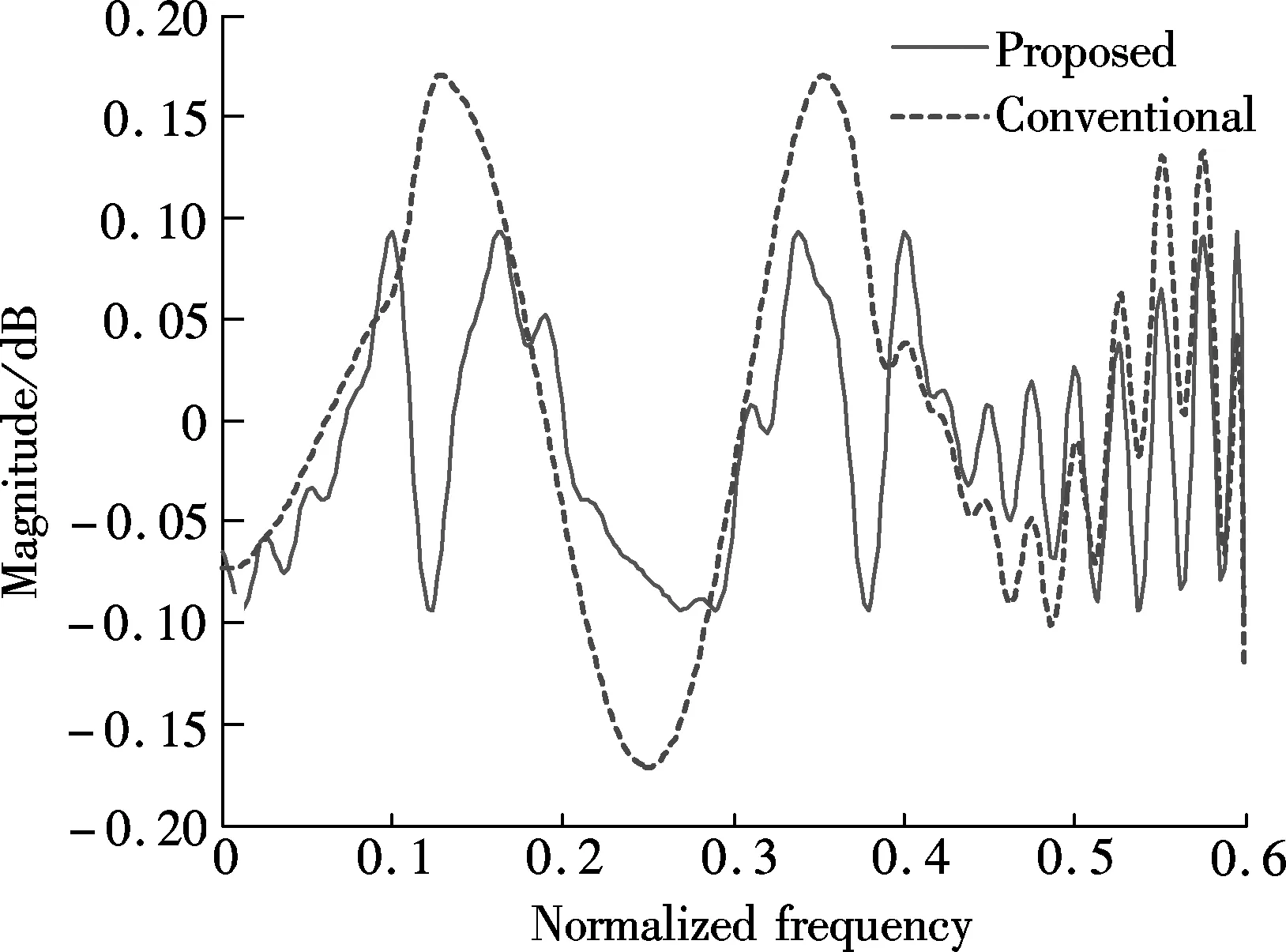
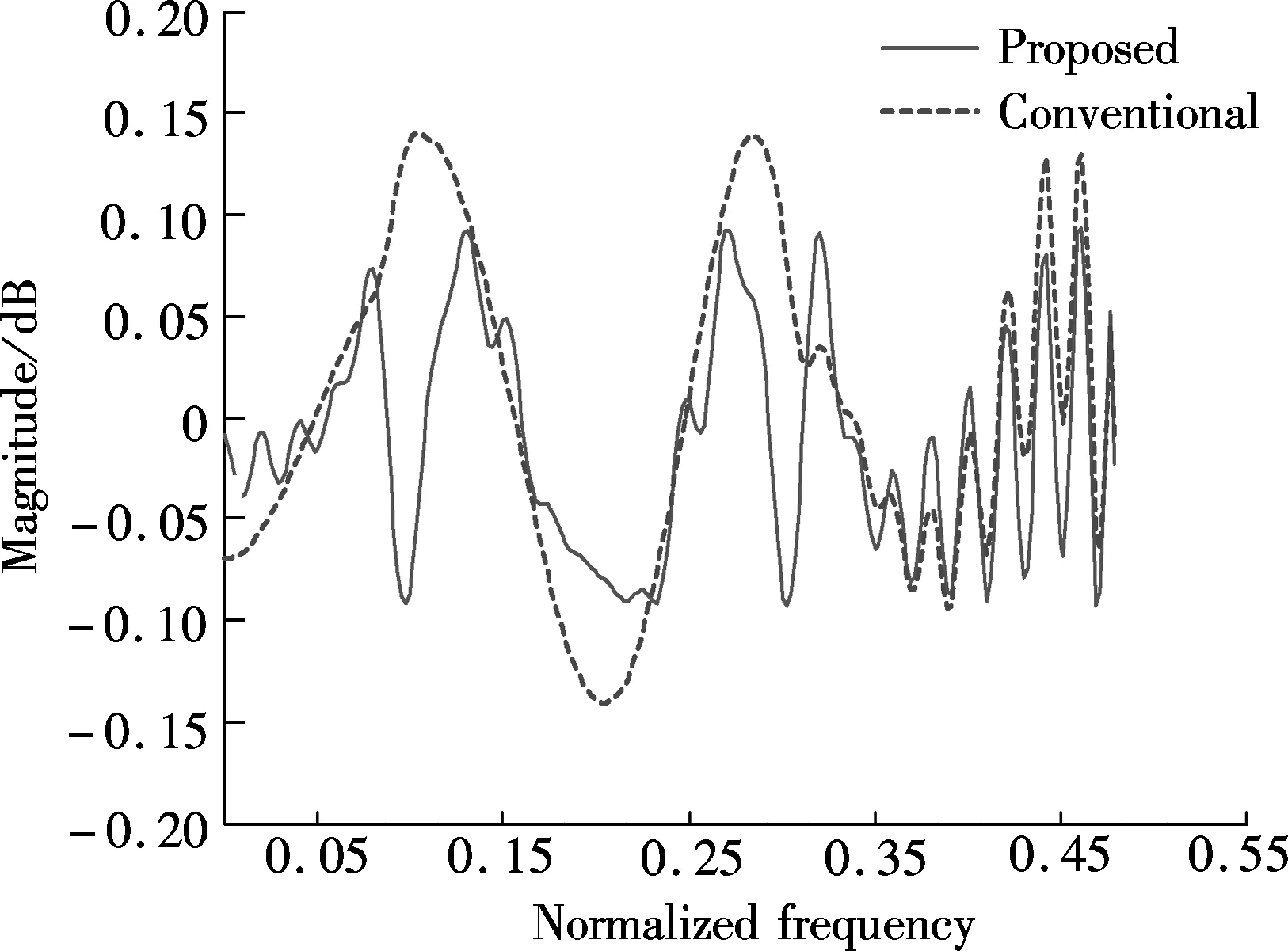
The magnitude responses and the passband ripples of both the proposed design method as well as the conventional method used in previous work are shown in Fig.3 and Fig.4, respectively. As can be clearly seen, the proposed method can produce filters with lower minimax approximation errors. The maximum passband ripples and the minimum stopband attenuation of the two design methods for each mode are shown in Tab.2. It is observed that the proposed method significantly outperforms the previous design method. Hence, as can be expected, the proposed method can give improved performance in multi-mode communication applications.
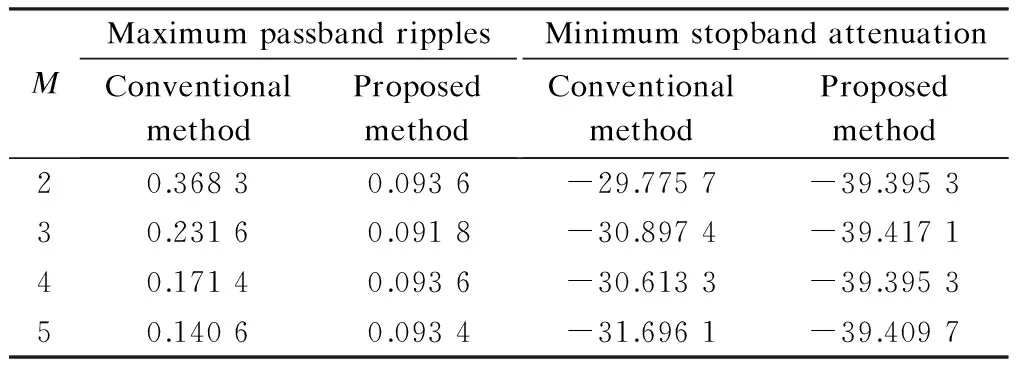
Tab.2 Maximum passband ripples and minimum stopband attenuation dB
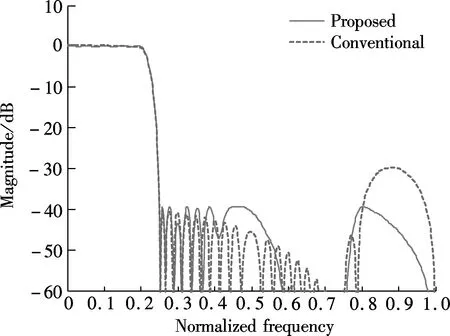
(a)
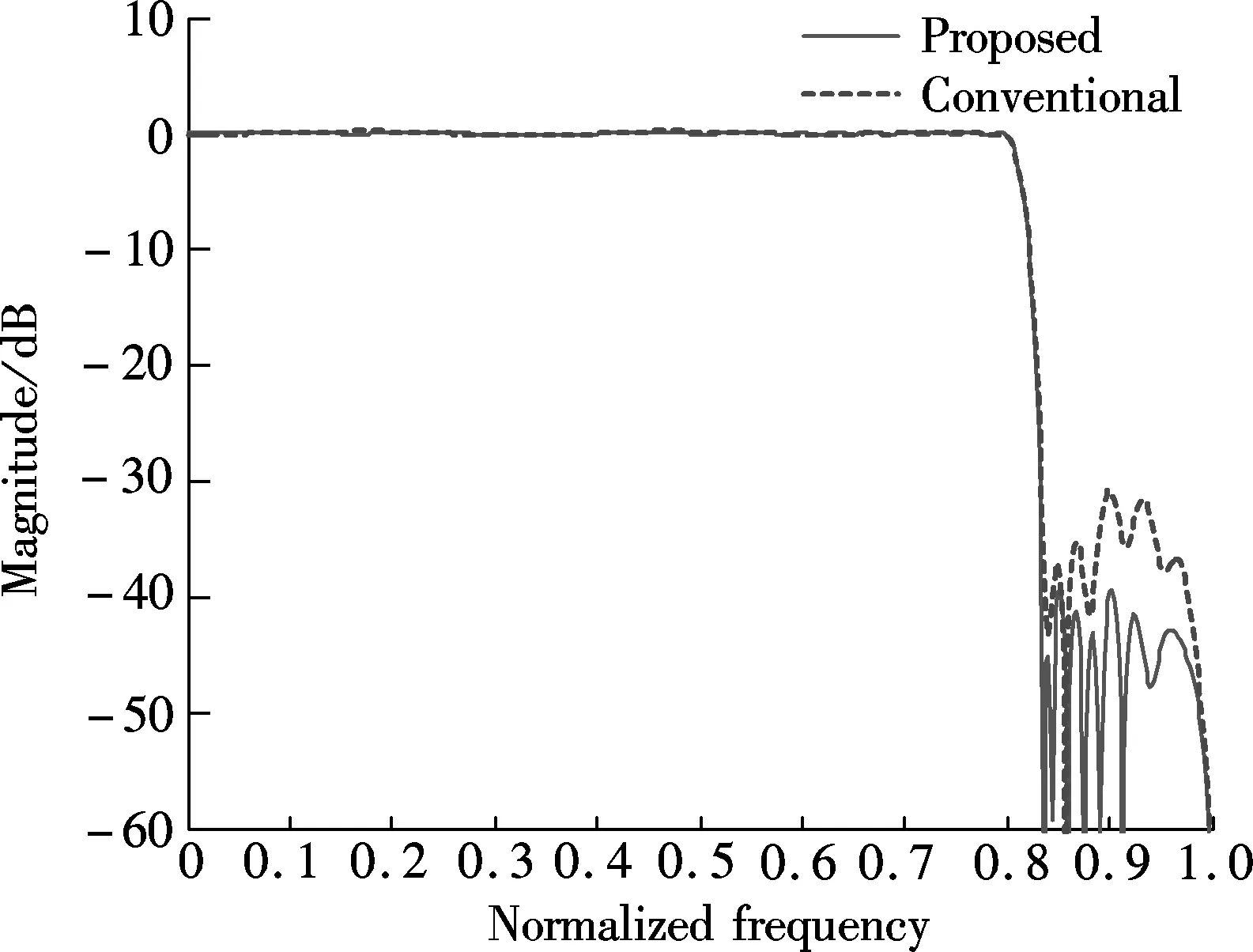
(b)

(c)
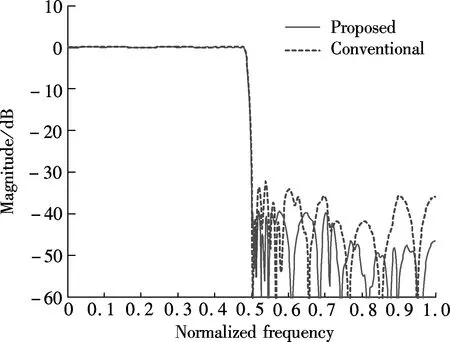
(d)
(a)

(b)
(c)
(d)
4 Conclusion
An optimal approach for the design of reconfigurable frequency response filters is proposed, which takes all desired designing modes into consideration. The proposed method mainly involves two steps: first an initial solution by separately designing the subfilters is obtained from previous work, and then the initial solutions are improved by iteratively solving a second-order cone programming (SOCP) problem. The simulation results demonstrate that the proposed method can obtain significantly lower minimax approximation errors compared to the conventional design method. The proposed method is expected to improve the performance of reconfigurable FRM filters in multi-mode communication applications.
[1]Mahesh R, Vinod A P. Reconfigurable frequency response masking filters for software radio channelization [J].IEEETransactionsonCircuitsandSystemsⅡ:ExpressBriefs, 2008, 55(3): 274-278.
[2]Lim Y C. Frequency-response masking approach for the synthesis of sharp linear phase digital filters [J].IEEETransactionsonCircuitsandSystems, 1986, 33(4): 357-364.
[3]Mahesh R, Vinod A P. Reconfigurable low area complexity filter bank architecture based on frequency response masking for nonuniform channelization in software radio receivers [J].IEEETransactionsonAerospaceandElectronicSystems, 2011, 47(2): 1241-1255.
[4]Mahesh R, Vinod A P, Lai E M-K, et al. Filter bank channelizer for multi-standard software defined radio receivers [J].JournalofSignalProcessingSystems, 2011, 62(2): 157-171.
[5]Smitha K G, Vinod A P. A new low power reconfigurable decimation-interpolation and masking based filter architecture for channel adaptation in cognitive radio handsets [J].PhysicalCommunication, 2009, 2(1/2): 47-57.
[6]Mahesh R, Vinod A P, Moy C, et al. J. A low complexity reconfigurable filter bank architecture for spectrum sensing in cognitive radios[C]//Proceedingsofthe3rdInternationalConferenceonCognitiveRadioOrientedWirelessNetworksandCommunications. Singapore, 2008: 4562506-1-4562506-6.
[7]Parks T, McClellan J. Chebyshev approximation for nonrecursive digital filters with linear phase [J].IEEETransactionsonCircuitTheory, 1972, 19(2): 189-194.
[8]Sheikh Z U, Gustafsson O. Linear programming design of coefficient decimation FIR filters [J].IEEETransactionsonCircuitsandSystemsⅡ:ExpressBriefs, 2012, 59(1): 60-64.
[9]Boyd S, Vandenberghe L.Convexoptimization[M]. Cambridge, UK: Cambridge University Press, 2009.
[10]Lu W S, Hinamoto T. Optimal design of FIR frequency-response-masking filters using second-order cone programming [C]//Proceedingsofthe2003InternationalSymposiumonCircuits,andSystems. Bangkok, Thailand, 2003: 878-881.
[11]Lu W S, Hinamoto T. Optimal design of IIR frequency-response-masking filters using second-order cone programming [J].IEEETransactionsonCircuitsandSystemsⅠ:FundamentalTheoryandApplications, 2003, 50(11): 1401-1412.
[12]Bellanger M G. On computational complexity in digital filters [C]//ProceedingsoftheEuropeanConferenceonCircuitTheoryandDesign. Hague, Holland, 1981: 8-63.
[13]Sturm J F. Using SeDuMi 1.02, a Matlab toolbox for optimization over symmetric cones [J].OptimizationMethodsandSoftware, 1999, 11(1/2/3/4): 625-653.
基于二阶锥优化的改进可重构频罩滤波器设计
吴 尘1徐新洲1黄程韦2赵 力1
(1东南大学水声信号处理教育部重点实验室,南京210096)(2苏州大学物理科学与技术学院,苏州215006)
为了提高可重构频罩滤波器的设计结果,提出了一种基于二阶锥优化的改进设计方法.不同于传统的将所有子滤波器分开设计的方法,该方法将所有期望的设计模式纳入到设计目标中来联合设计所有子滤波器.首先,单独设计所有子滤波器以获得一个初始结果;然后,迭代求解一个二阶锥优化问题,以更新初始结果.通过一个设计实例来验证所提出算法的有效性.仿真结果表明,相比于传统的设计方法,将所有子滤波器联合设计能够显著降低minimax准则的设计误差.
频罩滤波器;最优设计;可重构;二阶锥优化
TN911.72
Received 2014-02-28.
Biographies:Wu Chen(1987—),male,graduate; Zhao Li(corresponding author), male, doctor, professor, zhaoli@seu.edu.cn.
s:The National Natural Science Foundation of China (No.61231002, 61273266, 61375028), the Ph.D. Programs Foundation of Ministry of Education of China (No.20110092130004).
:Wu Chen, Xu Xinzhou, Huang Chengwei, et al.Improved design of reconfigurable frequency response masking filters based on second-order cone programming[J].Journal of Southeast University (English Edition),2014,30(4):422-427.
10.3969/j.issn.1003-7985.2014.04.004
10.3969/j.issn.1003-7985.2014.04.004
猜你喜欢
杂志排行
Journal of Southeast University(English Edition)的其它文章
- Experimental study on thermal characteristicsof a double skin façade building
- Gene expression profile in H4IIE rat hepatoma cells exposed to an antifouling booster biocide Irgarol-1051 degradation product
- Synthesis and application of an environmentallyfriendly antiscalant in industrial cooling systems
- L(1,2)-edge-labeling for necklaces
- Design and implementation of multi-hop video transmission experiment system in VANET
- Measurement of spatiotemporal characteristics of femtosecond laser pulses by a modified single-shot autocorrelation
