L(1,2)-edge-labeling for necklaces

He Dan Lin Wensong

(Department of Mathematics, Southeast University, Nanjing 211189, China)



L(1,2)-edge-labeling for necklaces

He Dan Lin Wensong

(Department of Mathematics, Southeast University, Nanjing 211189, China)

channel assignment;L(j,k)-edge-labeling; Cartesian product; Halin graph; necklace

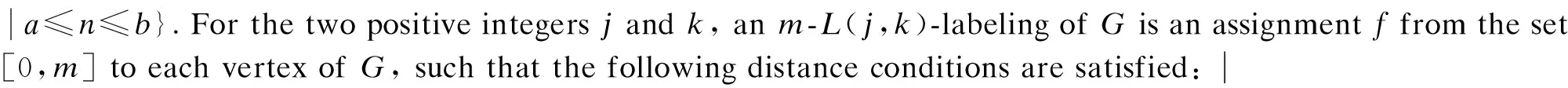
TheL(j,k)-labeling of graphs is inspired by the channel assignment problem introduced by Hale[2]. TheL(2,1)-labeling was formulated and studied by Griggs and Yeh[3]in 1992. Since then,L(2,1)-labeling andL(j,k)-labeling (j≥k) of graphs have been studied extensively. Refer to surveys[4-5].

A variation of the channel assignment problem is the code assignment in computer networks[6]. The task is to assign integer “control codes” to a network of computer stations with distance restrictions. This is the same as the problem ofL(j,k)-labeling withj≤k. Jin and Yeh[6]studied theL(j,k)-labeling for (j,k)∈{(0,1),(1,1),(1,2)}. Calamoneri et al.[7]investigated theλj,k-numbers of trees withj≤k. Chen et al.[8-10]also studied theL(j,k)-labeling forj≤k.

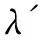
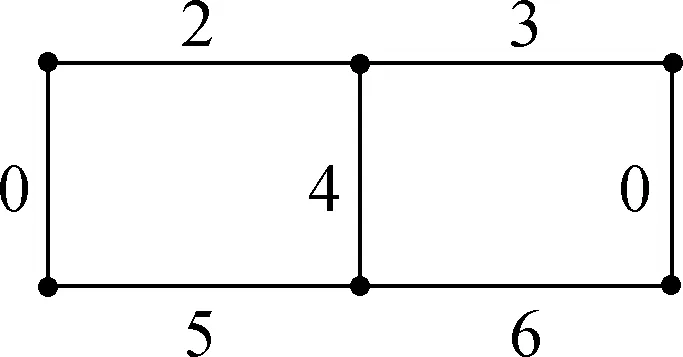
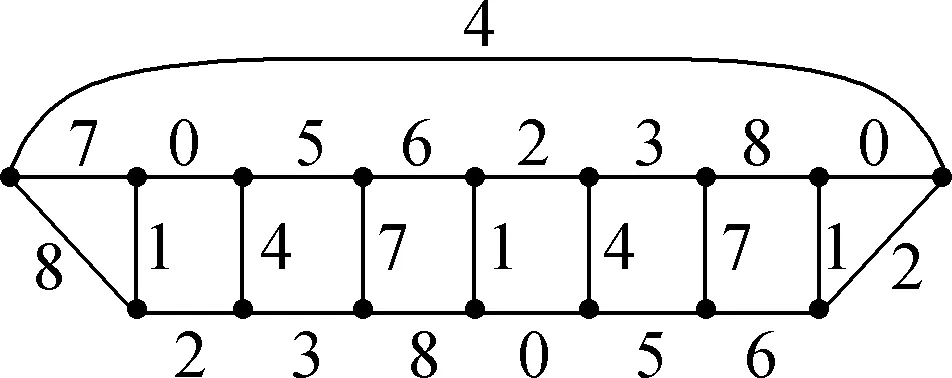
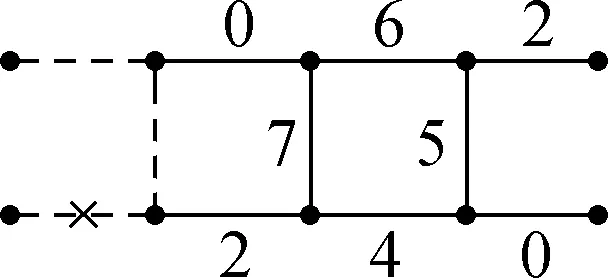
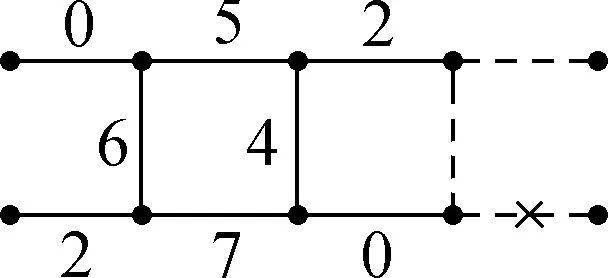
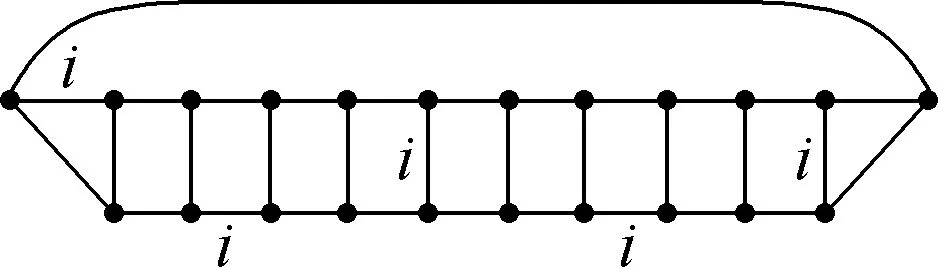
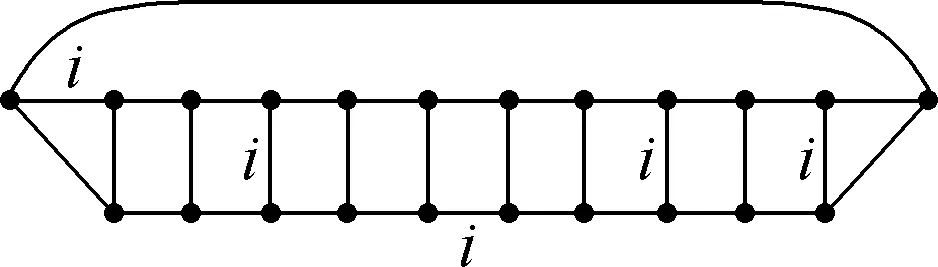
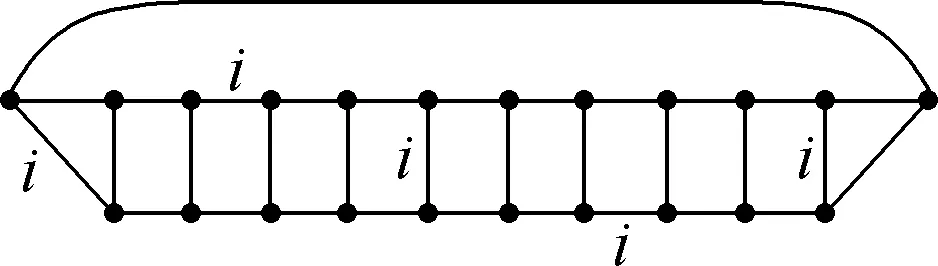
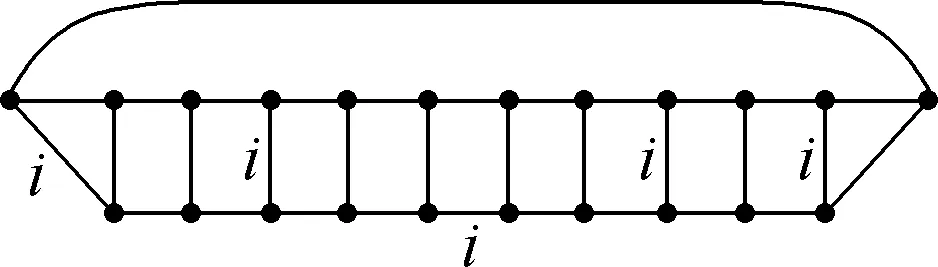
Suppose thatTis a tree with no vertex of degree two and at least one vertex of degree three or more. A Halin graphG=T∪Cis a planar graph, whereCis a cycle connecting the leaves (vertices of degree 1) ofTin the cyclic order determined by a drawing ofT. A caterpillar is a tree such that after the removal of the leaves it becomes a path. Forh≥1, suppose thatThis a caterpillar with the pathPh+2of lengthh+1. The vertices alongPh+2are marked with 0,1,…,h,h+1, and the other vertices are marked with 1′,2′…,h′ such that {i,i′}∈E(Th) (1≤i≤h). The necklaceNehis a graph obtained fromThby adding the edges {0,1′},{1′,2′},…,{h′,h+1} and {h+1,0} (see Fig.1). Note that necklaces form a specific class of 3-regular Halin graph andNe1≅K4.

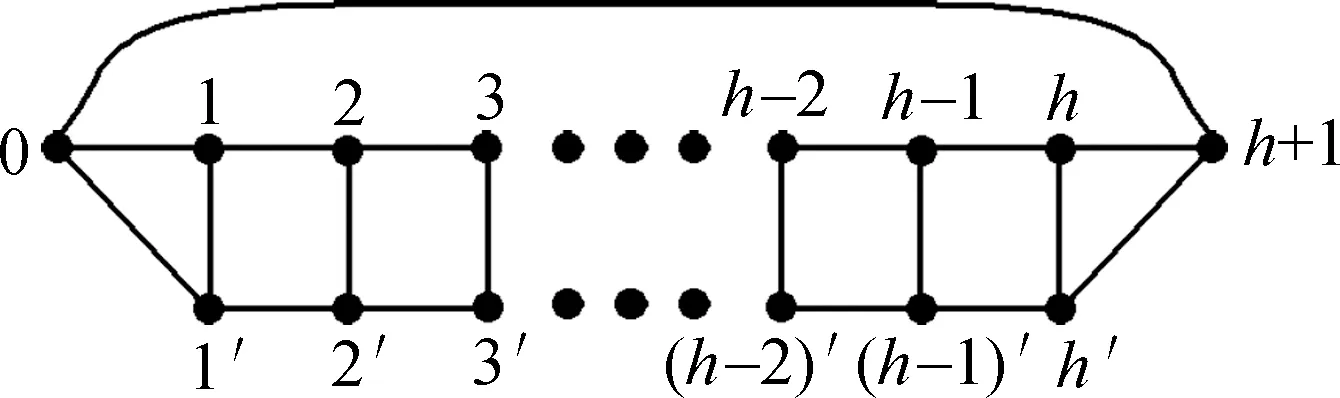
Fig.1 Necklace Neh

1 Cartesian Produce of P2and Ph

Theorem 1 LetPhbe a path withh≥2 vertices. Then

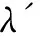
(a) (b)

Fig.3 A periodic 7-L(1,2)-edge-labeling of P2□P18

2 Necklaces

Theorem 2 LetNehbe a necklace. Then

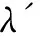
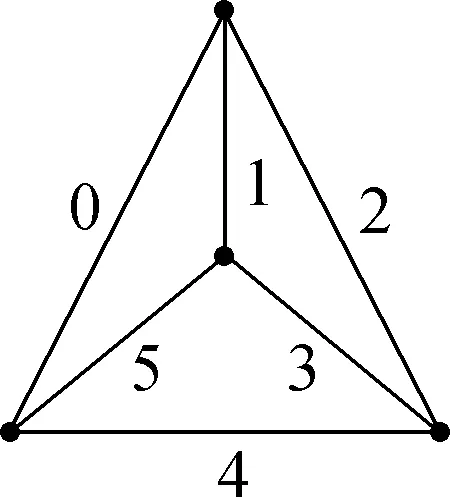
Fig.4 A 5-L(1,2)-edge-labeling of Ne1

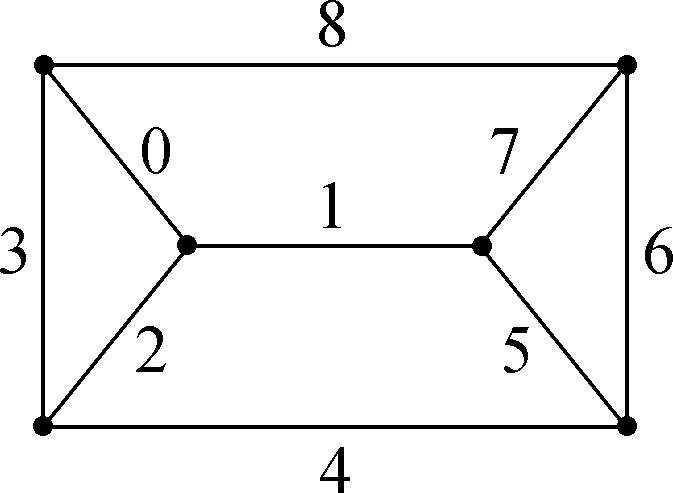
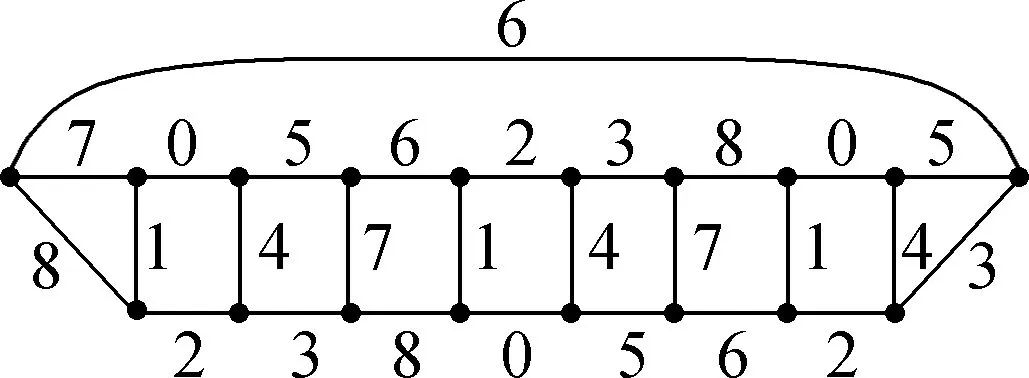
Fig.5 An 8-L(1,2)-edge-labeling of Ne2

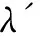
Fig.6 An 8-L(1,2)-edge-labeling of Ne3

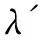
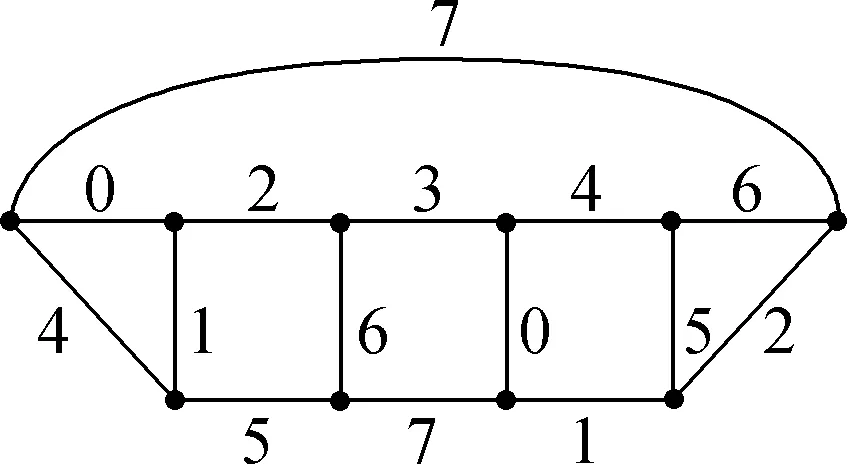
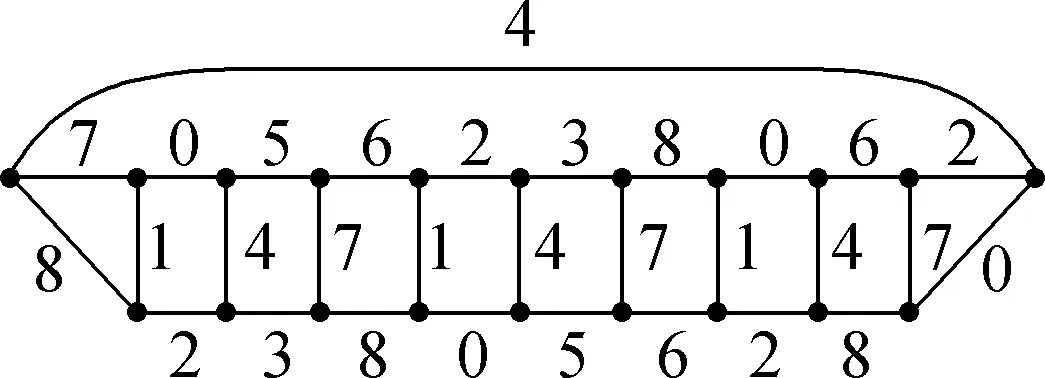
Fig.7 A 7-L(1,2)-edge-labeling of Ne4

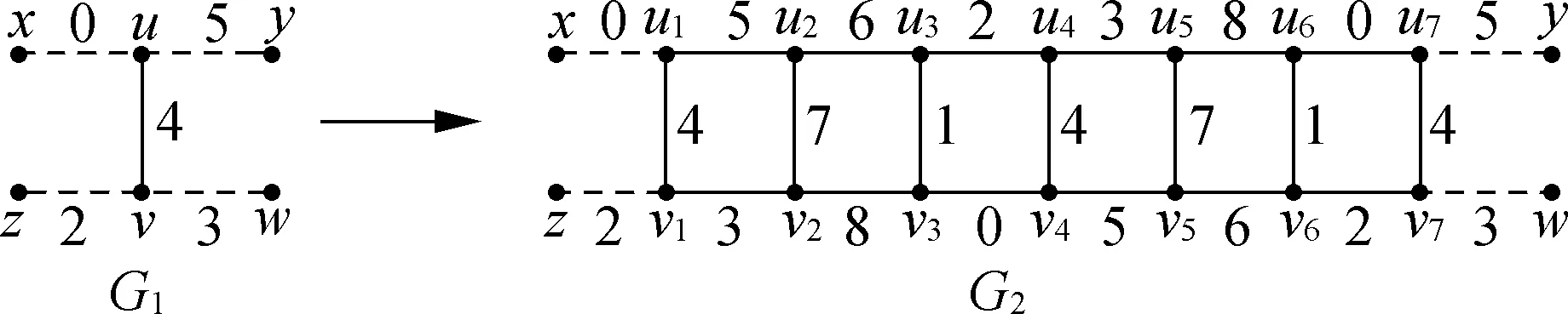
Fig.8 The extension of 8-L(1,2)-edge-labeling of G1

Proof Fig.8 shows the extension offto a 8-L(1,2)-edge labeling ofG2.

(a) (b)

(c) (d)

(e)

(f)

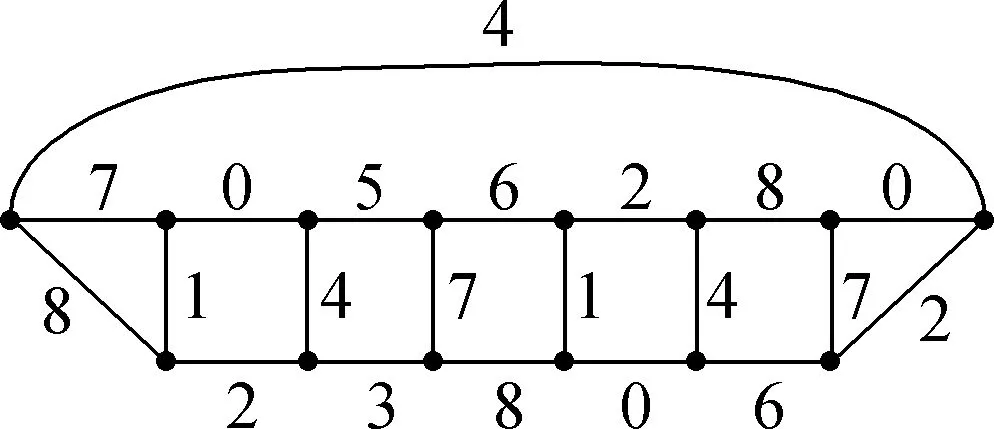
Fig.10 The extension of 7-L(1,2)-edge-labeling of Ne4given in Fig.7

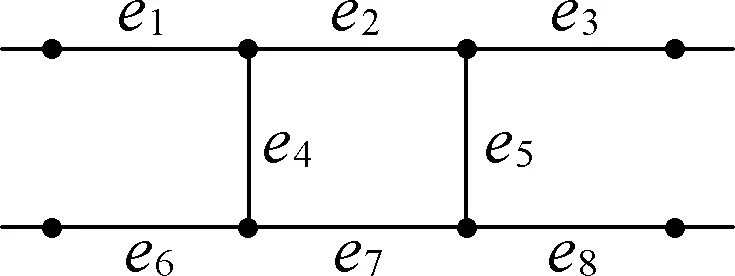
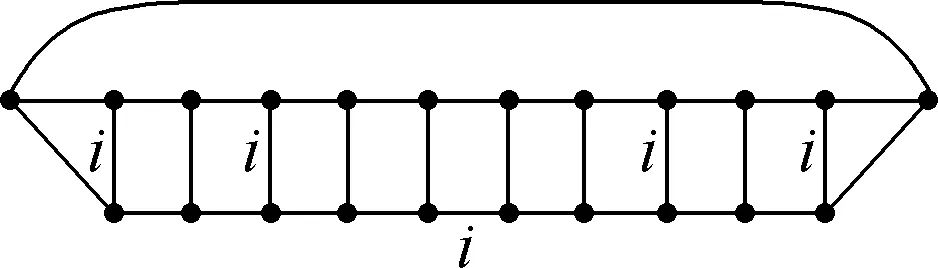
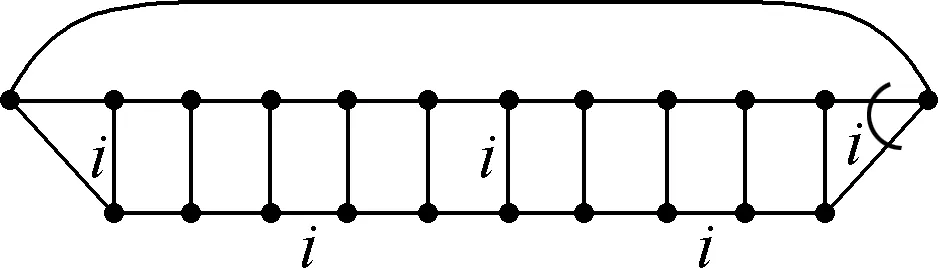
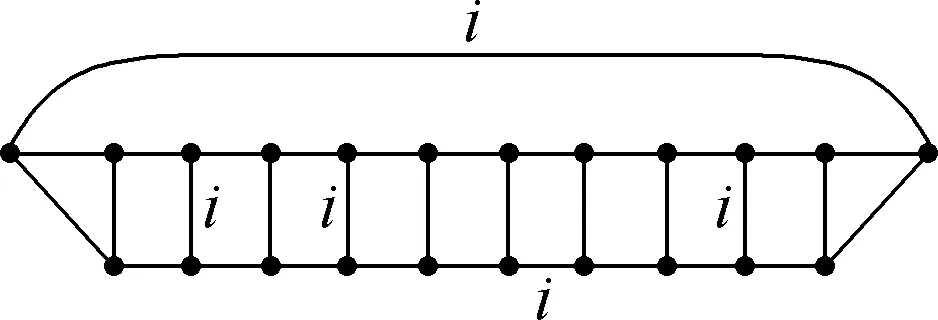
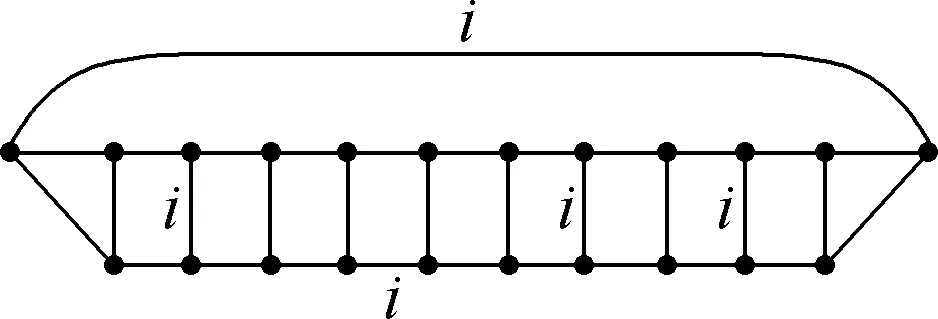
Fig.11 Locations of the edges in i

Claim 1f(e1)=f(e8) if and only iff(e3)=f(e6).

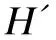
Claim 2 Iff(e1)=f(e8)=aandf(e3)=f(e6)=b, then {a,b}∩{0,7}≠∅.

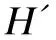
Without loss of generality, we can assume thata=0. Then by Claim 1, Claim 2 and the symmetry of labels, we only need to consider the following three cases:

Case 1a=0 andb∈[3,6].

Case 2a=0 andb=2.

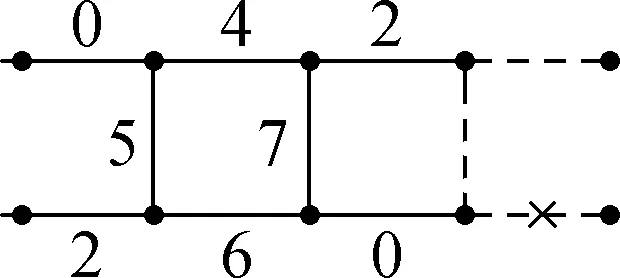
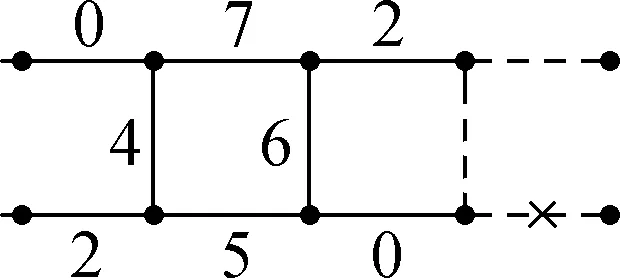
Proof In this case, it is clear that {f(e2),f(e4),f(e5),f(e7)}={4,5,6,7}. Note thate2,e5,e7ande4form a 4-cycle. Due to the distance condition, the four labels 4,5,6 and 7 must be assigned to the above four edges in clockwise or counterclockwise order along the cycle. By symmetry, we consider the four cases off(e2)=4,f(e4)=4,f(e7)=4 andf(e5)=4, respectively. For each case, we can obtain a contradiction as indicated in Fig.12 (In the figures, the edges marked with a ford cannot be assigned by the labels in [0,7]).

(a)

(b)

(c)

(d)

Case 3a=0 andb=7.

Proof The proof of this case is similar to the argument of case 2.

By the above arguments, Property 1 holds.

Property 2 For 3≤i≤h-3, the labels assigned to the edges of (i,i′) and (i+2,(i+2)′) must be distinct.

By the symmetry of labels, we can assume thatk=0,1,2 and 3. Whenk=0, without loss of generality, letf(hi-1)=f(h(i+2)′)=1. Then we only need to consider the cases off(h(i-1)′)=f(hi+2)=4,5,6 and 7. For each case, we can obtain a similar contradiction as the proofs in case 2 of Property 1. The situation whenk=1,2 and 3 are similar. Thus, Property 2 holds.

By the above two properties, we obtain the following result.

(a)

(b)

(c)

(d)

(e)

(f)

(g)

(h)

By Properties 1 and 2, this paper is completed by raising the following conjecture:

[1]Bondy J A, Murty U S R.Graphtheory[M]. London: Springer, 2008.[2]Hale W K. Frequency assignment: theory and applications [J].ProceedingsoftheIEEE, 1980,68(12):1497-1514.

[3]Griggs J R, Yeh R K. Labelling graphs with a condition at distance 2 [J].SIAMJournalonDiscreteMathematics, 1992, 5(4):586-595.

[4]Calamoneri T. TheL(h,k)-labelling problem: an updated survey and annotated bibliography [J].TheComputerJournal, 2011,54(8):1344-1371.

[5]Yeh R K. A survey on labeling graphs with a condition at distance two [J].DiscreteMathematics, 2006,306(12):1217-1231.

[6]Jin X T, Yeh R K. Graph distance-dependent labeling related to code assignment in computer networks [J].NavalResearchLogistics, 2005,52(2):159-164.

[7]Calamoneri T, Pelc A, Petreschi R. Labeling trees with a condition at distance two [J].DiscreteMathematics, 2006, 306(14):1534-1539.

[8]Chen Q, Lin W.L(j,k)-labelings andL(j,k)-edge-labelings of graphs [J].ArsCombinatoria, 2012,106:161-172.

[9]Griggs J R, Jin X T. Recent progress in mathematics and engineering on optimal graph labellings with distance conditions [J].JournalofCombinatorialOptimization, 2007,14(2/3):249-257.

[10]Niu Q J. TheL(s,t)-labeling numbers and edge spans of graph [D]. Nanjing: Department of Mathematics, Southeast University, 2007.(in Chinese)

[11]Georges J P, Mauro D W. Edge labelings with a condition at distance two [J].ArsCombinatoria, 2004,70:109-128.

[12]Chen Q. TheL(2,1)-edge-labeling of graphs [D]. Nanjing: Department of Mathematics, Southeast University, 2006. (in Chinese)

[13]Lin W, Wu J. Distance two edge labelings of lattices [J].JournalofCombinatorialOptimization, 2013, 25(4):661-679.

[14]Chang G J, Liu D F. Strong edge-coloring for cubic Halin graphs [J].DiscreteMathematics, 2012,312(8):1468-1475.

[15]Tam W K. The strong chromatic index of cubic Halin graph [D]. Hong Kong: Department of Mathematics, Hong Kong Baptist University, 2003.

项链的L(1,2)-边标号

贺 丹 林文松

(东南大学数学系,南京211189)

频道分配;L(j,k)-边标号;笛卡尔乘积;Halin图;项链

O157.5

Received 2013-04-08．

Biographies：He Dan(1977—),female,graduate; Lin Wensong(corresponding author), male, doctor, professor, wslin@seu.edu.cn.

The National Natural Science Foundation of China (No.10971025, 10901035).

：He Dan, Lin Wensong．L(1,2)-edge-labeling for necklaces[J]．Journal of Southeast University (English Edition),2014,30(4):550-554．

10.3969/j.issn.1003-7985.2014.04.025

10.3969/j.issn.1003-7985.2014.04.025