High-performance channel estimation and compensation scheme for OFDM receivers with IQ imbalances

Shu Feng Tong Juanjuan Li Jun Wang Jin Gu Chen Lu Jinhui

(1School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)(2National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)(3Ministerial Key Laboratory of JGMT, Nanjing University of Science and Technology, Nanjing 210094, China)



High-performance channel estimation and compensation scheme for OFDM receivers with IQ imbalances

Shu Feng1,2,3Tong Juanjuan1Li Jun1Wang Jin1Gu Chen1Lu Jinhui1

(1School of Electronic and Optical Engineering, Nanjing University of Science and Technology, Nanjing 210094, China)(2National Mobile Communications Research Laboratory, Southeast University, Nanjing 210096, China)(3Ministerial Key Laboratory of JGMT, Nanjing University of Science and Technology, Nanjing 210094, China)

A pilot pattern across two orthogonal frequency division multiplexing (OFDM) symbols with a special structure is designed for the channel estimation of OFDM systems with inphase and quadrature (IQ) imbalances at the receiver. A high-efficiency time-domain (TD) least square (LS) channel estimator and a low-complexity frequency-domain Gaussian elimination (GE) equalizer are proposed to eliminate IQ distortion. The former estimator can significantly suppress channel noise by a factorN/(L+1) over the existing frequency-domain (FD) LS, whereNandL+1 are the total number of subcarriers and the length of cyclic prefix, and the proposed GE requires only 2Ncomplex multiplications per OFDM symbol. Simulation results show that by exploiting the TD property of the channel, the proposed TD-LS channel estimator obtains a significant signal-to-noise ratio gain over the existing FD-LS one, whereas the proposed low-complexity GE compensation achieves the same bit error rate (BER) performance as the existing LS one.

inphase and quadrature (IQ) imbalance; equalizer; channel estimation; time domain; frequency domain; least square

Orthogonal frequency division multiplexing (OFDM) has been adopted by several standards such as LTE/LTE-advanced, wireless local area network (IEEE 802.11a, g and n), wireless metropolitan area network (IEEE 802.16d, e and m), digital audio broadcasting, DVB-T/C, digital radio mondiale and digital video broadcasting. Compared with the heterodyne receiver, the receiving RF architecture of direct conversion has been recently reconsidered as a promising solution in OFDM systems to reduce the cost and power consumption of the receiver[1-3]. However, the receiving RF architecture of direct conversion is severely distorted by gain and phase imbalances between the I and Q paths due to imperfections of the analog component design[1-3]. This will seriously damage the orthogonality among subcarriers in OFDM systems and yield inter-carrier interference, which will form a large bit error rate (BER) floor. Therefore, the estimation and compensation of IQ imbalance in the direct conversion receivers are extremely important for improving system performance.

The schemes for cancelling IQ imbalance have been investigated by several scholars. In Ref.[1], the authors derived the signal-to-noise ratio (SNR) loss of IQ imbalances in OFDM receivers and proposed several frequency-domain (FD) and time-domain (TD) compensation methods, such as post-FFT least-squares, adaptive least mean square (LMS) and pre-FFT TD compensation to eliminate IQ distortions. These methods were extended to IQ imbalances at both the transmitter and the receiver[4]. Blind estimation and compensation schemes in the time domain were also proposed[5]. The joint estimation of the IQ imbalance and several other impairments such as phase noise and frequency offset were investigated in Refs.[6-10]. In Ref.[6], a finite impulse response (FIR) filter followed by an asymmetric phase compensator was proposed to correct both frequency dependent and frequency independent IQ imbalances. In Ref.[8], a differential filter was employed to estimate both frequency offset and IQ imbalance. A compensation method based on the subcarrier allocation of OFDM signals was proposed in Ref.[9]. Feigin et al.[11]extended the research of Tx/Rx IQ imbalances to the case of packet-switched systems. Narasimhan et al.[12-13]focused on pilot designs and reduced complexity compensation in MIMO-OFDM systems with IQ imbalances. Gregorio et al.[14]proposed a MIMO-PD (pre-distorter) that compensates both crosstalk and IQ imbalance in MIMO-OFDM systems. In Ref.[15], the digital compensation of both the transmitter and the receiver IQ imbalances in MIMO-OFDM transmission over doubly selective channels was studied, and two receiver schemes were proposed to simultaneously mitigate the IQ imbalance and channel time variation effects by using a novel IQ formulation. In Ref.[16], the authors proposed two pre-compensation algorithms with and without IQ imbalance parameters in order to compensate for the channel non-reciprocity caused by a frequency-independent IQ imbalance. In Ref.[17], authors utilized convex optimization methods to optimize the power of all active subcarriers, and employed the adaptive Markov chain Monte Carlo model to select a training sequence to minimize the mean square error (MSE) of the channel estimator while suppressing the effect of the IQ imbalance. Additionally, a joint estimation of IQ imbalance and channel impulse response was proposed in Ref.[18] for MIMO-OFDM systems.

Unfortunately, in Ref.[1], the FD-LS channel estimation did not exploit the TD property of the channel with IQ imbalance. Thus, it required more than twenty training OFDM symbols to achieve the BER performance of ideal channel knowledge with no IQ imbalances (abbreviated as ideal IQ below). Clearly, this scheme had a low bandwidth efficiency. To solve this problem, an LS channel estimator has been designed, which fully exploits the TD property of channel parameters and significantly reduces the impact of channel noise. Also, it requires only two OFDM symbols to obtain the BER performance of the system without IQ imbalances. It should be noted that “equalizer” is equivalent to “compensation” in this paper.

1 System Model

In the OFDM systems with IQ imbalance as shown in Fig.1, an OFDM symbol hasNsubcarriers, and the transmitted block ofNdata symbols overNsubcarriers is denoted as

s=[s(1),s(2),…,s(N)]T

(1)

Taking IDFT operation on Eq.(1) yields

(2)

where

m,n∈{1,2,…,N}

(3)

Then, the received OFDM symbol before being distorted by IQ imbalance is expressed as

(4)

whereΛ=diag{H}, and

(5)

whereh=[h(1),h(2),…,h(L+1)]Tis the channel impulse response (CIR). The received OFDM symbol after being distorted by IQ imbalance is written as

(6)

Fig.1 Discrete baseband OFDM systems with an IQ imbalance at the receiver

whereμ=cos(θ/2)+jαsin(θ/2) andν=αcos(θ/2)-jsin(θ/2) withθandαbeing phase and amplitude imbalances between I and Q branches[1], respectively. Taking FFT operation on Eq.(6) gives

z=μdiag{H}s+νdiag{H#}s#+w

(7)

where the operation # is defined as[1]

X#=[X*(1),X*(N),…,X*(N/2+2),X*(N/2+1),

X*(N/2),…,X*(2)]T

(8)

with

X=[X(1),X(2),…,X(N/2),X(N/2+1),

X(N/2+2),…,X(N)]T

(9)

From Ref.[1], ifX=Fx, then

X#=(Fx)#=Fx*

(10)

Thus, we obtain the following identity:

(X#)#=(Fx*)#=Fx**=X

(11)

In the following, channelhis assumed to be constant during one frame and changes from one frame to another.

2 Proposed Pilot Pattern, Channel Estimator and Equalizer

In the following, a low-complexity Gaussian elimination is proposed to cancel the IQ distortion by using operation #. Then, a particular training pattern using two adjacent OFDM symbols is designed and a TD-LS channel estimation is presented to provide a high-precision estimation of the channel parametersν/μ*,μHandν*H. Additionally, the estimation ofμHandν*Hby the FD-LS in Ref.[1] is also transformed to the time domain and again back to the frequency domain to improve the accuracy of the estimation.

2.1 Gaussian elimination equalizer in FD

Since (diag{H}s)#=diag{H#}s#and (diag{H#}s#)#=diag{H}s, making a mathematical operation # on Eq.(7) yields

z#=ν*diag{H}s+μ*diag{H}#s#+w#

(12)

Definingκ=ν/μ*which can be estimated by existing channel estimators, based on Eqs.(7) and (12), we construct the following formula:

z-κz#=(μ-κν*)diag{H}s+w-κw#

(13)

which has removed the IQ distortion in Eq.(7) and it is represented as

z-κz#=(diag{μH}-κdiag{ν*H})s+w-κw#

(14)

Eq.(14) yields the following detector as

(15)

which can be simplified as

(16)

To complete the detection ofsin Eqs.(15) or (16), we need to estimate parametersκ,μH, andν*Hin advance, where

(17)

(18)

It should be noted that Eqs.(17) and (18) are the building blocks of channel estimation in Section 1.

gloss=

(19)

where Re(x) denotes the real part ofx.

2.2 Pilot pattern design and TD-LS estimation of channel parameters

Let us devise the frequency-domain pilot vectors of two pilot OFDM symbols at the start of a frame as

z1(2:N/2)=μdiag{H(2:N/2)}sp+w1(2:N/2)

(20)

w1(N/2+2:N)

(21)

(22)

z2(N/2+2:N)=μdiag{H(N/2+2:N)}sp+

w2(N/2+2:N)

(23)

and

z1(1)=μH(1)η+νH(1)*η+w1(1)

(24)

z1(N/2+1)=μH(N/2+1)η+νH(N/2+1)*η+

w1(N/2+1)

(25)

z2(1)=jμH(1)η-jνH(1)*η+w2(1)

(26)

z2(N/2+1)=jμH(N/2+1)η-jνH(N/2+1)*η+

w2(N/2+1)

(27)

Then, combining Eqs.(24) to (27) forms the following equations:

-0.5jz2(1)+0.5z1(1)=μH(1)η-0.5jw2(1)+0.5w1(1)

(28)

0.5jz2(1)+0.5z1(1)=νH(1)*η+0.5jw2(1)+0.5w1(1)

(29)

-0.5jz2(N/2+1)+0.5z1(N/2+1)=μH(N/2+1)η-

0.5jw2(N/2+1)+0.5w1(N/2+1)

(30)

0.5jz2(N/2+1)+0.5z1(N/2+1)=νH(N/2+1)*η+

0.5jw2(N/2+1)+0.5w1(N/2+1)

(31)

Stacking Eqs.(20), (23), (28) and (30) gives a large matrix-vector form as

(32)

Thus, the TD-LS estimate ofμhis given as

(33)

whereP=[IL+10(L+1)×(N-L-1)]. Then, we have the estimate ofμHas

(34)

In the same way, we combine Eqs.(21), (22), (29) and (31) into a large matrix-vector form

(35)

whose # operation forms

(36)

and Eq.(36) results in the LS estimation ofν*h.

(37)

Then, we have the estimate ofν*Has

(38)

In terms of Eqs.(33), (34), (37), and (38), the estimate ofκcan be defined as

(39)

From Eqs.(33), (34), (37) and (38), we obtain the MSEs ofν*HandμHas follows:

(40)

(41)

3 Simulation and Discussion

In the following, a typical OFDM system is used to evaluate the performance of the proposed channel estimator, the proposed compensation method and those existing channel estimations and compensation schemes. An ideal OFDM receiver with no IQ imbalance and a receiver with no compensation are used as performance references. It is noted that A stands for the channel estimator and B denotes the equalizer below.

Simulation parameters are as follows: The OFDM symbol lengthN=128, cyclic prefixL=16, signal bandwidth BW=2 MHz, digital modulation QPSK, and the carrier frequencyfc=2 GHz. Channelhis selected to be the typical urban (TU) channel.

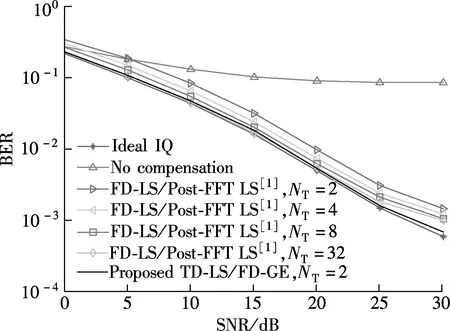
Fig.2 compares the proposed schemes with the FD-LS channel estimator plus the Post-FFT LS equalizer (FD-LS/Post-FFT) for different values of IQ imbalance parameters whereNTdenotes the number of training OFDM symbols (TOSs) per frame. From these figures, it is evident that the proposed joint scheme of the TD-LS estimator plus GE equalizer, with only two TOSs, can achieve the BER performance of ideal IQ at low and medium SNRs, whereas the joint scheme of the FD-LS estimator plus the LS equalizer in Ref.[1] costs approximately 32 TOSs to realize almost the same BER performance. Thus, the proposed scheme has a higher bandwidth efficiency compared to the FD-LS estimator plus the LS equalizer.

Tab.1 makes a complexity comparison of four schemes including the proposed scheme of TD-LS/GE, and the existing schemes of FD-LS/Post-FFT, FD-LS/Pre-FFT Corr, and SPP/Pre-FFT Corr in Ref.[1], whereNFis the total number of non-training OFDM symbols. The TD-LS/GE scheme put forward has almost the same computational amount as the three existing schemes.

Tab.1 Complexity comparison for five schemes of channel estimation plus compensation

(a)

(b)

(c)

4 Conclusion

In this paper, a joint scheme of combining a TD-LS channel estimator and a FD-GE equalizer is investigated in OFDM systems with IQ imbalance at the receiver. Compared with the existing schemes such as FD-LS/Post-FFT LS, SPP/Pre-FFT Corr and FD-LS/Pre-FFT Corr in Ref.[1], this scheme shows much better BER performance. More importantly, it requires only two OFDM training symbols to achieve the BER performance of the ideal IQ at low and medium SNR regions, whereas three existing schemes, including FD-LS/Post-FFT LS, SPP/Pre-FFT Corr and FD-LS/Pre-FFT Corr, require around twenty OFDM training symbols to achieve the same BER. Concerning complexity, the proposed TD-LS/FD-GE has the same as the existing schemes.

[1]Tarighat A, Bagheri R, Sayed A H. Compensation schemes and performance analysis of IQ imbalances in OFDM receivers[J].IEEETransactionsonSignalProcessing, 2005, 53(8): 3257-3268.

[2]Razavi B, Behzad R.RFmicroelectronics[M]. New Jersey: Prentice Hall, 1998.

[3]Abidi A A. Direct-conversion radio transceivers for digital communications[J].IEEEJournalofSolid-StateCircuits, 1995, 30(12): 1399-1410.

[4]Tarighat A, Sayed A H. Joint compensation of transmitter and receiver impairments in OFDM systems[J].IEEETransactionsonWirelessCommunications, 2007, 6(1): 240-247.

[5]Valkama M, Renfors M, Koivunen V. Advanced methods for I/Q imbalance compensation in communication receivers[J].IEEETransactionsonSignalProcessing, 2001, 49(10): 2335-2344.

[6]Xing G, Shen M, Liu H. Frequency offset and I/Q imbalance compensation for direct-conversion receivers[J].IEEETransactionsonWirelessCommunications, 2005, 4(2): 673-680.

[7]Tubbax J, Come B, Van der Perre L, et al. Compensation of IQ imbalance and phase noise in OFDM systems[J].IEEETransactionsonWirelessCommunications, 2005, 4(3): 872-877.

[8]Inamori M, Bostamam A, Sanada Y, et al. IQ imbalance compensation scheme in the presence of frequency offset and dynamic DC offset for a direct conversion receiver[J].IEEETransactionsonWirelessCommunications, 2009, 8(5): 2214-2220.

[9]Lin H, Yamashita K. Subcarrier allocation based compensation for carrier frequency offset and I/Q imbalances in OFDM systems[J].IEEETransactionsonWirelessCommunications, 2009, 8(1): 18-23.

[10]Tandur D, Moonen M. Joint adaptive compensation of transmitter and receiver IQ imbalance under carrier frequency offset in OFDM-based systems[J].IEEETransactionsonSignalProcessing, 2007, 55(11): 5246-5252.

[11]Feigin J, Brady D. Joint transmitter/receiver I/Q imbalance compensation for direct conversion OFDM in packet-switched multipath environments[J].IEEETransactionsonSignalProcessing, 2009, 57(11): 4588-4593.

[12]Narasimhan B, Narayanan S, Minn H, et al. Reduced-complexity baseband compensation of joint Tx/Rx I/Q imbalance in mobile MIMO-OFDM[J].IEEETransactionsonWirelessCommunications, 2010, 9(5): 1720-1728.

[13]Minn H, Munoz D. Pilot designs for channel estimation of MIMO OFDM systems with frequency-dependent I/Q imbalances[J].IEEETransactionsonCommunications, 2010, 58(8): 2252-2264.

[14]Gregorio F, Cousseau J, Werner S, et al. Compensation of IQ imbalance and transmitter nonlinearities in broadband MIMO-OFDM[C]//2011IEEEInternationalSymposiumonCircuitsandSystems. Rio de Janeiro, Brazil, 2011: 2393-2396.

[15]Beheshti M, Omidi M J, Doost-Hoseini A M. Joint compensation of transmitter and receiver IQ imbalance for MIMO-OFDM over doubly selective channels[J].WirelessPersonalCommunications, 2013, 70(2): 537-559.

[16]Liu Z J, Sun D C, Wang J L, et al. Impact and compensation of I/Q imbalance on channel reciprocity of time-division-duplexing multiple-input multiple-output systems[J].IETCommunications, 2013, 7(7): 663-672.

[17]Manasseh E, Ohno S, Yamamoto T. Efficient training design for estimation of channel, CFO, and receiver I/Q imbalance in MIMO-OFDM systems[C]//2013 13thInternationalSymposiumonCommunicationsandInformationTechnologies. Surat Thani, Thailand, 2013: 364-368.

[18]Deng J H, Hsieh H S, Feng K T. Low complexity I/Q imbalance and channel estimation techniques for MIMO OFDM systems[C]//2013 15thIEEEInternationalConferenceonAdvancedCommunicationTechnology. Pyeongchang, Korea, 2013: 238-243.

[19]Edfors O, Sandell M, Van de Beek J J, et al. OFDM channel estimation by singular value decomposition[J].IEEETransactionsonCommunications, 1998, 46(7): 931-939.

接收IQ不平衡OFDM系统的高性能信道估计和补偿方案

束 锋1,2,3童娟娟1李 隽1王 进1顾 晨1陆锦辉1

(1南京理工大学电子工程与光电技术学院,南京210094)(2东南大学移动通信国家重点实验室,南京210096)(3南京理工大学近程高速目标探测技术国防重点学科实验室,南京210094)

针对接收IQ不平衡的OFDM系统,设计了横跨2个OFDM符号的特殊训练结构．提出了一种高效的时域最小二乘(TD-LS)信道估计和一种低复杂度的频域高斯消元补偿算法来消除IQ失真．前者与传统的频域LS算法相比,信道估计噪声的影响降低了N/(L+1)倍,其中N为子载波总数,L+1为循环前缀长度;后者实现复杂度低,每个OFDM符号仅需要2N次复数乘法．仿真结果表明:由于充分挖掘了信道参数的时域特性,提出的TD-LS信道估计算法与传统的FD-LS算法相比获得了可观的信噪比增益；提出的低复杂度的GE补偿算法能够获得与基于LS的频域补偿方案几乎相同的误码性能．

IQ不平衡;均衡器;信道估计;时域;频域;最小二乘

TN929.5

Received 2014-04-20．

Biography：Shu Feng (1973—), male, doctor, professor, shufeng@njust.edu.cn.

s：The Open Research Fund of National Mobile Communications Research Laboratory of Southeast University (No.2013D02), the Fundamental Research Funds for the Central Universities (No.30920130122004), the National Natural Science Foundation of China (No.61271230, 61472190).

：Shu Feng, Tong Juanjuan, Li Jun, et al．High-performance channel estimation and compensation scheme for OFDM receivers with IQ imbalances[J]．Journal of Southeast University (English Edition),2014,30(4):416-421．

10.3969/j.issn.1003-7985.2014.04.003

10.3969/j.issn.1003-7985.2014.04.003