TVD格式数值模拟水电站水击波新探
2014-09-06范晓丹刘韩生
范晓丹,刘韩生,董 瑜,张 丹
(1.西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100;2.湖北省水利水电科学研究院, 湖北 武汉 430070)
TVD格式数值模拟水电站水击波新探
范晓丹1,刘韩生1,董瑜1,张丹2
(1.西北农林科技大学 水利与建筑工程学院, 陕西 杨凌 712100;2.湖北省水利水电科学研究院, 湖北 武汉 430070)
摘要:水电站有压管道水击波数值模拟十分重要,其计算方法一直都是重点研究方向,TVD格式是数值模拟水击波的新方法,特别适合数值模拟强间断问题。其限制函数是该格式的核心问题,具有四种不同形式,将其运用于水击方程,数值模拟阀门突然关闭时水击波压力变化,与解析解进行对比,以此探究限制函数类型对TVD数值模拟水击波结果的影响。结果表明:四种限制函数TVD格式的计算结果,在间断处避免了非物理振荡,Superbee型TVD格式的分辨率最高,推荐该限制函数数值模拟水电站水击波。
关键词:限制函数;TVD格式;数值模拟;非物理振荡;水击
自1983年Harten在文献[1]中提出TVD格式以来,TVD格式就以其具有模拟大梯度流动和自动捕捉激波的能力,在计算空气动力学及溃坝水力学[2]中得到了广泛应用。在水电站和水利枢纽等给水管道系统设计和操作中,水击是考虑的重要因素之一,而数值模拟是进行水击计算的常用方法。本文选用近年来广泛用于空气动力学和溃坝水力学中模拟激波的TVD[3]格式进行计算。对于水击波数值模拟,文献[4-7]表明TVD格式较常规的差分格式有显著的优势,表现在间断处TVD格式数值模拟的分辨率显著提高,常规的差分方法,一阶格式在间断处坦化,二阶格式则出现显著的非物理振荡。这些文献用单一的TVD数值计算,没有论证TVD格式之间的区别。事实上,TVD格式有多种形式,常用的限制函数有四种,本文分别采用这四种限制函数进行数值计算,比较计算结果,推荐采用Superbee型限制函数。
1 控制方程
计算流体力学中,与解析解对比是论证格式优劣的有效方法,对于水电站水击波问题选用忽略摩阻损失及管道倾斜影响的简化水击基本微分方程作为控制方程,其为一维简化且有解析解的常系数双曲型偏微分方程组[8],即:
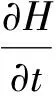
(1)
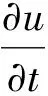
(2)
式中:H为测压管水头;u为断面平均流速;c为水击波速。
方程式(1)和式(2)可以写成式(3)的形式:
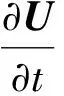
(3)
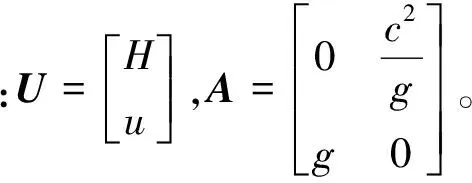

(4)
式中:F=AU。
2 计算格式
近年来TVD格式有了许多新进展,文献[9]中的TVD格式比较常用,适合计算拟线性双曲型偏微分方程,其形式如下:
(5)
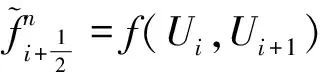
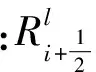
但是从读者利用图书馆的信息行为来看,出现了借书量逐年下降、查找资料首选不一定是图书馆、入馆人次减少、对图书馆的利用以自习为主、传统咨询量减少、数字资源利用率在提高等变化。以陕西省7所211大学图书馆为例,从2011年到2016年,图书外借量均出现1万-32万不等的数量减少。

3 限制函数
为了使离散化方程自动高分辨率的捕捉间断解,自适应调节数值耗散和数值色散效应,并保持格式的单调性,19世纪70年代一个非线性函数φ(r)被提出,又称通量限制器(flux limiter)[10],即限制函数。引入限制函数,可真正的对解的间断和大梯度的地方给出尖锐的图像,即如果未知函数的离散近似解有很大的梯度或振幅趋势,它可以适当的加强数值粘性;反之,在比较平坦的地方可以降低数值耗散,甚至局部引入反耗散机制,从而达到间断数值解的高分辨率。
二阶TVD格式的φ(r)常表示为压缩参数Φ的函数,其整个区域可统一表示为φ(r)=max〔0,min(1,Φr),min(Φ,r)〕,1≤Φ≤2,在允许区域内选取不同的非线性限制函数φ(r),建立起不同性能的二阶TVD格式。本文对每一种一阶逆风格式采用以下4种限制函数建立四种二阶TVD格式,如下所示[11]:
(1)Roe的Minmod型:φ(r)=min mod(1,r)

(3)VanLeer的Muscl型:
φ(r)=max{0,min〔2,2r,0.5(1+r)〕}
(4)Roe的Superbee型:
φ(r)=max〔0,min(2r,1),min(r,2)〕
其中:Superbee限制函数为整个允许区域的上边界,Minmod限制函数为整个允许区域的下边界,VanLeer的Monotonic型限制函数为该区域内的一条光滑的弧线,VanLeer的Muscl型限制函数耗散性与压制性适中。此外,VanLeer限制函数单调递增且具有对称性。可以看出,4种限制函数均满足φ(1)=1,这正是数值通量达到二阶精度所需满足的总体要求。
4 边界条件[12]
对于管道上游端接大水库的情况,在很短的瞬变期间通常可以假定水库水位是恒定不变的。所以,上游的边界条件是:水击波的传播过程中,进口断面的水头保持为常数[13],即:
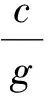
(6)
因而可得入口的流速为:

(7)
4.2管道末端断面边界条件
管道末端断面与流量控制设备相连,故该断面的流动条件与设备控制的类型及其控制规律有关。不同类型的水电站水轮机其流量控制设备也各不相同,所以边界条件往往比较复杂。在此,仅讨论一种比较简单的情况——管道末端与阀门相连。

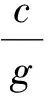
(8)
从而可得:
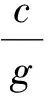
(9)
如果下游给定阀门边界条件,根据孔口出流规律可以确定水头和流量之间的关系为:
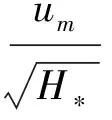
(10)
式中:um为阀门全开时管道中的流速;τi为i时刻管道阀门的相对开度,0<τi<1;H*为阀门在恒定流状态下管道末端的水头。如果下游为阀门瞬时关闭的理想工况,则τi=0,可得下游流速边界条件为uN=0。
4.3次边界条件的处理
由于本文所用TVD格式是五点格式,涉及到次边界点的计算,常见的处理方法是将次边界点改为三点格式。
5 算 例
某压力钢管,上游与水库相接,下游接冲击式水轮机的控制阀门。已知:压力钢管的长度L=600 m,管径D=2 400 mm,管壁厚度δ=20 mm,水头H0=200 m,阀门全开时管道中最大流速vm=3 m/s。若规定阀门启闭时间Ts=1 s,试求阀门由完全开启至完全关闭情况下,管道末端阀门处的最大水头和最低水头。
经计算知,阀门断面发生直接水击,此时可认为管道压力和流速的初始值在阀门断面处存在间断。
计算模型如图1所示。

图1计算模型
首先计算水击波的解析解,然后分别采用四种制函数的TVD格式进行编程计算,将结果与解析解绘图对比如图2~图4所示。

图2Minmod型与解析解
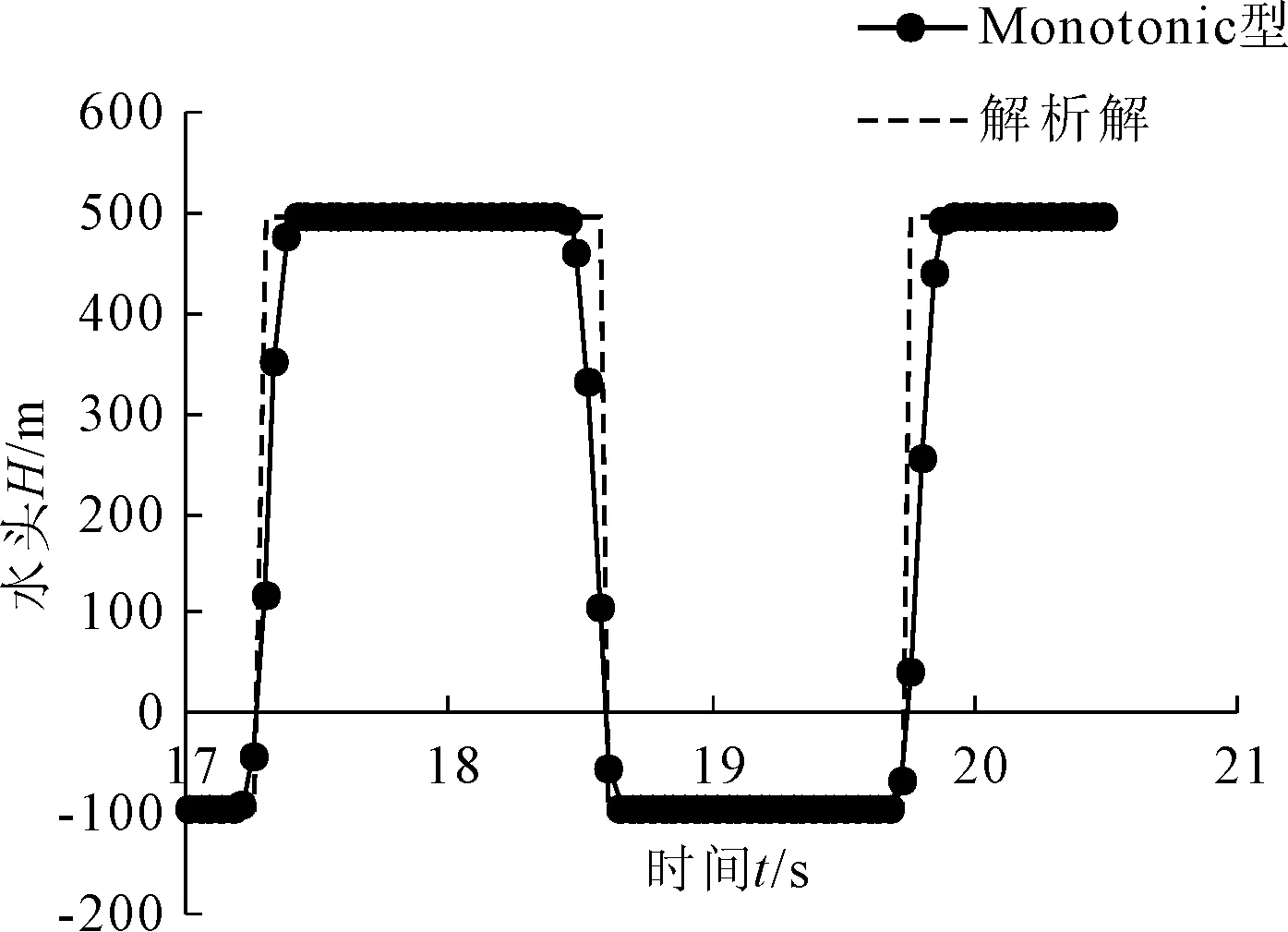
图3Monotonic型与解析解
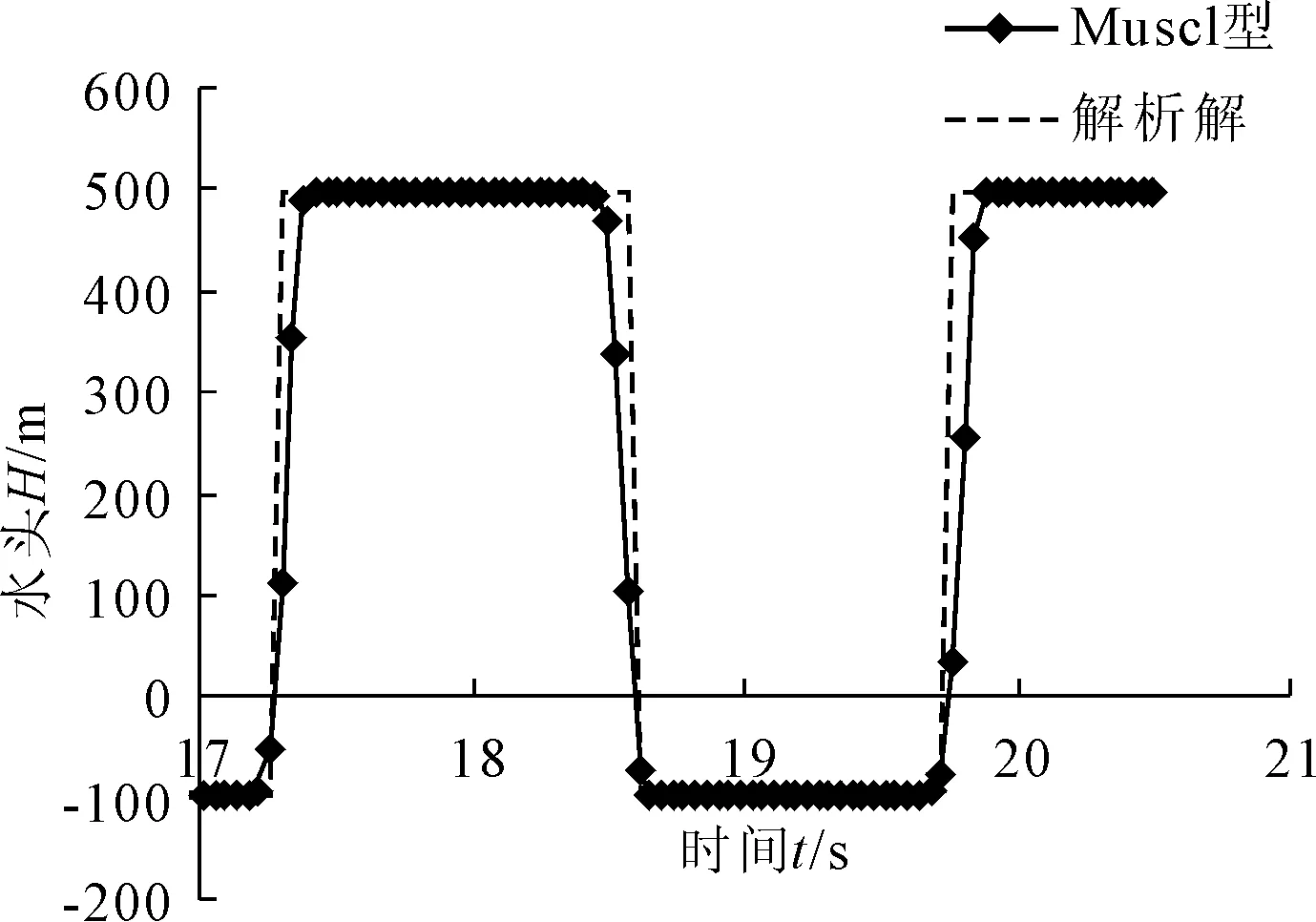
图4Muscl型与解析解

图5Superbee型与解析解
由图中可以看出:4种限制函数TVD格式的计算结果有两个明显的特点:一是在光滑区计算结果理想,计算值与解析值完全吻合;二是在间断处避免了非物理振荡,这种振荡在两阶差分格式是无法避免的,即使设置人工粘性,也只能限制振荡,不能避免,而此处的TVD格式为两阶精度,能够避免这种非物理振荡,发挥了其变差不增的优势。
在间断处,TVD格式降为一阶精度[14],使得间断处微有坦化现象,这是正常的,与一阶差分格式的坦化比较,这里的坦化微不足道。高分辨格式能够在很窄的网格范围内分辨出间断解而不产生数值振荡,4种限制函数TVD格式的分辨率均不超过5个网格,体现了TVD格式的高分辨率性能[15];4种格式相互比较,Superbee型TVD格式的分辨率最高,为3个网格,其它3个限制函数的分辨率基本相同为4~5个网格,故推荐Superbee型TVD格式数值模拟水电站水击波。
6 结 论
(1)4种限制函数TVD格式的计算结果在光滑区计算值与解析完全吻合,在间断处避免了非物理振荡,且呈现高分辨率特性。
(2)4种限制函数TVD格式的计算结果表明,Sweby 的Superbee型限量函数的TVD格式对间断的分辨率最高,具有相对最强的激波捕捉能力,对水击过程的模拟最为逼真,推荐该限制函数数值模拟水电站水击波。
参考文献:
[1]Harten A. High resolution schemes for hyperbolic conservation laws[J]. Journal of Computational Physics,1983,49(3):357-363.
[2]王嘉松.TVD格式数值模拟溃坝波的研究[D].大连:大连理工大学,1998.
[3]刘儒勋,舒其望.计算流体力学的若干新方法[M].北京:科学出版社,2003.
[4]樊书刚,刘韩生,张丹,等.TVD格式在水击数值模拟中的应用[J].水力发电学报,2010,(4):107-112.
[5]樊书刚,刘韩生,张一.一维水击波的高精度数值模拟[J].水力发电,2010,36(4):79-81.
[6]张丹,刘韩生,李顺兵.水击的数值模拟方法比较[J].人民长江,2008,39(18):75-76
[7]张丹.TVD格式数值模拟水击波过程研究[D].杨凌:西北农林科技大学,2009.
[8]吕宏兴,裴国霞,杨玲霞.水力学[M].北京:中国农业出版社,2002.
[9]王嘉松,倪汉根,金生.瞬间全溃溃坝波的传播、反射和绕射的数值模拟[J].水动力学研究与进展,2000,15(3):1-7.
[10]Van Leer B. Towards the ultimate conservation difference scheme[J]. Journal of Computational Physics,1997,135(2):229-248.
[11]徐文灿,胡俊.计算流体力学[M].北京:北京理工大学出版社,2012.
[12]樊书刚,刘韩生.基于ENO格式的一维水击波数值模拟[J].人民黄河,2010,32(3):102-103
[13]郭维东,裴国霞,韩会玲.水力学[M].北京:中国水利水电出版社,2005.
[14]倪汉根,王嘉松.线性双曲型方程新的TVD格式[J].计算物理,1999,16(1):25-30.
[15]胡四一,谭维炎.用TVD格式预测溃坝洪水波的演进[J].水利学报,1989,(7):1-11.
NewStudyonNumericalSimulationofWaterHammerWavesofHydropowerStationswithTVDScheme
FAN Xiao-dan1,LIU Han-sheng1,DONG Yu1,ZHANG Dan2
(1.CollegeofWaterResourcesandArchitecturalEngineering,NorthwestA&FUniversity,Yangling,Shaanxi712100,China;2.HubeiWaterResourcesResearchInstitute,Wuhan,Hubei430070,China)
Abstract:The numerical simulation of water hammer waves in pressure pipes of hydropower stations is very important. Its calculation method has always been a key research issue. TVD scheme is a new method to simulate water hammer waves with its strength in simulating strong discontinutity problems. The limiter function which possesses four different forms is the essence of the scheme. Here,they were applied to the water hammer equation to simulate the variations of surge pressure when the valve suddenly closed. In order to discuss the effect that the type of limiter function had on the results of water hammer waves’numerical simulation with TVD scheme,the results of numerical simulation were compared with that of the analytical solutions. It indicates that the calculations of TVD scheme with four limiter functions can avoid numerical oscillations at discontinuity point. The TVD scheme with Superbee limiter fountion has the highest resolution and it is recommended for simulating water hammer waves of hydropower stations.
Keywords:limiter fountion;TVD scheme;numerical simulation;numerical oscillations;water hammer
DOI:10.3969/j.issn.1672-1144.2014.05.038
中图分类号:TV131.61
文献标识码:A
文章编号:1672—1144(2014)05—0185—04
作者简介:范晓丹(1992—),女,河南南阳人,本科生,水利水电工程专业。通讯作者:刘韩生(1962—),男,陕西韩城人,教授,硕士生导师,主要从事水力学与水工建筑物方面的研究工作。
收稿日期:2014-05-07修稿日期:2014-06-01
