高墩大跨连续刚构桥悬臂施工过程中的预拱度设置研究
2014-09-06成仲鹏
成仲鹏,贾 斌,陈 彪
(1.兰州交通大学 土木工程学院, 甘肃 兰州 730070;2.中铁一院新疆铁道勘察设计院有限公司, 新疆 乌鲁木齐 830011)
高墩大跨连续刚构桥悬臂施工过程中的预拱度设置研究
成仲鹏1,贾斌1,陈彪2
(1.兰州交通大学 土木工程学院, 甘肃 兰州 730070;2.中铁一院新疆铁道勘察设计院有限公司, 新疆 乌鲁木齐 830011)
摘要:分析了在悬臂浇筑施工过程中影响梁体挠度的主要因素,根据桥梁结构理论计算方法,得出了在相应荷载作用下挠度的计算公式,对各施工阶段的梁体挠度进行合理的计算,再通过设置相应的预拱度,控制桥梁的施工线形。最后通过实际工程算例,证明了此方法设置预拱度的合理性,为以后同类桥梁的预拱度设置提供依据。
关键词:桥梁工程;预拱度;悬臂施工;高墩大跨连续刚构
大跨度连续刚构桥目前主要采用挂篮平衡悬臂施工[1],对于悬臂施工的桥梁,施工过程中各梁段挠度的分析与控制是施工控制的关键内容[2]。若预拱度设置不合理,将直接影响到每一阶段梁体的立模标高,影响桥梁的施工线形、合拢精度以及桥梁的成桥线形。在自重作用下,梁段会产生向下挠度;随着钢绞线的张拉,梁体会产生向上的变形;由于混凝土材料本身的性质,在施工过程中及成桥后结构会产生一定的收缩徐变变形[3]。此外,桥梁的建设需要一个较长的工期,温度对梁体挠度的影响难以避免[4],如何量化温度变化引起梁体的变形,也是预拱度设置中的一个难题。还有,在施工过程中挂篮体系的变形,也会直接影响到现阶段梁体的标高。
文中对高墩大跨度连续梁桥悬臂施工过程中预拱度设置的因素进行了分析,根据桥梁结构理论计算方法[5],得出了各自条件下的挠度计算公式,为高墩大跨桥梁施工监控过程中预拱度的设置提供理论依据,保证成桥线形与设计线形相吻合。
1 悬臂施工过程中自重作用挠度计算
在实际工程计算中常采用一个简单的物理量间的关系来研究另一个复杂的物理量间的关系,在计算悬臂结构的挠度时也采用梁的挠曲线微分方程式与梁的弯矩函数M(x)和荷载密度函数q(x)间的关系式。由材料力学可知[6],在x=xi截面处梁的挠曲线微分方程为:
积分一次为:
积分两次为:


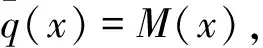
联立以上各式,有:
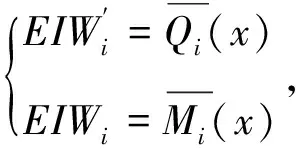
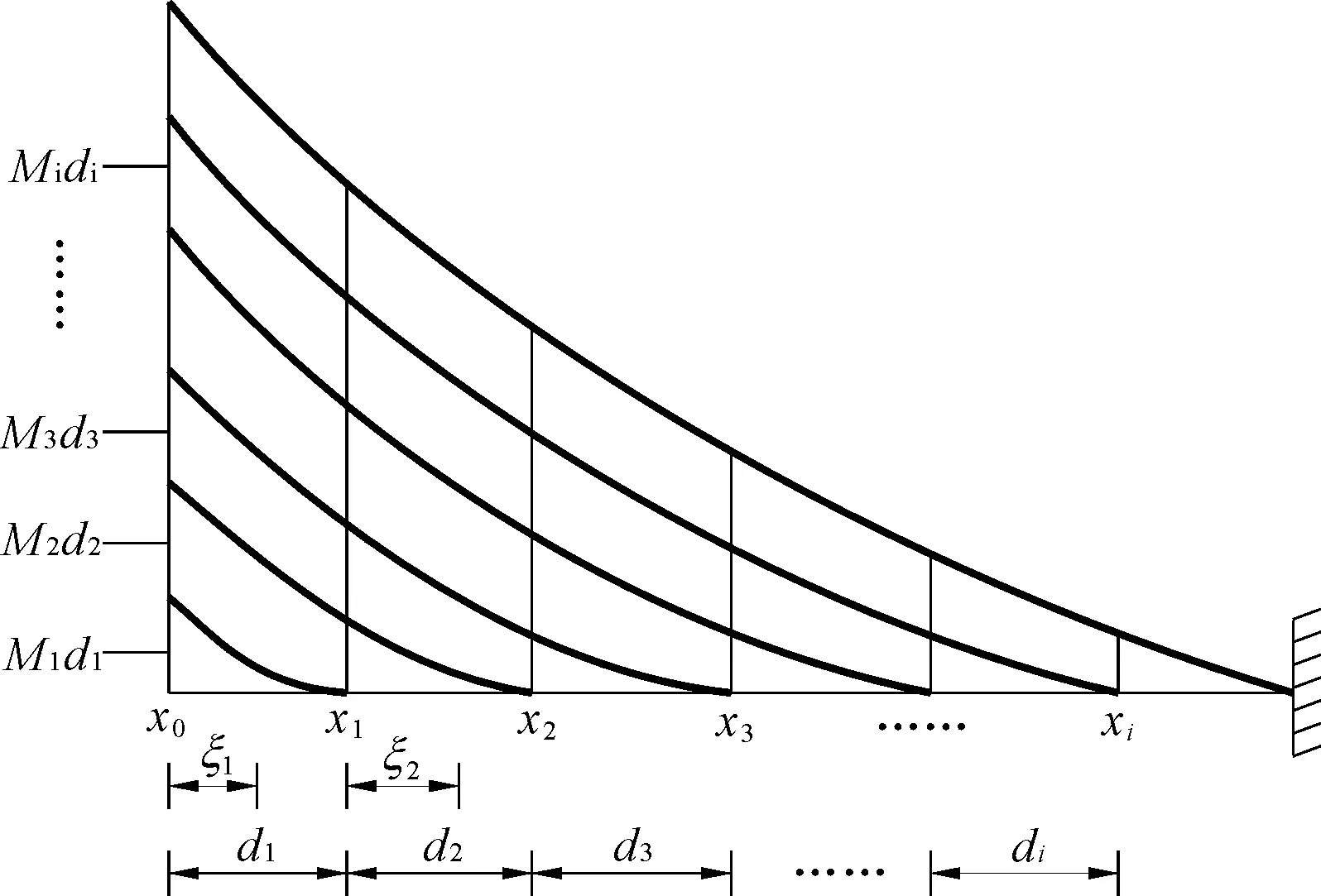
图1虚梁荷载集度
虚梁在x=xj截面处的虚弯矩为:
(1)


(2)
式中:Ei(m)表示在浇筑完第i梁段时第m梁段的弹性模量值;Im表示第m块梁段的抗弯惯性矩,一般取始末截面的算术平均值。
对于梁体的自重、预应力荷载[8]、挂篮自重作用等引起的挠度,通过换算为相应的弹性荷载,均可由上式求得。
2 悬臂施工过程中混凝土徐变挠度计算
采用悬臂浇筑施工方法的连续梁桥,混凝土的徐变性质在施工过程中会增大阶段梁体的挠度,造成施工误差偏大,在施工控制过程中必须考虑徐变效应。在计算施工过程中由于徐变引起结构的挠度时,既要考虑在施工过程中各种荷载条件,又要考虑各梁段逐段施工时混凝土加载龄期的差异。要精确分析结构徐变变形是十分困难的。在悬臂施工过程中,结构处于静定状态,根据弹性徐变理论[9],假设混凝土龄期为τ,结构内任意截面x=xj处的k点在t时刻由徐变引起的挠曲应变为:

再利用虚功原理计算结构在外荷载作用下x=xj截面徐变变形:
上式积分项表示在外荷载作用下x=xj截面所发生的弹性变形,由于采用分段施工,各梁段混凝土加载龄期有差异,再考虑E(t)随时间的变化,上式可改写为:

(3)
在结构发生体系转换之后,整个桥梁结构变为超静定结构,混凝土的徐变变形会引起结构的次内力,随着时间的推进,结构中应力是不断变化的,在以后的某一时刻,结构的徐变变形不再与应力保持线形关系。由于混凝土作用的龄期较长,为了简化计算,此时将混凝土的弹性模量假定为一定值。为了能够得到此阶段的徐变变形,Trost、Zema、Bazant等引入了时效系数[10],提出了“松弛系数法”,得出了在变化应力下,t时刻结构内下x=xj截面由于混凝土的徐变产生的变形为:
(4)
在悬臂施工过程中,随着时间的推移混凝土的徐变效应越来越明显。在进行徐变效应分析时,采用CEB-FIP(1990)收缩徐变模型[11],其所得的理论计算值与实测值最为接近,相比之下更适合于大跨度预应力混凝土连续梁在施工过程中的徐变效应分析。
3 悬臂施工过程中温差效应分析
桥梁结构是暴露在大气中的结构物,经历着复杂气候条件的变化。在日照作用下,因太阳辐射强度、桥梁方位等不确定性因素,在梁体和墩身中都会产生不均匀分布的温度场,对于正处于悬臂施工过程中的高墩大跨连续刚构桥来说,其产生的效应通常比恒载、活载更明显,在施工控制过程中必须重视[12-13]。
在进行结构温度应力分析时,为了方便计算,一般采用线形分布的温度梯度(见图2),这与实际的温度分布曲线有很大的差别。在此,文中基于等效原理,将实际环境中的非线性温度场转换成线形温度场进行温差效应分析。
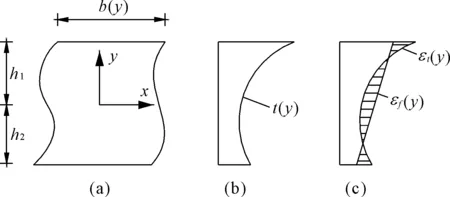
图2温度计算图式
在非线性温度梯度作用下,沿梁高度方向的应变分为两部分:
(1)自由应变(纵向纤维之间不受约束)εt(y),其与温度梯度一致,即:
εt(y)=αt(y)(α为线膨胀系数)
由于梁体的变形服从平截面假定,截面的实际变形可表示为:
εf(y)=ε0+φy(ε0为中性轴处的应变)
(2)由纵向纤维约束产生的应变(自应变)εσ(y)
εσ(y)=εt(y)-εf(y)=αt(y)-(ε0+φy)
相对应的应力为σ(y):
σ(y)=Eεσ(y)=E[αt(y)-(ε0+φy)]
此时全截面的轴力N和弯矩M为:
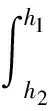
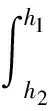
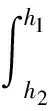
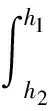
对于任意截面,有N=0M=0,代入有:
得出梁体顶、底面的应变为:
(5)
假设有一线形分布的温度梯度,梁顶温度为t1,梁底温度为t2,则沿梁高方向的应变为:
(6)
由公式(4)与公式(5)等效,可得:
(7)
通过上述换算,就把复杂的非线性分布的温度场近似的等效成线形分布的温度场,再根据变形体系的虚功原理及单位荷载法[14-15],可得梁体悬臂端日照温差偏移量计算公式为:
(8)
4 挂篮对梁体挠度的影响
挂篮体系在悬臂浇筑过程中的变形主要是弹性变形和几何变形。现浇梁段,在挂篮上浇筑后,刚度尚未形成,自重由挂篮承担。整个挂篮在现浇梁段自重作用下会产生一定的挠曲变形,使现浇梁段随之也产生与其相协调的变形,且这部分变形在挂篮拆除之后不可恢复。因此在预拱度设置中必须考虑这部分的影响;挂篮体系的几何变形影响因素较多,很难对其进行准确预测,一般通过对挂篮体系进行预压试验以消除其影响。此外,在悬臂施工过程中,挂篮本身自重也会使梁体产生竖向变形:对于已浇筑梁段,挂篮的自重会使其产生弹性变形,此时若将挂篮拆除,则弹性变形恢复,不必考虑其影响,但此部分变形对于现浇梁段的立模标高会产生影响,在预拱度设置时也必须考虑。根据公式(1)计算。
对于挂篮体系弹性挠度,可以通过对挂篮体系预压试验,提前预测出挂篮在各梁段自重作用下的理论变形值。在计算过程中将前吊带及其以上部分对底纵梁的影响等效为一刚度系数为k的弹簧,将底纵梁从后锚点到前吊点之间部分简化为图3形式力学计算图式。
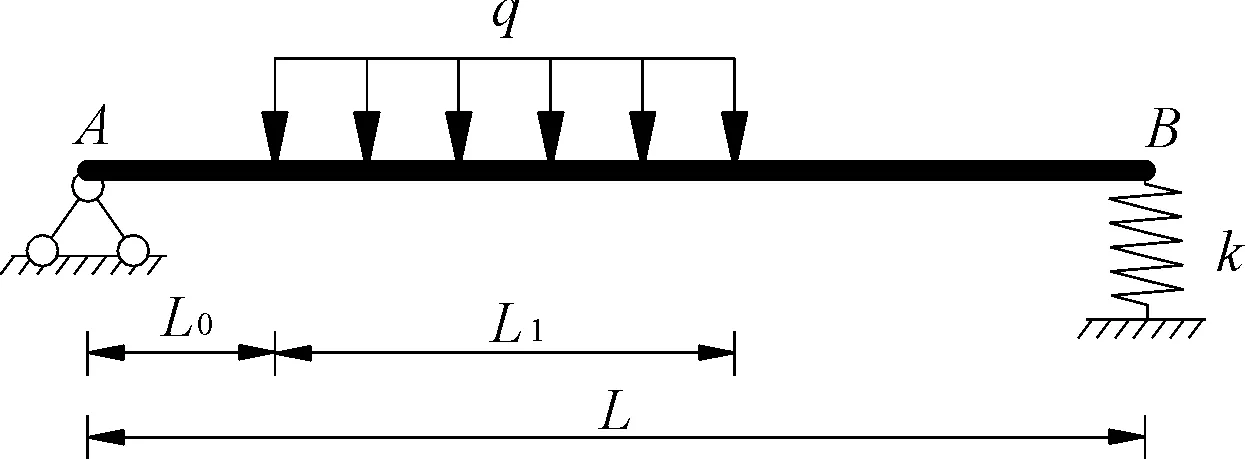
图3底纵梁力学计算图式
在预压试验过程中,根据现场预压荷载大小及加载位置,通过理论换算或在端头放置应力传感器,求出在预压荷载作用下B点所受的力FB,根据挠度数据得出B点处的变形Δl(扣除几何变形),可求的弹簧的等效刚度系数为:
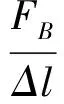
将各梁段自重等效为一均布荷载qi,则在qi作用下挂篮体系相应位置处的弹性变形值为:
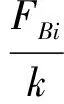
(9)
其中

式中:l0为底纵梁后锚点到已浇筑梁段端部的距离,一般取0.5 m;li为悬臂浇筑的梁段长;l为底纵梁后锚点到前吊点之间的长度。
上述计算公式只是理论计算,在实际施工过程中,还要根据现场实际测得的挂篮体系的变形数据进行调整。
5 墩身的弹性压缩及基础沉降引起的挠度计算
在高速铁路中,高速行驶的列车对线路的平顺性要求很高,在线路跨越深沟时,难免会采用高墩大跨桥梁结构。此类桥梁目前主要采用悬臂施工,在施工过程中,随着已成型梁体的不断延伸,作用在桥墩和基础上的力逐步增加。由于墩身较高,在轴力的作用下其会产生弹性压缩变形,这部分变形会以刚体位移的形式传递到悬臂端部,影响现阶段浇筑梁体的高程,致使与设计值发生偏差。墩身越高,偏差越严重。为了考虑墩身的弹性压缩及基础沉降值对阶段梁体标高的影响,在浇筑0#块的时候,通常设置一定量的墩顶预抛高Δl。其中Δl可按下式计算:

式中:M为对称悬臂施工梁段的总体积,包括0#块;A表示墩身的等效截面积;h表示墩高。
在计算出Δl之后,按照各块梁体的体积,分摊到每段梁体的立模标高中,即:

(10)
式中:Mi表示i梁段的体积。
以上主要分析了施工过程中预拱度设置需要考虑的主要因素,当然在预拱度的设置中还包括二期铺装产生的挠度。此外,根据规范要求,为了考虑后期运营过程中活载的效应,在设置预拱度时还需计入1/2静活载引起的挠度。下面就根据以上的理论分析,结合实际工程实例进行预拱度设置研究。
6 工程算例
某新建铁路货运专线中采用一座结构形式为(80+144+80)m的预应力混凝土连续刚构桥。主梁采用单箱单室变高度直腹板箱型截面,梁顶宽11.5 m,梁底宽7.2 m,墩顶梁高10.5 m,边跨直线段和合拢段梁高5.5 m;主墩采用双线圆弧端矩形空心墩,墩身高89 m。施工顺序为:1#~18#梁段对称施工,中跨合拢(20#梁段),中跨合拢之后浇筑边跨超打梁段(19#梁段),最后边跨合拢。根据施工阶段的划分,利用上述推导的公式设置相应的施工预拱度。通过测量桥梁合拢之后、二期恒载上桥之前桥面的预拱度,再结合此阶段相应的理论值进行分析比较。具体见图4所示。

图4桥面预拱度比较
由图4可以看出,桥梁合拢之后梁体实测的预拱度值均在理论值附近波动,曲线走向与理论值趋势相吻合,在施工过程中控制的精度较高;桥梁合拢之后,梁体仍有一定的预拱度,此部分预留值用于抵消二期荷载、运营过程中梁体的收缩徐变、活载作用下产生的挠度。从两条曲线的趋势可以得出,该桥在施工过程中预拱度设置合理,梁体线形控制较好。上述分析方法可以用于高墩大跨连续刚构桥悬臂施工的预拱度设置,而且控制精度较高。
7 结 语
文中分析了高墩大跨连续刚构桥在悬臂施工过程中影响预拱度设置的主要因素,基于大跨度桥梁施工力学理论体系,对悬臂施工过程正确地进行结构分析,得出了在主要因素作用下梁体挠度的计算公式,为施工过程中预拱度的合理设置提供理论依据,保证成桥线形符合设计要求。最后通过工程实例验证了在施工过程中预拱度设置的合理性。需要指出的是,文中只分析了悬臂施工过程中挠度的控制,但在实际施工过程中应该将应力测试和变形控制相结合,实时测量,合理设置预拱度,确保桥梁的线形和应力达到设计要求。
参考文献:
[1]姚玲森.桥梁工程(第二版)[M].北京:人民交通出版社,2010.
[2]徐君兰.大跨度桥梁施工控制[M].北京:人民交通出版社,2000.
[3]陈守辉.大跨度预应力混凝土连续梁桥收缩徐变效应分析[J].铁道建筑,2009,(8):15-17.
[4]肖勇刚,陈海兵,胡斯亮.混凝土连续梁施工过程中的温度效应分析[J].中外公路,2008,28(2):107-109.
[5]贺拴海.桥梁结构理论与计算方法[M].北京:人民交通出版社,2003.
[6]孙训方,方孝淑,关来泰.材料力学(1)(第四版)[M].北京:高等教育出版社,2009.
[7]刘红霞.共轭梁法在梁变形中的应用[J].长沙大学学报,2002,16(2):63-66.
[8]周威,郑文忠.预应力等效荷载计算的通用方法及简化[J].哈尔滨工业大学学报,2005,37(1):49-51,83.
[9]范立础.桥梁工程(第二版)[M].北京:人民交通出版社,2001.
[10]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2001.
[11]朱果.大跨度预应力混凝土连续箱梁桥收缩徐变效应分析[D].重庆:重庆交通大学,2012.
[12]朱中华.大跨度连续刚构桥日照温度效应研究[D].湖南:长沙理工大学,2011.
[13]严露.高墩大跨连续刚构桥温度效应分析与工程控制[D].湖南:长沙理工大学,2007.
[14]包世华.结构力学(上)(第三版)[M].武汉:武汉理工大学出版社,2010.
[15]李小胜,李小鹏.利用虚功原理计算T构悬臂端日照温差位移的方法[J].石河子大学学报,2010,28(6):775-780.
TheResearchofPrestressingCamberSettingintheCantileverConstructionProcessofLong-spanContinualRidgeFrameBridgeswithHighPiers
CHENG Zhong-peng1,JIA Bin1,CHEN Biao2
(1.SchoolofCivilEngineering,LanzhouJiaotongUniversity,Lanzhou,Gansu730070,China;2.XinjiangRailwaySurveyandDesignBranchofChinaRailwayFirstSurveyandDesignInstituteGroupCo.,Ltd.,Urumqi,Xinjiang830011,China)
Abstract:Here,the main factors influencing the bridge deflections were analyzed in construction progress. According to the theoretical calculation method of bridge structure,the deflection calculation formula of bridge was obtained under corresponding loads,and then was applied in the bridge deflection calculation of different construction phases. The construction alignment of the bridge was controlled by setting corresponding prestressing cambers. Finally through the example of practical engineering,the rationality of setting prestressing cambers was validated. This result will provide the theoretical base for setting reasonable prestressing cambers of similar bridge engineerings.
Keywords;bridge engineering;prestressing camber;cantilever construction;the long-span continual ridge frame bridge with high piers
DOI:10.3969/j.issn.1672-1144.2014.05.004
中图分类号:U445.7+2
文献标识码:A
文章编号:1672—1144(2014)05—0018—05
作者简介:成仲鹏(1988—),男,甘肃白银人,硕士研究生,研究方向为桥梁结构设计理论和大跨度桥梁施工控制。
收稿日期:2014-04-16修稿日期:2014-05-11
