基于爆炸超压场重建的传感器优化布局技术研究*

白苗苗,郭亚丽,王黎明

(中北大学信息与通信工程学院,太原 030051)



基于爆炸超压场重建的传感器优化布局技术研究*

白苗苗,郭亚丽,王黎明*

(中北大学信息与通信工程学院,太原 030051)

研究目的是提出一种合理的传感器布局方案,使得利用最少数目的传感器重建出最高精度的爆炸超压场。采用走时层析重建的方法重建爆炸后的超压场,从超压场重建的角度提出了4个指导传感器布局的指标。首先根据爆炸冲击波传输规律建立分区域多尺度网格模型,其次采用遗传算法进行全局搜索,选取满足这4个指标的传感器最优布局方案,最后利用MATLAB进行仿真实验,并对不同传感器布局方式下这4个指标的变化规律及重建精度进行分析和讨论。实验证明,采用本文的传感器布局方案可以在满足重建精度的前提下最大程度地减少传感器数目,进而为实际爆炸试验节省费用。

爆炸超压场;传感器优化布局;遗传算法;走时层析;分区域多尺度

在现代国防军事、国民经济建设、生物医学等领域中,爆炸技术(像水中爆炸、空中爆炸、地下爆炸等)普遍运用,如水雷鱼雷炸毁战船、地震勘探、开山钻井等,爆炸技术得到了较广泛的研究应用。然而爆炸过程反应剧烈、迅速,很难直接测量爆炸后整个波阵面上的超压,目前主要借助于各类传感器进行点测试,以此来估计爆炸的性能和威力。

本文在点测试的基础上,利用走时层析反演技术重建整个波阵面上的超压。一般用于爆炸类实验的传感器制作复杂、费用昂贵,而且爆炸类实验带有破坏性,传感器不能再次利用。因此,出于经济等资源条件限制的考虑,在选择传感器数量上应适宜,同时提出符合实际的指标最优下的传感器优化布站方案是关键[1]。本文研究目的就是给出切合实际的具体优化指标和约束条件、采用合理的优化算法、确定传感器的数目、提出一种合理的传感器布局方案,使得利用较少数目的传感器,重建出较好精度的超压场,最大程度地节省成本提高重建精度。

在传感器的布局研究中,国内外的专家学者做了一定的研究。现今的传感器布局有些是凭借经验布置,有些是通过一定优化方法对传感器数量和位置进行优化设计后进行的[2-3]。然而实验要求不同,传感器布局方式也随之改变。本文从爆炸超压场重建角度提出了4个指导传感器布局的指标,利用遗传算法[4-5]选取合适数目的传感器及满足所提出的4个指标的最优化布局。建立分区域多尺度模型,利用MATLAB进行仿真实验分析,并得出结论。

1 超压场重建整体方案

本文采用走时层析的方法[6-7]重建水中爆炸超压场,即在中心炸点周围布放M个传感器,爆炸后冲击波从中心炸点到传感器形成M条传播路径射线;根据冲击波的传输规律,将所要重建的区域根据爆炸后冲击波的衰减传输规律,划分为N个指数离散网格单元,如图1所示。

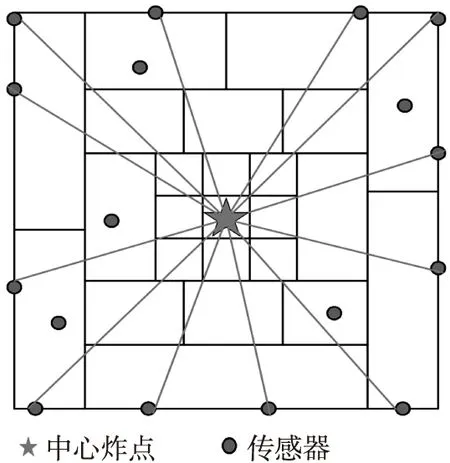
图1 区域模型假设及传感器分布

冲击波在传输的过程中,冲击波的走时即从中心炸点传播到传感器的时间的是速度v(x,y)和几何路径L的函数。对于第i条射线,若射线的走时为ti,则有下列积分:

(1)

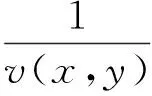
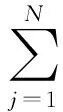
(2)

即

DS=T

(3)

式中,ti:第i条射线的走时;dij:第i条射线穿过第j个网格的射线长度;sj:第j个网格中的慢度;M:射线数;N:网格数。其中,T=(t1,t2…tm)′为各冲击波从炸点中心传至传感器的时间,即冲击波走时,为M维列向量;S=(s1,s2…sn)′为冲击波在每个离散单元传播速度的倒数,即慢度值,为N维未知的列向量;D为M×N阶距离矩阵,其元素为dij,表示冲击波在每个网格单元内的欧几里得距离。

观察方程(3)可知,冲击波路径矩阵D的结构直接影响着重建的好坏,而D又取决于反演区域的离散模型和测试传感器的布局。因此,试验设计可以通过改善网格模型和优化传感器分布,从而改善矩阵D的结构。本文根据实际的实验场景,对待重建区域建立合适的网格模型,利用遗传算法寻找该模型下传感器的最优布局,改善距离矩阵D结构,提高重建精度,选择出最少传感器数目及最优的布局模式,指导实际试验。

2 传感器布局优化指标

2.1 特征值和秩对改善矩阵的作用

从矩阵的角度出发求解方程(3)就是求系数矩阵D的逆矩阵,但是在这种单一爆炸源的爆炸层析成像中,系数矩阵D一般是奇异矩阵,不存在通常意义下的逆矩阵,因此需要采用广义逆理论进行求解。对距离矩阵D∈RM×N进行奇异值分解得:

D=U∑VT

(4)

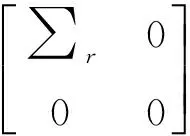
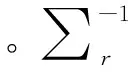
由此,将矩阵D的奇异值和秩作为评价反演问题稳定性的主要指标,故定义评价函数:

(5)

λ1为DTD的最大特征值;λi为DTD的所有特征值,P为矩阵D的秩。E由两部分组成,第一部分反映了D中奇异值的相对分布情况,第二部分反映了D中零空间的相对大小情况。E越大,矩阵D的数学性质越好,反演结果也越稳定可靠[8-10]。

2.2 条件数对改善方程稳定性的作用

单一爆炸源的爆炸场重建问题难点在于求解欠定方程组(3),其解的稳定性由方程(3)中系数矩阵D的条件数决定,条件数越大,问题的稳定性越差,反之亦然[11]。

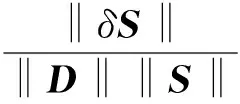
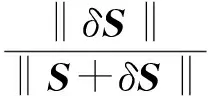
(6)

可见当系数矩阵D带有误差时,方程组解的相对误差仍然取决于条件数的大小。因此条件数是评价方程组解质量的又一个重要指标,条件数越大,方程组的病态程度越大。

2.3 射线密度和射线正交性

射线密度表示通过各网格像元的射线数目,使得方程组的解存在零空间的主要因素是那些没有射线穿过的网格单元,增大射线密度也就是增大矩阵D的非零元素的个数,避免矩阵D的某个列向量等于零向量;射线正交性是通过各网格像元的射线之间最大夹角的余弦值来度量,射线正交性越小,就越容易引起矩阵D的行向量线性相关。

本文中网格单元射线密度的定义用每个单元网格的射线长度总和除以该网格单元的面积,即

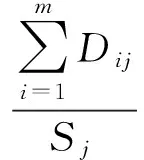
(7)

其中,Mj表示每个网格单元的密度;m表示射线总条数;n表示网格总数;Sj表示网格单元面积。

网格单元射线正交性定义为穿过改网格单元的所有射线最大夹角的正弦值,即

Oj=sin(max(θ)),j=1,2,…,n

(8)

其中,Oj表示射线正交性;θ表示每个网格单元内穿过的所有射线的夹角。

射线密度小和正交性差的区域,反演误差大;反之,则结果比较可靠。在射线总数一定时,根据测试区域的现状,模型分布特点等合理分布射线[12]。

传感器布设时,应使射线覆盖面广、分布均匀、减少射线路径矩阵中零元素的个数、降低其条件数。为了使重建区域内布设的传感器尽可能多方位覆盖被测区域,根据有效的射线总数和重建区域的大小以及射线密度等因素,对传感器进行合理布局。

3 模型试验

3.1 模型建立及试验方法

本文所提出的传感器布局方案适用于水中爆炸、空中爆炸、地下爆炸等,根据装药量的大小以及具体的实验场景选择不同的参数及网格策略,但这4个指标通用,适用于任何试验场景的爆炸超压场重建。

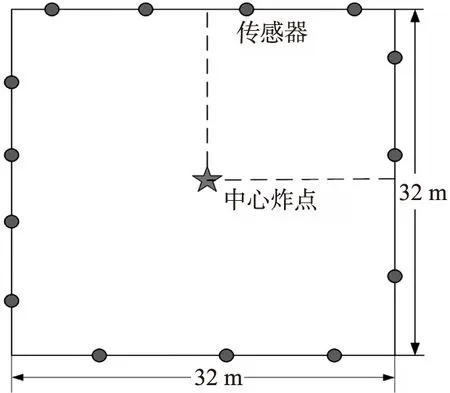
图2 爆炸场模型

下面建立一个正方形区域的爆炸场模型进行试验仿真分析,如图2所示,一个32 m×32 m的理想正方形爆炸区域,炸点位于区域中心,区域边界上放置一定数目的传感器。爆炸后,冲击波从中心炸点传播至传感器,通过对冲击波信号进行处理提取冲击波从中心炸点到达传感器的冲击波走时。利用本文走时层析重建方法重建出整个正方形区域内的二维爆炸速度场,再根据速度和超压的物理关系将速度换算成超压。根据理想爆炸对称近似性,为了试验方便,仿真实验分析只取90°方向的范围重建。利用库尔经验公式求取每个网格的速度值作为实验的真实值,与试验重建所得的每个网格速度值作比较,分析重建精度。

试验步骤如下:

第1步,按照冲击波衰减规律,将该32 m×32 m正方形爆炸区域划分成一定分辨率的小网格。

第2步,结合第2节提出的4个传感器布局指标,利用遗传算法进行全局搜索,找到最少数目的传感器及最佳的布局方式。

第3步,在保证重建的基础上,在重建区域内部放置适当数目的传感器,作为先验信息,一则提高重建精度,二则为了增加重建迭代的收敛速度[15]。

3.2 网格划分策略

重建区域模型划分策略直接影响着传感器的优化布局。在重建区域模型策略方面,我们要充分考虑系数矩阵D的线性相关性,选取合适的重建模型策略[13-14]。

如图3所示,同样布局的6个传感器,如要按照图3(a)的矩形网格划分,只可以建立3个有效方程组,因为该网格划分使得上下传感器分布射线线性相关,若换成图3(b)的划分方式,则可建立6个方程组。如图4所示的同心圆模型,图4(a)模型建立的方程组近似线性相关,而图4(b)使得D互不相关,减小了解的不确定性。如图5(a)所示,规则的4×4网格模型,四条射线穿过网格距离相等,会导致D近似线性相关,若变成图5(b)的不规则网格,可以降低其相关性。

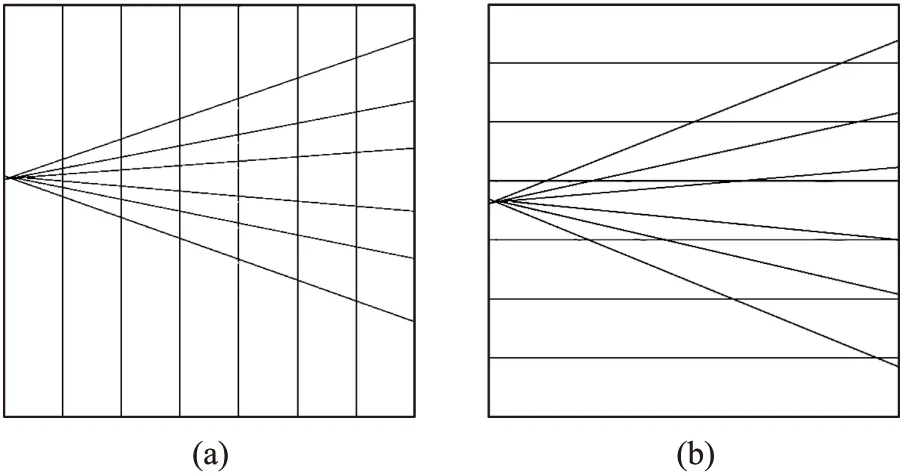
图3

本文的网格划分根据冲击波的传播规律,采用分区域多尺度网格模型,如图6所示。首先,根据爆炸冲击波的衰减规律,我们将待重建的90°方向区域划分为近场、次近场、中场、远场4个区域;其次,对每个子区域分别进行间距不等的不规则矩形网格划分。本模型中将该90°区域划分为58个分辨率不同的网格单元。以爆炸点到每个网格中心的几何距离为爆心距,利用库尔经验公式求取每个网格的速度值作为实验真值。

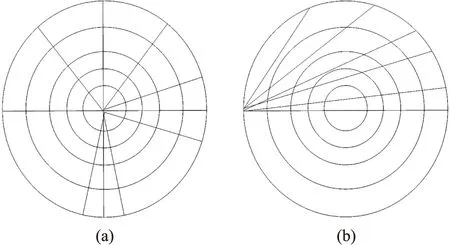
图4

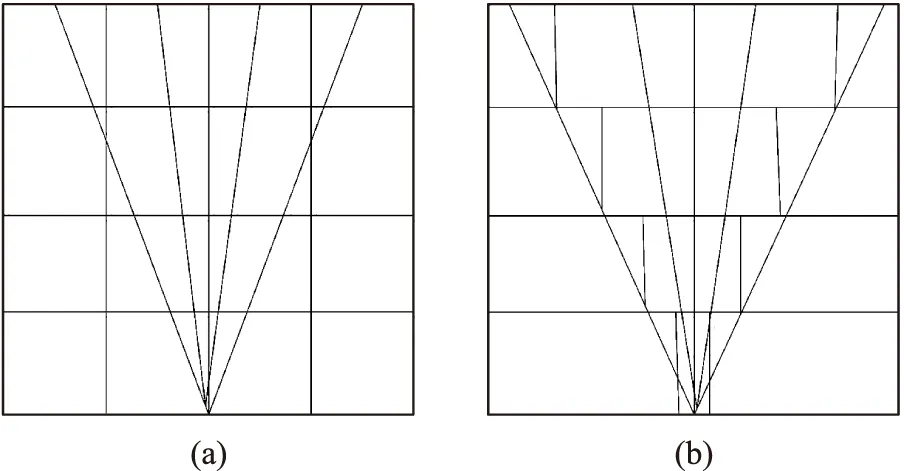
图5

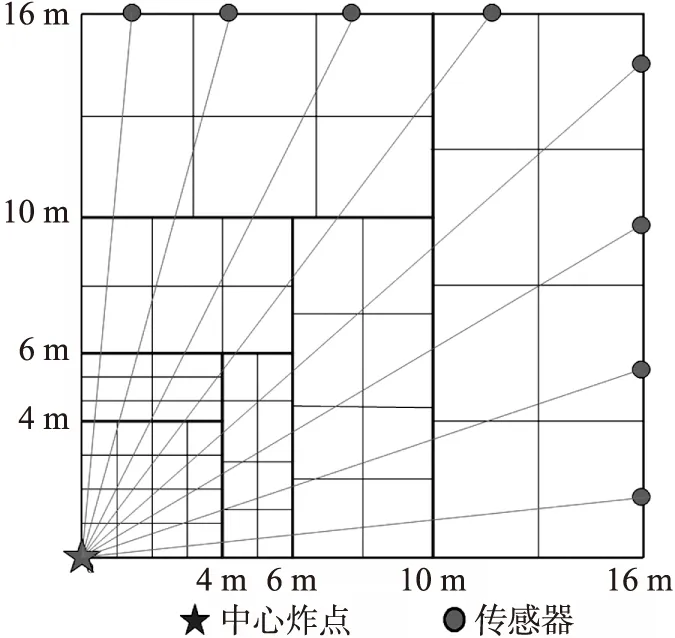
图6 本文分区域多尺度模型

3.3 仿真试验结果

3.3.1 传感器尽量满秩分布

结合以上模型,传感器的布局首先要保证每个网格内均有射线穿过,使得问题可解,在此基础上调节传感器的位置来改善方程(3)的性态。下面固定传感器数目为13个,任意变化其位置求得不同布局下系数矩阵,从上文提出的指标E1,E2,矩阵特征值,射线正交性,密射线度,重建误差方面展开分析,观察不同传感器布局与这些指标之间的规律。

由图7可知,在13个传感器满秩分布下,即P=13时,系数矩阵DDT特征值为个数13个,当这13个传感器不满秩分布时,其特征值个数小于13个,而且每个特征值都比满秩分布的特征值大;由图3可知,随着秩的不断减小,他们的特征值曲线依次降低,说明特征值依次降低,特征值数目依次减少。

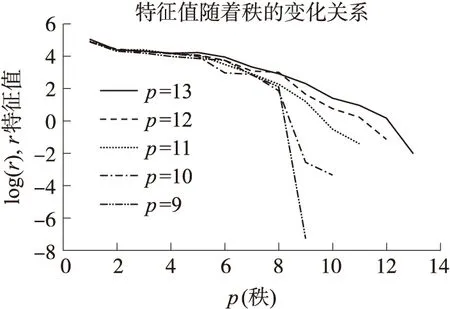
图7 同一数目的传感器不同布局下特征值的变化情况

观察表1中其他指标的变化,可以看到随着秩的减小,指标E(D)也依次减小,说明D的数学性质变差,同时D的条件数急剧增大,满秩时条件数是34.396 6,不满秩时条件数为e+015次方数量级,说明方程变得越来越不稳定;满秩分布的射线密度比不满秩大,说明满秩分布时射线覆盖范围广,而射线正交性基本不变;从重建结果看,不满秩分布的重建误差比满秩分布的误差大。

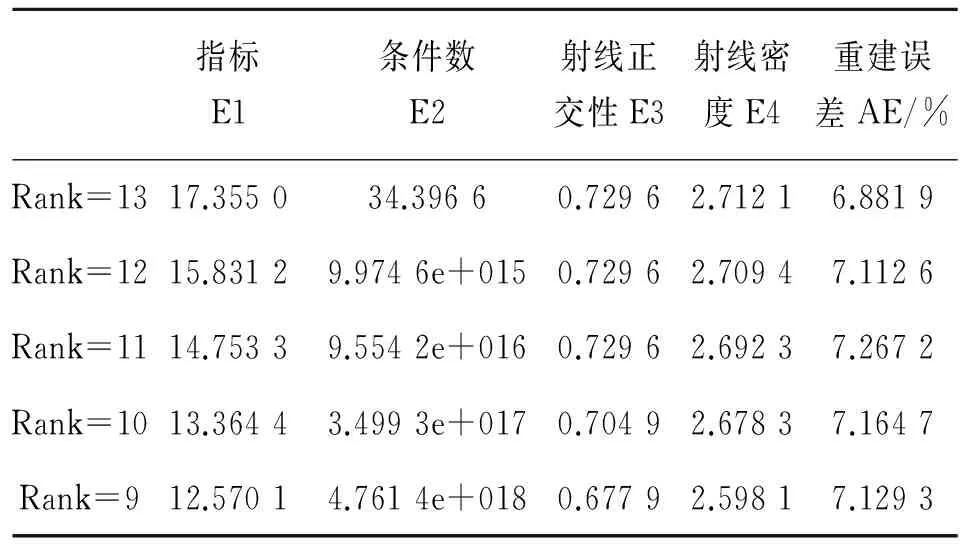
表1 相同数目的传感器在不同布局下各指标的变化规律

综上所述,在传感器数目一定的条件下,调整传感器的布局,使得系数矩阵D满秩分布,这样可以降低方程条件数,提高射线密度,使得方程解比较稳定,从而提高重建精度。

3.3.2 极大线性无关组调整传感器位置

向量组的极大线性无关组是不唯一的,但其极大线性无关组中所含向量的个数是唯一的。由于矩阵的秩就是该矩阵的行向量组或列向量组的极大线性无关组所含向量的个数,所以可以用向量组的极大线性无关组来确定一些矩阵秩的范围。正是由于向量组的极大线性无关组与秩的这种联系,使得在解决向量组的秩的问题中常常要“借用”极大线性无关组。

本文对系数矩阵D的转置矩阵DT做初等行变换,变成阶梯型矩阵,观察阶梯矩阵的每个阶梯子式,调节相应的传感器位置,使得D满秩。如图8(a)所示的13个传感器分布,解算求得其系数矩阵D的秩为12,说明该布局中某两个传感器位置导致所构成的两行元素是线性相关的,利用MATLAB函数命令对DT做初等行变化,得到阶梯矩阵,发现该阶梯矩阵的第一第二行在同一阶梯上,说明1号和2号传感器位置不当导致了不满秩分布,观察这两个传感器的布局,发现它们穿过的同样编号的网格,从而导致了其线性相关。调整其中一个的位置,消除线性相关,调整后如图8(b)所示,调整后的系数矩阵D满秩分布。

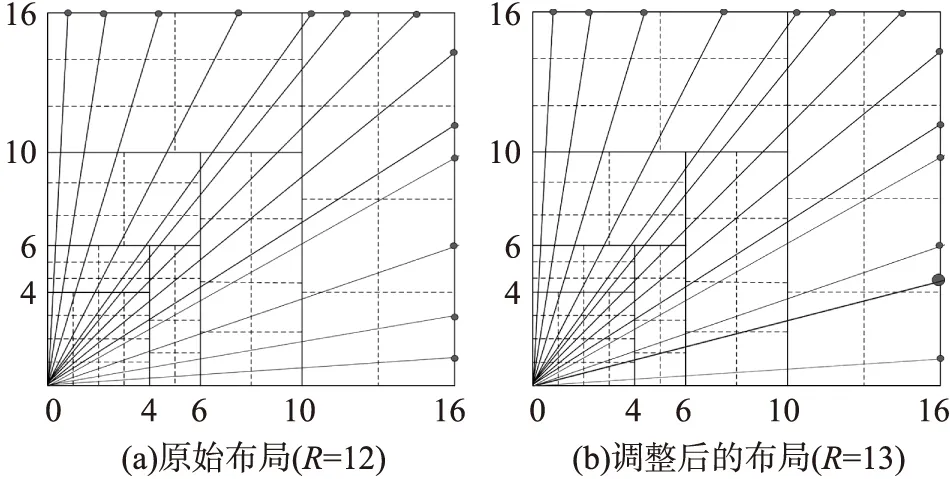
图8

3.3.3 优化布局对传感器数目的要求

研究传感器优化布局的目的就是尽可能利用少量数目的传感器重建爆炸场,下面在遗传算法的基础上依次减少传感器的数目,观察重建结果。结合第3节中所给的指标,建立合适的目标函数,利用遗传算法求得一定数目的传感器满足评价指标的最优布局,即利用遗传算法,使得每一组传感器布局尽量满足E(D)较大,条件数较小,密度较大,正交性好这几个指标。

下面将传感器数目从13个依次减少至5个,直到遗传算法不能寻找出更少数目的传感器来重建该模型。结果如下:

图9显示了不同传感器数目下,矩阵DDT的特征值分布,每组传感器均满秩分布。我们可以看出,13个传感的特征值曲线位于最上面,而且曲线最长,随着传感器数目的减少,各特征值曲线降低且变短,这一变化趋势说明传感器多,特征值数值大并且数目多,方程病态程度较小,解比较稳定。

观察表2可知,可以看到随着传感器数目的减少,指标E(D)也依次减小,说明D的数学性质变差;同时D的条件数爷减少;射线密度逐渐变小,说明传感器越多,射线覆盖范围越广,而射线正交性基本不变;从重建结果看,传感器越少,重建误差越大,重建结果越不好。当传感器数目为13个时,重建误差为6.8768%,当传感器数目减少到5个时,重建误差为7.794 6%。可见,重建精度很大程度上依赖于传感器的个数,所以,实际试验中若要节省费用,就以牺牲重建精度为代价,减少传感器数目;若要达到高精度重建,就需要增加传感器数目。

图9 不同传感器数目下特征值的分布

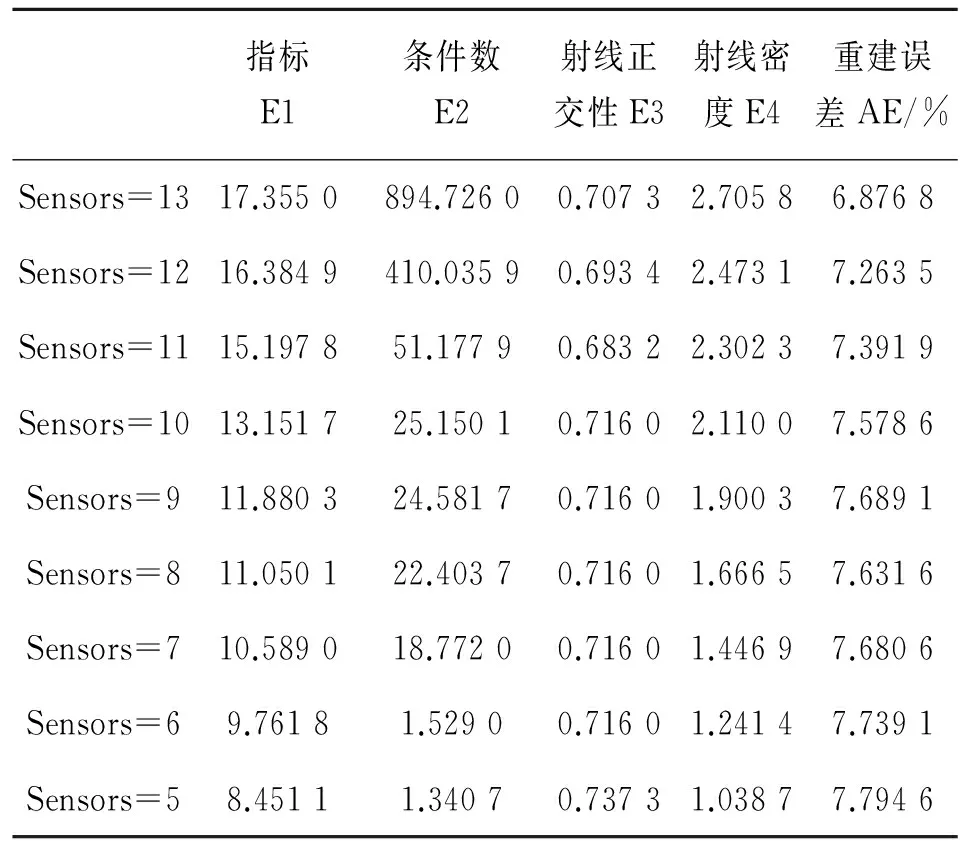
表2 不同数目的传感器最优布局下各指标的变化规律

3.3.4 全部区域重建结果

通过以上分析,重建整个32 m×32 m正方形区域。要求所需要的传感器数目不超过30个,重建平均误差AE<7%,步骤如下:

第1步,按照冲击波衰减规律,将正方形爆炸区域划分近场、次近场、中场、远场4个子区域,对每个子区域采用不同尺度的网格划分策略,如图10所示,将整个区域划分为大小不同的264个网格单元。

第2步,结合以上4个传感器布局指标,利用遗传算法进行全局搜索,找到最少数目的传感器及最佳的布局方式,如图10所示,至少需要24个传感器来重建该区域的速度场。

第3步,将剩余的6个传感器放置在区域边界内如图10所示,让它们遍布在4个区域,将这6个位置的测得的数据作为先验信息,加入重建算法提高重建精度。

重建结果分析如下:这种优化布局模式下,重建结果的平均误差AE=6.698 1%,此时指标E1=33.349 6,指标E2=9.702 0,由于传感器数目比较少,每个网格几乎只有一条射线穿过,所以每个网格单元的射线正交性基本一样,射线密度如图11所示。

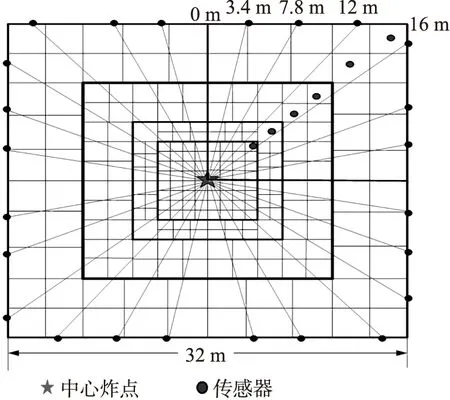
图10 完全爆炸场重建传感器布局

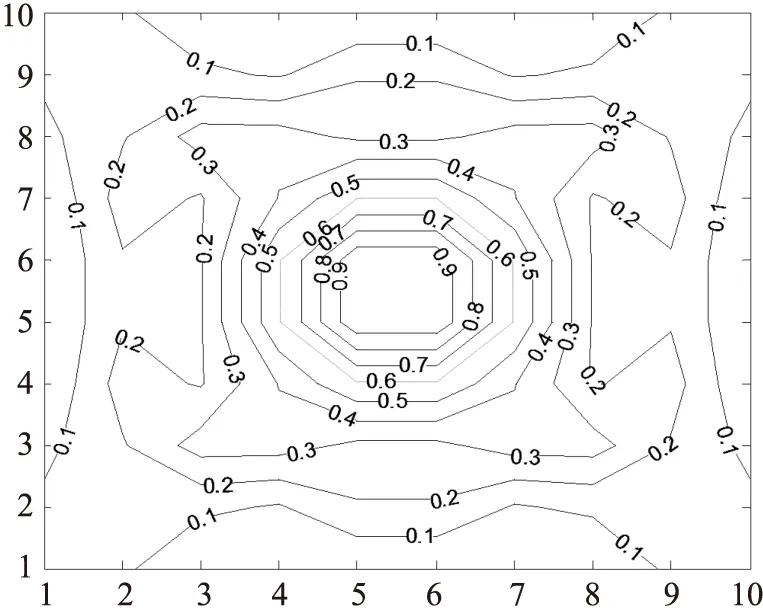
图11 射线密度分布曲线

4 结论

首先,本文提出了一种爆炸超压场重建的方案,基于这种方案,我们对待重建爆炸场进行分区域多尺度网格划分策略。其次,本文从爆炸场重建方面研究探讨,提出了4种指导传感器优化布局的指标,并给出了优化布局方案。得出以下结论:

①分区域多尺度网格划分策略可以满足近场、中场、远场的不同分辨率要求,抗干扰能力强,节省传感器。

②传感器布局时,尽量使得射线路径矩阵的秩越大越好、特征值越大越好、射线密度越大越好、射线正交性越大越好、条件数越小越好。

③同样数目的传感器布局时,尽量使射线路径矩阵满秩分布,这样可以降低方程条件数,提高射线密度,使得方程解比较稳定,从而提高重建精度。若不满秩分布,可以根据射线路径矩阵的极大线性无关性对传感器位置微调,使其达到最优。

④重建精度很大程度上依赖于传感器的个数,我们利用本文指导方案,使得重建边界传感器达到饱和,将剩余的的传感器布放在区域内部作为先验信息提高重建精度。

⑤在实际实验测试中,我们可以结合实际情况,利用文中所提出的4个指标建立合适的适应度函数,利用遗传算法,寻找最少数目的传感器、最优化的布局模式,指导野外施工,节省实验成本。

[1] 刘艳,刘贵杰,刘波.传感器优化布置研究现状与展望[J].传感器与微系统,2010,11(29):4-6.

[2]李石坚,廖备水,吴健.面向目标跟踪的传感器网络设计、实现和布局优化[J].传感技术学报,2007,12(20):2622-2630.

[3]黄亚东,张土乔,宋洁人.考虑可靠性的给水管网水质传感器多目标优化选址模型[J].传感技术学报,2007,8(20):1888-1893.

[4]汤可宗.遗传算法与粒子群优化算法的改进及应用研究[D].南京:南京理工大学,2011:8.

[5]Michalewicz Z.Genetic Algorithms Data Structures=Evolution Program[J].Artificial Intelligence,Berlin:Springer,1992:1.

[6]秦宁,李振春,杨晓东.自动拾取的成像空间域走时层析速度反演[J].石油地球物理勘探,2012,47(3):392-398.

[7]刘国华,王振宇,孙坚.弹性波层析成像及其在土木工程中的应用[J].土木工程学报,2003,36(5):76-81.

[8]Wéber Z.Optimizing Model Parameterization in 2D Linearized Seismic Traveltime Tomography[J].Physics of the Earth and Planetary Interiors,2001,124(1):33-43.

[9]Curtis A,Snieder R.Reconditioning Inverse Problems Using the Genetic Algorithm and Revised Parameterization[J].Geophysics,1997,62(5):1524-1532.

[10]Curtis A.Theory of Model-Based Geophysical Survey and Experimental Design:Part 1—Linear Problems[J].The Leading Edge,2004,23(10):997-1004.

[11]成谷.地震反射走时层析理论与应用研究[D].上海:同济大学,2004:6.

[12]Passerini C,Falciasecca G.Modeling of Orthogonality Factor Using Ray-Tracing Predictions[J].IEEE Transactions on Wireless Communications,2004,3(6):2051-2059.

[13]Zhou H.Multiscale Traveltime Tomography[J].Geophysics,2003,68(5):1639-1649.

[14]Vesnaver A.Null Space Reduction in the Linearized Tomographic Inversion[J].Full Field Inversion Methods in Ocean and Seismo-Acoustics.Kluwer Academic Publishers,Dordrecht,1995:139-145.

[15]白苗苗,郭亚丽,王黎明.基于EM算法的爆炸超压场重建技术研究[J].弹箭与制导学报,录用待发表.

白苗苗(1987-),女,甘肃庆阳人,研究生在读。研究方向为信号与信息处理、爆炸场重建、反演算法,baimiaomiao641@163.com;

王黎明(1974-),男,教授,博士生导师,主要从事X射线图像处理、多维信号获取与处理、无损检测技术等领域的教学和研究工作,wlm@nuc.edu.cn。

StudyonOptimalSensorPlacementMethodBasedontheReconstructionofExplosionOverpressureField*

BAIMiaomiao,GuoYali,WANGLiming*

(College of Communication and Information Technology,North University of China,Taiyuan 030051,China)

The chief aim of the study is to propose a reasonable sensor placement method in order to reconstruct explosion overpressure field at the highest precision by a minimum number of sensors.Tomographic methods is adopted to reconstruct overpressure field of shock wave induced by explosion.The article put forward four measurement indexes for sensor deployment from the aspect of the reconstruction of explosion overpressure field.First,a multi-scale reconstruction model for explosion field in subregions was established according to the propagation law of shock wave.Then,the genetic algorithm was adopted to conduct global search and optimal sensor layout methods which satisfies the four requirements were selected.Finally,the paper analyzed the variation and precision of these four indexes in different sensor placements according to the MATLAB simulation experiments.Results indicated that the sensor placement method proposed by the paper can reach high reconstruction accuracy with the utmost reduction of the number of sensors which will guide real explosion experiments to a cost-effective way.

explosion overpressure field;optimal sensor placement;Genetic Algorithms;travel time tomography;Subregional multi-scale

项目来源:山西省自然科学基金项目(2013011017-8);山西省回国留学人员科研项目(2013-083);高等学校博士学科点专项科研基金项目(博导类)(20121420110006)

2014-04-14修改日期:2014-05-26

10.3969/j.issn.1004-1699.2014.07.007

TP301.6

:A

:1004-1699(2014)07-0886-07