MEMS圆盘谐振器形变对电气刚度影响分析*

董林玺,俞 权,包金艳,陶家平

(1.杭州电子科技大学射频电路与系统教育部重点实验室,杭州 310018;2.中科院上海传感技术联合国家重点实验室,上海 200050)



MEMS圆盘谐振器形变对电气刚度影响分析*

董林玺1,2*,俞 权1,包金艳1,陶家平1

(1.杭州电子科技大学射频电路与系统教育部重点实验室,杭州 310018;2.中科院上海传感技术联合国家重点实验室,上海 200050)

电气刚度是影响MEMS谐振器谐振频率精度的因素之一。但是对于谐振器受到应力时,产生的形变量对电气刚度的影响的理论研究报道甚少。鉴于此,本文对电容式盘结构谐振器受径向静电力和纵向惯性力下的形变量以及电气刚度的改变量进行了系统的理论分析。研究结果表明,当圆盘与电极间隙为50 nm,且电压达到50 V时,圆盘由于静电力产生的径向形变量可达间隙的2.05%,电气刚度改变6.15%。当圆盘半径为100 μm,且受到10 000gn的纵向惯性力时,其最大形变量可以达到圆盘厚度的2.4%,电气刚度改变2.4%。本文分析结果对其他盘结构谐振器的分析亦有重要借鉴意义。

MEMS圆盘谐振器;静电力;惯性力;形变量;电气刚度

微机电系统MEMS(Micro Electro Mechanical Systems),是微电子技术的拓宽和延伸,它是将微电子技术和精密机械加工技术相互融合,并将微电子与机械融为一体的系统。MEMS现已成为全世界增长最快的市场之一,不断开拓汽车、医学、航天和军事市场[1-2]。而对于MEMS器件的研究是提高其性能的关键因素。在MEMS器件中,圆盘谐振器由于其频率高,集成度高,Q值高,功耗小等优势成为学者研究的热点之一,广泛应用于振荡器、滤波器等无线通信系统的元件中[3-4]。

在对圆盘谐振器的研究中,电气刚度引起的静电弹簧软化效应能使圆盘谐振频率发生微小频偏。因此,研究电气刚度对提高谐振频率精度,提升谐振器性能尤为重要。Clark T C Nguyen研究了电气刚度产生原理并分析了它对圆盘谐振器谐振频率偏移的影响[5]。Mehmet Akgul研究了圆盘谐振器阵列的电气刚度调谐机制来提高阵列输出电流[6]。但是他们研究电气刚度时,没有考虑到圆盘受外界应力时,产生的形变会导致电气刚度发生变化。鉴于此,本文分析了圆盘谐振器受静电力和外界惯性力时,产生的形变量对电气刚度大小的影响。

1 圆盘谐振器运行原理

中心支撑径向模式圆盘谐振器原理图如图1所示。

图1 中心支撑径向模式圆盘谐振器原理图

圆盘谐振器及电极由多晶硅制成。圆盘通过底面圆柱形锚悬空在基片上,两边电极包围其圆盘,并通过狭小的间隙(通常为真空)形成电容式换能器[7-8]。当圆盘本身加载直流偏置电压V,输入电极加载与圆盘一阶固有频率相同的交流小信号电压vi时,圆盘与电极之间产生发射状时变静电力,使圆盘径向扩大和缩小。静电力大小可以表示为[9]

(1)

其中C为圆盘与输入电极电容,r为圆盘径向形变。圆盘的这种谐振运动使输出电极端产生了时变电容,进而在输出电极产生交流输出电流。由于静电弹簧软化效应,圆盘振动时的谐振频率小于其固有频率,其大小可以表示为[10]

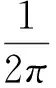
(2)

其中f0为谐振频率,f为固有频率,mre为圆盘有效质量,km为纯机械刚度,ke为电气刚度,其大小可以表示为

(3)

其中ε0为真空介电常数,A为圆盘与电极重叠面积,d为圆盘与电极初始间隙,R为圆盘半径,t为圆盘厚度。当圆盘的纯机械刚度和有效质量不变时,电气刚度的变化决定了圆盘谐振频率精度。

2 径向静电力下形变及电气刚度分析

当圆盘加载直流偏置电压时,产生的固定静电力分量能使圆盘产生一定的径向形变。此形变会导致检测电容产生一定变化,从而改变电气刚度大小。根据式(1)可得,其右边第一部分静电力分量与交流小信号电压频率相同,使圆盘发生谐振运动。第二部分为固定静电力分量,使圆盘发生径向固定形变。而输出电极与圆盘之间也有固定的静电力分量,大小与输入电极和圆盘之间的静电力相等。由于输入输出电极几乎完全包围圆盘,因此可以认为圆盘横截面每个节点受到相等的固定静电力。圆盘受径向静电力示意图如图2所示。

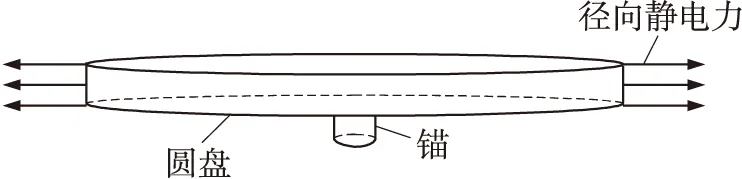
图2 圆盘受径向静电力示意图

现分析圆盘由于固定静电力而产生的径向形变量。由弹性力学的知识以及广义胡克定律可得,当圆盘的半径为R,杨氏模量为E,泊松比为υ,横截面受均匀应力P时,其平衡方程可以简化为[11]

(4)

其中u为径向形变大小,r为圆盘某节点离圆盘中心的距离。方程边界条件为圆盘中心和边界的应力载荷,即当r=0时,应力σr=0,当r=R时,σr=P。通过广义胡克定律中应力应变关系,可以得到其解为

(5)

对于MEMS圆盘谐振器,其驱动力为静电力,忽略边缘效应,其大小为

(6)

当静电力作用于圆盘时,由于圆盘横截面每个节点所受静电力相等,因此,其应力P值大小为

(7)

在圆盘半径处(r=R),圆盘的形变量可以表示为

(8)

由式(8)可以得到,圆盘横截面上的径向形变量与所加偏置电压的平方成正比,与初始间隙的平方成反比,并与圆盘半径、材料特性有关,与圆盘厚度无关。此形变量将导致圆盘与电极初始间隙发生变化,从而改变了电气刚度大小。其改变幅度可由ke对d的一阶导数得到。

(9)

(10)

由式(10)可得,电气刚度的改变量是圆盘与电极间隙改变量的3倍。以下通过ANSYS仿真分析圆盘在径向静电力下的形变量,并由此计算电气刚度改变量。表1列出了仿真的圆盘材料特性及尺寸。

表1 圆盘谐振器材料特性及尺寸

现分析圆盘固定尺寸下径向形变量与所加电压的关系。根据式(8),可得圆盘边界形变量与电压之间的关系为

通过有限元仿真可得在不同电压下圆盘边界的形变量,将仿真值与理论值进行对比,其结果如图3所示。

图3 理论值与仿真值形变量分析

上述仿真结果是以圆盘右边界的节点x方向的形变值作为参考的,其y方向和z方向的形变量由于比较小,忽略不计。从上图结果可知,理论值和仿真值十分得吻合,误差很小。

实际上,由于器件的非理想性,理论分析与实际器件的运行有一定的不同:理论分析是基于电极完全包围圆盘,圆盘横截面所有节点受力相同而得出的。但是实际中,由于电极不能完全包围圆盘(除非圆盘运行在单端模式,圆盘本身进行信号输出),导致圆盘横截面静电力分布不均匀,使圆盘不能理想化地以径向方向形变。当电压为16 V时,圆盘径向形变分布图如图4所示。

图4 圆盘径向形变分布图

在分析提高圆盘谐振器性能时,可以通过降低间隙和增加偏置电压来降低运动电阻[12-13]。但这也会产生较大的径向形变量,导致电气刚度的改变不能忽略。由上述理论计算,当间隙降为50 nm,偏置电压为50 V时,其形变量能达到间隙的2.05%,电气刚度改变6.15%。此时,电气刚度的改变量对于谐振频率的影响不能忽略。

3 纵向惯性力下形变及电气刚度分析

圆盘谐振器不仅会在工作时由于静电力产生径向形变,而且会由于长期处于惯性条件下而产生形变[14-15],从而改变圆盘谐振器的电气刚度。本文根据圆盘薄板弯曲理论,研究了圆盘纵向形变量与所加静态纵向惯性加速度的关系,并以此分析电气刚度的改变量。

圆盘薄板弯曲的微分方程可以表示为[16]

D22u=q

(11)

2=++

(12)

D称为薄板的弯曲刚度,其大小可以表示为

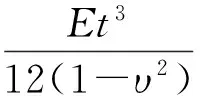
(13)

u为板的纵向弯曲形变量,q为外界纵向静态惯性载荷。圆盘受纵向惯性载荷简图如图5所示。

图5 圆盘受纵向惯性载荷简图

由于此次分析的惯性载荷关于圆盘圆面轴对称,且载荷为静力载荷,因此u与θ无关。此时微分方程可以表示为

(14)

根据圆盘锚点和边界条件,可以计算其解为

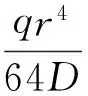
(15)

当r=R时,圆盘的形变量最大,其值可以表示为

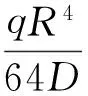
(16)

对于添加的惯性载荷,大小可以表示为F=ma,其中m为圆盘质量,其大小为m=ρAt,其中ρ为圆盘密度。因此,q可以表示为

(17)

将式(13)和式(17)代入式(16),可得

(18)

由式(18)可以得到,圆盘最大纵向形变量与圆盘厚度,圆盘半径,以及材料特性有关,并与所加惯性加速度成线性正比例关系。此形变量将导致圆盘与电极重叠面积发生变化,从而改变了电气刚度大小。其改变幅度可由ke对A的一阶导数得到。

(19)

(20)

由式(20)可得,电气刚度的改变量和圆盘与电极重叠面积改变量相等。以下通过ANSYS仿真分析圆盘在纵向惯性力下的形变量,并由此计算电气刚度改变量。ANSYS可模拟静态惯性加速度,当a=g时,其圆盘纵向形变分布图如图6所示。

图6 圆盘纵向形变分布图

根据表1中材料特性及尺寸,可得圆盘在纵向静态惯性加速度下的最大形变量为

1.75×10-14a

对圆盘施加不同大小的惯性加速度载荷,可以得到圆盘边界不同的最大形变值。把仿真值与理论值进行对比,可得如图7中的关系曲线。

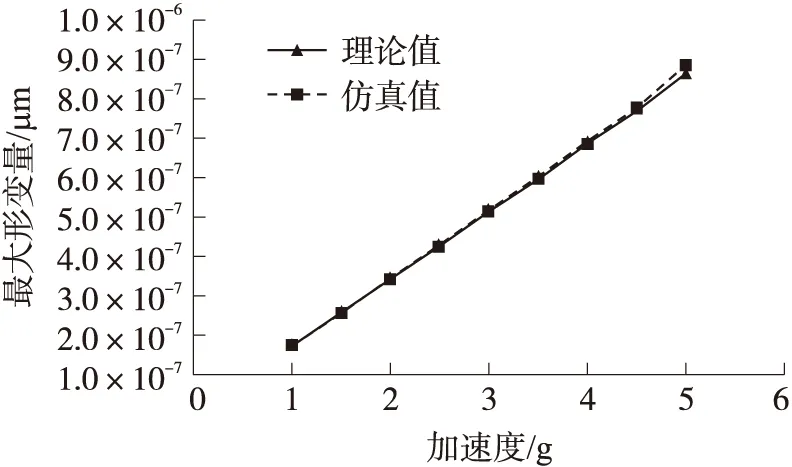
图7 理论值与仿真值的形变量比较

由上述理论分析及仿真结果可得,圆盘最大的形变量发生在圆盘边界,其值与所加的惯性加速度成线性正比例关系。此形变量将使圆盘与电极重叠面积发生变化,导致电气刚度同等程度改变。由上述分析可以得到,当圆盘半径变为100 μm且受到10 000gn的惯性加速度时,圆盘最大形变量为圆盘厚度的2.4%,电气刚度改变2.4%。此时,分析圆盘谐振器谐振频率时此电气刚度改变量需考虑在内。

上述分析是基于圆盘的锚点是无穷小的不动点的假设得到的。实际器件中,锚的有限尺寸会对圆盘的弯曲形变量产生重要影响。图8显示了当a=g时,圆盘边界形变量与锚半径之间的关系曲线。此图表明,增大锚的半径可以显著降低圆盘向下弯曲形变量,从而减小电气刚度的改变。但是增大锚半径会增加从圆盘到基片的能量损耗,从而降低Q值[17]。因此,在设计锚的尺寸时需同时考虑对形变量和Q值的影响。

图8 圆盘边界形变量与锚半径的关系曲线

4 静电力和惯性力同时作用下的电气刚度分析

当径向静电力和纵向惯性力同时作用于圆盘谐振器时,若忽略静电力与惯性力之间的相互作用,电气刚度的该变量可以表示为

(21)

(22)

(23)

由式(23)以及(20)和(10)可得,谐振器电气刚度的改变量可以表示为由径向静电力和纵向惯性力导致的电气刚度的改变量的线性叠加。此外,式(23)表明纵向惯性力导致的电气刚度的降低可以抵消径向静电力导致的电气刚度增加。在实际谐振频率测量中,当圆盘谐振器处于振动环境时,若所加电压一定,可以得到其谐振频率随着纵向惯性力的增加而增加。当所加惯性力一定时,其谐振频率随着偏置电压的增加而减小。并且由于固定径向静电力的形变作用,其谐振频率减小幅度将越来越大。

5 结论

本文分析了圆盘谐振器受径向静电力和纵向惯性力作用下的形变量,得到了径向形变量与所加电压以及纵向形变量与惯性加速度之间的关系曲线,并以此研究电气刚度的改变大小。当圆盘受到径向静电力时,其边界形变量会随着间隙的降低以及电压的增加而显著增加。当间隙降为50 nm且电压达到50 V时,其径向形变量可以达到间隙的2.05%,电气刚度改变6.15%。当圆盘受到纵向惯性力时,其边界形变量最大,其值与所加惯性加速度成线性正比例关系。对于半径为100 μm的圆盘,当惯性加速度为10 000gn时,其最大形变量可以达到圆盘厚度的2.4%,电气刚度改变2.4%。最后,本文分析了圆盘谐振器同时受到径向静电力和纵向惯性力时的电气刚度改变量,得到了实际测量中圆盘谐振器谐振频率的变化与偏置电压和惯性力大小的关系。由于电气刚度决定了圆盘谐振器谐振频率精度,而圆盘受力下的形变使电气刚度发生变化,因此本文结论可为未来设计高频率精度的电容式盘结构谐振器提供依据。

[1] 亢春梅,曹金名,刘光辉,等.国外MEMS技术的现状及其在军事领域中的应用[J].传感器技术,2002,21(6):4-7.

[2]贾英茜,赵正平,杨拥军,等.电容式RF MEMS谐振器[J].微纳电子技术,2010,47(2):99-104.

[3]孙凤鸣,傅星,朱振宇,等.基于MEMS的微位移传感器及其应用研究[J].传感技术学报,2013,26(2):293-296.

[4]董自强,赵博韬,石国超,等.一种超宽带MEMS开关的研制[J].传感技术学报,2014(3):312-315.

[5]Jing Wang,Ren Z,Nguyen C T C,et al.1.156-GHz Self-Aligned Vibrating Micromechanical Disk Resonator[J].IEEE Transactions on Ultrasonics,Ferroelectrics,and Frequency Control,2004,51(12):1607-1628.

[6]Mehmet Akgul Z R,Clark T C Nguyen.Voltage-Controlled Tuning to Optimize MEMS Resonator Arry-Composite Output Power[C]//Frequency Control and the European Frequency and Time Forum(FCS),2011:1-6.

[7]John R Clark,Wan-Thai Hsu,Mohamed A Abdelmoneum,et al.High-Q UHF Micromechanical Radial-Contour Mode Disk Resonators[J].Journal of Microelectromechanical Systems,2005,14(6):1298-1310.

[8]Abdelmoneum M A,Demieci M U,Nguyen T C.Stemless Wine-Glass-Mode Disk Micromechanical Resonators[C]//Proc of IEEE Int MEMS Conf,2003:698-701.

[9]赵剑,王洪喜,贾建援,等.计及边缘效应的静电驱动微结构静电力计算[J].微纳电子技术,2006,43(2):95-97.

[10]Bongsang Kim,Akgul M,Yang lin,et al.Acceleration Sensitivity of Small-Gap Capacitive Micromechanical Resonator Oscillators[C]//Frequency Control Symposium(FCS),2010:273-278.

[11]杨桂通.弹性力学简明教程[M].清华大学出版社,2006:86-89.

[12]Akgul M,Bongsang Kim.Oscillator Far-From-Carrier Phase Noise Reduction via Nano-Scale Gap Tuning of Micromechanical Resonators[C]//Solid-State Sensors,Actuators and Microsystems Conference,2009:798-801.

[13]Mustafa U Demirci,Clark T C Nguyen.Mechanically Corner-Coupled Square Microresonator Array for Reduced Series Motional Resistance[J].Journal of Microelectromechanical Systems,2006,15(6):1419-1436.[14]Lou Wenzhong,Song Renlong,Liu Yunjian.A Novel Multi-Direction High Shock Reliability Test on MEMS Devices[C]//Proceedings of the 2009 4th IEEE International Conference on Nano/Micro Engineered and Molecular Systems,Shenzhen,IEEE,2009:261-264.[15]崔九征,孙博,冯强,等.强冲击条件下MEMS封装可靠性有限元分析[J].机械工程学报,2011,47(24):177-185.

[16]陈明祥.弹塑性力学[M].科学出版社,2006:130-134.

[17]Li Sheng-Shian,Lin Yu-Wei,Xie Yuan,et al.Micromechanical“hollow-disk”ring resonators[C]//Micro Electro Mechanical Systems,2004.17th IEEE International Conference on.(MEMS).2004:821-824.

董林玺(1976-),男,博士,研究员,硕士生导师,主要从事超高精度MEMS传感技术、RF MEMS器件、NEMS谐振器等方面的研究,已发表SCI/EI收录论文二十余篇,donglinxi@hdu.edu.cn;

俞权(1990-),男,硕士,主要从事MEMS谐振器的研究;1024080438@qq.com。

AnalysisofImpactofDeformationonElectricalStiffnessforMEMSDiskResonator*

DONGLinxi1,2*,YUquan1,BAOJinyan1,TAOJiaping1

(1.The Key Laboratory of RF Circuits and System of Ministry of Education,Hangzhou Dianzi University,Hangzhou 310018,China;2.State Key Laboratory of Transducer Technology,Chinese Academy of Sciences,Shanghai 200050,China)

Electrical stiffness is one of the factors that affect the resonant frequency accuracy of MEMS resonator.But there are few reports on the study of the impact of deformation on the electrical stiffness when the resonator is under the stress.Therefore,the deformation under the radial electrostatic force and longitudinal inertial force,and the variation on the electrical stiffness of capacitive disk resonator are systematically analyzed in this paper.The results show that when the gap between the disk and electrodes is 50 nm,and the voltage reaches 50 V,the radial deformation due to the electrostatic force can be 2.05% of the gap and the electrical stiffness changes 6.15%.When the longitudinal inertial force of 10 000gnis supplied,if the radius of disk is 100 μm,the biggest deformation can be 2.4% of the disk thickness and the electrical stiffness changes 2.4%.The results of this paper also have important references for other disk resonators.

MEMS disk resonator;electrostatic force;inertial force;deformation;electrical stiffness

项目来源:国家自然科学基金项目(60506015);浙江省自然科学基金项目(Y107105);GHz频率机械耦合阵列组合的盘结构电容式微机械谐振器关键技术研究项目(61376117);规模集成振动微机械谐振器的静电调谐技术研究项目(LY13F040004)

2014-02-28修改日期:2014-05-26

10.3969/j.issn.1004-1699.2014.07.006

TP212

:A

:1004-1699(2014)07-0881-05