光栅投影测量系统三维形貌拼接技术研究*

刘常杰,刘 洋,刘 邈,李 斌

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)



光栅投影测量系统三维形貌拼接技术研究*

刘常杰*,刘 洋,刘 邈,李 斌

(天津大学精密测试技术及仪器国家重点实验室,天津 300072)

针对尺寸较大或型面复杂的被测物形貌的测量,提出了一种基于投影仪投射标记点和全局控制点的三维形貌拼接方案。方案充分利用光栅投影测量系统的优势,以拼接相机坐标系为中介,将被测物表面在投影系统视觉传感器坐标系下的多视点云坐标转换到全局坐标系下,实现了将投影系统视觉传感器在不同位置、不同角度的测量数据统一到全局坐标系,完成拼接。该方案避免了人工标记点的粘贴,保持了被测物表面的原有形貌,提高了测量效率,同时克服了基于相邻图像重叠拼接中的误差累积问题。此方案方法操作简单,原理可行,精度可满足要求。实验结果表明:拼接的X,Y,Z坐标均方根误差分别为:0.056 mm、0.023 mm、0.165 mm,测量系统的绝对误差为0.33 mm。

光栅投影测量;形貌拼接;投影标记点;全局控制点

目前,如何准确快速地获取物体表面三维信息是一个重要研究方向,在各种测量方法中,光学技术的应用越来越广泛。作为光学技术的一种,光栅投影三维测量技术优势明显,具有非接触、精度高、可移动、测量效率高和数据空间分辨率高等优点[1]。但是在对于尺寸较大或型面复杂的被测物时,由于视场的限制或被测物体表面互相遮掩等问题的存在,通常不能在同一坐标系下将被测物三维数据一次测出,需要根据被测对象,从不同角度对不同的区域进行分块测量,然后再将测量数据拼接构建成三维数据模型,将测量数据统一到一个总体世界坐标系中[2]。三维形貌拼接是其中的关键技术之一,直接影响测量的精度和速度。

现阶段常用的拼接技术主要为以下4种:①利用辅助精密机械结构获取各次测量时坐标系之间的转换关系[3]。这种方法拼接原理简单,但系统灵活性低、占用空间大、设备成本高。②基于标记点的拼接技术。此方法在被测目标表面粘贴一些人工标记点,利用标志点并结合模式识别的方法,完成整体拼接[4]。此方法拼接精度高、可靠,但不适合软质物体与易损物体的测量,随着被测表面增大标记点增多,自动识别错误会增加,更为重要的是标记点的粘贴破坏了被测表面原有形貌,影响测量的真实性。③拼接软件法。此方法摆脱了对于定位装置的依赖[5],常见的如基于最靠近点的迭代ICP(Iterative Closest Point)算法的自由拼接方法[6]。方法操作简单,但是算法复杂程度高,可靠性不高。现有的自由拼接方法大多基于相邻图像的重叠部分,这将不可避免的引入误差累积的问题,难以得到平滑无缝的结果。④利用如经纬仪[7],激光跟踪仪[8],跟踪相机等精密测量设备跟踪面结构光传感器坐标系,这种方法精度高,但是设备成本很高,同时效率较低,结构光传感器的姿态还会影响精密测量设备的测量,需要控制传感器位姿。

本文充分利用投影测量系统的优势,提出一种不使用粘性标记点,利用投影测量系统投射标记点的方案。方案实施过程中需要使用一系列全局控制点和一个全局拼接相机,将投影系统在不同位置、不同视角测得的三维数据统一到全局测量坐标系下,完成拼接。此方案不依赖人工粘贴标记点,保证了被测物表面不被破坏,测量效率高;对投射标记点进行编码,保证了较高的识别精度;由于拼接相机拍摄位置灵活,所以投影系统传感器姿态不受限制;同时从拼接原理上克服了基于相邻图像重叠拼接中的误差累积问题。

1 光栅投影测量系统简介

光栅投影测量系统主要由DLP投影仪,CCD相机和上位测量控制计算机组成[9]。如图1所示,光栅投影测量系统将调制的光栅条纹投射到被测物表面,通过CCD相机采集一系列图像,经过相关的图像处理算法和三维转换模型,可以得到投射条纹区域的被测物表面的点云数据。为了保证测量精度以及考虑到投影仪每次投射区域的有限性,一次投射所测量的区域不能覆盖被测物所有待测表面。这对于被测物尺寸较大的情况,也就需要多次测量,然后再将测量数据拼接构建成三维数据模型。本文提出了一种投影编码标记点的方案,与传统粘贴标记点的方案相比,此方案具有较高的识别精度,不会对软质物体或易损物体造成损伤,同时被测表面形貌特征不会改变,保证了测量数据的准确性。

图1 投影测量系统结构图

2 基于全局坐标系的三维形貌拼接原理

2.1 测量系统整体坐标系转换关系

基于全局控制点拼接属于基于图像控制点约束拼接的一种,其基本原理是通过引入某种中介,形成测量传感器坐标系和全局坐标系的坐标系转换链,求解该转换链后,便可将每次的测量数据统一到全局坐标系中,实现拼接。

如图2所示,投影系统视觉传感器对被测物的某一部分进行测量,可以得到投射条纹区域在投影系统视觉传感器坐标系下三维点云数据。使用大视场高精度拼接相机对分布在被测物体周围的全局控制点成像,建立全局测量坐标系,同时以拼接相机作为中介,首先建立每一个测量位置下拼接相机坐标系与全局测量坐标系的转换关系矩阵Mc-g;之后在视觉传感器移动到每个位置时建立视觉传感器与拼接相机的转换关系矩阵Mc-g;最后推导出传感器坐标系到全局坐标系关系为Ms-g=Ms-c.Mc-g,便可将不同位置、不同视角测得的三维数据统一到全局测量坐标系下,完成点云数据的拼接。

图2 三维形貌拼接示意图

2.2 拼接相机坐标系到全局坐标系的转换

调整拼接相机的位置,使拼接相机一次同时拍摄至少3个全局控制点。根据近景摄影测量中的角锥体原理有:以摄影中心为顶点的两根构像光线的像方角应与其物方角相等[10]。如图3所示,将以上全局坐标系建立过程中用到的三点分别命名为A、B、C,它们在拼接相机像平面上的对应成像点分别为A′、B′、C′,其像面坐标分别为(X1,Y1),(X2,Y2),(X3,Y3)。全局控制点在全局坐标系下的坐标已经确定,所以其间的关系固定已知,即控制点间的距离AB、AC和BC分别为d1、d2和d3,同时相机的焦距为f。拼接相机摄影中心O与3个像点的距离分别为l1,l2,l3,则有

(1)

图3 拼接相机坐标系到全局坐标系的转换原理图

若OA与OB的夹角θ1、OA与OC的夹角θ2以及OB与OC的夹角θ3则有

(2)

投影中心与3个控制点间距离分别为L1、L2和L3,根据角锥体原理同样有:

(3)

由式(1)～式(3)可以迭代获取Li(i=1,2,3)的准确数值,需要注意的是,以上方程组是二次的,所以可能存在两个解,需要采取适当的措施使Li(i=1,2,3)的结果满足真实的边长长短关系[11],在此不再赘述。

依Li的数值,可以求解出3个控制点在拼接相机坐标系下的空间坐标

(4)

根据3个控制点的在相机坐标系下的坐标值[11],求出拼接相机坐标系同全局坐标系的转换矩阵Mc。

2.3 由投影系统视觉传感器坐标系到拼接相机坐标系的转换

投影仪投射带有标记点图样的图像,由投影测量系统的CCD相机采集,通过图像处理提取标记点中心的像面坐标,再通过已建立的投影系统测量模型转换,即可得到投射在被测物表面的标记点在投影系统传感器坐标系下的坐标(Xs,Ys,Zs)。

任取3个标记点,在得到投射标记点在投影系统传感器坐标系下的坐标后,可以求得它们之间的距离关系,之后再利用2.2的方法,可以求解所有标记点在拼接相机坐标系下的坐标(Xc,Yc,Zc)。则有

(5)

R为3(3正交单位矩阵,称为坐标旋转矩阵,T=[ΔX,ΔY,ΔZ]T为三维平移矩阵,m为尺度因子。

常用的布尔莎(Bursa)模型在求解过程中采用了迈克劳林级数展开作了相关的近似处理,所以只适合旋转角为小角度的情况。本系统中在不确定以上两个坐标系旋转角度的情况下,对R矩阵不做近似处理,即R矩阵可写为:

则式(5)可以转化为:

(6)

式(6)中x=[ΔXΔYΔZma1ma2ma3mb1mb2mb3mc1mc2mc3]T,此式即为三维任意旋转角度坐标转换的基本模型,关键在求解该模型中的12个待估参数。

式(6)可以转化为矩阵方程l=Bx的形式,改写为误差方程的形式为:

V=Bx-l

(7)

由于R为正交矩阵,即RRT=RTR=E,所以待估参数满足以下条件:

(8)

如果只有3个观测点,利用式(7)和式(8)可以迭代求解[12],但是为了提高转换精度,通常会增加观测点,在这种情况下则用最小二乘法求解超定方程组。

根据最小二乘的思想,在观测方程l=Bx中,观测向量l中存在误差V,此时可以用整体最小二乘法求解出参数x的最优值。在最小二乘法中,考虑的是矩阵方程l+V=Bx,并且要满足x的取值满足残差VTV的值达到最小,即VTV=min(x)。具体的计算过程中,会将式(6)展开分解为三组方程组[13],分别为:

(9)

(10)

(11)

以上3个方程组都可以写成矩阵方程l′=B′x′的形式,可以看出式(9)、式(10)、式(11)都满足最小二乘回归模型,之后再根据超定方程组求解的方法求解最小二乘解,通过以上3个方程组的解,可以算出12个待估参数。

3 具体方案的设计

3.1 投射标记点方案

DLP数字投影仪在其投射的范围内可以投射上位机指定的图像,所以需要考虑选取的图案能够使测量精度达到最佳;同时考虑到被测物体表面可能存在形状突变或形状变化较大的地方,在这些地方如果投射圆形标记点可能会被调制为一些不可预知的形状;最后投射的标记点要具有识别特征,便于后期传感器相机与全局相机进行标记点匹配。综合考虑以上因素,本方案选取的投射图样是均匀分布的一系列排列紧密编码同心圆环形标记点。

首先,当有大量标记点投射在物体表面时,可以选取一些形变较小的标记点用来图像拼接,这也就剔除了那些形状变化较大标记点;同时当投影系统遮挡拼接相机部分视角的情况下,保证拼接相机可以拍摄到足够多的标记点用来解算坐标系转换关系。再有,我们采用的编码方式是圆形编码点,如图4所示,这样通过不同编码,可以辅助两个相机拍到编码点的匹配。

图4 一个完整的8位编码同心圆环标记点

最后,当标记点投射在被测物表面较为平缓的位置时,标记点的形状可以看作是同中心椭圆,拼接相机和传感器相机分别拍摄得到物体表面的标记点图像。为了保证传感器相机与全局拼接相机图像中提取的标记点中心对应的是空间中的一个点,准确解算传感器坐标系到拼接相机坐标系的转换关系,可以采用直接最小二乘算法[14]拟合拍摄到的图像的中心。而采取同心圆标记点的目的是使用修正算法补偿透视投影几何变换中的圆心偏差[15]。

3.2 坐标系转换关系的优化求解

在求解转换关系Mc和Ms-c的过程中,采用了单幅图像的方法,只需3个标记点,在已知3个标记点之间的距离关系后,即可求出这3个标记点在拼接相机坐标系下的坐标,避免了交汇定向方式中匹配的问题,拼接算法效率较高,同时拼接相机在空间中拍摄的位置自由,能够克服投影系统传感器遮挡的问题。但共面三点在深度方向上无法提供有力的约束,只能依靠拼接相机标定精度,特别是深度方向的误差不容忽视[16],因此必须采取必要的修正措施。

考虑到拼接相机的大视场、高分辨率特征,求解过程充分利用拼接相机拍到的全局控制点和投射标记点建立光束平差模型。以全局控制点为例,由相机成像模型可知,任一空间点图像坐标与三维坐标满足如下关系式[17]:

(12)

式(12)中:(x,y)表示实际像点坐标,(X,Y,Z)表示全局控制点在全局坐标系下的三维坐标,(x0,y0)是主点位置坐标,(Δx,Δy)表示像点坐标的畸变量,是拼接相机坐标系相对全局坐标系的旋转矩阵因子和平移矩阵因子。设拼接相机拍到的全局控制点的个数为n,联立成像光线方程,得到如下方程组:

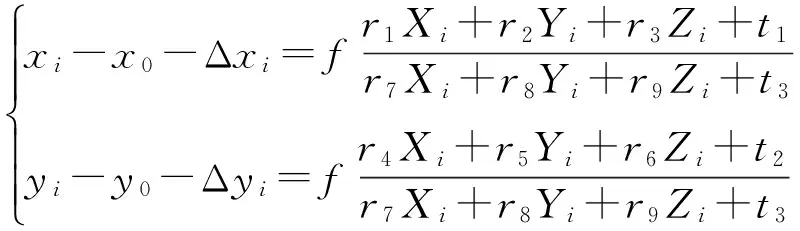
(13)

式(13)中,n个全局控制点坐标在全局坐标系下的三维坐标已知,相机的内参也已精确标定,未知量仅为r1-r9,t1-t3,实际上旋转矩阵因子r1-r9满足如式(8)正交关系,所以当有3个以上全局控制点被拍到时,利用非线性优化方法进行迭代求解,而迭代初值采用3.2节的方法获得,具体迭代过程采用牛顿迭代法。通过以上方法可以有效减小误差,在一些对于精度要求更高的应用场合,可以通过拼接相机在不同位姿拍摄多张图像,利用单相机多摄站空间交汇模型进行求解坐标系转换关系[16,18]。

4 基于投影标记点和全局控制点的拼接实验

实验中用到的DLP投影仪选择了Ti公司的DLP LightCrafter,此款投影装置可以由上位机控制选择投射的模式与图像;相机采用了JAI公司的型号为CV-M4+CL工业CCD相机,这款相机最大帧率可达24 frame/s,满足了测量速度的要求,传感器工作距离约300 mm,投影仪与相机之间距离约250 mm,视场范围约200 mm×120 mm;拼接相机采用Megaplus6.3i(3 066像素×2 048像素)CCD相机,满足了高分辨率的要求,同时安装Nikon 28 mm广角镜头以最大限度地采集到视场中的全局控制点和投射标记点,使用过程中将相机固定在三脚架上,投影系统传感器每到一个位置,可以适当移动三脚架的位置,以便于拼接相机拍摄投影标记点和全局控制点。

首先验证拼接精度,采取以下实验设计:在空间中放置一块带标记点的平面靶标,视觉传感器在第一个位置对平面靶标进行测量;之后平面靶标位置不动,视觉传感器移动到第2个位置进行测量,即视觉传感器坐标系在前后两次空间位置发生了变化,而平面靶标的空间位置是保持不变的。在两次测量公共视场范围内的标定靶标上选取40个特征点,理论上两次测量的靶标上特征点三维坐标应相等,依此评价拼接精度。在视觉传感器前后两个位置,依据本文提出的坐标转换模型可以分别得到公共视场范围内40个点在全局坐标系中的三维坐标,然后计算拼接后两次平面靶标上40个特征点三维坐标在X、Y、Z3个方向上的差值,最后分别将40组差值的均方根值求出,得到X、Y、Z3个方向上的RMS误差分别为:0.056 mm、0.023 mm、0.165 mm,图5为两次测量中得到的40个点拼接后在全局坐标系中的坐标,图中‘○’为第一个位置所测点,‘+’为第2个位置所测点。

图5 两次测量公共点对比图

之后考虑到测量中形貌拼接过程坐标系转换对于整个系统精度的影响,本文设计了测量系统绝对精度验证实验:在不同的几块传感器投影范围内贴上a1,a2,…,a1010个人工标记点,通过坐标系转换模型将这10个点在全局坐标系下的坐标求出,这10个坐标值是测量值。再采用V-stars测量系统测量这10个点的空间坐标,以同样3个全局控制点建立坐标系,可以近似得到这10个点在全局坐标系下的真实坐标值(V-stars系统在10 m范围内测量精度可以达到0.08 mm)。两组数据比对结果如表1所示,实验结果显示10个点距离误差平均值为0.33 mm,表明依据本文提出的拼接方案搭建的测量系统具有较高的测量精度。

表1 拼接数据误差分析结果(单位:mm)

5 结论

本文给出了基于光栅投影精密测量的三维形貌拼接实现方案,使精度较高、技术成熟的光栅投影测量方法可以应用于尺寸较大的三维形貌测量,同现有的一系列方案相比,此方案优势明显:投射标记点不影响被测形貌自身特征,且操作简洁、效率高;对于投影系统视觉传感器位姿没有限制;从原理上克服了基于相邻图像重叠拼接中的误差累积问题。从实验结果来看,本文提出的拼接方法在X,Y,Z坐标的RMS误差分别为:0.056 mm、0.023 mm、0.165 mm,测量系统的绝对精度为:0.33 mm,精度较高,可以应用于一般精度要求,为大型面形的三维视觉测量提供了一种有效方法。

[1] 吴艳.结构光投影三维测量方法的研究[D].西安:西安建筑科技大学,2012.

[2]张洪涛,段发阶,王学影,等.多传感器视觉测量系统坐标统一技术研究[J].传感技术学报,2006,19(4):1301-1304.

[3]龙玺,钟约先.结构光三维扫描测量的三维拼接技术[J].清华大学学报(自然科学版),2002,42(4):477-480.

[4]马扬飚,钟约先,郑聆,等.三维数据拼接中编码标志点的设计与检测[J].清华大学学报(自然科学版),2006,46(2):169-171.

[5]张效栋,孙长库.新型简易三维数字化全貌测量系统[J].传感技术学报,2008,21(10):1798-1803.

[6]Member Paul J Besl.A Method for Registration of 3-D Shapes[J].IEEE Transaction on Pattern Analysis and Machine Intelligence,1992,14(2):239-256.

[7]张广军,孙军华,魏振忠,等.基于单经纬仪的视觉测量三维数据拼接方法[J].仪器仪表学报,2007,28(3):441-445.

[8]李喆,丁振良,袁峰.基于共面点的多视觉测量系统的全局标定[J].光学精密工程,2008(3):467-472.

[9]Huang Shujun,Zhang Zonghua,Zhao Yan.3D Fingerprint Imaging System Based on Full-Field Fringe Projection Profilometry[J].Optics and Lasers in Engineering,2014,52(1):123-130.

[10]张一平,龚志辉,王勃.基于大倾角的角锥体空间后方交会研究[J].测绘工程,2012,21(2):17-20.

[11]邾继贵,王大为,任同群,等.基于单次成像的三维形貌拼接技术[J].机械工程学报,2007,43(6):186-189.

[12]王保丰,徐宁,余春平,等.两种空间直角坐标系转换参数初值快速计算的方法[J].宇航计测技术,2007,27(4):20-24.

[13]许超钤,姚宜斌,熊思婷,等.三维任意旋转角度坐标转换的整体最小二乘回归解法[J].测绘信息与工程,2010(5):46-48.

[14]Fitzgibbon A,Pilu M,Fisher R B.Direct Least Square Fitting of Ellipses[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1999,21(5):476-480.

[15]达飞鹏,盖绍彦.光栅投影三维测量[M].科学出版社,2011:1-2.

[16]任同群,邾继贵,李艳军,等.形貌测量中立体图像拼接的关键技术[J].机械工程学报,2008,44(5):137-141.

[17]郭磊.移动视觉精密测量关键技术研究[D].天津:天津大学,2011.

[18]黄桂平,叶声华,李广云.数字近景工业摄影测量关键技术研究与应用[D].天津:天津大学,2005.

刘常杰(1973-),男,山东威海人,博士,副教授,硕士生导师,主要从事激光及光电测试技术方面研究;

刘洋(1989-),男,天津人,硕士在读,主要研究工作是光栅投影三维精密测量。

TheResearchof3DMorphologySplicingTechniquesofGratingProjectionMeasuringSystem*

LIUChangjie*,LIUYang,LIUMiao,LIBin

(State Key Laboratory of Precision Measuring Technology and Instruments,Tianjin University,Tianjin 300072,China)

To solve the morphology measurement of objects which are large in size or complex in surface,a 3D morphology splicing scheme based on projection markers and global controlling points is proposed.The scheme makes full use of the advantages of grating projection measuring system.Using splicing camera coordinate system as the intermediary,multi-view point cloud coordinates of measured surfaces in the projection system vision sensor coordinate system are converted to the global coordinate system.Measurement data which are measured by the projection system vision sensor in different positions and different angles are unified into the global coordinate system so that the morphology splicing can be accomplished.This scheme avoids pasting the artificial markers and maintains the original morphology of the surface of the measured objects.Measuring efficiency is improved and the error accumulation problem based on the overlap splicing of adjacent images is overcome.The method of this scheme is simple and practical.The accuracy can also meet the requirements.The experimental results show that the splicing RMS errors ofX,Y,Zcoordinate are 0.056 mm,0.023 mm and 0.165 mm.The absolute error of the measurement system is 0.33 mm.

grating projection measurement;morphology splicing;projection markers;the global control points

项目来源:国家“863”计划项目(2012AA041205)

2014-04-09修改日期:2014-06-03

10.3969/j.issn.1004-1699.2014.07.004

TP391;TH741

:A

:1004-1699(2014)07-0870-06